Property Specification Language on:
[Wikipedia]
[Google]
[Amazon]
Property Specification Language (PSL) is a temporal logic extending linear temporal logic with a range of operators for both ease of expression and enhancement of expressive power. PSL makes an extensive use of
always (request -> eventually! grant)
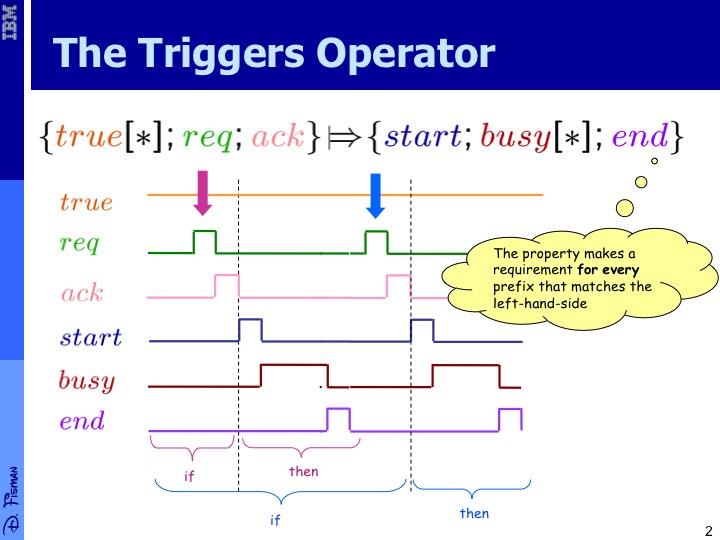
The property "every that is immediately followed by an signal, should be followed by a complete , where a complete data transfer is a sequence starting with signal , ending with signal in which holds at the meantime" can be expressed by the PSL formula:
(true req; ack) , => (start; busy end)
A trace satisfying this formula is given in the figure on the right.
 PSL's temporal operators can be roughly classified into ''LTL-style'' operators and ''regular-expression-style'' operators. Many PSL operators come in two versions, a strong version, indicated by an exclamation mark suffix ( ), and a weak version. The ''strong version'' makes eventuality requirements (i.e. require that something will hold in the future), while the ''weak version'' does not. An ''underscore suffix'' ( ) is used to differentiate ''inclusive'' vs. ''non-inclusive'' requirements. The and suffixes are used to denote ''universal'' (all) vs. ''existential'' (exists) requirements. Exact time windows are denoted by and flexible by .
PSL's temporal operators can be roughly classified into ''LTL-style'' operators and ''regular-expression-style'' operators. Many PSL operators come in two versions, a strong version, indicated by an exclamation mark suffix ( ), and a weak version. The ''strong version'' makes eventuality requirements (i.e. require that something will hold in the future), while the ''weak version'' does not. An ''underscore suffix'' ( ) is used to differentiate ''inclusive'' vs. ''non-inclusive'' requirements. The and suffixes are used to denote ''universal'' (all) vs. ''existential'' (exists) requirements. Exact time windows are denoted by and flexible by .
 The regular expressions of PSL have the common operators for concatenation (), Kleene-closure (), and union (), as well as operator for fusion (), intersection () and a weaker version (), and many variations for consecutive counting and in-consecutive counting e.g. and .
The trigger operator comes in several variations, shown in the table below.
Here and are PSL-regular expressions, and is a PSL formula.
Operators for concatenation, fusion, union, intersection and their variations are shown in the table below.
Here and are PSL regular expressions.
Operators for consecutive repetitions are shown in the table below.
Here is a PSL regular expression.
Operators for non-consecutive repetitions are shown in the table below.
Here is any PSL Boolean expression.
The regular expressions of PSL have the common operators for concatenation (), Kleene-closure (), and union (), as well as operator for fusion (), intersection () and a weaker version (), and many variations for consecutive counting and in-consecutive counting e.g. and .
The trigger operator comes in several variations, shown in the table below.
Here and are PSL-regular expressions, and is a PSL formula.
Operators for concatenation, fusion, union, intersection and their variations are shown in the table below.
Here and are PSL regular expressions.
Operators for consecutive repetitions are shown in the table below.
Here is a PSL regular expression.
Operators for non-consecutive repetitions are shown in the table below.
Here is any PSL Boolean expression.
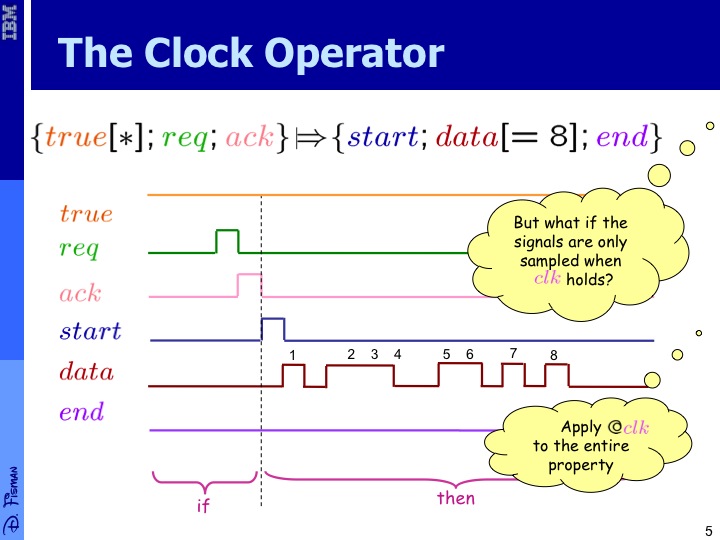 The first property states that "every that is immediately followed by an signal, should be followed by a complete , where a complete data transfer is a sequence starting with signal , ending with signal in which should hold at least 8 times:
The first property states that "every that is immediately followed by an signal, should be followed by a complete , where a complete data transfer is a sequence starting with signal , ending with signal in which should hold at least 8 times:
(true req; ack) , => (start; data 8 end)
But sometimes it is desired to consider only the cases where the above signals occur on a cycle where is high.
This is depicted in the second figure in which although the formula
((true req; ack) , => (start; data 3 end)) @ clk
uses and is consecutive repetition, the matching trace has 3 non-consecutive time points where holds, but when considering only the time points where holds, the time points where hold become consecutive.
 The semantics of formulas with nested @ is a little subtle. The interested reader is referred to
The semantics of formulas with nested @ is a little subtle. The interested reader is referred to
IEEE 1850 working group
Accellera
Property Specification Language Tutorial
Designers guide to PSL
* ttps://www.springer.com/engineering/circuits+%26+systems/book/978-0-387-35313-5 A Practical Introduction to PSL Cindy Eisner and Dana Fisman {{IEEE standards Hardware verification languages Formal specification languages IEEE DASC standards IEC standards
regular expressions
A regular expression (shortened as regex or regexp), sometimes referred to as rational expression, is a sequence of character (computing), characters that specifies a pattern matching, match pattern in string (computer science), text. Usually ...
and syntactic sugaring. It is widely used in the hardware design and verification industry, where formal verification
In the context of hardware and software systems, formal verification is the act of proving or disproving the correctness of a system with respect to a certain formal specification or property, using formal methods of mathematics.
Formal ver ...
tools (such as model checking
In computer science, model checking or property checking is a method for checking whether a finite-state model of a system meets a given specification (also known as correctness). This is typically associated with hardware or software syst ...
) and/or logic simulation
Logic simulation is the use of simulation software to predict the behavior of digital circuits and hardware description languages. Simulation can be performed at varying degrees of physical abstraction, such as at the transistor level, gate ...
tools are used to prove or refute that a given PSL formula holds on a given design.
PSL was initially developed by Accellera for specifying properties
Property is the ownership of land, resources, improvements or other tangible objects, or intellectual property.
Property may also refer to:
Philosophy and science
* Property (philosophy), in philosophy and logic, an abstraction characterizing an ...
or assertions about hardware designs. Since September 2004 the standardization on the language has been done in IEEE
The Institute of Electrical and Electronics Engineers (IEEE) is an American 501(c)(3) organization, 501(c)(3) public charity professional organization for electrical engineering, electronics engineering, and other related disciplines.
The IEEE ...
1850 working group. In September 2005, the IEEE 1850 Standard for Property Specification Language (PSL) was announced.
Syntax and semantics
PSL can express that if some scenario happens now, then another scenario should happen some time later. For instance, the property "a should always eventually be ed" can be expressed by the PSL formula: PSL's temporal operators can be roughly classified into ''LTL-style'' operators and ''regular-expression-style'' operators. Many PSL operators come in two versions, a strong version, indicated by an exclamation mark suffix ( ), and a weak version. The ''strong version'' makes eventuality requirements (i.e. require that something will hold in the future), while the ''weak version'' does not. An ''underscore suffix'' ( ) is used to differentiate ''inclusive'' vs. ''non-inclusive'' requirements. The and suffixes are used to denote ''universal'' (all) vs. ''existential'' (exists) requirements. Exact time windows are denoted by and flexible by .
PSL's temporal operators can be roughly classified into ''LTL-style'' operators and ''regular-expression-style'' operators. Many PSL operators come in two versions, a strong version, indicated by an exclamation mark suffix ( ), and a weak version. The ''strong version'' makes eventuality requirements (i.e. require that something will hold in the future), while the ''weak version'' does not. An ''underscore suffix'' ( ) is used to differentiate ''inclusive'' vs. ''non-inclusive'' requirements. The and suffixes are used to denote ''universal'' (all) vs. ''existential'' (exists) requirements. Exact time windows are denoted by and flexible by .
SERE-style operators
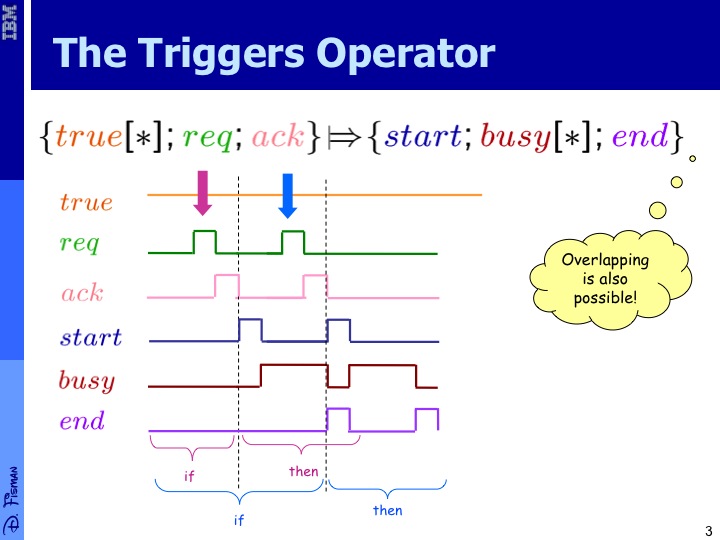
The most commonly used PSL operator is the "suffix-implication" operator (also known as the "triggers" operator), which is denoted by . Its left operand is a PSL regular expression and its right operand is any PSL formula (be it in LTL style or regular expression style). The semantics of is that on every time point i such that the sequence of time points up to i constitute a match to the regular expression r, the path from i+1 should satisfy the property p. This is exemplified in the figures on the right.

 The regular expressions of PSL have the common operators for concatenation (), Kleene-closure (), and union (), as well as operator for fusion (), intersection () and a weaker version (), and many variations for consecutive counting and in-consecutive counting e.g. and .
The trigger operator comes in several variations, shown in the table below.
Here and are PSL-regular expressions, and is a PSL formula.
Operators for concatenation, fusion, union, intersection and their variations are shown in the table below.
Here and are PSL regular expressions.
Operators for consecutive repetitions are shown in the table below.
Here is a PSL regular expression.
Operators for non-consecutive repetitions are shown in the table below.
Here is any PSL Boolean expression.
The regular expressions of PSL have the common operators for concatenation (), Kleene-closure (), and union (), as well as operator for fusion (), intersection () and a weaker version (), and many variations for consecutive counting and in-consecutive counting e.g. and .
The trigger operator comes in several variations, shown in the table below.
Here and are PSL-regular expressions, and is a PSL formula.
Operators for concatenation, fusion, union, intersection and their variations are shown in the table below.
Here and are PSL regular expressions.
Operators for consecutive repetitions are shown in the table below.
Here is a PSL regular expression.
Operators for non-consecutive repetitions are shown in the table below.
Here is any PSL Boolean expression.
LTL-style operators
Below is a sample of some LTL-style operators of PSL. Here and are any PSL formulas.Sampling operator
Sometimes it is desirable to change the definition of the ''next time-point'', for instance in multiply-clocked designs, or when a higher level of abstraction is desired. The ''sampling operator'' (also known as the ''clock operator''), denoted , is used for this purpose. The formula where is a PSL formula and a PSL Boolean expressions holds on a given path if on that path projected on the cycles in which holds, as exemplified in the figures to the right. The first property states that "every that is immediately followed by an signal, should be followed by a complete , where a complete data transfer is a sequence starting with signal , ending with signal in which should hold at least 8 times:
The first property states that "every that is immediately followed by an signal, should be followed by a complete , where a complete data transfer is a sequence starting with signal , ending with signal in which should hold at least 8 times:
 The semantics of formulas with nested @ is a little subtle. The interested reader is referred to
The semantics of formulas with nested @ is a little subtle. The interested reader is referred to
Abort operators
PSL has several operators to deal with truncated paths (finite paths that may correspond to a prefix of the computation). Truncated paths occur in bounded-model checking, due to resets and in many other scenarios. The abort operators, specify how eventualities should be dealt with when a path has been truncated. They rely on the truncated semantics proposed in Here is any PSL formula and is any PSL Boolean expression.Expressive power
PSL subsumes the temporal logic LTL and extends its expressive power to that of the omega-regular languages. The augmentation in expressive power, compared to that of LTL, which has the expressive power of the star-free ω-regular expressions, can be attributed to the ''suffix implication'', also known as the ''triggers'' operator, denoted ", ->". The formula ''r , -> f'' where ''r'' is a regular expression and ''f'' is a temporal logic formula holds on a computation ''w'' if any prefix of ''w'' matching ''r'' has a continuation satisfying ''f''. Other non-LTL operators of PSL are the ''@'' operator, for specifying multiply-clocked designs, the ''abort'' operators, for dealing with hardware resets, and ''local variables'' for succinctness.Layers
PSL is defined in 4 layers: the ''Boolean layer'', the ''temporal layer'', the ''modeling layer'' and the ''verification layer''. *The ''Boolean layer'' is used for describing a current state of the design and is phrased using one of the above-mentioned HDLs. *The ''temporal layer'' consists of the temporal operators used to describe scenarios that span over time (possibly over an unbounded number of time units). *The ''modeling layer'' can be used to describe auxiliary state machines in a procedural manner. *The ''verification layer'' consists of directives to a verification tool (for instance to ''assert'' that a given property is correct or to ''assume'' that a certain set of properties is correct when verifying another set of properties).Language compatibility
Property Specification Language can be used with multiple electronic system design languages (HDLs) such as: *VHDL
VHDL (Very High Speed Integrated Circuit Program, VHSIC Hardware Description Language) is a hardware description language that can model the behavior and structure of Digital electronics, digital systems at multiple levels of abstraction, ran ...
(IEEE 1076)
* Verilog
Verilog, standardized as IEEE 1364, is a hardware description language (HDL) used to model electronic systems. It is most commonly used in the design and verification of digital circuits, with the highest level of abstraction being at the re ...
(IEEE 1364)
* SystemVerilog (IEEE 1800)
* SystemC (IEEE 1666) by Open SystemC Initiative (OSCI).
When PSL is used in conjunction with one of the above HDLs, its Boolean layer uses the operators of the respective HDL.
References
* **IEC 62531:2007 * **IEC 62531:2012 * *External links
IEEE 1850 working group
Accellera
Property Specification Language Tutorial
Designers guide to PSL
Books on PSL
* ttps://www.springer.com/engineering/circuits+%26+systems/book/978-0-387-35313-5 A Practical Introduction to PSL Cindy Eisner and Dana Fisman {{IEEE standards Hardware verification languages Formal specification languages IEEE DASC standards IEC standards