Pressure Prism on:
[Wikipedia]
[Google]
[Amazon]
A pressure prism is a way of visually describing the variation of
Hydrostatic pressure is the pressure exerted by a fluid at rest – for example, on the sides of a swimming pool, a glass of water or the bottom of the ocean. Its value at any given location within the fluid is the product of the fluid density (''ρ''), the depth (''d''), and the forces applied by gravity (''g'') plus any background pressures, such as atmospheric pressure.
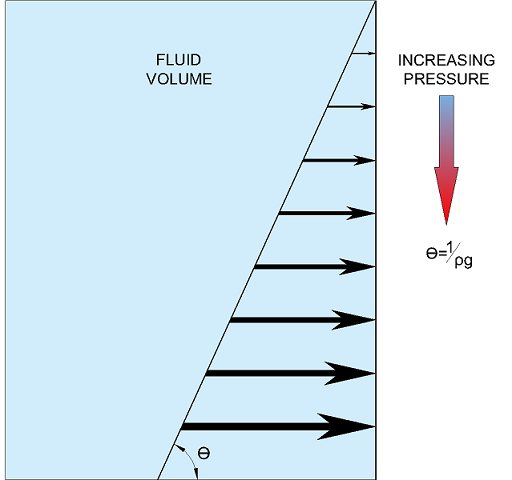
Hydrostatic pressure on surfaces surrounding (or within) fluid volumes can be represented by the ''pressure prism'', a useful visualization technique.
Hydrostatic pressure (''P'') increases linearly with depth. Generally it can be expressed by the relationship below, where the pressure at the top is zero and at the bottom is ''ρgH'', ''H'' being the total depth of the fluid volume.
''P'' = ''ρgd'', where ''P'' is the gauge pressure above atmospheric pressure
''ρ'' is the density of the fluid
''g'' is gravitational acceleration
''d'' is the target depth of the fluid
Variation of pressure with depth is shown in the first Figure above.
Further, the centre of pressure (''COP'') on the surrounding wall can be calculated by the following formula:
''HCOP'' = ''∫px'' x ''dx'' / ''∫px'' ''dx'', where ''px'' is the pressure at ''x'' distance from the bottom
With this formula we see the height of the ''COP'' for a plane surface is ''H/3'' from the bottom, as shown in Figure 2 (left).
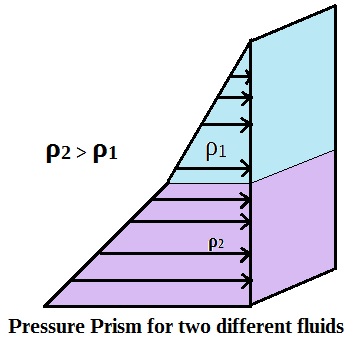
With two fluids of differing density in a volume, the slope of the pressure prism will not be constant over the depth. See Figure 3 (right).
The pressure prisms shown as examples pertain to situations where the surrounding surfaces are flat. Pressure prisms for fluid volumes with curved surfaces are more complex.
hydrostatic pressure
Hydrostatics is the branch of fluid mechanics that studies fluids at hydrostatic equilibrium and "the pressure in a fluid or exerted by a fluid on an immersed body". The word "hydrostatics" is sometimes used to refer specifically to water and o ...
within a volume of fluid. When variables of fluid density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be use ...
, depth, gravity
In physics, gravity (), also known as gravitation or a gravitational interaction, is a fundamental interaction, a mutual attraction between all massive particles. On Earth, gravity takes a slightly different meaning: the observed force b ...
, and other forces such as atmospheric pressure
Atmospheric pressure, also known as air pressure or barometric pressure (after the barometer), is the pressure within the atmosphere of Earth. The standard atmosphere (symbol: atm) is a unit of pressure defined as , which is equivalent to 1,013. ...
are charted, the resulting figure somewhat resembles a prism
PRISM is a code name for a program under which the United States National Security Agency (NSA) collects internet communications from various U.S. internet companies. The program is also known by the SIGAD . PRISM collects stored internet ...
.
Description
Hydrostatic pressure is the pressure exerted by a fluid at rest – for example, on the sides of a swimming pool, a glass of water or the bottom of the ocean. Its value at any given location within the fluid is the product of the fluid density (''ρ''), the depth (''d''), and the forces applied by gravity (''g'') plus any background pressures, such as atmospheric pressure.
Hydrostatic pressure on surfaces surrounding (or within) fluid volumes can be represented by the ''pressure prism'', a useful visualization technique.
Hydrostatic pressure (''P'') increases linearly with depth. Generally it can be expressed by the relationship below, where the pressure at the top is zero and at the bottom is ''ρgH'', ''H'' being the total depth of the fluid volume.
''P'' = ''ρgd'', where ''P'' is the gauge pressure above atmospheric pressure
''ρ'' is the density of the fluid
''g'' is gravitational acceleration
''d'' is the target depth of the fluid
Variation of pressure with depth is shown in the first Figure above.
Further, the centre of pressure (''COP'') on the surrounding wall can be calculated by the following formula:
''HCOP'' = ''∫px'' x ''dx'' / ''∫px'' ''dx'', where ''px'' is the pressure at ''x'' distance from the bottom
With this formula we see the height of the ''COP'' for a plane surface is ''H/3'' from the bottom, as shown in Figure 2 (left).
With two fluids of differing density in a volume, the slope of the pressure prism will not be constant over the depth. See Figure 3 (right).
The pressure prisms shown as examples pertain to situations where the surrounding surfaces are flat. Pressure prisms for fluid volumes with curved surfaces are more complex.
References
A Brief Introduction To Fluid Mechanics aperbackby Donald F. Young, Bruce R. Munson, Theodore H. Okiishi, Wade W. Huebsch {{Reflist Fluid statics