power method on:
[Wikipedia]
[Google]
[Amazon]
In
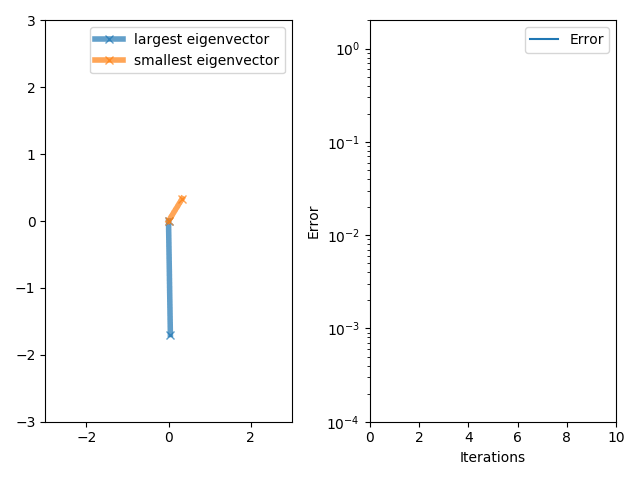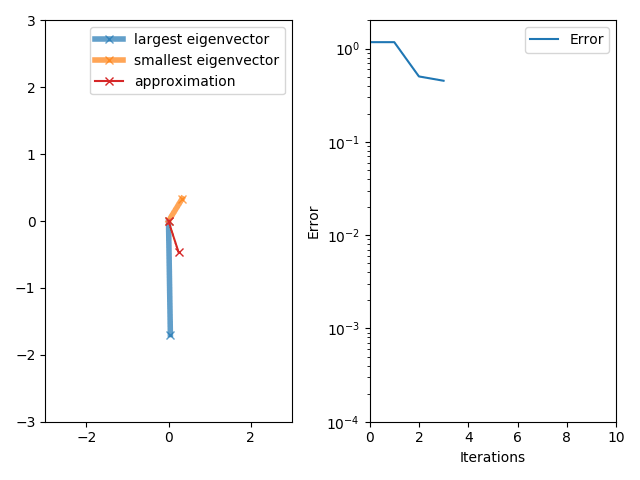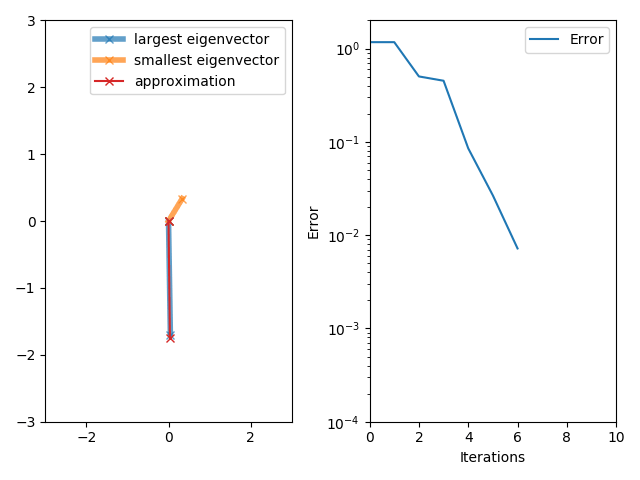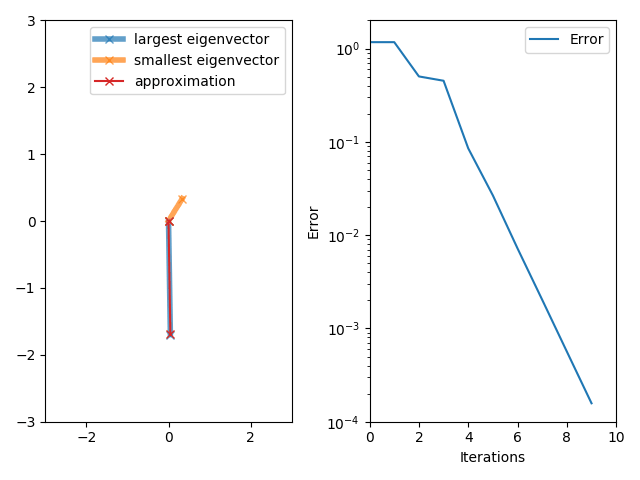 The power iteration algorithm starts with a vector , which may be an approximation to the dominant eigenvector or a random vector. The method is described by the
The power iteration algorithm starts with a vector , which may be an approximation to the dominant eigenvector or a random vector. The method is described by the
#!/usr/bin/env python3
import numpy as np
def power_iteration(A, num_iterations: int):
# Ideally choose a random vector
# To decrease the chance that our vector
# Is orthogonal to the eigenvector
b_k = np.random.rand(A.shape
for _ in range(num_iterations):
# calculate the matrix-by-vector product Ab
b_k1 = np.dot(A, b_k)
# calculate the norm
b_k1_norm = np.linalg.norm(b_k1)
# re normalize the vector
b_k = b_k1 / b_k1_norm
return b_k
power_iteration(np.array( 0.5, 0.5 .2, 0.8), 10)
The vector converges to an associated eigenvector. Ideally, one should use the
WTF: The who-to-follow system at Twitter
Proceedings of the 22nd international conference on World Wide Web The power iteration method is especially suitable for
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, power iteration (also known as the power method) is an eigenvalue algorithm: given a diagonalizable matrix
Matrix (: matrices or matrixes) or MATRIX may refer to:
Science and mathematics
* Matrix (mathematics), a rectangular array of numbers, symbols or expressions
* Matrix (logic), part of a formula in prenex normal form
* Matrix (biology), the m ...
, the algorithm will produce a number , which is the greatest (in absolute value) eigenvalue
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a ...
of , and a nonzero vector , which is a corresponding eigenvector
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by ...
of , that is, .
The algorithm is also known as the Von Mises iteration. Richard von Mises and H. Pollaczek-Geiringer,
''Praktische Verfahren der Gleichungsauflösung'', ZAMM - Zeitschrift für Angewandte Mathematik und Mechanik 9, 152-164 (1929).
Power iteration is a very simple algorithm, but it may converge slowly. The most time-consuming operation of the algorithm is the multiplication of matrix by a vector, so it is effective for a very large sparse matrix
In numerical analysis and scientific computing, a sparse matrix or sparse array is a matrix in which most of the elements are zero. There is no strict definition regarding the proportion of zero-value elements for a matrix to qualify as sparse ...
with appropriate implementation. The speed of convergence is like where is the number of iterations (see a later section). In words, convergence is exponential with base being the spectral gap
In mathematics, the spectral gap is the difference between the moduli of the two largest eigenvalues of a matrix or operator; alternately, it is sometimes taken as the smallest non-zero eigenvalue. Various theorems relate this difference to oth ...
.
The method
 The power iteration algorithm starts with a vector , which may be an approximation to the dominant eigenvector or a random vector. The method is described by the
The power iteration algorithm starts with a vector , which may be an approximation to the dominant eigenvector or a random vector. The method is described by the recurrence relation
In mathematics, a recurrence relation is an equation according to which the nth term of a sequence of numbers is equal to some combination of the previous terms. Often, only k previous terms of the sequence appear in the equation, for a parameter ...
:
So, at every iteration, the vector is multiplied by the matrix and normalized.
If we assume has an eigenvalue that is strictly greater in magnitude than its other eigenvalues and the starting vector has a nonzero component in the direction of an eigenvector associated with the dominant eigenvalue, then a subsequence converges to an eigenvector associated with the dominant eigenvalue.
Without the two assumptions above, the sequence does not necessarily converge. In this sequence,
: ,
where is an eigenvector associated with the dominant eigenvalue, and . The presence of the term implies that does not converge unless . Under the two assumptions listed above, the sequence defined by
:
converges to the dominant eigenvalue (with Rayleigh quotient
In mathematics, the Rayleigh quotient () for a given complex Hermitian matrix M and nonzero vector ''x'' is defined as:R(M,x) = .For real matrices and vectors, the condition of being Hermitian reduces to that of being symmetric, and the conjugat ...
).
One may compute this with the following algorithm (shown in Python with NumPy):
Rayleigh quotient
In mathematics, the Rayleigh quotient () for a given complex Hermitian matrix M and nonzero vector ''x'' is defined as:R(M,x) = .For real matrices and vectors, the condition of being Hermitian reduces to that of being symmetric, and the conjugat ...
in order to get the associated eigenvalue.
This algorithm is used to calculate the ''Google PageRank
PageRank (PR) is an algorithm used by Google Search to rank web pages in their search engine results. It is named after both the term "web page" and co-founder Larry Page. PageRank is a way of measuring the importance of website pages. Accordin ...
''.
The method can also be used to calculate the spectral radius
''Spectral'' is a 2016 Hungarian-American military science fiction action film co-written and directed by Nic Mathieu. Written with Ian Fried (screenwriter), Ian Fried & George Nolfi, the film stars James Badge Dale as DARPA research scientist Ma ...
(the eigenvalue with the largest magnitude, for a square matrix) by computing the Rayleigh quotient
:
Analysis
Let be decomposed into itsJordan canonical form
\begin
\lambda_1 1\hphantom\hphantom\\
\hphantom\lambda_1 1\hphantom\\
\hphantom\lambda_1\hphantom\\
\hphantom\lambda_2 1\hphantom\hphantom\\
\hphantom\hphantom\lambda_2\hphantom\\
\hphantom\lambda_3\hphantom\\
\hphantom\ddots\hphantom\\
...
: , where the first column of is an eigenvector of corresponding to the dominant eigenvalue . Since generically, the dominant eigenvalue of is unique, the first Jordan block of is the matrix where is the largest eigenvalue of ''A'' in magnitude. The starting vector can be written as a linear combination of the columns of ''V'':
:
By assumption, has a nonzero component in the direction of the dominant eigenvector, so .
The computationally useful recurrence relation
In mathematics, a recurrence relation is an equation according to which the nth term of a sequence of numbers is equal to some combination of the previous terms. Often, only k previous terms of the sequence appear in the equation, for a parameter ...
for can be rewritten as:
:
where the expression: is more amenable to the following analysis.
:
The expression above simplifies as
:
The limit follows from the fact that the eigenvalue of is less than 1 in magnitude, so
:
It follows that:
:
Using this fact, can be written in a form that emphasizes its relationship with when ''k'' is large:
:
where and as
The sequence is bounded, so it contains a convergent subsequence. Note that the eigenvector corresponding to the dominant eigenvalue is only unique up to a scalar, so although the sequence may not converge,
is nearly an eigenvector of ''A'' for large ''k''.
Alternatively, if ''A'' is diagonalizable, then the following proof yields the same result
Let λ1, λ2, ..., λ''m'' be the m eigenvalues (counted with multiplicity) of A and let ''v''1, ''v''2, ..., ''v''''m'' be the corresponding eigenvectors. Suppose that is the dominant eigenvalue, so that for .
The initial vector can be written:
:
If is chosen randomly (with uniform probability), then ''c''1 ≠ 0 with probability 1. Now,
:
On the other hand:
:
Therefore, converges to (a multiple of) the eigenvector . The convergence is geometric, with ratio
:
where denotes the second dominant eigenvalue. Thus, the method converges slowly if there is an eigenvalue close in magnitude to the dominant eigenvalue.
Applications
Although the power iteration method approximates only one eigenvalue of a matrix, it remains useful for certaincomputational problem
In theoretical computer science, a computational problem is one that asks for a solution in terms of an algorithm. For example, the problem of factoring
:"Given a positive integer ''n'', find a nontrivial prime factor of ''n''."
is a computati ...
s. For instance, Google
Google LLC (, ) is an American multinational corporation and technology company focusing on online advertising, search engine technology, cloud computing, computer software, quantum computing, e-commerce, consumer electronics, and artificial ...
uses it to calculate the PageRank
PageRank (PR) is an algorithm used by Google Search to rank web pages in their search engine results. It is named after both the term "web page" and co-founder Larry Page. PageRank is a way of measuring the importance of website pages. Accordin ...
of documents in their search engine, and Twitter
Twitter, officially known as X since 2023, is an American microblogging and social networking service. It is one of the world's largest social media platforms and one of the most-visited websites. Users can share short text messages, image ...
uses it to show users recommendations of whom to follow.Pankaj Gupta, Ashish Goel, Jimmy Lin, Aneesh Sharma, Dong Wang, and Reza Bosagh ZadeWTF: The who-to-follow system at Twitter
Proceedings of the 22nd international conference on World Wide Web The power iteration method is especially suitable for
sparse matrices
In numerical analysis and scientific computing, a sparse matrix or sparse array is a matrix (mathematics), matrix in which most of the elements are zero. There is no strict definition regarding the proportion of zero-value elements for a matrix ...
, such as the web matrix, or as the matrix-free method that does not require storing the coefficient matrix explicitly, but can instead access a function evaluating matrix-vector products . For non-symmetric matrices that are well-conditioned the power iteration method can outperform more complex Arnoldi iteration. For symmetric matrices, the power iteration method is rarely used, since its convergence speed can be easily increased without sacrificing the small cost per iteration; see, e.g., Lanczos iteration and LOBPCG.
Some of the more advanced eigenvalue algorithms can be understood as variations of the power iteration. For instance, the inverse iteration method applies power iteration to the matrix . Other algorithms look at the whole subspace generated by the vectors . This subspace is known as the Krylov subspace. It can be computed by Arnoldi iteration or Lanczos iteration.
Gram iteration is a super-linear and deterministic method to compute the largest eigenpair.
See also
* Rayleigh quotient iteration * Inverse iterationReferences
{{DEFAULTSORT:Power Iteration Numerical linear algebra Articles with example Python (programming language) code