Petri Net Theory

A Petri net, also known as a place/transition (PT) net, is one of several mathematical modeling languages for the description of distributed systems. It is a class of discrete event dynamic system. A Petri net is a directed bipartite graph that has two types of elements, places and transitions. Place elements are depicted as white circles and transition elements are depicted as rectangles.
A place can contain any number of tokens, depicted as black circles. A transition is enabled if all places connected to it as inputs contain at least one token. Some sources state that Petri nets were invented in August 1939 by Carl Adam Petri—at the age of 13—for the purpose of describing chemical processes.

Like industry standards such as UML activity diagrams, Business Process Model and Notation, and event-driven process chains, Petri nets offer a graphical notation for stepwise processes that include choice, iteration, and concurrent execution. Unlike these standards, Petri nets have an exact mathematical definition of their execution semantics, with a well-developed mathematical theory for process analysis.

Historical background

The German computer scientist Carl Adam Petri, for whom such structures are named, analyzed Petri nets extensively in his 1962 dissertation .

Petri net basics

A Petri net consists of ''places'', ''transitions'', and '' arcs''. Arcs run from a place to a transition or vice versa, never between places or between transitions. The places from which an arc runs to a transition are called the ''input places'' of the transition; the places to which arcs run from a transition are called the ''output places'' of the transition.

Graphically, places in a Petri net may contain a discrete number of marks called ''tokens''. Any distribution of tokens over the places will represent a configuration of the net called a ''marking''. In an abstract sense relating to a Petri net diagram, a transition of a Petri net may ''fire'' if it is ''enabled'', i.e. there are sufficient tokens in all of its input places; when the transition fires, it consumes the required input tokens, and creates tokens in its output places. A firing is atomic, i.e. a single non-interruptible step.

Unless an ''execution policy'' (e.g. a strict ordering of transitions, describing precedence) is defined, the execution of Petri nets is nondeterministic: when multiple transitions are enabled at the same time, they will fire in any order.

Since firing is nondeterministic, and multiple tokens may be present anywhere in the net (even in the same place), Petri nets are well suited for modeling the concurrent behavior of distributed systems.

Formal definition and basic terminology

Petri nets are state-transition systems that extend a class of nets called elementary nets.

Definition 1. A ''net'' is a tuple $N = (P, T, F)$ where
# $P$ and $T$ are disjoint finite sets of ''places'' and ''transitions'', respectively.
# $F \subseteq (P \times T) \cup (T \times P)$ is a set of (directed) ''arcs'' (or flow relations).

Definition 2. Given a net ''N'' = (''P'', ''T'', ''F''), a ''configuration'' is a set ''C'' so that ''C'' ⊆ ''P''.

Definition 3. An ''elementary net'' is a net of the form ''EN'' = (''N'', ''C'') where
# ''N'' = (''P'', ''T'', ''F'') is a net.
# ''C'' is such that ''C'' ⊆ ''P'' is a ''configuration''.

Definition 4. A ''Petri net'' is a net of the form ''PN'' = (''N'', ''M'', ''W''), which extends the elementary net so that
# ''N'' = (''P'', ''T'', ''F'') is a net.
# ''M'' : ''P'' → ''Z'' is a place multiset, where ''Z'' is a countable set. ''M'' extends the concept of ''configuration'' and is commonly described with reference to Petri net diagrams as a ''marking''.
# ''W'' : ''F'' → ''Z'' is an arc multiset, so that the count (or weight) for each arc is a measure of the arc ''multiplicity''.

If a Petri net is equivalent to an elementary net, then ''Z'' can be the countable set and those elements in ''P'' that map to 1 under ''M'' form a configuration. Similarly, if a Petri net is not an elementary net, then the multiset ''M'' can be interpreted as representing a non-singleton set of configurations. In this respect, ''M'' extends the concept of configuration for elementary nets to Petri nets.

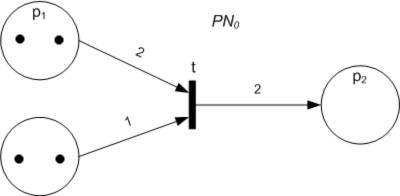
In the diagram of a Petri net (see top figure right), places are conventionally depicted with circles, transitions with long narrow rectangles and arcs as one-way arrows that show connections of places to transitions or transitions to places. If the diagram were of an elementary net, then those places in a configuration would be conventionally depicted as circles, where each circle encompasses a single dot called a ''token''. In the given diagram of a Petri net (see right), the place circles may encompass more than one token to show the number of times a place appears in a configuration. The configuration of tokens distributed over an entire Petri net diagram is called a ''marking''.

In the top figure (see right), the place ''p''₁ is an input place of transition ''t''; whereas, the place ''p''₂ is an output place to the same transition. Let ''PN''₀ (top figure) be a Petri net with a marking configured ''M''₀, and ''PN''₁ (bottom figure) be a Petri net with a marking configured ''M''₁. The configuration of ''PN''₀ ''enables'' transition ''t'' through the property that all input places have sufficient number of tokens (shown in the figures as dots) "equal to or greater" than the multiplicities on their respective arcs to ''t''. Once and only once a transition is enabled will the transition fire. In this example, the ''firing'' of transition ''t'' generates a map that has the marking configured ''M''₁ in the image of ''M''₀ and results in Petri net ''PN''₁, seen in the bottom figure. In the diagram, the firing rule for a transition can be characterised by subtracting a number of tokens from its input places equal to the multiplicity of the respective input arcs and accumulating a new number of tokens at the output places equal to the multiplicity of the respective output arcs.

Remark 1. The precise meaning of "equal to or greater" will depend on the precise algebraic properties of addition being applied on ''Z'' in the firing rule, where subtle variations on the algebraic properties can lead to other classes of Petri nets; for example, algebraic Petri nets.

The following formal definition is loosely based on . Many alternative definitions exist.

Syntax

A Petri net graph (called ''Petri net'' by some, but see below) is a 3-tuple $(S,T,W)$, where
* ''S'' is a finite set of ''places''
* ''T'' is a finite set of ''transitions''
* ''S'' and ''T'' are disjoint

HOME


Content is Copyleft
Website design, code, and AI is Copyrighted (c) 2014-2017 by Stephen Payne


Consider donating to Wikimedia



As an Amazon Associate I earn from qualifying purchases