Octonion

In mathematics, the octonions are a normed division algebra over the real numbers, a kind of hypercomplex number system. The octonions are usually represented by the capital letter O, using boldface or blackboard bold $\mathbb O$. Octonions have eight dimensions; twice the number of dimensions of the quaternions, of which they are an extension. They are noncommutative and nonassociative, but satisfy a weaker form of associativity; namely, they are alternative. They are also power associative.

Octonions are not as well known as the quaternions and complex numbers, which are much more widely studied and used. Octonions are related to exceptional structures in mathematics, among them the exceptional Lie groups. Octonions have applications in fields such as string theory, special relativity and quantum logic. Applying the Cayley–Dickson construction to the octonions produces the sedenions.

History

The octonions were discovered in December 1843 by John T. Graves, inspired by his friend William Rowan Hamilton's discovery of quaternions. Shortly before Graves' discovery of octonions, Graves wrote in a letter addressed to Hamilton on October 26, 1843, "If with your alchemy you can make three pounds of gold, why should you stop there?"

Graves called his discovery "octaves", and mentioned them in a letter to Hamilton dated 26 December 1843. He first published his result slightly later than Arthur Cayley's article. The octonions were discovered independently by Cayley and are sometimes referred to as Cayley numbers or the Cayley algebra. Hamilton described the early history of Graves's discovery.

Definition

The octonions can be thought of as octets (or 8-tuples) of real numbers. Every octonion is a real linear combination of the unit octonions:

:$\bigl\\ ,$

where is the scalar or real element; it may be identified with the real number That is, every octonion can be written in the form
:$x = x_0 e_0 + x_1 e_1 + x_2 e_2 + x_3 e_3 + x_4 e_4 + x_5 e_5 + x_6 e_6 + x_7 e_7\ ,$
with real coefficients .

Cayley–Dickson construction

A more systematic way of defining the octonions is via the Cayley–Dickson construction. Applying the Cayley–Dickson construction to the quaternions produces the octonions, which can be expressed as $\mathbb=\mathcal(\mathbb,1)$.

Much as quaternions can be defined as pairs of complex numbers, the octonions can be defined as pairs of quaternions. Addition is defined pairwise. The product of two pairs of quaternions and is defined by
:$( a, b )( c, d ) = ( a c - d^b, da + bc^ )\ ,$
where denotes the conjugate of the quaternion . This definition is equivalent to the one given above when the eight unit octonions are identified with the pairs
:

Arithmetic and operations

Addition and subtraction

Addition and subtraction of octonions is done by adding and subtracting corresponding terms and hence their coefficients, like quaternions.

Multiplication

Multiplication of octonions is more complex. Multiplication is distributive over addition, so the product of two octonions can be calculated by summing the products of all the terms, again like quaternions. The product of each pair of terms can be given by multiplication of the coefficients and a multiplication table of the unit octonions, like this one (given both by Arthur Cayley in 1845 and John T. Graves in 1843):

Most off-diagonal elements of the table are antisymmetric, making it almost a skew-symmetric matrix except for the elements on the main diagonal, as well as the row and column for which is an operand.

The table can be summarized as follows:

: $e_\ell e_m = \begin e_m , & \text\ell = 0 \\ e_\ell , & \textm = 0 \\ - \delta_e_0 + \varepsilon _ e_n, & \text \end$

where is the Kronecker delta (equal to if , and for ), and is a completely antisymmetric tensor with value when and any even number of permutations of the indices, but for any odd permutations of the listed triples (e.g. $\ \varepsilon_ = +1\$ but $\ \varepsilon_ = \varepsilon_ = -1\ ,$ however, $\ \varepsilon_ = \varepsilon_ = +1\$ again). Whenever any two of the three indices are the same,

The above definition is not unique, however; it is only one of 480 possible definitions for octonion multiplication with . The others can be obtained by permuting and changing the signs of the non-scalar basis elements The 480 different algebras are isomorphic, and there is rarely a need to consider which particular multiplication rule is used.

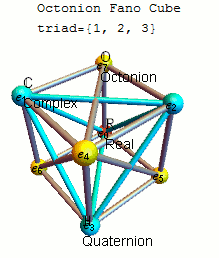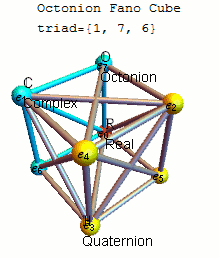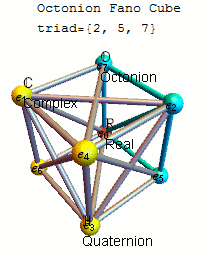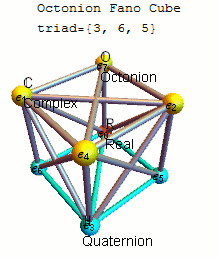
Each of these 480 definitions is invariant up to signs under some 7 cycle of the points and for each 7 cycle there are four definitions, differing by signs and reversal of order. A common choice is to use the definition invariant under the 7 cycle (1234567) with by using the triangular multiplication diagram, or Fano plane below that also shows the sorted list of based 7-cycle triads and its associated multiplication matrices in both and $\ \mathrm\$ format.
:

A variant of this sometimes used is to label the elements of the basis by the elements , 0, 1, 2, ..., 6, of the projective line over the finite field of order 7. The multiplication is then given by and , and all equations obtained from this one by adding a constant (modulo 7) to all subscripts: In other words using the seven triples These are the nonzero codewords of the quadratic residue code of length 7 over the Galois field of two elements, . There is a symmetry of order 7 given by adding a constant mod 7 to all subscripts, and also a symmetry of order 3 given by multiplying all subscripts by one of the quadratic residues 1, 2, 4 mod 7 .

: Available as , in particular

These seven triples can also be considered as the seven translates of the set of non-zero squares
forming a cyclic (7,3,1)- difference set in the finite field of seven elements.

The Fano plane shown above with $e_n$ and IJKL multiplication matrices also includes the geometric algebra basis with signature and is given in terms of the following 7 quaternionic triples (omitting the scalar identity element):
:

or alternatively:

:

in which the lower case items ' are vectors (e.g. , respectively) and the upper case ones = are bivectors (e.g. $\gamma_\gamma_$, respectively) and the Hodge star operator is the pseudo-scalar element. If the is forced to be equal to the identity, then the multiplication ceases to be associative, but the may be removed from the multiplication table resulting in an octonion multiplication table.

In keeping associative and thus not reducing the 4 dimensional geometric algebra to an octonion one, the whole multiplication table can be derived from the equation for . Consider the gamma matrices in the examples given above. The formula defining the fifth gamma matrix ($\gamma_$) shows that it is the of a four-dimensional geometric algebra of the gamma matrices.

Fano plane mnemonic

A convenient mnemonic for remembering the products of unit octonions is given by the diagram, which represents the multiplication table of Cayley and Graves.

This diagram with seven points and seven lines (the circle through 1, 2, and 3 is considered a line) is called the Fano plane. The lines are directional. The seven points correspond to the seven standard basis elements of \ \operatorname\mathcal\bigl \mathbb\ \bigr (see definition below). Each pair of distinct points lies on a unique line and each line runs through exactly three points.

Let be an ordered triple of points lying on a given line with the order specified by the direction of the arrow. Then multiplication is given by

: and

together with cyclic permutations. These rules together with

* is the multiplicative identity,
* $^2 = -1\$ for each point in the diagram

completely defines the multiplicative structure of the octonions. Each of the seven lines generates a subalgebra of $\ \mathbb\$ isomorphic to the quaternions .

Conjugate, norm, and inverse

The ''conjugate'' of an octonion

:$x = x_0\ e_0 + x_1\ e_1 + x_2\ e_2 + x_3\ e_3 + x_4\ e_4 + x_5\ e_5 + x_6\ e_6 + x_7\ e_7$

is given by

:$x^* = x_0\ e_0 - x_1\ e_1 - x_2\ e_2 - x_3\ e_3 - x_4\ e_4 - x_5\ e_5 - x_6\ e_6 - x_7\ e_7 ~.$
Conjugation is an involution of $\ \mathbb\$ and satisfies (note the change in order).

The ''real part'' of is given by

:$\frac = x_0\ e_0$

and the ''imaginary part'' (sometimes called the ''pure part'') by

:$\frac = x_1\ e_1 + x_2\ e_2 + x_3\ e_3 + x_4\ e_4 + x_5\ e_5 + x_6\ e_6 + x_7\ e_7 ~.$

The set of all purely imaginary octonions spans a 7  dimensional subspace of $\ \mathbb\ ,$ denoted \ \operatorname\mathcal\bigl \mathbb\ \bigr~.

Conjugation of octonions satisfies the equation

:$-6 x^* = x + (e_1x)e_1 + (e_2x)e_2 + (e_3x)e_3 + (e_4x)e_4 + (e_5x)e_5 + (e_6x)e_6 + (e_7x)e_7 ~.$

The product of an octonion with its conjugate, is always a nonnegative real number:

:$x^*x = x_0^2 + x_1^2 + x_2^2 + x_3^2 + x_4^2 + x_5^2 + x_6^2 + x_7^2 ~.$

Using this, the norm of an octonion is defined as

:$\, x\, = \sqrt ~.$

This norm agrees with the standard 8 dimensional Euclidean norm on .

The existence of a norm on $\ \mathbb\$ implies the existence of inverses for every nonzero element of $\ \mathbb ~.$ The inverse of which is the unique octonion satisfying is given by

:$x^ = \frac ~.$

Exponentiation and polar form

Any octonion can be decomposed into its real part and imaginary part:

$x=\mathfrak(x)+\mathfrak(x)$

also sometimes called scalar and vector parts.

We define the ''unit vector'' corresponding to as

$u=\frac$. It is a pure octonion of norm 1.

It can be proved that any non-zero octonion can be written as:

$o=\, o\, (\cos\theta+u\sin\theta)=\, o\, e^$

thus providing a polar form.

Properties

Octonionic multiplication is neither commutative:

: if , are distinct and non-zero,

nor associative:

: if , , are distinct, non-zero and .

The octonions do satisfy a weaker form of associativity: they are alternative. This means that the subalgebra generated by any two elements is associative. Actually, one can show that the subalgebra generated by any two elements of $\ \mathbb\$ is isomorphic to , , or , all of which are associative. Because of their non-associativity, octonions cannot be represented by a subalgebra of a matrix ring over , unlike the real numbers, complex numbers, and quaternions.

The octonions do retain one important property shared by , , and : the norm on $\ \mathbb\$ satisfies

:$\, x y \, = \, x \, \ \, y \, ~.$

This equation means that the octonions form a composition algebra. The higher-dimensional algebras defined by the Cayley–Dickson construction (starting with the sedenions) all fail to satisfy this property. They all have zero divisors.

Wider number systems exist which have a multiplicative modulus (for example, 16 dimensional conic sedenions). Their modulus is defined differently from their norm, and they also contain zero divisors.

As shown by Hurwitz, , , or , and $\ \mathbb\$ are the only normed division algebras over the real numbers. These four algebras also form the only alternative, finite-dimensional division algebras over the real numbers (up to an isomorphism).

Not being associative, the nonzero elements of $\ \mathbb\$ do not form a group. They do, however, form a loop, specifically a Moufang loop.

Commutator and cross product

The commutator of two octonions and is given by

:$$, y= xy - yx ~.

This is antisymmetric and imaginary. If it is considered only as a product on the imaginary subspace \ \operatorname\mathcal\bigl \mathbb\ \bigr it defines a product on that space, the seven-dimensional cross product, given by

:$x \times y = \tfrac\ (xy - yx) ~.$

Like the cross product in three dimensions this is a vector orthogonal to and with magnitude

:$\, x \times y\, = \, x\, \ \, y\, \ \sin \theta ~.$

But like the octonion product it is not uniquely defined. Instead there are many different cross products, each one dependent on the choice of octonion product.

Automorphisms

An automorphism, , of the octonions is an invertible linear transformation of $\ \mathbb\$ which satisfies

:$A(xy) = A(x)\ A(y) ~.$

The set of all automorphisms of $\ \mathbb\$ forms a group called The group is a simply connected, compact, real Lie group of dimension 14. This group is the smallest of the exceptional Lie groups and is isomorphic to the subgroup of that preserves any chosen particular vector in its 8 dimensional real spinor representation. The group is in turn a subgroup of the group of isotopies described below.

''See also'': – the automorphism group of the Fano plane.

Isotopies

An isotopy of an algebra is a triple of bijective linear maps , , such that if then . For this is the same as an automorphism. The isotopy group of an algebra is the group of all isotopies, which contains the group of automorphisms as a subgroup.

The isotopy group of the octonions is the group , with , , acting as the three 8 dimensional representations. The subgroup of elements where fixes the identity is the subgroup , and the subgroup where , , all fix the identity is the automorphism group

Matrix representation

Just as quaternions can be represented as matrices, octonions can be represented as tables of quaternions. Specifically, because any octonion can be defined a pair of quaternions, we represent the octonion $( q_0, q_1 )$ as:
$\begin q_0 & q_1 \\ -q_1^* & q_0^* \end$

Using a slightly modified (non-associative) quaternionic matrix multiplication:
$\begin \alpha_0 & \alpha_1 \\ \alpha_2 & \alpha_3 \end\circ\begin \beta_0 & \beta_1 \\ \beta_2 & \beta_3 \end=\begin \alpha_0\beta_0+\beta_2\alpha_1 & \beta_1\alpha_0+\alpha_1\beta_3\\ \beta_0\alpha_2+\alpha_3\beta_2 & \alpha_2\beta_1+\alpha_3\beta_3 \end$
we can translate octonion addition and multiplication to the respective operations on quaternionic matrices.

Applications

The octonions play a significant role in the classification and construction of other mathematical entities. For example, the exceptional Lie group is the automorphism group of the octonions, and the other exceptional Lie groups , , and can be understood as the isometries of certain projective planes defined using the octonions. The set of self-adjoint 3 × 3 octonionic matrices, equipped with a symmetrized matrix product, defines the Albert algebra. In discrete mathematics, the octonions provide an elementary derivation of the Leech lattice, and thus they are closely related to the sporadic simple groups.

Applications of the octonions to physics have largely been conjectural. For example, in the 1970s, attempts were made to understand quarks by way of an octonionic Hilbert space. It is known that the octonions, and the fact that only four normed division algebras can exist, relates to the spacetime dimensions in which supersymmetric quantum field theories can be constructed. Also, attempts have been made to obtain the Standard Model of elementary particle physics from octonionic constructions, for example using the "Dixon algebra" $\ \mathbb C \otimes \mathbb H \otimes \mathbb O ~.$

Octonions have also arisen in the study of black hole entropy, quantum information science, string theory, and image processing.

Octonions have been used in solutions to the hand eye calibration problem in robotics.

Deep octonion networks provide a means of efficient and compact expression in machine learning applications.

Integral octonions

There are several natural ways to choose an integral form of the octonions. The simplest is just to take the octonions whose coordinates are integers. This gives a nonassociative algebra over the integers called the Gravesian octonions. However it is not a maximal order (in the sense of ring theory); there are exactly seven maximal orders containing it. These seven maximal orders are all equivalent under automorphisms. The phrase "integral octonions" usually refers to a fixed choice of one of these seven orders.

These maximal orders were constructed by , Dickson and Bruck as follows. Label the eight basis vectors by the points of the projective line over the field with seven elements. First form the "Kirmse integers" : these consist of octonions whose coordinates are integers or half integers, and that are half integers (that is, halves of odd integers) on one of the 16 sets
:
of the extended quadratic residue code of length 8 over the field of two elements, given by , and its images under adding a constant modulo 7, and the complements of these eight sets. Then switch infinity and any one other coordinate; this operation creates a bijection of the Kirmse integers onto a different set, which is a maximal order. There are seven ways to do this, giving seven maximal orders, which are all equivalent under cyclic permutations of the seven coordinates 0123456. (Kirmse incorrectly claimed that the Kirmse integers also form a maximal order, so he thought there were eight maximal orders rather than seven, but as pointed out they are not closed under multiplication; this mistake occurs in several published papers.)

The Kirmse integers and the seven maximal orders are all isometric to the lattice rescaled by a factor of . In particular there are 240 elements of minimum nonzero norm 1 in each of these orders, forming a Moufang loop of order 240.

The integral octonions have a "division with remainder" property: given integral octonions and , we can find and with , where the remainder has norm less than that of .

In the integral octonions, all left ideals and right ideals are 2-sided ideals, and the only 2-sided ideals are the principal ideals where is a non-negative integer.

The integral octonions have a version of factorization into primes, though it is not straightforward to state because the octonions are not associative so the product of octonions depends on the order in which one does the products. The irreducible integral octonions are exactly those of prime norm, and every integral octonion can be written as a product of irreducible octonions. More precisely an integral octonion of norm can be written as a product of integral octonions of norms and .

The automorphism group of the integral octonions is the group of order 12,096, which has a simple subgroup of index 2 isomorphic to the unitary group . The isotopy group of the integral octonions is the perfect double cover of the group of rotations of the lattice.

See also

* G₂ manifold
* Octonion algebra
* Okubo algebra
* Spin(7) manifold
*
* Split-octonions
* Triality

Notes

References

*
*
* .
*
*
*
*
*
*
*
*

External links

* Koutsoukou-Argyraki, Angeliki
Octonions (Formal proof development in Isabelle/HOL, Archive of Formal Proofs)
*
*

{{Authority control

Composition algebras