N-connected space on:
[Wikipedia]
[Google]
[Amazon]
In
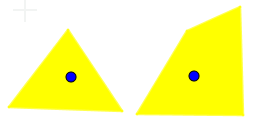
 * A 2-dimensional hole (a hole with a 1-dimensional boundary) is a circle (S1) in ''X'', that cannot be shrunk continuously to a point in ''X''. An example is shown on the figure at the right. The yellow region is the topological space ''X''; it is a pentagon with a triangle removed. The blue circle is a 1-dimensional sphere in ''X''. It cannot be shrunk continuously to a point in X; therefore; X has a 2-dimensional hole. Another example is the
* A 2-dimensional hole (a hole with a 1-dimensional boundary) is a circle (S1) in ''X'', that cannot be shrunk continuously to a point in ''X''. An example is shown on the figure at the right. The yellow region is the topological space ''X''; it is a pentagon with a triangle removed. The blue circle is a 1-dimensional sphere in ''X''. It cannot be shrunk continuously to a point in X; therefore; X has a 2-dimensional hole. Another example is the  * A 3-dimensional hole (a hole with a 2-dimensional boundary) is shown on the figure at the right. Here, ''X'' is a cube (yellow) with a ball removed (white). The 2-dimensional sphere (blue) cannot be continuously shrunk to a single point. ''X'' simply-connected but not 2-connected, so . The smallest dimension of a hole is 3, so .
* A 3-dimensional hole (a hole with a 2-dimensional boundary) is shown on the figure at the right. Here, ''X'' is a cube (yellow) with a ball removed (white). The 2-dimensional sphere (blue) cannot be continuously shrunk to a single point. ''X'' simply-connected but not 2-connected, so . The smallest dimension of a hole is 3, so .
 * For a 1-dimensional hole (a hole with a 0-dimensional boundary) we need to consider - the zero-dimensional sphere. What is a zero dimensional sphere? - For every integer ''d'', the sphere is the boundary of the (''d''+1)-dimensional ball . So is the boundary of , which is the segment ,1 Therefore, is the set of two disjoint points . A zero-dimensional sphere in ''X'' is just a set of two points in ''X''. If there is such a set, that cannot be continuously shrunk to a single point in ''X'' (or continuously extended to a segment in ''X''), this means that there is no path between the two points, that is, X is not
* For a 1-dimensional hole (a hole with a 0-dimensional boundary) we need to consider - the zero-dimensional sphere. What is a zero dimensional sphere? - For every integer ''d'', the sphere is the boundary of the (''d''+1)-dimensional ball . So is the boundary of , which is the segment ,1 Therefore, is the set of two disjoint points . A zero-dimensional sphere in ''X'' is just a set of two points in ''X''. If there is such a set, that cannot be continuously shrunk to a single point in ''X'' (or continuously extended to a segment in ''X''), this means that there is no path between the two points, that is, X is not
algebraic topology
Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify ...
, homotopical connectivity is a property describing a topological space based on the dimension of its holes. In general, low homotopical connectivity indicates that the space has at least one low-dimensional hole. The concept of ''n''-connectedness generalizes the concepts of path-connectedness and simple connectedness.
An equivalent definition of homotopical connectivity is based on the homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, denoted \pi_1(X), which records information about loops in a space. Intuitively, homot ...
s of the space. A space is ''n''-connected (or ''n''-simple connected) if its first ''n'' homotopy groups are trivial.
Homotopical connectivity is defined for maps, too. A map is ''n''-connected if it is an isomorphism
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word is ...
"up to dimension ''n,'' in homotopy
In topology, a branch of mathematics, two continuous functions from one topological space to another are called homotopic (from grc, ὁμός "same, similar" and "place") if one can be "continuously deformed" into the other, such a deform ...
".
Definition using holes
All definitions below consider a topological space ''X''. A hole in ''X'' is, informally, a thing that prevents some suitably-placed sphere from continuously shrinking to a point., Section 4.3 Equivalently, it is asphere
A sphere () is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. A sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the ...
that cannot be continuously extended to a ball
A ball is a round object (usually spherical, but can sometimes be ovoid) with several uses. It is used in ball games, where the play of the game follows the state of the ball as it is hit, kicked or thrown by players. Balls can also be used fo ...
. Formally,
* A ''d-dimensional sphere in X'' is a continuous function .
* A ''d-dimensional ball in X'' is a continuous function .
* A ''d-dimensional-boundary hole'' in ''X'' is a ''d-''dimensional sphere that is not nullhomotopic
In topology, a branch of mathematics, two continuous functions from one topological space to another are called homotopic (from grc, ὁμός "same, similar" and "place") if one can be "continuously deformed" into the other, such a deforma ...
(- cannot be shrunk continuously to a point). Equivalently, it is a ''d-''dimensional sphere that cannot be continuously extended to a (''d''+1)-dimensional ball. It is sometimes called a (''d''+1)-dimensional hole (''d''+1 is the dimension of the "missing ball").
* ''X'' is called ''n''-connected if it contains no holes of boundary-dimension ''d'' ≤ ''n''.'
* The homotopical connectivity of ''X'', denoted , is the largest integer ''n'' for which X is ''n''-connected.
* A slightly different definition of connectivity, which makes some computations simpler, is: the smallest integer ''d'' such that X contains a ''d''-dimensional hole. This connectivity parameter is denoted by , and it differs from the previous parameter by 2, that is, .
Examples
 * A 2-dimensional hole (a hole with a 1-dimensional boundary) is a circle (S1) in ''X'', that cannot be shrunk continuously to a point in ''X''. An example is shown on the figure at the right. The yellow region is the topological space ''X''; it is a pentagon with a triangle removed. The blue circle is a 1-dimensional sphere in ''X''. It cannot be shrunk continuously to a point in X; therefore; X has a 2-dimensional hole. Another example is the
* A 2-dimensional hole (a hole with a 1-dimensional boundary) is a circle (S1) in ''X'', that cannot be shrunk continuously to a point in ''X''. An example is shown on the figure at the right. The yellow region is the topological space ''X''; it is a pentagon with a triangle removed. The blue circle is a 1-dimensional sphere in ''X''. It cannot be shrunk continuously to a point in X; therefore; X has a 2-dimensional hole. Another example is the punctured plane
This is a glossary of some terms used in the branch of mathematics known as topology. Although there is no absolute distinction between different areas of topology, the focus here is on general topology. The following definitions are also funda ...
- the Euclidean plane with a single point removed, . To make a 2-dimensional hole in a 3-dimensional ball, make a tunnel
A tunnel is an underground passageway, dug through surrounding soil, earth or rock, and enclosed except for the entrance and exit, commonly at each end. A pipeline is not a tunnel, though some recent tunnels have used immersed tube const ...
through it. In general, a space contains a 1-dimensional-boundary hole if and only if it is not simply-connected
In topology, a topological space is called simply connected (or 1-connected, or 1-simply connected) if it is path-connected and every path between two points can be continuously transformed (intuitively for embedded spaces, staying within the spac ...
. Hence, simply-connected is equivalent to 1-connected. ''X'' is 0-connected but not 1-connected, so . The lowest dimension of a hole is 2, so . * A 3-dimensional hole (a hole with a 2-dimensional boundary) is shown on the figure at the right. Here, ''X'' is a cube (yellow) with a ball removed (white). The 2-dimensional sphere (blue) cannot be continuously shrunk to a single point. ''X'' simply-connected but not 2-connected, so . The smallest dimension of a hole is 3, so .
* A 3-dimensional hole (a hole with a 2-dimensional boundary) is shown on the figure at the right. Here, ''X'' is a cube (yellow) with a ball removed (white). The 2-dimensional sphere (blue) cannot be continuously shrunk to a single point. ''X'' simply-connected but not 2-connected, so . The smallest dimension of a hole is 3, so .
 * For a 1-dimensional hole (a hole with a 0-dimensional boundary) we need to consider - the zero-dimensional sphere. What is a zero dimensional sphere? - For every integer ''d'', the sphere is the boundary of the (''d''+1)-dimensional ball . So is the boundary of , which is the segment ,1 Therefore, is the set of two disjoint points . A zero-dimensional sphere in ''X'' is just a set of two points in ''X''. If there is such a set, that cannot be continuously shrunk to a single point in ''X'' (or continuously extended to a segment in ''X''), this means that there is no path between the two points, that is, X is not
* For a 1-dimensional hole (a hole with a 0-dimensional boundary) we need to consider - the zero-dimensional sphere. What is a zero dimensional sphere? - For every integer ''d'', the sphere is the boundary of the (''d''+1)-dimensional ball . So is the boundary of , which is the segment ,1 Therefore, is the set of two disjoint points . A zero-dimensional sphere in ''X'' is just a set of two points in ''X''. If there is such a set, that cannot be continuously shrunk to a single point in ''X'' (or continuously extended to a segment in ''X''), this means that there is no path between the two points, that is, X is not path-connected
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint non-empty open subsets. Connectedness is one of the principal topological properties th ...
; see the figure at the right. Hence, path-connected is equivalent to 0-connected. ''X'' is not 0-connected, so . The lowest dimension of a hole is 1, so .
* A 0-dimensional hole is a missing 0-dimensional ball. A 0-dimensional ball is a single point; its boundary is an empty set. Therefore, the existence of a 0-dimensional hole is equivalent to the space being empty. Hence, non-empty is equivalent to (-1)-connected. For an empty space ''X'', and , which is its smallest possible value.
* A ball
A ball is a round object (usually spherical, but can sometimes be ovoid) with several uses. It is used in ball games, where the play of the game follows the state of the ball as it is hit, kicked or thrown by players. Balls can also be used fo ...
has no holes of any dimension. Therefore, its connectivity is infinite: .
Homotopical connectivity of spheres
In general, for every integer ''d'', (and )'''' The proof requires two directions: * Proving that , that is, cannot be continuously shrunk to a single point. This can be proved using the Borsuk–Ulam theorem. * Proving that , that is, that is, every continuous map for can be continuously shrunk to a single point.Definition using groups
A space ''X'' is called ''n''-connected, for ''n ≥'' 0, if it is non-empty, and all itshomotopy groups
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, denoted \pi_1(X), which records information about loops in a space. Intuitively, homo ...
of order ''d'' ≤ ''n'' are the trivial group
In mathematics, a trivial group or zero group is a group consisting of a single element. All such groups are isomorphic, so one often speaks of the trivial group. The single element of the trivial group is the identity element and so it is usuall ...
: where denotes the ''i''-th homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, denoted \pi_1(X), which records information about loops in a space. Intuitively, homot ...
and 0 denotes the trivial group. The two definitions are equivalent. The requirement for an ''n''-connected space consists of requirements for all ''d'' ≤ ''n'':
* The requirement for ''d''=-1 means that ''X'' should be nonempty.
* The requirement for ''d''=0 means that ''X'' should be path-connected.
* The requirement for any ''d'' ≥ 1 means that ''X'' contains no holes of boundary dimension ''d''. That is, every ''d''-dimensional sphere in ''X'' is homotopic to a constant map. Therefore, the ''d''-th homotopy group of ''X'' is trivial. The opposite is also true: If ''X'' has a hole with a ''d''-dimensional boundary, then there is a ''d''-dimensional sphere that is not homotopic to a constant map, so the ''d''-th homotopy group of ''X'' is not trivial. In short, X has a hole with a ''d''-dimensional boundary, if-and-only-if .The homotopical connectivity of ''X'' is the largest integer ''n'' for which X is ''n''-connected.
The requirements of being non-empty and path-connected can be interpreted as (−1)-connected and 0-connected, respectively, which is useful in defining 0-connected and 1-connected maps, as below. The ''0th homotopy set'' can be defined as:
:
This is only a pointed set
In mathematics, a pointed set (also based set or rooted set) is an ordered pair (X, x_0) where X is a set and x_0 is an element of X called the base point, also spelled basepoint.
Maps between pointed sets (X, x_0) and (Y, y_0) – called based m ...
, not a group, unless ''X'' is itself a topological group
In mathematics, topological groups are logically the combination of groups and topological spaces, i.e. they are groups and topological spaces at the same time, such that the continuity condition for the group operations connects these two s ...
; the distinguished point is the class of the trivial map, sending ''S''0 to the base point of ''X''. Using this set, a space is 0-connected if and only if the 0th homotopy set is the one-point set. The definition of homotopy groups and this homotopy set require that ''X'' be pointed (have a chosen base point), which cannot be done if ''X'' is empty.
A topological space ''X'' is path-connected
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint non-empty open subsets. Connectedness is one of the principal topological properties th ...
if and only if its 0th homotopy group vanishes identically, as path-connectedness implies that any two points ''x''1 and ''x''2 in ''X'' can be connected with a continuous path which starts in ''x''1 and ends in ''x''2, which is equivalent to the assertion that every mapping from ''S''0 (a discrete set
]
In mathematics, a point ''x'' is called an isolated point of a subset ''S'' (in a topological space ''X'') if ''x'' is an element of ''S'' and there exists a neighborhood of ''x'' which does not contain any other points of ''S''. This is equiva ...
of two points) to ''X'' can be deformed continuously to a constant map. With this definition, we can define ''X'' to be ''n''-connected if and only if
:
Examples
* A space ''X'' is (−1)-connected if and only if it is non-empty. * A space ''X'' is 0-connected if and only if it is non-empty andpath-connected
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint non-empty open subsets. Connectedness is one of the principal topological properties th ...
.
* A space is 1-connected if and only if it is simply connected
In topology, a topological space is called simply connected (or 1-connected, or 1-simply connected) if it is path-connected and every path between two points can be continuously transformed (intuitively for embedded spaces, staying within the space ...
.
* An ''n''-sphere is (''n'' − 1)-connected.
''n''-connected map
The corresponding ''relative'' notion to the ''absolute'' notion of an ''n''-connected ''space'' is an ''n''-connected ''map'', which is defined as a map whosehomotopy fiber In mathematics, especially homotopy theory, the homotopy fiber (sometimes called the mapping fiber)Joseph J. Rotman, ''An Introduction to Algebraic Topology'' (1988) Springer-Verlag ''(See Chapter 11 for construction.)'' is part of a construction ...
''Ff'' is an (''n'' − 1)-connected space. In terms of homotopy groups, it means that a map is ''n''-connected if and only if:
* is an isomorphism for , and
* is a surjection.
The last condition is frequently confusing; it is because the vanishing of the (''n'' − 1)-st homotopy group of the homotopy fiber In mathematics, especially homotopy theory, the homotopy fiber (sometimes called the mapping fiber)Joseph J. Rotman, ''An Introduction to Algebraic Topology'' (1988) Springer-Verlag ''(See Chapter 11 for construction.)'' is part of a construction ...
''Ff'' corresponds to a surjection on the ''n''th homotopy groups, in the exact sequence:
:
If the group on the right vanishes, then the map on the left is a surjection.
Low-dimensional examples:
* A connected map (0-connected map) is one that is onto path components (0th homotopy group); this corresponds to the homotopy fiber being non-empty.
* A simply connected map (1-connected map) is one that is an isomorphism on path components (0th homotopy group) and onto the fundamental group (1st homotopy group).
''n''-connectivity for spaces can in turn be defined in terms of ''n''-connectivity of maps: a space ''X'' with basepoint ''x''0 is an ''n''-connected space if and only if the inclusion of the basepoint is an ''n''-connected map. The single point set is contractible, so all its homotopy groups vanish, and thus "isomorphism below ''n'' and onto at ''n''" corresponds to the first ''n'' homotopy groups of ''X'' vanishing.
Interpretation
This is instructive for a subset: an ''n''-connected inclusion is one such that, up to dimension ''n'' − 1, homotopies in the larger space ''X'' can be homotoped into homotopies in the subset ''A''. For example, for an inclusion map to be 1-connected, it must be: * onto * one-to-one on and * onto One-to-one on means that if there is a path connecting two points by passing through ''X,'' there is a path in ''A'' connecting them, while onto means that in fact a path in ''X'' is homotopic to a path in ''A.'' In other words, a function which is an isomorphism on only implies that any elements of that are homotopic in ''X'' are ''abstractly'' homotopic in ''A'' – the homotopy in ''A'' may be unrelated to the homotopy in ''X'' – while being ''n''-connected (so also onto ) means that (up to dimension ''n'' − 1) homotopies in ''X'' can be pushed into homotopies in ''A''. This gives a more concrete explanation for the utility of the definition of ''n''-connectedness: for example, a space where the inclusion of the ''k''-skeleton is ''n''-connected (for ''n'' > ''k'') – such as the inclusion of a point in the ''n''-sphere – has the property that any cells in dimensions between ''k'' and ''n'' do not affect the lower-dimensional homotopy types.Lower bounds
Many topological proofs require lower bounds on the homotopical connectivity. There are several "recipes" for proving such lower bounds.Homology
Hurewicz theorem relates the homotopical connectivity to the homological connectivity'','' denoted by . This is useful for computing homotopical connectivity, since the homological groups can be computed more easily. Suppose first that ''X'' is simply-connected, that is, . Let ; so for all