Montgomery's Pair Correlation Conjecture

In mathematics, Montgomery's pair correlation conjecture is a conjecture made by that the pair correlation between pairs of zeros of the Riemann zeta function (normalized to have unit average spacing) is
:$1-\left(\frac\right)^ + \delta(u),$
which, as Freeman Dyson pointed out to him, is the same as the pair correlation function of random Hermitian matrices.

Conjecture

''Under the assumption that the Riemann Hypothesis is true.''

Let $\alpha\leq \beta$ be fixed, as $T\to \infty$''
: N(T;\alpha,\beta)\, := \, \sum_ 1 \, \sim \, \left( \int\limits_\alpha^\beta \left(1-\left(\frac\right)^2 \right) \mathrmu +\delta_( alpha,\beta\right)\frac\log\frac

and we count over $A = \$, where each $\gamma, \gamma'$ is the imaginary part of the non-trivial zeros of zeta function, that is $\tfrac+i\gamma$. Also $\delta_0$ denotes the delta measure supported at 0.

Explanation

Informally, this means that the chance of finding a zero in a very short interval of length 2π''L''/log(''T'') at a distance 2π''u''/log(''T'') from a zero 1/2+''iT'' is about ''L'' times the expression above. (The factor 2π/log(''T'') is a normalization factor that can be thought of informally as the average spacing between zeros with imaginary part about ''T''.) showed that the conjecture was supported by large-scale computer calculations of the zeros. The conjecture has been extended to correlations of more than two zeros, and also to zeta functions of automorphic representations . In 1982 a student of Montgomery's, Ali Erhan Özlük, proved the pair correlation conjecture for some of Dirichlet's L-functions.

The connection with random unitary matrices could lead to a proof of the Riemann hypothesis (RH). The Hilbert–Pólya conjecture asserts that the zeros of the Riemann Zeta function correspond to the eigenvalues of a linear operator, and implies RH. Some people think this is a promising approach ().

Montgomery was studying the Fourier transform ''F''(''x'') of the pair correlation function, and showed (assuming the Riemann hypothesis) that it was
equal to , ''x'', for , ''x'', < 1. His methods were unable to determine it for , ''x'', ≥ 1, but he conjectured that it was equal to 1 for these ''x'', which implies that the pair correlation function is as above. He was also motivated by the notion that the Riemann hypothesis is not a brick wall, and one should feel free to make ''stronger'' conjectures.

F(α) conjecture or strong pair correlation conjecture

Let again $\tfrac+i\gamma$ and $\tfrac+i\gamma'$ stand for non-trivial zeros of the Riemann zeta function. Montgomery introduced the function
:$F(\alpha):=F_T(\alpha)=\left(\frac\log(T)\right)^\sum\limits_T^w(\gamma-\gamma')$
for $T>2,\;\alpha\in \mathbb$ and some weight function $w(u):=\tfrac$.

Montgomery and Goldstone proved under the Riemann hypothesis, that for $, \alpha, \leq 1$ this function converges uniformly
:$F(\alpha)=T^\log (T)(1+\mathcal(1))+, \alpha, +\mathcal(1),\quad T\to \infty.$

Montgomery conjectured, which is now known as the ''F(α) conjecture'' or ''strong pair correlation conjecture'', that for $, \alpha, > 1$ we have uniform convergence
:$F(\alpha)=1+\mathcal(1),\quad T\to \infty$
for $\alpha$ in a bounded interval.

Numerical calculation by Odlyzko

In the 1980s, motivated by the Montgomery's conjecture, Odlyzko began an intensive numerical study of the statistics of the zeros of ζ(''s''). He confirmed that the distribution of the spacings between non-trivial zeros using detail numerical calculation and demonstrated that the Montgomery's conjecture would be true and the distribution would agree with the distribution of spacings of GUE random matrix eigenvalues using Cray X-MP. In 1987 he reported the calculations in the paper .

For non-trivial zero, 1/2 + iγ_''n'', let the normalized spacings be
:$\delta_n = \frac\, .$
Then we would expect the following formula as the limit for $M, N \to\infty$:

:$\frac \ \sim \int_^ \left( 1- \biggl( \frac \biggr)^2 \right) du$

Based on a new algorithm developed by Odlyzko and Schönhage that allowed them to compute a value of ζ(1/2 + i''t'') in an average time of ''t''^ε steps, Odlyzko computed millions of zeros at heights around 10²⁰ and gave some evidence for the GUE conjecture.A. M. Odlyzko, "The 10²⁰-th zero of the Riemann zeta function and 70 million of its neighbors," AT&T Bell Lab. preprint (1989)M. Mehta (1990), chap.1

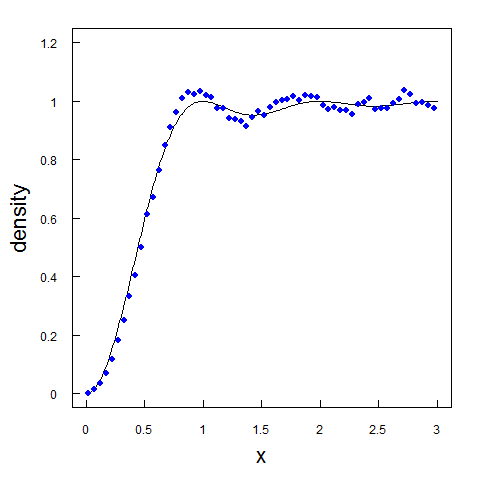
The figure contains the first 10⁵ non-trivial zeros of the Riemann zeta function. As more zeros are sampled, the more closely their distribution approximates the shape of the GUE random matrix.

See also

* Lehmer pair

References

*
*
*
*
*{{Citation , author2-link=Peter Sarnak , last1=Rudnick , first1=Zeév , last2=Sarnak , first2=Peter , title=Zeros of principal L-functions and random matrix theory , doi=10.1215/S0012-7094-96-08115-6 , mr=1395406 , year=1996 , journal=Duke Mathematical Journal , issn=0012-7094 , volume=81 , issue=2 , pages=269–322

Zeta and L-functions
Conjectures
Unsolved problems in number theory
Analytic number theory
Random matrices