Mild-slope equation on:
[Wikipedia]
[Google]
[Amazon]
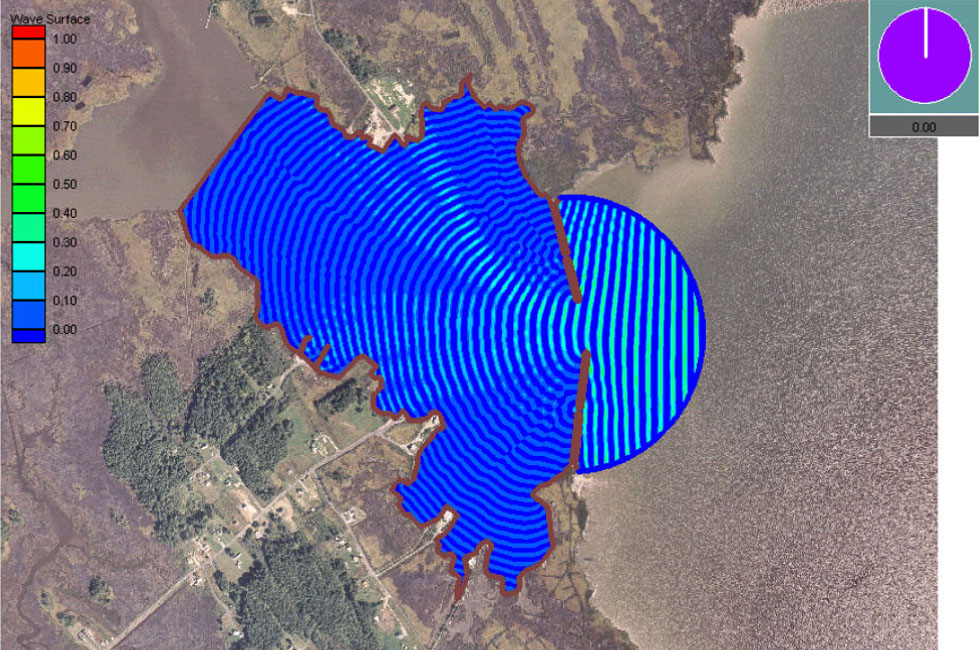 In
In
 In
In fluid dynamics
In physics, physical chemistry and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids – liquids and gases. It has several subdisciplines, including (the study of air and other gases in motion ...
, the mild-slope equation describes the combined effects of diffraction
Diffraction is the deviation of waves from straight-line propagation without any change in their energy due to an obstacle or through an aperture. The diffracting object or aperture effectively becomes a secondary source of the Wave propagation ...
and refraction
In physics, refraction is the redirection of a wave as it passes from one transmission medium, medium to another. The redirection can be caused by the wave's change in speed or by a change in the medium. Refraction of light is the most commo ...
for water wave
In fluid dynamics, a wind wave, or wind-generated water wave, is a surface wave that occurs on the free surface of bodies of water as a result of the wind blowing over the water's surface. The contact distance in the direction of the wind is ...
s propagating over bathymetry
Bathymetry (; ) is the study of underwater depth of ocean floors ('' seabed topography''), river floors, or lake floors. In other words, bathymetry is the underwater equivalent to hypsometry or topography. The first recorded evidence of wate ...
and due to lateral boundaries—like breakwaters and coastline
A coast (coastline, shoreline, seashore) is the land next to the sea or the line that forms the boundary between the land and the ocean or a lake. Coasts are influenced by the topography of the surrounding landscape and by aquatic erosion, su ...
s. It is an approximate model, deriving its name from being originally developed for wave propagation over mild slopes of the sea floor. The mild-slope equation is often used in coastal engineering
Coastal engineering is a branch of civil engineering concerned with the specific demands posed by constructing at or near the coast, as well as the development of the coast itself.
The fluid dynamics, hydrodynamic impact of especially wind wave, ...
to compute the wave-field changes near harbour
A harbor (American English), or harbour (Commonwealth English; see American and British English spelling differences#-our, -or, spelling differences), is a sheltered body of water where ships, boats, and barges can be Mooring, moored. The t ...
s and coast
A coast (coastline, shoreline, seashore) is the land next to the sea or the line that forms the boundary between the land and the ocean or a lake. Coasts are influenced by the topography of the surrounding landscape and by aquatic erosion, su ...
s.
The mild-slope equation models the propagation and transformation of water waves, as they travel through waters of varying depth and interact with lateral boundaries such as cliff
In geography and geology, a cliff or rock face is an area of Rock (geology), rock which has a general angle defined by the vertical, or nearly vertical. Cliffs are formed by the processes of weathering and erosion, with the effect of gravity. ...
s, beach
A beach is a landform alongside a body of water which consists of loose particles. The particles composing a beach are typically made from Rock (geology), rock, such as sand, gravel, shingle beach, shingle, pebbles, etc., or biological s ...
es, seawall
A seawall (or sea wall) is a form of coastal defense constructed where the sea, and associated coastal processes, impact directly upon the landforms of the coast. The purpose of a seawall is to protect areas of human habitation, conservation, ...
s and breakwaters. As a result, it describes the variations in wave amplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of am ...
, or equivalently wave height
In fluid dynamics, the wave height of a surface wave is the difference between the elevations of a crest and a neighboring trough. ''Wave height'' is a term used by mariners, as well as in coastal, ocean and naval engineering.
At sea, the ...
. From the wave amplitude, the amplitude of the flow velocity
In continuum mechanics the flow velocity in fluid dynamics, also macroscopic velocity in statistical mechanics, or drift velocity in electromagnetism, is a vector field used to mathematically describe the motion of a continuum. The length of the f ...
oscillations underneath the water surface can also be computed. These quantities—wave amplitude and flow-velocity amplitude—may subsequently be used to determine the wave effects on coastal and offshore structures, ships and other floating objects, sediment transport
Sediment transport is the movement of solid particles (sediment), typically due to a combination of gravity acting on the sediment, and the movement of the fluid in which the sediment is entrained. Sediment transport occurs in natural systems wh ...
and resulting bathymetric changes of the sea bed and coastline, mean flow fields and mass transfer
Mass transfer is the net movement of mass from one location (usually meaning stream, phase, fraction, or component) to another. Mass transfer occurs in many processes, such as absorption, evaporation, drying, precipitation, membrane filtra ...
of dissolved and floating materials. Most often, the mild-slope equation is solved by computer using methods from numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic computation, symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of ...
.
A first form of the mild-slope equation was developed by Eckart in 1952, and an improved version—the mild-slope equation in its classical formulation—has been derived independently by Juri Berkhoff in 1972. Thereafter, many modified and extended forms have been proposed, to include the effects of, for instance: wave–current interaction, wave nonlinearity
In mathematics and science, a nonlinear system (or a non-linear system) is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathe ...
, steeper sea-bed slopes, bed friction and wave breaking. Also parabolic approximations to the mild-slope equation are often used, in order to reduce the computational cost.
In case of a constant depth, the mild-slope equation reduces to the Helmholtz equation
In mathematics, the Helmholtz equation is the eigenvalue problem for the Laplace operator. It corresponds to the elliptic partial differential equation:
\nabla^2 f = -k^2 f,
where is the Laplace operator, is the eigenvalue, and is the (eigen)fun ...
for wave diffraction.
Formulation for monochromatic wave motion
Formonochromatic
A monochrome or monochromatic image, object or palette is composed of one color (or values of one color). Images using only shades of grey are called grayscale (typically digital) or black-and-white (typically analog). In physics, mon ...
waves according to linear theory—with the free surface
In physics, a free surface is the surface of a fluid that is subject to zero parallel shear stress,
such as the interface between two homogeneous fluids.
An example of two such homogeneous fluids would be a body of water (liquid) and the air in ...
elevation given as and the waves propagating on a fluid layer of mean
A mean is a quantity representing the "center" of a collection of numbers and is intermediate to the extreme values of the set of numbers. There are several kinds of means (or "measures of central tendency") in mathematics, especially in statist ...
water depth —the mild-slope equation is:
where:
* is the complex-valued amplitude of the free-surface elevation
* is the horizontal position;
* is the angular frequency
In physics, angular frequency (symbol ''ω''), also called angular speed and angular rate, is a scalar measure of the angle rate (the angle per unit time) or the temporal rate of change of the phase argument of a sinusoidal waveform or sine ...
of the monochromatic wave motion;
* is the imaginary unit
The imaginary unit or unit imaginary number () is a mathematical constant that is a solution to the quadratic equation Although there is no real number with this property, can be used to extend the real numbers to what are called complex num ...
;
* means taking the real part
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form ...
of the quantity between braces;
* is the horizontal gradient
In vector calculus, the gradient of a scalar-valued differentiable function f of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p gives the direction and the rate of fastest increase. The g ...
operator;
* is the divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the rate that the vector field alters the volume in an infinitesimal neighborhood of each point. (In 2D this "volume" refers to ...
operator;
* is the wavenumber
In the physical sciences, the wavenumber (or wave number), also known as repetency, is the spatial frequency of a wave. Ordinary wavenumber is defined as the number of wave cycles divided by length; it is a physical quantity with dimension of ...
;
* is the phase speed
The phase velocity of a wave is the rate at which the wave propagates in any medium. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, ...
of the waves and
* is the group speed of the waves.
The phase and group speed depend on the dispersion relation
In the physical sciences and electrical engineering, dispersion relations describe the effect of dispersion on the properties of waves in a medium. A dispersion relation relates the wavelength or wavenumber of a wave to its frequency. Given the ...
, and are derived from Airy wave theory as:
where
* is Earth's gravity
The gravity of Earth, denoted by , is the net acceleration that is imparted to objects due to the combined effect of gravitation (from mass distribution within Earth) and the centrifugal force (from the Earth's rotation).
It is a vector qu ...
and
* is the hyperbolic tangent
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the ...
.
For a given angular frequency , the wavenumber has to be solved from the dispersion equation, which relates these two quantities to the water depth .
Transformation to an inhomogeneous Helmholtz equation
Through the transformation the mild slope equation can be cast in the form of an inhomogeneous Helmholtz equation: where is theLaplace operator
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a Scalar field, scalar function on Euclidean space. It is usually denoted by the symbols \nabla\cdot\nabla, \nabla^2 (where \ ...
.
Propagating waves
In spatiallycoherent
Coherence is, in general, a state or situation in which all the parts or ideas fit together well so that they form a united whole.
More specifically, coherence, coherency, or coherent may refer to the following:
Physics
* Coherence (physics ...
fields of propagating waves, it is useful to split the complex amplitude in its amplitude and phase, both real valued:
where
* is the amplitude or absolute value
In mathematics, the absolute value or modulus of a real number x, is the non-negative value without regard to its sign. Namely, , x, =x if x is a positive number, and , x, =-x if x is negative (in which case negating x makes -x positive), ...
of and
* is the wave phase, which is the argument
An argument is a series of sentences, statements, or propositions some of which are called premises and one is the conclusion. The purpose of an argument is to give reasons for one's conclusion via justification, explanation, and/or persu ...
of
This transforms the mild-slope equation in the following set of equations (apart from locations for which is singular):
where
* is the average
In colloquial, ordinary language, an average is a single number or value that best represents a set of data. The type of average taken as most typically representative of a list of numbers is the arithmetic mean the sum of the numbers divided by ...
wave-energy density per unit horizontal area (the sum of the kinetic and potential energy
In physics, potential energy is the energy of an object or system due to the body's position relative to other objects, or the configuration of its particles. The energy is equal to the work done against any restoring forces, such as gravity ...
densities),
* is the effective wavenumber vector, with components
* is the effective group velocity
The group velocity of a wave is the velocity with which the overall envelope shape of the wave's amplitudes—known as the ''modulation'' or ''envelope (waves), envelope'' of the wave—propagates through space.
For example, if a stone is thro ...
vector,
* is the fluid density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
, and
* is the acceleration by the Earth's gravity
The gravity of Earth, denoted by , is the net acceleration that is imparted to objects due to the combined effect of gravitation (from mass distribution within Earth) and the centrifugal force (from the Earth's rotation).
It is a vector qu ...
.
The last equation shows that wave energy is conserved in the mild-slope equation, and that the wave energy is transported in the -direction normal to the wave crests (in this case of pure wave motion without mean currents). The effective group speed is different from the group speed
The first equation states that the effective wavenumber is irrotational
In vector calculus, a conservative vector field is a vector field that is the gradient of some function. A conservative vector field has the property that its line integral is path independent; the choice of path between two points does not chan ...
, a direct consequence of the fact it is the derivative of the wave phase , a scalar field
In mathematics and physics, a scalar field is a function associating a single number to each point in a region of space – possibly physical space. The scalar may either be a pure mathematical number ( dimensionless) or a scalar physical ...
. The second equation is the eikonal equation
An eikonal equation (from Greek εἰκών, image) is a non-linear first-order partial differential equation that is encountered in problems of wave propagation.
The classical eikonal equation in geometric optics is a differential equation of t ...
. It shows the effects of diffraction on the effective wavenumber: only for more-or-less progressive waves, with the splitting into amplitude and phase leads to consistent-varying and meaningful fields of and . Otherwise, ''κ''2 can even become negative. When the diffraction effects are totally neglected, the effective wavenumber ''κ'' is equal to , and the geometric optics
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician ...
approximation for wave refraction
In physics, refraction is the redirection of a wave as it passes from one transmission medium, medium to another. The redirection can be caused by the wave's change in speed or by a change in the medium. Refraction of light is the most commo ...
can be used.
When is used in the mild-slope equation, the result is, apart from a factor :
Now both the real part and the imaginary part of this equation have to be equal to zero:
The effective wavenumber vector is ''defined'' as the gradient of the wave phase:
and its vector length is
Note that is an irrotational
In vector calculus, a conservative vector field is a vector field that is the gradient of some function. A conservative vector field has the property that its line integral is path independent; the choice of path between two points does not chan ...
field, since the curl of the gradient is zero:
Now the real and imaginary parts of the transformed mild-slope equation become, first multiplying the imaginary part by :
The first equation directly leads to the eikonal equation above for , while the second gives:
which—by noting that in which the angular frequency is a constant for time-harmonic
In physics, acoustics, and telecommunications, a harmonic is a sinusoidal wave with a frequency that is a positive integer multiple of the ''fundamental frequency'' of a periodic signal. The fundamental frequency is also called the ''1st har ...
motion—leads to the wave-energy conservation equation.
Derivation of the mild-slope equation
The mild-slope equation can be derived by the use of several methods. Here, we will use a variational approach. The fluid is assumed to beinviscid
Viscosity is a measure of a fluid's rate-dependent resistance to a change in shape or to movement of its neighboring portions relative to one another. For liquids, it corresponds to the informal concept of ''thickness''; for example, syrup h ...
and incompressible
Incompressible may refer to:
* Incompressible flow, in fluid mechanics
* incompressible vector field, in mathematics
* Incompressible surface, in mathematics
* Incompressible string, in computing
{{Disambig ...
, and the flow is assumed to be irrotational
In vector calculus, a conservative vector field is a vector field that is the gradient of some function. A conservative vector field has the property that its line integral is path independent; the choice of path between two points does not chan ...
. These assumptions are valid ones for surface gravity waves, since the effects of vorticity
In continuum mechanics, vorticity is a pseudovector (or axial vector) field that describes the local spinning motion of a continuum near some point (the tendency of something to rotate), as would be seen by an observer located at that point an ...
and viscosity
Viscosity is a measure of a fluid's rate-dependent drag (physics), resistance to a change in shape or to movement of its neighboring portions relative to one another. For liquids, it corresponds to the informal concept of ''thickness''; for e ...
are only significant in the Stokes boundary layers (for the oscillatory part of the flow). Because the flow is irrotational, the wave motion can be described using potential flow
In fluid dynamics, potential flow or irrotational flow refers to a description of a fluid flow with no vorticity in it. Such a description typically arises in the limit of vanishing viscosity, i.e., for an inviscid fluid and with no vorticity pre ...
theory.
Luke's variational principle
Luke's Lagrangian formulation gives a variational formulation fornon-linear
In mathematics and science, a nonlinear system (or a non-linear system) is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathe ...
surface gravity waves.
For the case of a horizontally unbounded domain with a constant density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
, a free fluid surface at and a fixed sea bed at Luke's variational principle uses the Lagrangian
where is the horizontal Lagrangian density, given by:
where is the velocity potential
A velocity potential is a scalar potential used in potential flow theory. It was introduced by Joseph-Louis Lagrange in 1788.
It is used in continuum mechanics, when a continuum occupies a simply-connected region and is irrotational. In such a ca ...
, with the flow velocity
In continuum mechanics the flow velocity in fluid dynamics, also macroscopic velocity in statistical mechanics, or drift velocity in electromagnetism, is a vector field used to mathematically describe the motion of a continuum. The length of the f ...
components being and in the , and directions, respectively.
Luke's Lagrangian formulation can also be recast into a Hamiltonian formulation in terms of the surface elevation and velocity potential at the free surface.
Taking the variations of with respect to the potential and surface elevation leads to the Laplace equation
In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties in 1786. This is often written as
\nabla^2\! f = 0 or \Delta f = 0,
where \Delt ...
for in the fluid interior, as well as all the boundary conditions both on the free surface as at the bed at
Linear wave theory
In case of linear wave theory, the vertical integral in the Lagrangian density is split into a part from the bed to the mean surface at and a second part from to the free surface . Using aTaylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor ser ...
expansion for the second integral around the mean free-surface elevation and only retaining quadratic terms in and the Lagrangian density for linear wave motion becomes
The term in the vertical integral is dropped since it has become dynamically uninteresting: it gives a zero contribution to the Euler–Lagrange equation
In the calculus of variations and classical mechanics, the Euler–Lagrange equations are a system of second-order ordinary differential equations whose solutions are stationary points of the given action functional. The equations were discovered ...
s, with the upper integration limit now fixed. The same is true for the neglected bottom term proportional to in the potential energy.
The waves propagate in the horizontal plane, while the structure of the potential is not wave-like in the vertical -direction. This suggests the use of the following assumption on the form of the potential
with normalisation at the mean free-surface elevation
Here is the velocity potential at the mean free-surface level Next, the mild-slope assumption is made, in that the vertical shape function changes slowly in the -plane, and horizontal derivatives of can be neglected in the flow velocity. So:
As a result:
with
The Euler–Lagrange equation
In the calculus of variations and classical mechanics, the Euler–Lagrange equations are a system of second-order ordinary differential equations whose solutions are stationary points of the given action functional. The equations were discovered ...
s for this Lagrangian density are, with representing either or
Now is first taken equal to and then to
As a result, the evolution equations for the wave motion become:
with the horizontal gradient operator: where superscript denotes the transpose
In linear algebra, the transpose of a Matrix (mathematics), matrix is an operator which flips a matrix over its diagonal;
that is, it switches the row and column indices of the matrix by producing another matrix, often denoted by (among other ...
.
The next step is to choose the shape function and to determine and
Vertical shape function from Airy wave theory
Since the objective is the description of waves over mildly sloping beds, the shape function is chosen according to Airy wave theory. This is the linear theory of waves propagating in constant depth The form of the shape function is: with now in general not a constant, but chosen to vary with and according to the local depth and the linear dispersion relation: Here a constant angular frequency, chosen in accordance with the characteristics of the wave field under study. Consequently, the integrals and become: The following time-dependent equations give the evolution of the free-surface elevation and free-surface potential From the two evolution equations, one of the variables or can be eliminated, to obtain the time-dependent form of the mild-slope equation: and the corresponding equation for the free-surface potential is identical, with replaced by The time-dependent mild-slope equation can be used to model waves in a narrow band of frequencies aroundMonochromatic waves
Consider monochromatic waves with complex amplitude and angular frequency : with and chosen equal to each other, Using this in the time-dependent form of the mild-slope equation, recovers the classical mild-slope equation for time-harmonic wave motion:Applicability and validity of the mild-slope equation
The standard mild slope equation, without extra terms for bed slope and bed curvature, provides accurate results for the wave field over bed slopes ranging from 0 to about 1/3. However, some subtle aspects, like the amplitude of reflected waves, can be completely wrong, even for slopes going to zero. This mathematical curiosity has little practical importance in general since this reflection becomes vanishingly small for small bottom slopes.Notes
References
*, 2 Parts, 967 pages. * *, 740 pages. * * {{physical oceanography Coastal geography Equations of fluid dynamics Water waves