Mercator Projection on:
[Wikipedia]
[Google]
[Amazon]
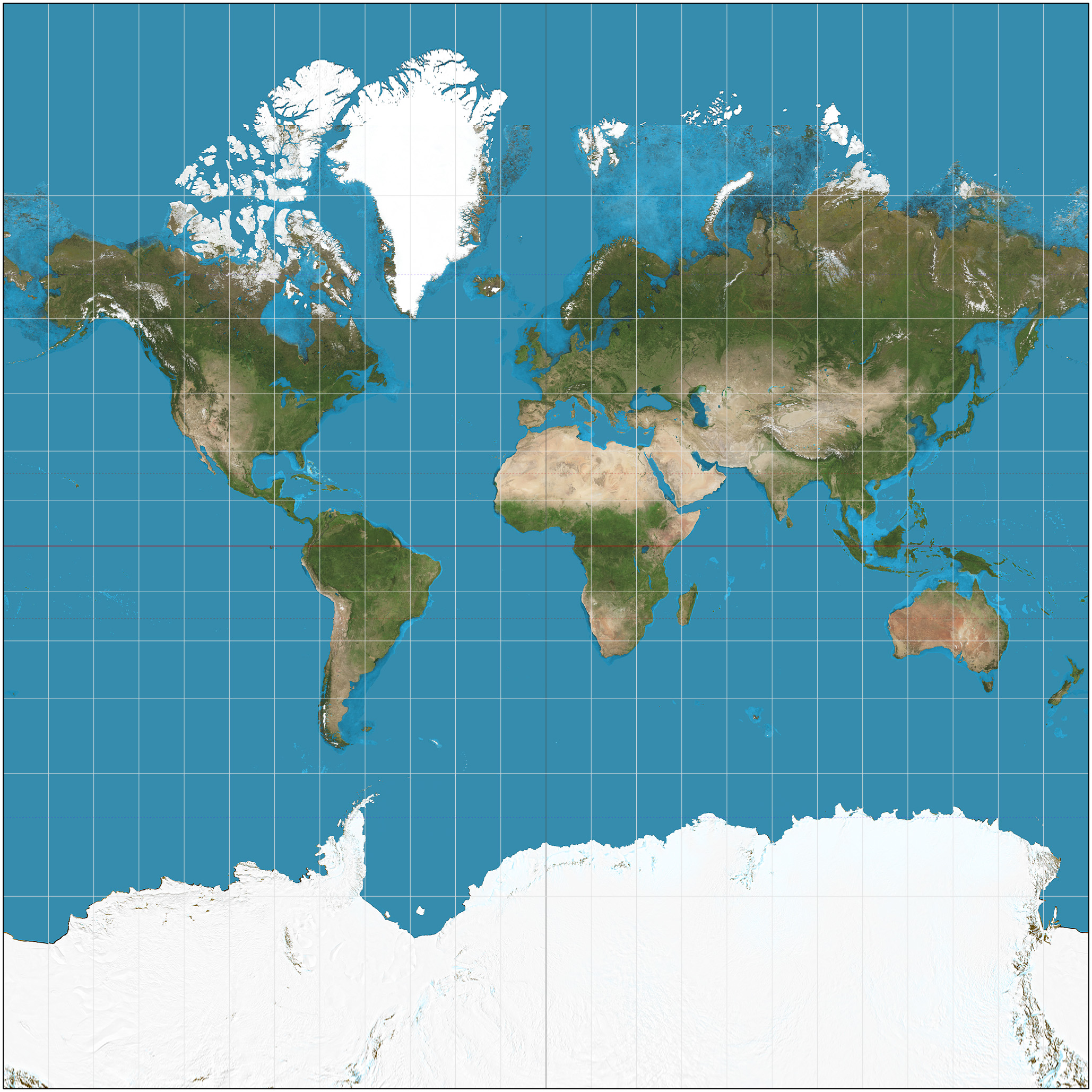

 The Mercator projection () is a
The Mercator projection () is a
 As on all
As on all
 The Mercator projection was designed for use in marine
The Mercator projection was designed for use in marine
 A cylindrical map projection is specified by formulae linking the geographic coordinates of latitude ''φ'' and longitude ''λ'' to Cartesian coordinates on the map with origin on the equator and ''x''-axis along the equator. By construction, all points on the same meridian lie on the same ''generator'' of the cylinder at a constant value of ''x'', but the distance ''y'' along the generator (measured from the equator) is an arbitrary function of latitude, ''y''(''φ''). In general this function does not describe the geometrical projection (as of light rays onto a screen) from the centre of the globe to the cylinder, which is only one of an unlimited number of ways to conceptually project a cylindrical map.
Since the cylinder is tangential to the globe at the equator, the
A cylindrical map projection is specified by formulae linking the geographic coordinates of latitude ''φ'' and longitude ''λ'' to Cartesian coordinates on the map with origin on the equator and ''x''-axis along the equator. By construction, all points on the same meridian lie on the same ''generator'' of the cylinder at a constant value of ''x'', but the distance ''y'' along the generator (measured from the equator) is an arbitrary function of latitude, ''y''(''φ''). In general this function does not describe the geometrical projection (as of light rays onto a screen) from the centre of the globe to the cylinder, which is only one of an unlimited number of ways to conceptually project a cylindrical map.
Since the cylinder is tangential to the globe at the equator, the
 The graph shows the variation of this scale factor with latitude. Some numerical values are listed below.
:at latitude 30° the scale factor is ''k'' = sec 30° = 1.15,
:at latitude 45° the scale factor is ''k'' = sec 45° = 1.41,
:at latitude 60° the scale factor is ''k'' = sec 60° = 2,
:at latitude 80° the scale factor is ''k'' = sec 80° = 5.76,
:at latitude 85° the scale factor is ''k'' = sec 85° = 11.5
The area scale factor is the product of the parallel and meridian scales . For Greenland, taking 73° as a median latitude, ''hk'' = 11.7. For Australia, taking 25° as a median latitude, ''hk'' = 1.2. For Great Britain, taking 55° as a median latitude, ''hk'' = 3.04.
The variation with latitude is sometimes indicated by multiple bar scales as shown below.
The graph shows the variation of this scale factor with latitude. Some numerical values are listed below.
:at latitude 30° the scale factor is ''k'' = sec 30° = 1.15,
:at latitude 45° the scale factor is ''k'' = sec 45° = 1.41,
:at latitude 60° the scale factor is ''k'' = sec 60° = 2,
:at latitude 80° the scale factor is ''k'' = sec 80° = 5.76,
:at latitude 85° the scale factor is ''k'' = sec 85° = 11.5
The area scale factor is the product of the parallel and meridian scales . For Greenland, taking 73° as a median latitude, ''hk'' = 11.7. For Australia, taking 25° as a median latitude, ''hk'' = 1.2. For Great Britain, taking 55° as a median latitude, ''hk'' = 3.04.
The variation with latitude is sometimes indicated by multiple bar scales as shown below.
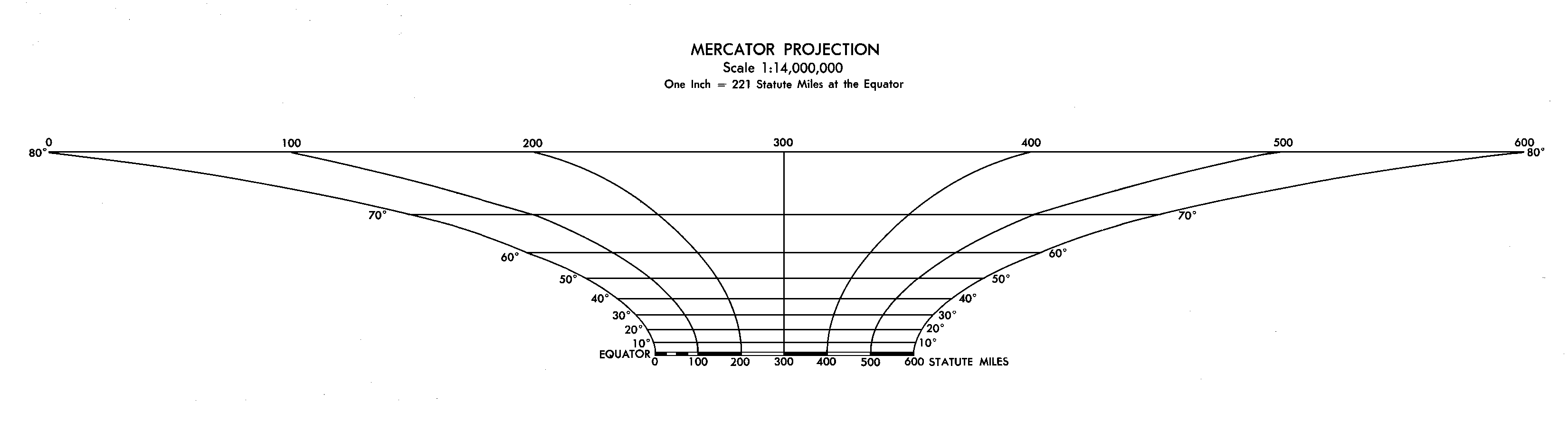
 The classic way of showing the distortion inherent in a projection is to use Tissot's indicatrix. Nicolas Tissot noted that the scale factors at a point on a map projection, specified by the numbers ''h'' and ''k'', define an ellipse at that point. For cylindrical projections, the axes of the ellipse are aligned to the meridians and parallels. Snyder. Working Manual, page 20. For the Mercator projection, ''h'' = ''k'', so the ellipses degenerate into circles with radius proportional to the value of the scale factor for that latitude. These circles are rendered on the projected map with extreme variation in size, indicative of Mercator's scale variations.
The classic way of showing the distortion inherent in a projection is to use Tissot's indicatrix. Nicolas Tissot noted that the scale factors at a point on a map projection, specified by the numbers ''h'' and ''k'', define an ellipse at that point. For cylindrical projections, the axes of the ellipse are aligned to the meridians and parallels. Snyder. Working Manual, page 20. For the Mercator projection, ''h'' = ''k'', so the ellipses degenerate into circles with radius proportional to the value of the scale factor for that latitude. These circles are rendered on the projected map with extreme variation in size, indicative of Mercator's scale variations.
4.26#ii
an
4.23#viii
/ref> :
The function ''y''(''φ'') is plotted alongside ''φ'' for the case ''R'' = 1: it tends to infinity at the poles. The linear ''y''-axis values are not usually shown on printed maps; instead some maps show the non-linear scale of latitude values on the right. More often than not the maps show only a graticule of selected meridians and parallels.
:
The function ''y''(''φ'') is plotted alongside ''φ'' for the case ''R'' = 1: it tends to infinity at the poles. The linear ''y''-axis values are not usually shown on printed maps; instead some maps show the non-linear scale of latitude values on the right. More often than not the maps show only a graticule of selected meridians and parallels.
 For small elements, the angle PKQ is approximately a right angle and therefore
:
The previously mentioned scaling factors from globe to cylinder are given by
:''parallel scale factor''
:''meridian scale factor''
Since the meridians are mapped to lines of constant ''x'', we must have and ''δx'' = ''Rδλ'', (''λ'' in radians). Therefore, in the limit of infinitesimally small elements
:
In the case of the Mercator projection, ''y(''φ'') = ''R'' sec ''φ'', so this gives us ''h'' = ''k'' and ''α'' = ''β''. The fact that ''h'' = ''k'' is the isotropy of scale factors discussed above. The fact that ''α'' = ''β'' reflects another implication of the mapping being conformal, namely the fact that a sailing course of constant azimuth on the globe is mapped into the same constant grid bearing on the map.
For small elements, the angle PKQ is approximately a right angle and therefore
:
The previously mentioned scaling factors from globe to cylinder are given by
:''parallel scale factor''
:''meridian scale factor''
Since the meridians are mapped to lines of constant ''x'', we must have and ''δx'' = ''Rδλ'', (''λ'' in radians). Therefore, in the limit of infinitesimally small elements
:
In the case of the Mercator projection, ''y(''φ'') = ''R'' sec ''φ'', so this gives us ''h'' = ''k'' and ''α'' = ''β''. The fact that ''h'' = ''k'' is the isotropy of scale factors discussed above. The fact that ''α'' = ''β'' reflects another implication of the mapping being conformal, namely the fact that a sailing course of constant azimuth on the globe is mapped into the same constant grid bearing on the map.
USGS pages.
It gives full details of most projections, together with interesting introductory sections, but it does not derive any of the projections from first principles.
– contains high-resolution images of the 1569 world map by Mercator.
Table of examples and properties of all common projections
from radicalcartography.net.
* ttp://www.hydrometronics.com/downloads/Web%20Mercator%20-%20Non-Conformal,%20Non-Mercator%20(notes).pdf Web Mercator: Non-Conformal, Non-Mercator (Noel Zinn, Hydrometronics LLC)br>Mercator's Projection at University of British Columbia
{{Authority control Conformal projections Map projections 16th-century inventions Early modern Netherlandish cartography
 The Mercator projection () is a
The Mercator projection () is a cylindrical map projection
In cartography, map projection is the term used to describe a broad set of transformations employed to represent the two-dimensional curved surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitu ...
presented by Flemish
Flemish (''Vlaams'') is a Low Franconian dialect cluster of the Dutch language. It is sometimes referred to as Flemish Dutch (), Belgian Dutch ( ), or Southern Dutch (). Flemish is native to Flanders, a historical region in northern Belgium; ...
geographer and cartographer Gerardus Mercator
Gerardus Mercator (; 5 March 1512 – 2 December 1594) was a 16th-century geographer, cosmographer and Cartography, cartographer from the County of Flanders. He is most renowned for creating the Mercator 1569 world map, 1569 world map based on ...
in 1569. It became the standard map projection for navigation
Navigation is a field of study that focuses on the process of monitoring and controlling the movement of a craft or vehicle from one place to another.Bowditch, 2003:799. The field of navigation includes four general categories: land navigation, ...
because it is unique in representing north as up and south as down everywhere while preserving local directions and shapes. The map is thereby conformal. As a side effect, the Mercator projection inflates the size of objects away from the equator. This inflation is very small near the equator but accelerates with increasing latitude
In geography, latitude is a coordinate that specifies the north– south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north pol ...
to become infinite at the poles. As a result, landmasses such as Greenland
Greenland ( kl, Kalaallit Nunaat, ; da, Grønland, ) is an island country in North America that is part of the Kingdom of Denmark. It is located between the Arctic and Atlantic oceans, east of the Canadian Arctic Archipelago. Greenland i ...
, Antarctica
Antarctica () is Earth's southernmost and least-populated continent. Situated almost entirely south of the Antarctic Circle and surrounded by the Southern Ocean, it contains the geographic South Pole. Antarctica is the fifth-largest cont ...
and Russia
Russia (, , ), or the Russian Federation, is a transcontinental country spanning Eastern Europe and Northern Asia. It is the largest country in the world, with its internationally recognised territory covering , and encompassing one-eig ...
appear far larger than they actually are relative to landmasses near the equator, such as Central Africa.
History
There is some controversy over the origins of the Mercator. Germanpolymath
A polymath ( el, πολυμαθής, , "having learned much"; la, homo universalis, "universal human") is an individual whose knowledge spans a substantial number of subjects, known to draw on complex bodies of knowledge to solve specific pro ...
Erhard Etzlaub
Erhard Etzlaub ( 1455 1465 – 1532) was a German astronomer, geodesist, cartographer, instrument maker and physician.
Life
Little is known of Etzlaub's life. One "Erhart Etzlauber" became a citizen of Nuremberg in 1484, but his profession was n ...
engraved miniature "compass maps" (about 10×8 cm) of Europe and parts of Africa that spanned latitudes 0°–67° to allow adjustment of his portable pocket-size sundials
A sundial is a horological device that tells the time of day (referred to as civil time in modern usage) when direct sunlight shines by the apparent position of the Sun in the sky. In the narrowest sense of the word, it consists of a flat ...
. The projection found on these maps, dating to 1511, was stated by Snyder
in 1987 to be the same projection as Mercator's. However, given the geometry of a sundial, these maps may well have been based on the similar central cylindrical projection, a limiting case of the gnomonic projection, which is the basis for a sundial. Snyder amends his assessment to "a similar projection" in 1994.
Joseph Needham, a historian of China, wrote that the Chinese developed the Mercator projection hundreds of years before Mercator did, using it in star charts during the Song Dynasty
The Song dynasty (; ; 960–1279) was an imperial dynasty of China that began in 960 and lasted until 1279. The dynasty was founded by Emperor Taizu of Song following his usurpation of the throne of the Later Zhou. The Song conquered the rest ...
. However, this was a simple, and common, case of misidentification. The projection in use was the equirectangular projection.
Portuguese mathematician and cosmographer Pedro Nunes first described the mathematical principle of the loxodrome and its use in marine navigation. In 1537, he proposed constructing a nautical atlas composed of several large-scale sheets in the cylindrical equidistant projection as a way to minimize distortion of directions. If these sheets were brought to the same scale and assembled, they would approximate the Mercator projection.
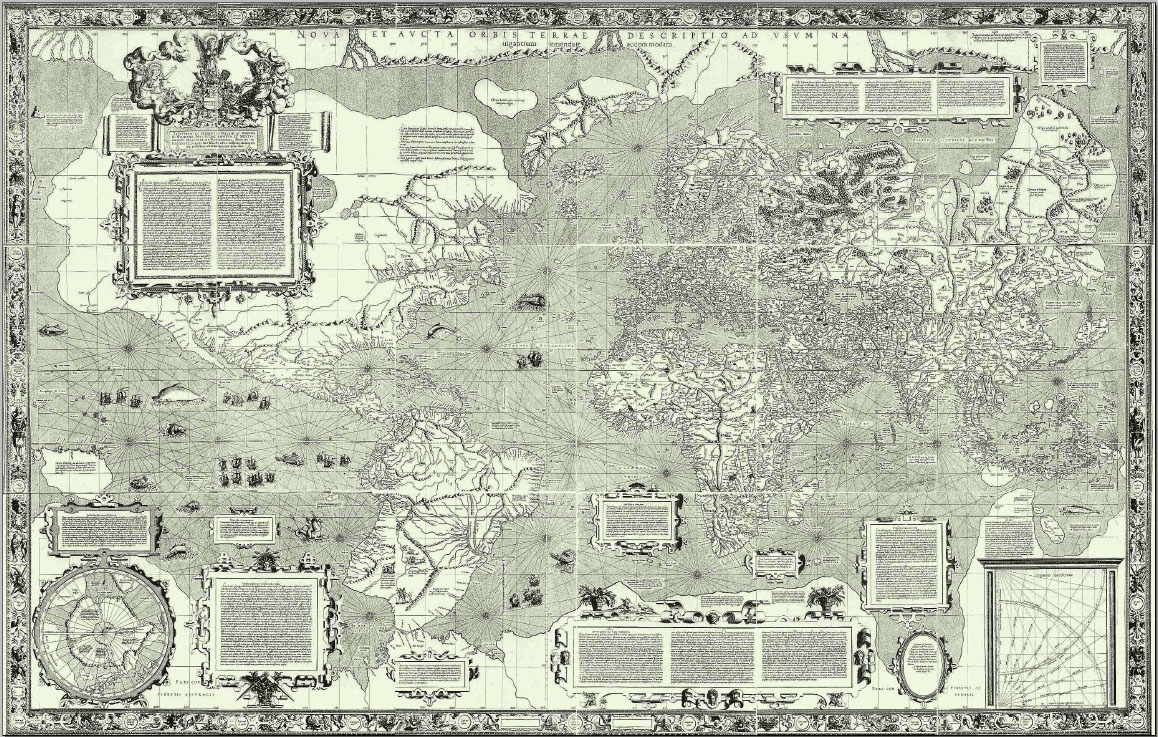
In 1569, Gerhard Kremer, known by his trade name Gerardus Mercator, announced a new projection by publishing a large planispheric map measuring and printed in eighteen separate sheets. Mercator titled the map : "A new and augmented description of Earth corrected for the use of sailors". This title, along with an elaborate explanation for using the projection that appears as a section of text on the map, shows that Mercator understood exactly what he had achieved and that he intended the projection to aid navigation. Mercator never explained the method of construction or how he arrived at it. Various hypotheses have been tendered over the years, but in any case Mercator's friendship with Pedro Nunes and his access to the loxodromic tables Nunes created likely aided his efforts.
English mathematician Edward Wright published the first accurate tables for constructing the projection in 1599 and, in more detail, in 1610, calling his treatise "Certaine Errors in Navigation". The first mathematical formulation was publicized around 1645 by a mathematician named Henry Bond (c. 1600–1678). However, the mathematics involved were developed but never published by mathematician Thomas Harriot
Thomas Harriot (; – 2 July 1621), also spelled Harriott, Hariot or Heriot, was an English astronomer, mathematician, ethnographer and translator to whom the theory of refraction is attributed. Thomas Harriot was also recognized for his con ...
starting around 1589.
The development of the Mercator projection represented a major breakthrough in the nautical cartography of the 16th century. However, it was much ahead of its time, since the old navigational and surveying techniques were not compatible with its use in navigation. Two main problems prevented its immediate application: the impossibility of determining the longitude at sea with adequate accuracy and the fact that magnetic directions, instead of geographical directions, were used in navigation. Only in the middle of the 18th century, after the marine chronometer
A marine chronometer is a precision timepiece that is carried on a ship and employed in the determination of the ship's position by celestial navigation. It is used to determine longitude by comparing Greenwich Mean Time (GMT), or in the modern ...
was invented and the spatial distribution of magnetic declination
Magnetic declination, or magnetic variation, is the angle on the horizontal plane between magnetic north (the direction the north end of a magnetized compass needle points, corresponding to the direction of the Earth's magnetic field lines) an ...
was known, could the Mercator projection be fully adopted by navigators.
Despite those position-finding limitations, the Mercator projection can be found in many world maps in the centuries following Mercator's first publication. However, it did not begin to dominate world maps until the 19th century, when the problem of position determination had been largely solved. Once the Mercator became the usual projection for commercial and educational maps, it came under persistent criticism from cartographers for its unbalanced representation of landmasses and its inability to usefully show the polar regions.
The criticisms leveled against inappropriate use of the Mercator projection resulted in a flurry of new inventions in the late 19th and early 20th century, often directly touted as alternatives to the Mercator. Due to these pressures, publishers gradually reduced their use of the projection over the course of the 20th century. However, the advent of Web mapping gave the projection an abrupt resurgence in the form of the Web Mercator projection.
Today, the Mercator can be found in marine charts, occasional world maps, and Web mapping services, but commercial atlases have largely abandoned it, and wall maps of the world can be found in many alternative projections. Google Maps
Google Maps is a web mapping platform and consumer application offered by Google. It offers satellite imagery, aerial photography, street maps, 360° interactive panoramic views of streets ( Street View), real-time traffic conditions, and rou ...
, which relied on it since 2005, still uses it for local-area maps but dropped the projection from desktop platforms in 2017 for maps that are zoomed out of local areas. Many other online mapping services still exclusively use the Web Mercator.
Properties
As in allcylindrical projections
A cylinder (from ) has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base.
A cylinder may also be defined as an infin ...
, parallels and meridians on the Mercator are straight and perpendicular to each other. In accomplishing this, the unavoidable east–west stretching of the map, which increases as distance away from the equator increases, is accompanied in the Mercator projection by a corresponding north–south stretching, so that at every point location the east–west scale is the same as the north–south scale, making it a conformal map projection
In cartography, a conformal map projection is one in which every angle between two curves that cross each other on Earth (a sphere or an ellipsoid) is preserved in the image of the projection, i.e. the projection is a conformal map in the mathema ...
. Conformal projections preserve angles around all locations.
Because the linear scale of a Mercator map increases with latitude, it distorts the size of geographical objects far from the equator and conveys a distorted perception of the overall geometry of the planet. At latitudes greater than 70° north or south the Mercator projection is practically unusable, because the linear scale
A linear scale, also called a bar scale, scale bar, graphic scale, or graphical scale, is a means of visually showing the scale of a map, nautical chart, engineering drawing, or architectural drawing. A scale bar is common element of map lay ...
becomes infinitely large at the poles. A Mercator map can therefore never fully show the polar areas (as long as the projection is based on a cylinder centered on the Earth's rotation axis; see the transverse Mercator projection
The transverse Mercator map projection (TM, TMP) is an adaptation of the standard Mercator projection. The transverse version is widely used in national and international mapping systems around the world, including the Universal Transverse Mercat ...
for another application).
The Mercator projection maps all lines with constant bearing ( rhumbs (mathematically known as loxodromes—those making constant angles with the meridians) to straight lines. The two properties, conformality and straight rhumb lines, make this projection uniquely suited to marine navigation
Navigation is a field of study that focuses on the process of monitoring and controlling the movement of a craft or vehicle from one place to another.Bowditch, 2003:799. The field of navigation includes four general categories: land navigation, ...
: courses and bearings are measured using wind roses or protractors, and the corresponding directions are easily transferred from point to point, on the map, with the help of a parallel ruler
Parallel rulers are a drafting instrument used by navigators to draw parallel lines on charts. The tool consists of two straight edges joined by two arms which allow them to move closer or further away while always remaining parallel to each oth ...
(for example).
The Mercator projection is often compared to and confused with the central cylindrical projection, which is the result of projecting points from the sphere onto a tangent cylinder along straight radial lines, as if from a light source placed at the Earth's center. Both have extreme distortion far from the equator and cannot show the poles. However, they are different projections and have different properties.
Distortion of sizes
 As on all
As on all map projection
In cartography, map projection is the term used to describe a broad set of transformations employed to represent the two-dimensional curved surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longit ...
s, shapes or sizes are distortions of the true layout of the Earth's surface.
The Mercator projection exaggerates areas far from the equator.
Examples of size distortion
*Antarctica
Antarctica () is Earth's southernmost and least-populated continent. Situated almost entirely south of the Antarctic Circle and surrounded by the Southern Ocean, it contains the geographic South Pole. Antarctica is the fifth-largest cont ...
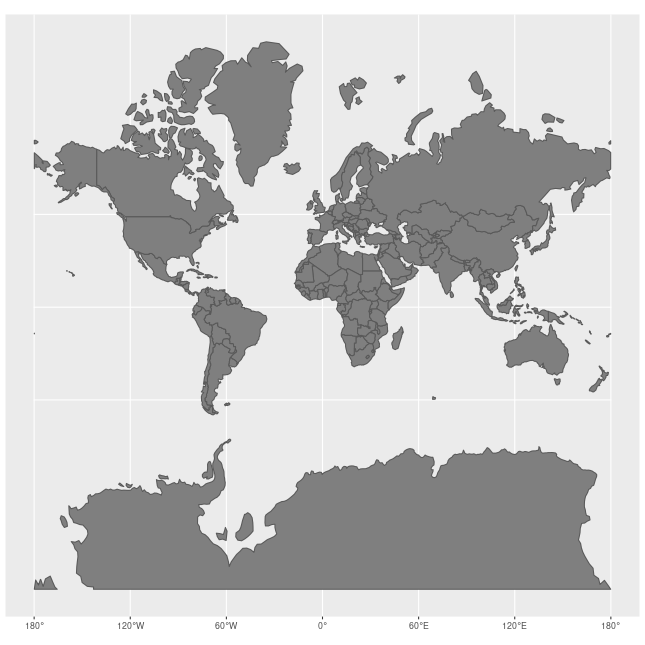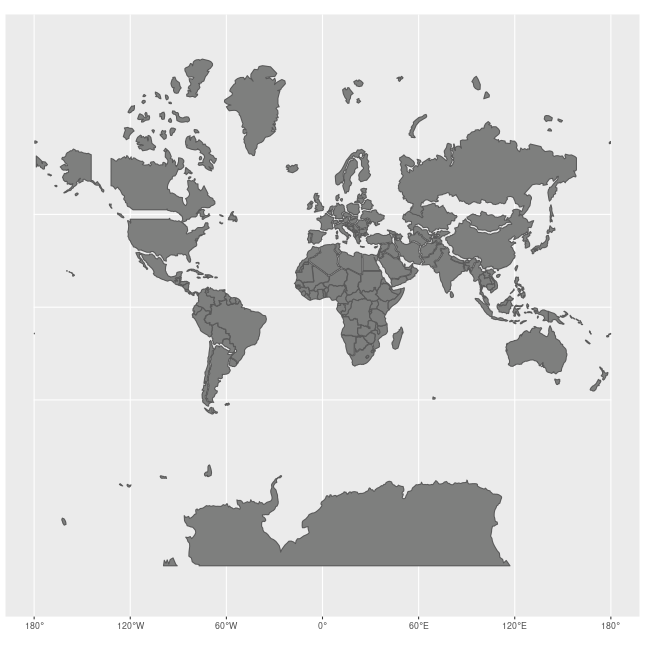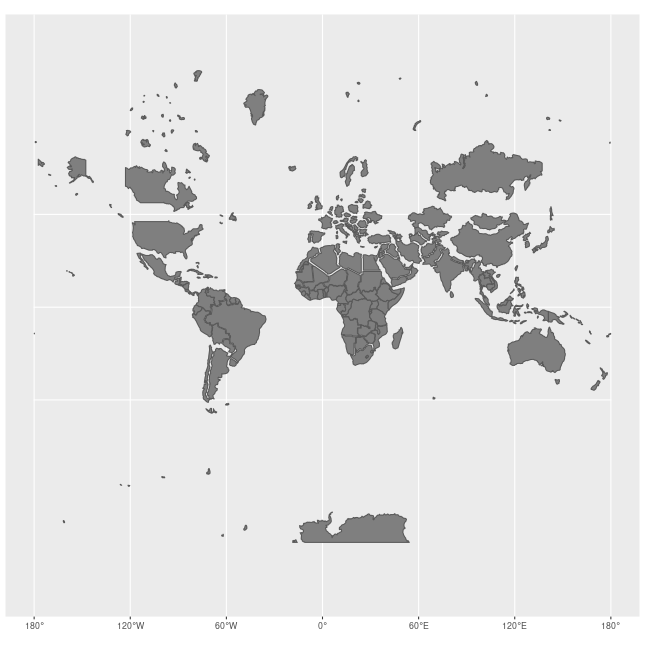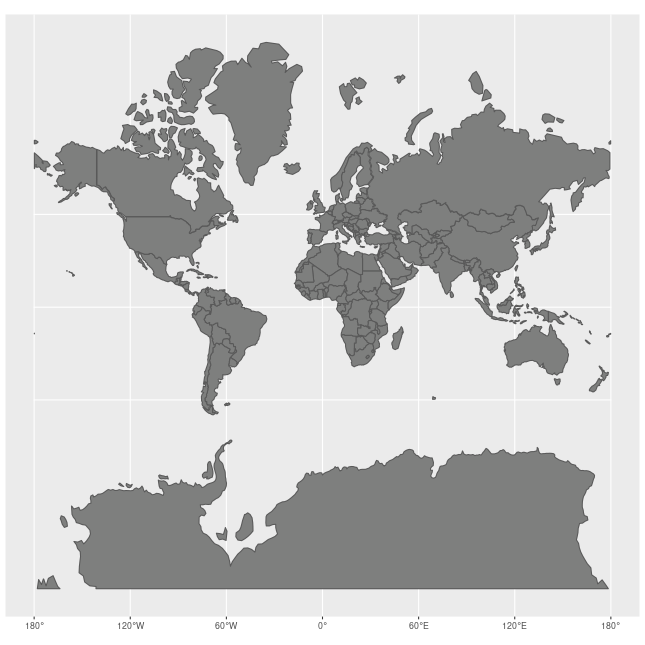
appears to be extremely large. If the entire globe were mapped, Antarctica would inflate infinitely. In reality, it is the third smallest continent.
* Ellesmere Island on the north of Canada
Canada is a country in North America. Its ten provinces and three territories extend from the Atlantic Ocean to the Pacific Ocean and northward into the Arctic Ocean, covering over , making it the world's second-largest country by tot ...
's Arctic archipelago looks about the same size as Australia, although Australia is over 39 times as large. All islands in Canada's Arctic archipelago look at least 4 times too large, and the more northern islands look even larger.
* Greenland
Greenland ( kl, Kalaallit Nunaat, ; da, Grønland, ) is an island country in North America that is part of the Kingdom of Denmark. It is located between the Arctic and Atlantic oceans, east of the Canadian Arctic Archipelago. Greenland i ...
appears the same size as Africa
Africa is the world's second-largest and second-most populous continent, after Asia in both cases. At about 30.3 million km2 (11.7 million square miles) including adjacent islands, it covers 6% of Earth's total surface area ...
, when in reality Africa's area is 14 times as large.
** Greenland's real area is comparable to the Democratic Republic of the Congo
The Democratic Republic of the Congo (french: République démocratique du Congo (RDC), colloquially "La RDC" ), informally Congo-Kinshasa, DR Congo, the DRC, the DROC, or the Congo, and formerly and also colloquially Zaire, is a country in ...
's alone.
** Africa appears to be roughly the same size as South America
South America is a continent entirely in the Western Hemisphere and mostly in the Southern Hemisphere, with a relatively small portion in the Northern Hemisphere at the northern tip of the continent. It can also be described as the sout ...
, when in reality Africa is over one and a half times as large.
* Svalbard appears to be larger than Borneo
Borneo (; id, Kalimantan) is the third-largest island in the world and the largest in Asia. At the geographic centre of Maritime Southeast Asia, in relation to major Indonesian islands, it is located north of Java, west of Sulawesi, and ea ...
, when, in reality, Borneo is about 12 times as large as Svalbard.
* Alaska
Alaska ( ; russian: Аляска, Alyaska; ale, Alax̂sxax̂; ; ems, Alas'kaaq; Yup'ik: ''Alaskaq''; tli, Anáaski) is a state located in the Western United States on the northwest extremity of North America. A semi-exclave of the U.S. ...
appears to be the same size as Australia, although Australia is actually times as large.
** Alaska also takes as much area on the map as Brazil
Brazil ( pt, Brasil; ), officially the Federative Republic of Brazil (Portuguese: ), is the largest country in both South America and Latin America. At and with over 217 million people, Brazil is the world's fifth-largest country by area ...
, whereas Brazil's area is nearly 5 times that of Alaska.
* Madagascar
Madagascar (; mg, Madagasikara, ), officially the Republic of Madagascar ( mg, Repoblikan'i Madagasikara, links=no, ; french: République de Madagascar), is an island country in the Indian Ocean, approximately off the coast of East Africa ...
and Great Britain
Great Britain is an island in the North Atlantic Ocean off the northwest coast of continental Europe. With an area of , it is the largest of the British Isles, the largest European island and the ninth-largest island in the world. It i ...
look about the same size, while Madagascar is actually more than twice as large as Great Britain.
** Sweden appears much larger than Madagascar. In reality Madagascar is a little larger.
* Russia
Russia (, , ), or the Russian Federation, is a transcontinental country spanning Eastern Europe and Northern Asia. It is the largest country in the world, with its internationally recognised territory covering , and encompassing one-eig ...
appears bigger than the whole of Africa
Africa is the world's second-largest and second-most populous continent, after Asia in both cases. At about 30.3 million km2 (11.7 million square miles) including adjacent islands, it covers 6% of Earth's total surface area ...
, or North America (without the latter's islands). It also appears twice the size of China and the contiguous United States
The United States of America (U.S.A. or USA), commonly known as the United States (U.S. or US) or America, is a country primarily located in North America. It consists of 50 states, a federal district, five major unincorporated territori ...
combined, when, in reality, the sum is comparable in size.
Criticism
Because of great land area distortions, some consider the projection unsuitable for general world maps. Mercator himself used the equal-area sinusoidal projection to show relative areas. However, despite such distortions, the Mercator projection was, especially in the late 19th and early 20th centuries, perhaps the most common projection used in world maps, despite being much criticized for this use.Kellaway, G.P. (1946). ''Map Projections'' p. 37–38. London: Methuen & Co. LTD. (According to this source, it had been claimed that the Mercator projection was used for "imperialistic motives"Abelson, C.E. (1954). ''Common Map Projections'' s. 4. Sevenoaks: W.H. Smith & Sons.Chamberlin, Wellman (1947). ''The Round Earth on Flat Paper'' s. 99. Washington, D.C.: The National Geographic Society.Fisher, Irving (1943). "A World Map on a Regular Icosahedron by Gnomonic Projection." ''Geographical Review'' 33 (4): 605. Because of its very common usage, the Mercator projection has been supposed to have influenced people's view of the world, and because it shows countries near the Equator as too small when compared to those of Europe and North America, it has been supposed to cause people to consider those countries as less important. As a result of these criticisms, modernatlas
An atlas is a collection of maps; it is typically a bundle of maps of Earth or of a region of Earth.
Atlases have traditionally been bound into book form, but today many atlases are in multimedia formats. In addition to presenting geograp ...
es no longer use the Mercator projection for world maps or for areas distant from the equator, preferring other cylindrical projection
In cartography, map projection is the term used to describe a broad set of transformations employed to represent the two-dimensional curved surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitu ...
s, or forms of equal-area projection. The Mercator projection is, however, still commonly used for areas near the equator where distortion is minimal. It is also frequently found in maps of time zones.
Arno Peters stirred controversy beginning in 1972 when he proposed what is now usually called the Gall–Peters projection to remedy the problems of the Mercator, claiming it to be his own original work without referencing prior work by cartographers such as Gall's work from 1855. The projection he promoted is a specific parameterization of the cylindrical equal-area projection. In response, a 1989 resolution by seven North American geographical groups disparaged using cylindrical projections for general-purpose world maps, which would include both the Mercator and the Gall–Peters.
Uses
Practically every marine chart in print is based on the Mercator projection due to its uniquely favorable properties for navigation. It is also commonly used by street map services hosted on the Internet, due to its uniquely favorable properties for local-area maps computed on demand. Mercator projections were also important in the mathematical development ofplate tectonics
Plate tectonics (from the la, label=Late Latin, tectonicus, from the grc, τεκτονικός, lit=pertaining to building) is the generally accepted scientific theory that considers the Earth's lithosphere to comprise a number of large ...
in the 1960s.
Marine navigation
 The Mercator projection was designed for use in marine
The Mercator projection was designed for use in marine navigation
Navigation is a field of study that focuses on the process of monitoring and controlling the movement of a craft or vehicle from one place to another.Bowditch, 2003:799. The field of navigation includes four general categories: land navigation, ...
because of its unique property of representing any course of constant bearing as a straight segment. Such a course, known as a rhumb (or, mathematically, a loxodrome) is preferred in marine navigation because ships can sail in a constant compass direction, reducing the difficult, error-prone course corrections that otherwise would be needed frequently when sailing a different course. For distances small compared to the radius of the Earth, the difference between the rhumb and the technically shortest course, a great circle segment, is negligible, and even for longer distances, the simplicity of the constant bearing makes it attractive. As observed by Mercator, on such a course, the ship would not arrive by the shortest route, but it will surely arrive. Sailing a rhumb meant that all that the sailors had to do was keep a constant course as long as they knew where they were when they started, where they intended to be when they finished, and had a map in Mercator projection that correctly showed those two coordinates.
Web Mercator
Many major online street mapping services ( Bing Maps,Google Maps
Google Maps is a web mapping platform and consumer application offered by Google. It offers satellite imagery, aerial photography, street maps, 360° interactive panoramic views of streets ( Street View), real-time traffic conditions, and rou ...
, Mapbox
Mapbox is an American provider of custom online maps for websites and applications such as Foursquare, Lonely Planet, the ''Financial Times'', The Weather Channel, Instacart Inc. and Snapchat. Since 2010, it has rapidly expanded the niche of c ...
, MapQuest
MapQuest (stylized as mapquest) is an American free online web mapping service. It was launched in 1996 as the first commercial web mapping service. MapQuest vies for market share with competitors such as Google Maps and Here.
History
MapQuest's ...
, OpenStreetMap, Yahoo! Maps
Yahoo! Maps was a free online mapping portal provided by Yahoo! Functionality included local weather powered by The Weather Channel, printing maps, and local reviews powered by Yelp. It shut down on June 30, 2015. For a time in 2019, Yahoo! Maps ...
, and others) use a variant of the Mercator projection for their map images called Web Mercator
Web Mercator, Google Web Mercator, Spherical Mercator, WGS 84 Web Mercator or WGS 84/Pseudo-Mercator is a variant of the Mercator map projection and is the de facto standard for Web mapping applications. It rose to prominence when Google Maps adop ...
or Google Web Mercator. Despite its obvious scale variation at small scales, the projection is well-suited as an interactive world map that can be zoomed seamlessly to large-scale (local) maps, where there is relatively little distortion due to the variant projection's near- conformality.
The major online street mapping services' tiling systems display most of the world at the lowest zoom level as a single square image, excluding the polar regions by truncation at latitudes of ''φ''max = ±85.05113°. (See below.) Latitude values outside this range are mapped using a different relationship that does not diverge at ''φ'' = ±90°.
Mathematics
Cylindrical projections
Although the surface of Earth is best modelled by an oblate ellipsoid of revolution, for small scale maps the ellipsoid is approximated by a sphere of radius ''a'', where ''a'' is approximately 6,371 km. This spherical approximation of Earth can be modelled by a smaller sphere of radius ''R'', called the ''globe'' in this section. The globe determines the scale of the map. The variouscylindrical projections
A cylinder (from ) has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base.
A cylinder may also be defined as an infin ...
specify how the geographic detail is transferred from the globe to a cylinder tangential to it at the equator. The cylinder is then unrolled to give the planar map. The fraction is called the representative fraction (RF) or the principal scale of the projection. For example, a Mercator map printed in a book might have an equatorial width of 13.4 cm corresponding to a globe radius of 2.13 cm and an RF of approximately (M is used as an abbreviation for 1,000,000 in writing an RF) whereas Mercator's original 1569 map has a width of 198 cm corresponding to a globe radius of 31.5 cm and an RF of about .
scale factor
In affine geometry, uniform scaling (or isotropic scaling) is a linear transformation that enlarges (increases) or shrinks (diminishes) objects by a '' scale factor'' that is the same in all directions. The result of uniform scaling is similar ...
between globe and cylinder is unity on the equator but nowhere else. In particular since the radius of a parallel, or circle of latitude, is ''R'' cos ''φ'', the corresponding parallel on the map must have been stretched by a factor of . This scale factor on the parallel is conventionally denoted by ''k'' and the corresponding scale factor on the meridian is denoted by ''h''. Snyder. Working Manual, page 20.
Scale factor
The Mercator projection is determined by the requirement that the projection be conformal. One implication of this is the "isotropy of scale factors", which means that the point scale factor is independent of direction, so that small shapes are preserved by the projection. This implies that the vertical scale factor, ''h'', equals the horizontal scale factor, ''k''. Since ''k'' = , so must ''h''.
 The classic way of showing the distortion inherent in a projection is to use Tissot's indicatrix. Nicolas Tissot noted that the scale factors at a point on a map projection, specified by the numbers ''h'' and ''k'', define an ellipse at that point. For cylindrical projections, the axes of the ellipse are aligned to the meridians and parallels. Snyder. Working Manual, page 20. For the Mercator projection, ''h'' = ''k'', so the ellipses degenerate into circles with radius proportional to the value of the scale factor for that latitude. These circles are rendered on the projected map with extreme variation in size, indicative of Mercator's scale variations.
The classic way of showing the distortion inherent in a projection is to use Tissot's indicatrix. Nicolas Tissot noted that the scale factors at a point on a map projection, specified by the numbers ''h'' and ''k'', define an ellipse at that point. For cylindrical projections, the axes of the ellipse are aligned to the meridians and parallels. Snyder. Working Manual, page 20. For the Mercator projection, ''h'' = ''k'', so the ellipses degenerate into circles with radius proportional to the value of the scale factor for that latitude. These circles are rendered on the projected map with extreme variation in size, indicative of Mercator's scale variations.
Mercator projection transformations
Derivation
As discussed above, the isotropy condition implies that ''h'' = ''k'' = . Consider a point on the globe of radius ''R'' with longitude ''λ'' and latitude ''φ''. If ''φ'' is increased by an infinitesimal amount, ''dφ'', the point moves ''R'' ''dφ'' along a meridian of the globe of radius ''R'', so the corresponding change in ''y'', ''dy'', must be ''hR'' ''dφ'' = ''R'' sec ''φ'' ''dφ''. Therefore ''y′''(''φ'') = ''R'' sec ''φ''. Similarly, increasing ''λ'' by ''dλ'' moves the point ''R'' cos ''φ'' ''dλ'' along a parallel of the globe, so ''dx'' = ''kR'' cos ''φ'' ''dλ'' = ''R'' ''dλ''. That is, ''x′''(''λ'') = ''R''. Integrating the equations : with ''x''(''λ''0) = 0 and ''y''(0) = 0, gives ''x(λ)'' and ''y(φ)''. The value ''λ''0 is the longitude of an arbitrary central meridian that is usually, but not always, that of Greenwich (i.e., zero). The angles ''λ'' and ''φ'' are expressed in radians. By the integral of the secant function, NIST. See Section4.26#ii
an
4.23#viii
/ref>
Inverse transformations
: The expression on the right of the second equation defines theGudermannian function
In mathematics, the Gudermannian function relates a hyperbolic angle measure \psi to a circular angle measure \phi called the ''gudermannian'' of \psi and denoted \operatorname\psi. The Gudermannian function reveals a close relationship betwee ...
; i.e., ''φ'' = gd(): the direct equation may therefore be written as ''y'' = ''R''·gd−1(''φ'').
Alternative expressions
There are many alternative expressions for ''y''(''φ''), all derived by elementary manipulations. : Corresponding inverses are: : For angles expressed in degrees: : The above formulae are written in terms of the globe radius ''R''. It is often convenient to work directly with the map width ''W'' = 2''R''. For example, the basic transformation equations become :Truncation and aspect ratio
The ordinate ''y'' of the Mercator projection becomes infinite at the poles and the map must be truncated at some latitude less than ninety degrees. This need not be done symmetrically. Mercator's original map is truncated at 80°N and 66°S with the result that European countries were moved toward the centre of the map. The aspect ratio of his map is = 1.65. Even more extreme truncations have been used: a Finnish school atlas was truncated at approximately 76°N and 56°S, an aspect ratio of 1.97. Much Web-based mapping uses a zoomable version of the Mercator projection with an aspect ratio of one. In this case the maximum latitude attained must correspond to ''y'' = ±, or equivalently = . Any of the inverse transformation formulae may be used to calculate the corresponding latitudes: :Small element geometry
The relations between ''y''(''φ'') and properties of the projection, such as the transformation of angles and the variation in scale, follow from the geometry of corresponding ''small'' elements on the globe and map. The figure below shows a point P at latitude ''φ'' and longitude ''λ'' on the globe and a nearby point Q at latitude ''φ'' + ''δφ'' and longitude ''λ'' + ''δλ''. The vertical lines PK and MQ are arcs of meridians of length ''Rδφ''. The horizontal lines PM and KQ are arcs of parallels of length ''R''(cos ''φ'')''δλ''. The corresponding points on the projection define a rectangle of width ''δx'' and height ''δy''.Formulae for distance
Converting ruler distance on the Mercator map into true ( great circle) distance on the sphere is straightforward along the equator but nowhere else. One problem is the variation of scale with latitude, and another is that straight lines on the map ( rhumb lines), other than the meridians or the equator, do not correspond to great circles. The distinction between rhumb (sailing) distance and great circle (true) distance was clearly understood by Mercator. (See Legend 12 on the 1569 map.) He stressed that the rhumb line distance is an acceptable approximation for true great circle distance for courses of short or moderate distance, particularly at lower latitudes. He even quantifies his statement: "When the great circle distances which are to be measured in the vicinity of the equator do not exceed 20 degrees of a great circle, or 15 degrees near Spain and France, or 8 and even 10 degrees in northern parts it is convenient to use rhumb line distances". For a ruler measurement of a ''short'' line, with midpoint at latitude ''φ'', where the scale factor is ''k'' = sec ''φ'' = : :True distance = rhumb distance ≅ ruler distance × cos ''φ'' / RF. (short lines) With radius and great circle circumference equal to 6,371 km and 40,030 km respectively an RF of , for which ''R'' = 2.12 cm and ''W'' = 13.34 cm, implies that a ruler measurement of 3 mm. in any direction from a point on the equator corresponds to approximately 900 km. The corresponding distances for latitudes 20°, 40°, 60° and 80° are 846 km, 689 km, 450 km and 156 km respectively. Longer distances require various approaches.On the equator
Scale is unity on the equator (for a non-secant projection). Therefore, interpreting ruler measurements on the equator is simple: :True distance = ruler distance / RF (equator) For the above model, with RF = , 1 cm corresponds to 3,000 km.On other parallels
On any other parallel the scale factor is sec ''φ'' so that :Parallel distance = ruler distance × cos ''φ'' / RF (parallel). For the above model 1 cm corresponds to 1,500 km at a latitude of 60°. This is not the shortest distance between the chosen endpoints on the parallel because a parallel is not a great circle. The difference is small for short distances but increases as ''λ'', the longitudinal separation, increases. For two points, A and B, separated by 10° of longitude on the parallel at 60° the distance along the parallel is approximately 0.5 km greater than the great circle distance. (The distance AB along the parallel is (''a'' cos ''φ'') ''λ''. The length of the chord AB is 2(''a'' cos ''φ'') sin . This chord subtends an angle at the centre equal to 2arcsin(cos ''φ'' sin ) and the great circle distance between A and B is 2''a'' arcsin(cos ''φ'' sin ).) In the extreme case where the longitudinal separation is 180°, the distance along the parallel is one half of the circumference of that parallel; i.e., 10,007.5 km. On the other hand, the geodesic between these points is a great circle arc through the pole subtending an angle of 60° at the center: the length of this arc is one sixth of the great circle circumference, about 6,672 km. The difference is 3,338 km so the ruler distance measured from the map is quite misleading even after correcting for the latitude variation of the scale factor.On a meridian
A meridian of the map is a great circle on the globe but the continuous scale variation means ruler measurement alone cannot yield the true distance between distant points on the meridian. However, if the map is marked with an accurate and finely spaced latitude scale from which the latitude may be read directly—as is the case for theMercator 1569 world map
The Mercator world map of 1569 is titled (Renaissance Latin for "New and more complete representation of the terrestrial globe properly adapted for use in navigation"). The title shows that Gerardus Mercator aimed to present contemporary know ...
(sheets 3, 9, 15) and all subsequent nautical charts—the meridian distance between two latitudes ''φ''1 and ''φ''2 is simply
:
If the latitudes of the end points cannot be determined with confidence then they can be found instead by calculation on the ruler distance. Calling the ruler distances of the end points on the map meridian as measured from the equator ''y''1 and ''y''2, the true distance between these points on the sphere is given by using any one of the inverse Mercator formulæ:
:
where ''R'' may be calculated from the width ''W'' of the map by ''R'' = . For example, on a map with ''R'' = 1 the values of ''y'' = 0, 1, 2, 3 correspond to latitudes of ''φ'' = 0°, 50°, 75°, 84° and therefore the successive intervals of 1 cm on the map correspond to latitude intervals on the globe of 50°, 25°, 9° and distances of 5,560 km, 2,780 km, and 1,000 km on the Earth.
On a rhumb
A straight line on the Mercator map at angle ''α'' to the meridians is a rhumb line. When ''α'' = or the rhumb corresponds to one of the parallels; only one, the equator, is a great circle. When ''α'' = 0 or it corresponds to a meridian great circle (if continued around the Earth). For all other values it is a spiral from pole to pole on the globe intersecting all meridians at the same angle, and is thus not a great circle. This section discusses only the last of these cases. If ''α'' is neither 0 nor then the above figure of the infinitesimal elements shows that the length of an infinitesimal rhumb line on the sphere between latitudes ''φ''; and ''φ'' + ''δφ'' is ''a'' sec ''α'' ''δφ''. Since ''α'' is constant on the rhumb this expression can be integrated to give, for finite rhumb lines on the Earth: : Once again, if Δ''φ'' may be read directly from an accurate latitude scale on the map, then the rhumb distance between map points with latitudes ''φ''1 and ''φ''2 is given by the above. If there is no such scale then the ruler distances between the end points and the equator, ''y''1 and ''y''2, give the result via an inverse formula: : These formulæ give rhumb distances on the sphere which may differ greatly from true distances whose determination requires more sophisticated calculations.Generalization to the ellipsoid
When the Earth is modelled by aspheroid
A spheroid, also known as an ellipsoid of revolution or rotational ellipsoid, is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters. A spheroid has ...
( ellipsoid of revolution) the Mercator projection must be modified if it is to remain conformal. The transformation equations and scale factor for the non-secant version are
The scale factor is unity on the equator, as it must be since the cylinder is tangential to the ellipsoid at the equator. The ellipsoidal correction of the scale factor increases with latitude but it is never greater than ''e''2, a correction of less than 1%. (The value of ''e''2 is about 0.006 for all reference ellipsoids.) This is much smaller than the scale inaccuracy, except very close to the equator. Only accurate Mercator projections of regions near the equator will necessitate the ellipsoidal corrections.
The inverse is solved iteratively, as the isometric latitude is involved.
See also
*Cartography
Cartography (; from grc, χάρτης , "papyrus, sheet of paper, map"; and , "write") is the study and practice of making and using maps. Combining science, aesthetics and technique, cartography builds on the premise that reality (or an i ...
* Central cylindrical projection – more distorted; sometimes erroneously described as the method of construction of the Mercator projection
*Conformal map projection
In cartography, a conformal map projection is one in which every angle between two curves that cross each other on Earth (a sphere or an ellipsoid) is preserved in the image of the projection, i.e. the projection is a conformal map in the mathema ...
* Equirectangular projection – less distorted, but not equal-area
* Gall–Peters projection – an equal-area cylindrical projection
* Jordan Transverse Mercator
* List of map projections
*Mercator 1569 world map
The Mercator world map of 1569 is titled (Renaissance Latin for "New and more complete representation of the terrestrial globe properly adapted for use in navigation"). The title shows that Gerardus Mercator aimed to present contemporary know ...
*Nautical chart
A nautical chart is a graphic representation of a sea area and adjacent coastal regions. Depending on the scale of the chart, it may show depths of water and heights of land ( topographic map), natural features of the seabed, details of the co ...
* Rhumbline network
* Tissot's indicatrix
*Transverse Mercator projection
The transverse Mercator map projection (TM, TMP) is an adaptation of the standard Mercator projection. The transverse version is widely used in national and international mapping systems around the world, including the Universal Transverse Mercat ...
*Universal Transverse Mercator coordinate system
The Universal Transverse Mercator (UTM) is a map projection system for assigning coordinates to locations on the surface of the Earth. Like the traditional method of latitude and longitude, it is a horizontal position representation, which means i ...
Notes
References
Bibliography
*. * * * * * This paper can be downloaded froUSGS pages.
It gives full details of most projections, together with interesting introductory sections, but it does not derive any of the projections from first principles.
Further reading
*External links
– contains high-resolution images of the 1569 world map by Mercator.
Table of examples and properties of all common projections
from radicalcartography.net.
* ttp://www.hydrometronics.com/downloads/Web%20Mercator%20-%20Non-Conformal,%20Non-Mercator%20(notes).pdf Web Mercator: Non-Conformal, Non-Mercator (Noel Zinn, Hydrometronics LLC)br>Mercator's Projection at University of British Columbia
{{Authority control Conformal projections Map projections 16th-century inventions Early modern Netherlandish cartography