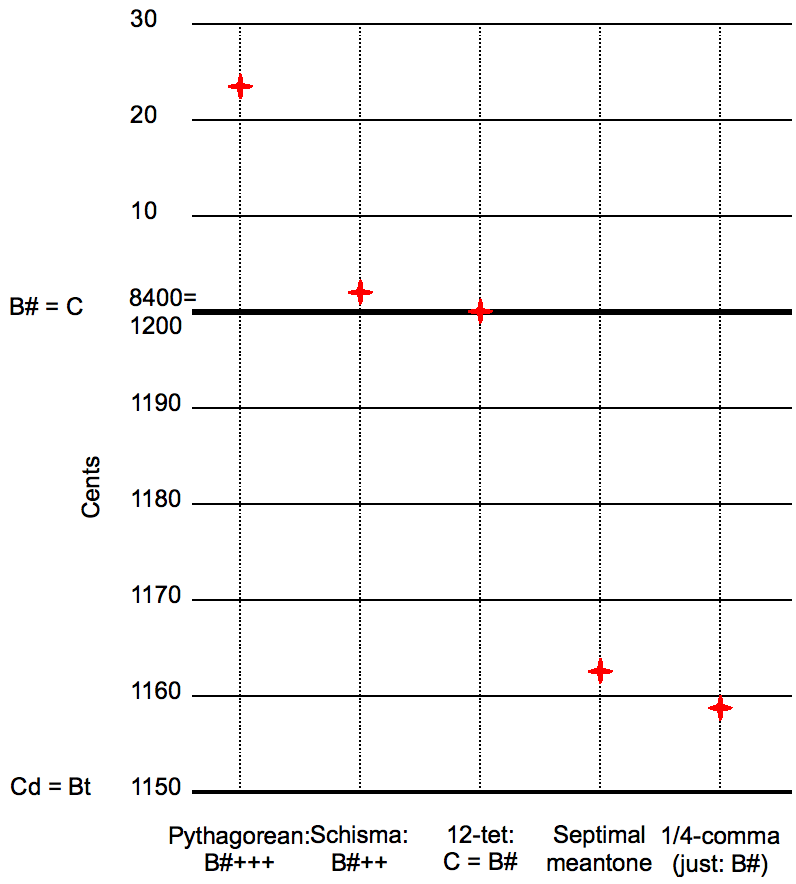musical tuning In music, there are two common meanings for tuning: * Tuning practice, the act of tuning an instrument or voice. * Tuning systems, the various systems of pitches used to tune an instrument, and their theoretical bases. Tuning practice Tuni ...

, a temperament is a tuning system that slightly compromises the pure intervals of

just intonation In music, just intonation or pure intonation is the tuning of musical intervals as whole number ratios (such as 3:2 or 4:3) of frequencies. An interval tuned in this way is said to be pure, and is called a just interval. Just intervals (and ...

to meet other requirements. Most modern Western musical instruments are tuned in the

equal temperament An equal temperament is a musical temperament or tuning system, which approximates just intervals by dividing an octave (or other interval) into equal steps. This means the ratio of the frequencies of any adjacent pair of notes is the same, ...

system. Tempering is the process of altering the size of an interval by making it narrower or wider than pure. "Any plan that describes the adjustments to the sizes of some or all of the twelve fifth intervals in the

circle of fifths In music theory, the circle of fifths is a way of organizing the 12 chromatic pitches as a sequence of perfect fifths. (This is strictly true in the standard 12-tone equal temperament system — using a different system requires one interval of ...

so that they accommodate pure

octave In music, an octave ( la, octavus: eighth) or perfect octave (sometimes called the diapason) is the interval between one musical pitch and another with double its frequency. The octave relationship is a natural phenomenon that has been refer ...

s and produce certain sizes of

major third In classical music, a third is a musical interval encompassing three staff positions (see Interval number for more details), and the major third () is a third spanning four semitones. Forte, Allen (1979). ''Tonal Harmony in Concept and P ...

s is called a ''temperament''." Temperament is especially important for keyboard instruments, which typically allow a player to play only the pitches assigned to the various keys, and lack any way to alter pitch of a note in performance. Historically, the use of

Pythagorean tuning Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2.Bruce Benward and Marilyn Nadine Saker (2003). ''Music: In Theory and Practice'', seventh edition, 2 vols. (Boston: M ...

and meantone temperament meant that such instruments could sound "in tune" in one key, or some keys, but would then have more dissonance in other keys. In the words of William Hubbard's ''Musical Dictionary'' (1908), an anomalous chord is a "chord containing an interval" that "has been made very sharp or flat in tempering the scale for instruments of fixed pitches". The development of well temperament allowed fixed-pitch instruments to play reasonably well in all of the keys. The famous '' Well-Tempered Clavier'' by

Johann Sebastian Bach Johann Sebastian Bach (28 July 1750) was a German composer and musician of the late Baroque period. He is known for his orchestral music such as the ''Brandenburg Concertos''; instrumental compositions such as the Cello Suites; keyboard wo ...

takes full advantage of this breakthrough, with pieces written in all 24 major and minor keys. However, while unpleasant intervals (such as the

wolf interval In music theory, the wolf fifth (sometimes also called Procrustean fifth, or imperfect fifth) Paul, Oscar (1885). A manual of harmony for use in music-schools and seminaries and for self-instruction', p.165. Theodore Baker, trans. G. Schirmer ...

) were avoided, the sizes of intervals were still not consistent between keys, and so each key still had its own character. This variation led in the 18th century to an increase in the use of

, in which the frequency ratio between each pair of adjacent notes on the keyboard was made equal, allowing music to be transposed between keys without changing the relationship between notes.

Definition

"''Temperament'' refers to the various tuning systems for the subdivision of the octave," the four principal tuning systems being Pythagorean tuning, just intonation, mean-tone temperament, and equal temperament.Cooper, Paul (1975). ''Perspectives in Music Theory'', p.16. Dodd, Mead & Co. . In ''just intonation'', every interval between two pitches corresponds to a whole number

ratio In mathematics, a ratio shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ...

between their

frequencies Frequency is the number of occurrences of a repeating event per unit of time. It is also occasionally referred to as ''temporal frequency'' for clarity, and is distinct from '' angular frequency''. Frequency is measured in hertz (Hz) which is e ...

, allowing intervals varying from the highest consonance to highly dissonant. For instance, 660 Hz / 440 Hz (a ratio of 3:2) constitutes a fifth, and 880 Hz / 440 Hz (2:1) an octave. Such intervals (termed "just") have a stability, or purity to their sound, when played simultaneously (assuming they are played using timbres with harmonic partials). If one of those pitches is adjusted slightly to deviate from the just interval, a trained ear can detect this change by the presence of '' beats'', which are periodical oscillations in the note's intensity. If, for example, two sound signals with frequencies that vary just by 0.5 Hz are played simultaneously, both signals are out of phase by a very small margin, creating the periodical oscillations in the intensity of the final sound (caused by the superposition of both signals) with a repetition period of 2 seconds (following the equation ''Tr=1/Δf'', ''Tr'' being the period of repetition and ''Δf'' being the difference in frequencies between both signals), because the amplitude of the signals is only in phase, and therefore has a maximum superposition value, once every period of repetition.

Acoustic physics

When a musical instrument with harmonic overtones is played, the ear hears a composite waveform that includes a fundamental frequency (e.g., 440 Hz) and those overtones (880 Hz, 1320 Hz, 1760 Hz, etc.)—a series of just intervals. The waveform of such a tone (as pictured on an oscilloscope) is characterized by a shape that is complex compared to a simple (sine) waveform, but remains periodic. When two tones depart from exact integer ratios, the shape waveform becomes erratic—a phenomenon that may be described as destabilization. As the composite waveform becomes more erratic, the consonance of the interval also changes.

Temperament in music

Tempering an interval involves the deliberate use of such minor adjustments (accepting the related destabilization) to enable musical possibilities that are impractical using just intonation. The most widely known example of this is the use of equal temperament to address problems of older temperaments, allowing for consistent tuning of keyboard and fretted instruments and enabling musical composition in, and modulation among, the various keys.

Meantone temperament

Before Meantone temperament became widely used in the

Renaissance The Renaissance ( , ) , from , with the same meanings. is a period in European history marking the transition from the Middle Ages to modernity and covering the 15th and 16th centuries, characterized by an effort to revive and surpass id ...

, the most commonly used tuning system was

. Pythagorean tuning was a system of just intonation that tuned every note in a scale from a progression of pure

perfect fifth In music theory, a perfect fifth is the musical interval corresponding to a pair of pitches with a frequency ratio of 3:2, or very nearly so. In classical music from Western culture, a fifth is the interval from the first to the last of five ...

s. This was quite suitable for much of the harmonic practice until then (''See:

Quartal harmony In music, quartal harmony is the building of harmonic structures built from the intervals of the perfect fourth, the augmented fourth and the diminished fourth. For instance, a three-note quartal chord on C can be built by stacking perfect four ...

''), but in the Renaissance, musicians wished to make much more use of

Tertian harmony In music theory, ''tertian'' ( la, tertianus, "of or concerning thirds") describes any piece, chord, counterpoint etc. constructed from the intervals of (major and minor) thirds. An interval such as that between the notes A and C encompasses 3 ...

. The

of Pythagorean tuning differed from a just major third by an amount known as

syntonic comma In music theory, the syntonic comma, also known as the chromatic diesis, the Didymean comma, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80 (= 1.0125 ...

, which musicians of the time found annoying. Their solution, laid out by Pietro Aron in the early 16th century, and referred to as meantone temperament (or quarter-comma meantone temperament), was to ''temper'' the interval of a perfect fifth slightly narrower than in just intonation, and then proceed much like Pythagorean tuning, but using this tempered fifth instead of the just one. With the correct amount of tempering, the syntonic comma is removed from its major thirds, making them just. This compromise, however, leaves all fifths in this tuning system with a slight beating. However, because a sequence of four fifths makes up one third, this beating effect on the fifths is only one quarter as strong as the beating effect on the thirds of Pythagorean tuning, which is why it was considered a very acceptable compromise by Renaissance musicians. Pythagorean tuning also had a second problem, which meantone temperament does not solve, which is the problem of

modulation In electronics and telecommunications, modulation is the process of varying one or more properties of a periodic waveform, called the '' carrier signal'', with a separate signal called the ''modulation signal'' that typically contains informat ...

(''see

below Below may refer to: *Earth * Ground (disambiguation) * Soil * Floor * Bottom (disambiguation) * Less than *Temperatures below freezing * Hell or underworld People with the surname * Ernst von Below (1863–1955), German World War I general * Fr ...

''), which is restricted because both have a broken

. A series of 12 just fifths as in Pythagorean tuning does not return to the original pitch, but rather differs by a

Pythagorean comma In musical tuning, the Pythagorean comma (or ditonic comma), named after the ancient mathematician and philosopher Pythagoras, is the small interval (or comma) existing in Pythagorean tuning between two enharmonically equivalent notes such as ...

, which makes that tonal area of the system more or less unusable. In meantone temperament, this effect is even more pronounced (the fifth over the break in the circle is known as the

Wolf interval In music theory, the wolf fifth (sometimes also called Procrustean fifth, or imperfect fifth) Paul, Oscar (1885). A manual of harmony for use in music-schools and seminaries and for self-instruction', p.165. Theodore Baker, trans. G. Schirmer ...

, as its intense beating was likened to a "howling"). The use of

53 equal temperament In music, 53 equal temperament, called 53 TET, 53 EDO, or 53 ET, is the tempered scale derived by dividing the octave into 53 equal steps (equal frequency ratios). Each step represents a frequency ratio of 2, or 22.6415& ...

provides a solution for the Pythagorean tuning, and

31 equal temperament In music, 31 equal temperament, 31-ET, which can also be abbreviated 31-TET (31 tone ET) or 31-EDO (equal division of the octave), also known as tricesimoprimal, is the tempered scale derived by dividing the octave into 31 equal-sized steps (equa ...

for the Meantone.

Well temperament and equal temperament

Just intonation has the problem that it cannot modulate to a different key (a very common means of expression throughout the

common practice period In European art music, the common-practice period is the era of the tonal system. Most of its features persisted from the mid-Baroque period through the Classical and Romantic periods, roughly from 1650 to 1900. There was much stylistic evoluti ...

of music) without discarding many of the tones used in the previous key, thus for every key to which the musician wishes to modulate, the instrument must provide a few more

string String or strings may refer to: *String (structure), a long flexible structure made from threads twisted together, which is used to tie, bind, or hang other objects Arts, entertainment, and media Films * ''Strings'' (1991 film), a Canadian anim ...

fret A fret is any of the thin strips of material, usually metal wire, inserted laterally at specific positions along the neck or fretboard of a stringed instrument. Frets usually extend across the full width of the neck. On some historical instru ...

s, or holes for him or her to use. When building an instrument, this can be very impractical. Well temperament is the name given to a variety of different systems of temperament that were employed to solve this problem, in which some keys are more in tune than others, but all can be used. This phenomenon gives rise to infinite shades of key-colors, which are lost in the modern standard version: 12-tone equal temperament (12-TET). Unlike meantone temperament, which alters the fifth to "temper out" the syntonic comma, 12-TET tempers out the

, thus creating a cycle of fifths that repeats itself exactly after 12 steps. This allowed the intervals of

tertian harmony In music theory, ''tertian'' ( la, tertianus, "of or concerning thirds") describes any piece, chord, counterpoint etc. constructed from the intervals of (major and minor) thirds. An interval such as that between the notes A and C encompasses 3 ...

, thirds and fifths, to be fairly close to their just counterparts (the fifths almost imperceptibly beating, the thirds a little milder than the syntonic beating of Pythagorean tuning), while permitting the freedom to modulate to any key and by various means (e.g. ''common-tone'' and ''enharmonic'' modulation, ''see

''). This freedom of modulation also allowed substantial use of more distant harmonic relationships, such as the

Neapolitan chord In Classical music theory, a Neapolitan chord (or simply a "Neapolitan") is a major chord built on the lowered ( flatted) second (supertonic) scale degree. In Schenkerian analysis, it is known as a Phrygian II, since in minor scales the chord is ...

, which became very important to

Romantic Romantic may refer to: Genres and eras * The Romantic era, an artistic, literary, musical and intellectual movement of the 18th and 19th centuries ** Romantic music, of that era ** Romantic poetry, of that era ** Romanticism in science, of that e ...

composers in the 19th century.

Frequently used equal temperament scales

Notes

:1.The cited reference here has "chroniatic", an obvious misprint.

References

External links

Articles

''The Wolf at Our Heels: The centuries-old struggle to play in tune'', by Jan Swafford, 2010-04-20
* Willem Kroesbergen, Andrew Cruickshank:
18th century quotes on J.S. Bach's temperament
*Dominic Eckersley:
Rosetta Revisited: Bach's Very Ordinary Temperament
. Academia website.

Books

(mathematical perspective with two chapters on temperament) by Dave Benson
''Tuning And Temperament A Historical Survey''
(1951) by J. Murray Barbour
Essay on Musical Temperamentpart 2
by Prof. Fisher (Yale College)
"Temperament" from ''A supplement to Mr. Chambers's cyclopædia'' (1753)''Theory and practice of just intonation'' (1850)
by Thomas Perronet Thompson
''Elements of musical composition: comprehending the rules of thorough bass and the theory of tuning''
(1812) by William Crotch
''An essay on temperament''
(1832) by J. Jousse
''Essay on musical intervals, harmonics, and the temperament of the musical scale, &c''
(1835) by Wesley Stoker B. Woolhouse
Harmonics, or The philosophy of musical sounds (1759)
by Robert Smith (1689–1768)
Modern organ tuning : the how and why?
by Hermann Smith (1824–1910)
Piano Tuning: A Simple and Accurate Method for Amateurs
by Jerry Cree Fischer
The organ viewed from within : a practical handbook on the mechanism of the organ, with a chapter on tuning
by John Broadhouse
Construction, Tuning and Care of the Piano-forte (1887)
by Edward Quincy Norton
Regulation and Repair of Piano and Player Mechanism, Together with Tuning as Science and Art (1909)
by William Braid White
Modern piano tuning and allied arts (1917)
by William Braid White (1878–1959) * {{Authority control