Multi-stage Game on:
[Wikipedia]
[Google]
[Amazon]
In
The payoff to each player is the simple sum of the payoffs of both games.
Players cannot observe the action of the other player within a round; however, at the beginning of Round 2, Player 2 finds out about Player 1's action in Round 1, while Player 1 does not find out about Player 2's action in Round 1.
For Player 1, there are strategies.
For Player 2, there are strategies.
The extensive form of this multi-stage game is shown in ''Figure 2'':
In this game, the only Nash Equilibrium in each stage is (B, b).
(BB, bb) will be the Nash Equilibrium for the entire game.
The payoff to each player is the simple sum of the payoffs of both games.
Players cannot observe the action of the other player within a round; however, at the beginning of Round 2, both players find out about the other's action in Round 1.
For Player 1, there are strategies.
For Player 2, there are strategies.
The extensive form of this multi-stage game is shown in ''Figure 5'':
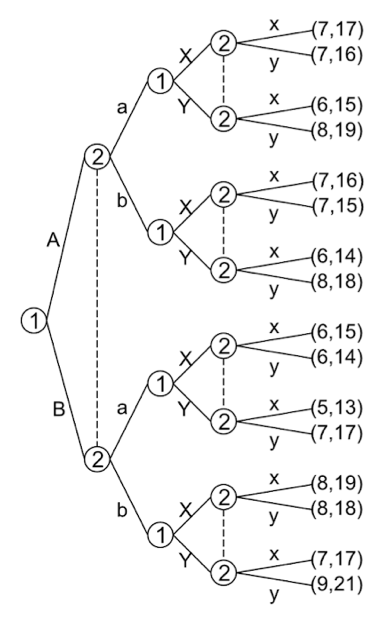Each of the two stages has two Nash Equilibria: which are (A, a), (B, b), (X, x), and (Y, y).
If the complete contingent strategy of Player 1 matches Player 2 (i.e. AXXXX, axxxx), it will be a Nash Equilibrium. There are 32 such combinations in this multi-stage game. Additionally, all of these equilibria are subgame-perfect.
game theory
Game theory is the study of mathematical models of strategic interactions. It has applications in many fields of social science, and is used extensively in economics, logic, systems science and computer science. Initially, game theory addressed ...
, a multi-stage game is a sequence of several simultaneous game
In game theory, a simultaneous game or static game is a game where each player chooses their action without knowledge of the actions chosen by other players. Simultaneous games contrast with sequential games, which are played by the players taki ...
s played one after the other. This is a generalization of a repeated game
In game theory, a repeated game (or iterated game) is an extensive form game that consists of a number of repetitions of some base game (called a stage game). The stage game is usually one of the well-studied 2-person games. Repeated games capt ...
: a repeated game is a special case of a multi-stage game, in which the stage games are identical.
Multi-Stage Game with Different Information Sets
As an example, consider a two-stage game in which the stage game in ''Figure 1'' is played in each of two periods:
The payoff to each player is the simple sum of the payoffs of both games.
Players cannot observe the action of the other player within a round; however, at the beginning of Round 2, Player 2 finds out about Player 1's action in Round 1, while Player 1 does not find out about Player 2's action in Round 1.
For Player 1, there are strategies.
For Player 2, there are strategies.
The extensive form of this multi-stage game is shown in ''Figure 2'':
In this game, the only Nash Equilibrium in each stage is (B, b).
(BB, bb) will be the Nash Equilibrium for the entire game.
Multi-Stage Game with Changing Payoffs
In this example, consider a two-stage game in which the stage game in ''Figure 3'' is played in the first period and the game in ''Figure 4'' is played in the second:
The payoff to each player is the simple sum of the payoffs of both games.
Players cannot observe the action of the other player within a round; however, at the beginning of Round 2, both players find out about the other's action in Round 1.
For Player 1, there are strategies.
For Player 2, there are strategies.
The extensive form of this multi-stage game is shown in ''Figure 5'':
Each of the two stages has two Nash Equilibria: which are (A, a), (B, b), (X, x), and (Y, y).
If the complete contingent strategy of Player 1 matches Player 2 (i.e. AXXXX, axxxx), it will be a Nash Equilibrium. There are 32 such combinations in this multi-stage game. Additionally, all of these equilibria are subgame-perfect.
References
* * Game theory game classes {{gametheory-stub