Multi-objective Optimization on:
[Wikipedia]
[Google]
[Amazon]
Multi-objective optimization or Pareto optimization (also known as multi-objective programming, vector optimization, multicriteria optimization, or multiattribute optimization) is an area of multiple-criteria decision making that is concerned with mathematical optimization problems involving more than one
 If some objective function is to be maximized, it is equivalent to minimize its negative or its inverse. We denote the image of ; a feasible solution or feasible decision; and an objective vector or an outcome.
In multi-objective optimization, there does not typically exist a feasible solution that minimizes all objective functions simultaneously. Therefore, attention is paid to Pareto optimal solutions; that is, solutions that cannot be improved in any of the objectives without degrading at least one of the other objectives. In mathematical terms, a feasible solution is said to (Pareto) dominate another solution , if
#, and
#.
A solution (and the corresponding outcome ) is called Pareto optimal if there does not exist another solution that dominates it. The set of Pareto optimal outcomes, denoted , is often called the Pareto front, Pareto frontier, or Pareto boundary.
The Pareto front of a multi-objective optimization problem is bounded by a so-called
If some objective function is to be maximized, it is equivalent to minimize its negative or its inverse. We denote the image of ; a feasible solution or feasible decision; and an objective vector or an outcome.
In multi-objective optimization, there does not typically exist a feasible solution that minimizes all objective functions simultaneously. Therefore, attention is paid to Pareto optimal solutions; that is, solutions that cannot be improved in any of the objectives without degrading at least one of the other objectives. In mathematical terms, a feasible solution is said to (Pareto) dominate another solution , if
#, and
#.
A solution (and the corresponding outcome ) is called Pareto optimal if there does not exist another solution that dominates it. The set of Pareto optimal outcomes, denoted , is often called the Pareto front, Pareto frontier, or Pareto boundary.
The Pareto front of a multi-objective optimization problem is bounded by a so-called
Optimal Resource Allocation in Coordinated Multi-Cell Systems
Foundations and Trends in Communications and Information Theory, vol. 9, no. 2-3, pp. 113-381, 2013. The main resources are time intervals, frequency blocks, and transmit powers. Each user has its own objective function that, for example, can represent some combination of the data rate, latency, and energy efficiency. These objectives are conflicting since the frequency resources are very scarce, thus there is a need for tight spatial
Dynamic spectrum management: Complexity and duality
IEEE Journal of Selected Topics in Signal Processing, vol. 2, no. 1, pp. 57–73, 2008.
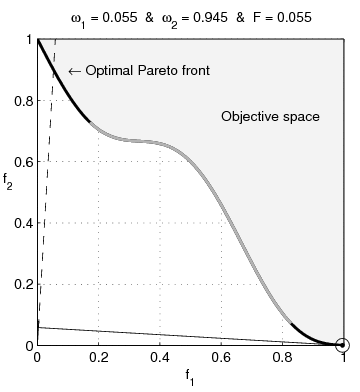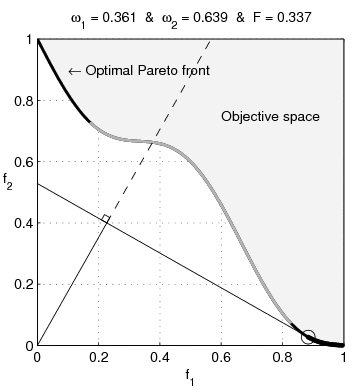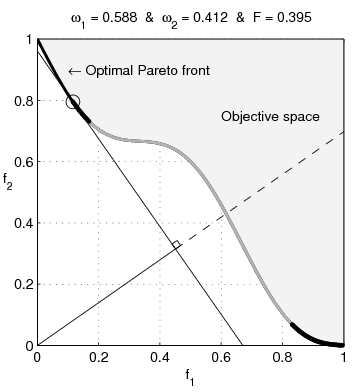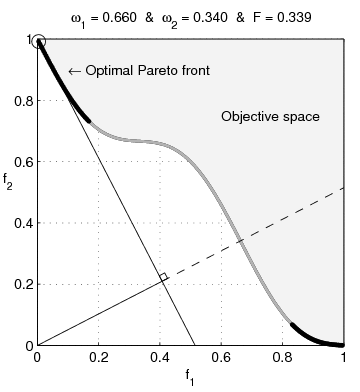 Scalarizing a multi-objective optimization problem is an a priori method, which means formulating a single-objective optimization problem such that optimal solutions to the single-objective optimization problem are Pareto optimal solutions to the multi-objective optimization problem. In addition, it is often required that every Pareto optimal solution can be reached with some parameters of the scalarization. With different parameters for the scalarization, different Pareto optimal solutions are produced. A general formulation for a scalarization of a multi-objective optimization problem is
:
where is a vector parameter, the set is a set depending on the parameter , and is a function.
Very well-known examples are:
* linear scalarization
::
:where the weights of the objectives are the parameters of the scalarization.
* -constraint method (see, e.g.)
::
:where upper bounds are parameters as above and is the objective to be minimized.
Somewhat more advanced examples are the following:
* achievement scalarizing problems of Wierzbicki
:One example of the achievement scalarizing problems can be formulated as
::
:where the term is called the augmentation term, is a small constant, and and are the ''nadir'' and ''utopian'' vectors, respectively. In the above problem, the parameter is the so-called ''reference point'' representing objective function values preferred by the decision maker.
* Sen's multi-objective programming
::
:where is individual optima (absolute) for objectives of maximization and minimization to .
* hypervolume/Chebyshev scalarizationDaniel Golovin and Qiuyi Zhang. Random Hypervolume Scalarizations for Provable Multi-Objective Black Box Optimization. ICML 2021. https://arxiv.org/abs/2006.04655
::
:where the weights of the objectives are the parameters of the scalarization. If the parameters/weights are drawn uniformly in the positive orthant, it is shown that this scalarization provably converges to the Pareto front, even when the front is non-convex.
For example, portfolio optimization is often conducted in terms of mean-variance analysis. In this context, the efficient set is a subset of the portfolios parametrized by the portfolio mean return in the problem of choosing portfolio shares to minimize the portfolio's variance of return subject to a given value of ; see
Scalarizing a multi-objective optimization problem is an a priori method, which means formulating a single-objective optimization problem such that optimal solutions to the single-objective optimization problem are Pareto optimal solutions to the multi-objective optimization problem. In addition, it is often required that every Pareto optimal solution can be reached with some parameters of the scalarization. With different parameters for the scalarization, different Pareto optimal solutions are produced. A general formulation for a scalarization of a multi-objective optimization problem is
:
where is a vector parameter, the set is a set depending on the parameter , and is a function.
Very well-known examples are:
* linear scalarization
::
:where the weights of the objectives are the parameters of the scalarization.
* -constraint method (see, e.g.)
::
:where upper bounds are parameters as above and is the objective to be minimized.
Somewhat more advanced examples are the following:
* achievement scalarizing problems of Wierzbicki
:One example of the achievement scalarizing problems can be formulated as
::
:where the term is called the augmentation term, is a small constant, and and are the ''nadir'' and ''utopian'' vectors, respectively. In the above problem, the parameter is the so-called ''reference point'' representing objective function values preferred by the decision maker.
* Sen's multi-objective programming
::
:where is individual optima (absolute) for objectives of maximization and minimization to .
* hypervolume/Chebyshev scalarizationDaniel Golovin and Qiuyi Zhang. Random Hypervolume Scalarizations for Provable Multi-Objective Black Box Optimization. ICML 2021. https://arxiv.org/abs/2006.04655
::
:where the weights of the objectives are the parameters of the scalarization. If the parameters/weights are drawn uniformly in the positive orthant, it is shown that this scalarization provably converges to the Pareto front, even when the front is non-convex.
For example, portfolio optimization is often conducted in terms of mean-variance analysis. In this context, the efficient set is a subset of the portfolios parametrized by the portfolio mean return in the problem of choosing portfolio shares to minimize the portfolio's variance of return subject to a given value of ; see
General Subpopulation Framework and Taming the Conflict Inside Populations
, Evolutionary computation 23 (1), 1-36. This paradigm searches for novel solutions in objective space (i.e., novelty search on objective space) in addition to the search for non-dominated solutions. Novelty search is like stepping stones guiding the search to previously unexplored places. It is especially useful in overcoming bias and plateaus as well as guiding the search in many-objective optimization problems.
here
. Here, some of the best minds in EMO (Professor Kalyanmoy Deb, Professor Jürgen Branke, etc.) and MCDM (Professor Kaisa Miettinen, Professor Ralph E. Steuer, etc.) realized the potential in combining ideas and approaches of MCDM and EMO fields to prepare hybrids of them. Subsequently, many more Dagstuhl seminars have been arranged to foster collaboration. Recently, hybrid multi-objective optimization has become an important theme in several international conferences in the area of EMO and MCDM (see e.g.,).
International Society on Multiple Criteria Decision Making
Evolutionary Multiobjective Optimization
A Tutorial on Multiobjective Optimization and Genetic Algorithms
Tomoiagă, Bogdan; Chindriş, Mircea; Sumper, Andreas; Sudria-Andreu, Antoni; Villafafila-Robles, Roberto. 2013. "Pareto Optimal Reconfiguration of Power Distribution Systems Using a Genetic Algorithm Based on NSGA-II." Energies 6, no. 3: 1439-1455.
{{Major subfields of optimization Decision analysis Mathematical optimization Multiple-criteria decision analysis
objective function
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost ...
to be optimized simultaneously. Multi-objective is a type of vector optimization
Vector optimization is a subarea of mathematical optimization where Optimization problem, optimization problems with a vector-valued objective functions are optimized with respect to a given partial ordering and subject to certain constraints. A m ...
that has been applied in many fields of science, including engineering, economics and logistics where optimal decisions need to be taken in the presence of trade-offs between two or more conflicting objectives. Minimizing cost while maximizing comfort while buying a car, and maximizing performance whilst minimizing fuel consumption and emission of pollutants of a vehicle are examples of multi-objective optimization problems involving two and three objectives, respectively. In practical problems, there can be more than three objectives.
For a multi-objective optimization problem, it is not guaranteed that a single solution simultaneously optimizes each objective. The objective functions are said to be conflicting. A solution is called nondominated, Pareto optimal, Pareto efficient or noninferior, if none of the objective functions can be improved in value without degrading some of the other objective values. Without additional subjective preference information, there may exist a (possibly infinite) number of Pareto optimal solutions, all of which are considered equally good. Researchers study multi-objective optimization problems from different viewpoints and, thus, there exist different solution philosophies and goals when setting and solving them. The goal may be to find a representative set of Pareto optimal solutions, and/or quantify the trade-offs in satisfying the different objectives, and/or finding a single solution that satisfies the subjective preferences of a human decision maker (DM).
Bicriteria optimization denotes the special case in which there are two objective functions.
There is a direct relationship between multitask optimization and multi-objective optimization.
Introduction
A multi-objective optimization problem is anoptimization problem
In mathematics, engineering, computer science and economics
Economics () is a behavioral science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goo ...
that involves multiple objective functions. In mathematical terms, a multi-objective optimization problem can be formulated as
:
where the integer is the number of objectives and the set is the feasible set of decision vectors, which is typically but it depends on the -dimensional application domain. The feasible set is typically defined by some constraint functions. In addition, the vector-valued objective function is often defined as
:
nadir
The nadir is the direction pointing directly ''below'' a particular location; that is, it is one of two vertical directions at a specified location, orthogonal to a horizontal flat surface.
The direction opposite of the nadir is the zenith.
Et ...
objective vector and an ideal objective vector , if these are finite. The nadir objective vector is defined as
:
and the ideal objective vector as
:
In other words, the components of the nadir and ideal objective vectors define the upper and lower bounds of the objective function of Pareto optimal solutions. In practice, the nadir objective vector can only be approximated as, typically, the whole Pareto optimal set is unknown. In addition, a utopian objective vector , such that where is a small constant, is often defined because of numerical reasons.
Examples of applications
Economics
Ineconomics
Economics () is a behavioral science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services.
Economics focuses on the behaviour and interac ...
, many problems involve multiple objectives along with constraints on what combinations of those objectives are attainable. For example, consumer's demand
In economics, demand is the quantity of a goods, good that consumers are willing and able to purchase at various prices during a given time. In economics "demand" for a commodity is not the same thing as "desire" for it. It refers to both the desi ...
for various goods is determined by the process of maximization of the utilities
A public utility company (usually just utility) is an organization that maintains the infrastructure for a public service (often also providing a service using that infrastructure). Public utilities are subject to forms of public control and r ...
derived from those goods, subject to a constraint based on how much income is available to spend on those goods and on the prices of those goods. This constraint allows more of one good to be purchased only at the sacrifice of consuming less of another good; therefore, the various objectives (more consumption of each good is preferred) are in conflict with each other. A common method for analyzing such a problem is to use a graph of indifference curve
In economics, an indifference curve connects points on a graph representing different quantities of two goods, points between which a consumer is ''indifferent''. That is, any combinations of two products indicated by the curve will provide the c ...
s, representing preferences, and a budget constraint, representing the trade-offs that the consumer is faced with.
Another example involves the production possibilities frontier, which specifies what combinations of various types of goods can be produced by a society with certain amounts of various resources. The frontier specifies the trade-offs that the society is faced with — if the society is fully utilizing its resources, more of one good can be produced only at the expense of producing less of another good. A society must then use some process to choose among the possibilities on the frontier.
Macroeconomic policy
Macroeconomics is a branch of economics that deals with the performance, structure, behavior, and decision-making of an economy as a whole. This includes regional, national, and global economies. Macroeconomists study topics such as output/ GDP ...
-making is a context requiring multi-objective optimization. Typically a central bank
A central bank, reserve bank, national bank, or monetary authority is an institution that manages the monetary policy of a country or monetary union. In contrast to a commercial bank, a central bank possesses a monopoly on increasing the mo ...
must choose a stance for monetary policy
Monetary policy is the policy adopted by the monetary authority of a nation to affect monetary and other financial conditions to accomplish broader objectives like high employment and price stability (normally interpreted as a low and stable rat ...
that balances competing objectives — low inflation
In economics, inflation is an increase in the average price of goods and services in terms of money. This increase is measured using a price index, typically a consumer price index (CPI). When the general price level rises, each unit of curre ...
, low unemployment
Unemployment, according to the OECD (Organisation for Economic Co-operation and Development), is the proportion of people above a specified age (usually 15) not being in paid employment or self-employment but currently available for work du ...
, low balance of trade
Balance of trade is the difference between the monetary value of a nation's exports and imports of goods over a certain time period. Sometimes, trade in Service (economics), services is also included in the balance of trade but the official IMF d ...
deficit, etc. To do this, the central bank uses a model of the economy that quantitatively describes the various causal linkages in the economy; it simulates the model repeatedly under various possible stances of monetary policy, in order to obtain a menu of possible predicted outcomes for the various variables of interest. Then in principle it can use an aggregate objective function to rate the alternative sets of predicted outcomes, although in practice central banks use a non-quantitative, judgement-based, process for ranking the alternatives and making the policy choice.
Finance
Infinance
Finance refers to monetary resources and to the study and Academic discipline, discipline of money, currency, assets and Liability (financial accounting), liabilities. As a subject of study, is a field of Business administration, Business Admin ...
, a common problem is to choose a portfolio when there are two conflicting objectives — the desire to have the expected value
In probability theory, the expected value (also called expectation, expectancy, expectation operator, mathematical expectation, mean, expectation value, or first Moment (mathematics), moment) is a generalization of the weighted average. Informa ...
of portfolio returns be as high as possible, and the desire to have risk
In simple terms, risk is the possibility of something bad happening. Risk involves uncertainty about the effects/implications of an activity with respect to something that humans value (such as health, well-being, wealth, property or the environ ...
, often measured by the standard deviation
In statistics, the standard deviation is a measure of the amount of variation of the values of a variable about its Expected value, mean. A low standard Deviation (statistics), deviation indicates that the values tend to be close to the mean ( ...
of portfolio returns, be as low as possible. This problem is often represented by a graph in which the efficient frontier
In modern portfolio theory, the efficient frontier (or portfolio frontier) is an investment portfolio which occupies the "efficient" parts of the risk–return spectrum.
Formally, it is the set of portfolios which satisfy the condition that n ...
shows the best combinations of risk and expected return that are available, and in which indifference curves show the investor's preferences for various risk-expected return combinations. The problem of optimizing a function of the expected value (first moment) and the standard deviation (square root of the second central moment) of portfolio return is called a two-moment decision model.
Optimal control
Inengineering
Engineering is the practice of using natural science, mathematics, and the engineering design process to Problem solving#Engineering, solve problems within technology, increase efficiency and productivity, and improve Systems engineering, s ...
and economics
Economics () is a behavioral science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services.
Economics focuses on the behaviour and interac ...
, many problems involve multiple objectives which are not describable as the-more-the-better or the-less-the-better; instead, there is an ideal target value for each objective, and the desire is to get as close as possible to the desired value of each objective. For example, energy systems typically have a trade-off between performance and cost or one might want to adjust a rocket's fuel usage and orientation so that it arrives both at a specified place and at a specified time; or one might want to conduct open market operations
In macroeconomics, an open market operation (OMO) is an activity by a central bank to exchange liquidity in its currency with a bank or a group of banks. The central bank can either transact government bonds and other financial assets in the open ...
so that both the inflation rate
In economics, inflation is an increase in the average price of goods and services in terms of money. This increase is measured using a price index, typically a consumer price index (CPI). When the general price level rises, each unit of curre ...
and the unemployment rate
Unemployment, according to the OECD (Organisation for Economic Co-operation and Development), is the proportion of people above a specified age (usually 15) not being in paid employment or self-employment but currently available for work d ...
are as close as possible to their desired values.
Often such problems are subject to linear equality constraints that prevent all objectives from being simultaneously perfectly met, especially when the number of controllable variables is less than the number of objectives and when the presence of random shocks generates uncertainty. Commonly a multi-objective quadratic objective function is used, with the cost associated with an objective rising quadratically with the distance of the objective from its ideal value. Since these problems typically involve adjusting the controlled variables at various points in time and/or evaluating the objectives at various points in time, intertemporal optimization techniques are employed.
Optimal design
Product and process design can be largely improved using modern modeling, simulation, and optimization techniques. The key question in optimal design is measuring what is good or desirable about a design. Before looking for optimal designs, it is important to identify characteristics that contribute the most to the overall value of the design. A good design typically involves multiple criteria/objectives such as capital cost/investment, operating cost, profit, quality and/or product recovery, efficiency, process safety, operation time, etc. Therefore, in practical applications, the performance of process and product design is often measured with respect to multiple objectives. These objectives are typically conflicting, i.e., achieving the optimal value for one objective requires some compromise on one or more objectives. For example, when designing a paper mill, one can seek to decrease the amount of capital invested in a paper mill and enhance the quality of paper simultaneously. If the design of a paper mill is defined by large storage volumes and paper quality is defined by quality parameters, then the problem of optimal design of a paper mill can include objectives such as i) minimization of expected variation of those quality parameters from their nominal values, ii) minimization of the expected time of breaks and iii) minimization of the investment cost of storage volumes. Here, the maximum volume of towers is a design variable. This example of optimal design of a paper mill is a simplification of the model used in. Multi-objective design optimization has also been implemented in engineering systems in the circumstances such as control cabinet layout optimization, airfoil shape optimization using scientific workflows, design of nano-CMOS
Complementary metal–oxide–semiconductor (CMOS, pronounced "sea-moss
", , ) is a type of MOSFET, metal–oxide–semiconductor field-effect transistor (MOSFET) semiconductor device fabrication, fabrication process that uses complementary an ...
, system on chip design, design of solar-powered irrigation systems, optimization of sand mould systems, engine design, optimal sensor deployment and optimal controller design.
Process optimization
Multi-objective optimization has been increasingly employed inchemical engineering
Chemical engineering is an engineering field which deals with the study of the operation and design of chemical plants as well as methods of improving production. Chemical engineers develop economical commercial processes to convert raw materials ...
and manufacturing
Manufacturing is the creation or production of goods with the help of equipment, labor, machines, tools, and chemical or biological processing or formulation. It is the essence of the
secondary sector of the economy. The term may refer ...
. In 2009, Fiandaca and Fraga used the multi-objective genetic algorithm (MOGA) to optimize the pressure swing adsorption process (cyclic separation process). The design problem involved the dual maximization of nitrogen recovery and nitrogen purity. The results approximated the Pareto frontier well with acceptable trade-offs between the objectives.
In 2010, Sendín et al. solved a multi-objective problem for the thermal processing of food. They tackled two case studies (bi-objective and triple-objective problems) with nonlinear dynamic models. They used a hybrid approach consisting of the weighted Tchebycheff and the Normal Boundary Intersection approach. The novel hybrid approach was able to construct a Pareto optimal set for the thermal processing of foods.
In 2013, Ganesan et al. carried out the multi-objective optimization of the combined carbon dioxide reforming and partial oxidation of methane. The objective functions were methane conversion, carbon monoxide selectivity, and hydrogen to carbon monoxide ratio. Ganesan used the Normal Boundary Intersection (NBI) method in conjunction with two swarm-based techniques (Gravitational Search Algorithm (GSA) and Particle Swarm Optimization (PSO)) to tackle the problem. Applications involving chemical extraction and bioethanol production processes have posed similar multi-objective problems.
In 2013, Abakarov et al. proposed an alternative technique to solve multi-objective optimization problems arising in food engineering. The Aggregating Functions Approach, the Adaptive Random Search Algorithm, and the Penalty Functions Approach were used to compute the initial set of the non-dominated or Pareto-optimal solutions. The Analytic Hierarchy Process
In the theory of decision making, the analytic hierarchy process (AHP), also analytical hierarchy process, is a structured technique for organizing and analyzing MCDA, complex decisions, based on mathematics and psychology. It was developed by ...
and Tabular Method were used simultaneously for choosing the best alternative among the computed subset of non-dominated solutions for osmotic dehydration processes.
In 2018, Pearce et al. formulated task allocation to human and robotic workers as a multi-objective optimization problem, considering production time and the ergonomic impact on the human worker as the two objectives considered in the formulation. Their approach used a Mixed-Integer Linear Program to solve the optimization problem for a weighted sum of the two objectives to calculate a set of Pareto optimal solutions. Applying the approach to several manufacturing tasks showed improvements in at least one objective in most tasks and in both objectives in some of the processes.
Radio resource management
The purpose ofradio resource management Radio resource management (RRM) is the system level management of co-channel interference, radio resources, and other radio transmission characteristics in wireless communication systems, for example cellular networks, wireless local area networks, ...
is to satisfy the data rates that are requested by the users of a cellular network.E. Björnson and E. JorswieckOptimal Resource Allocation in Coordinated Multi-Cell Systems
Foundations and Trends in Communications and Information Theory, vol. 9, no. 2-3, pp. 113-381, 2013. The main resources are time intervals, frequency blocks, and transmit powers. Each user has its own objective function that, for example, can represent some combination of the data rate, latency, and energy efficiency. These objectives are conflicting since the frequency resources are very scarce, thus there is a need for tight spatial
frequency reuse
A cellular network or mobile network is a telecommunications network where the link to and from end nodes is wireless network, wireless and the network is distributed over land areas called ''cells'', each served by at least one fixed-locatio ...
which causes immense inter-user interference if not properly controlled. Multi-user MIMO techniques are nowadays used to reduce the interference by adaptive precoding. The network operator would like to both bring great coverage and high data rates, thus the operator would like to find a Pareto optimal solution that balance the total network data throughput and the user fairness in an appropriate subjective manner.
Radio resource management is often solved by scalarization; that is, selection of a network utility function that tries to balance throughput and user fairness. The choice of utility function has a large impact on the computational complexity of the resulting single-objective optimization problem. For example, the common utility of weighted sum rate gives an NP-hard
In computational complexity theory, a computational problem ''H'' is called NP-hard if, for every problem ''L'' which can be solved in non-deterministic polynomial-time, there is a polynomial-time reduction from ''L'' to ''H''. That is, assumi ...
problem with a complexity that scales exponentially with the number of users, while the weighted max-min fairness utility results in a quasi-convex optimization problem with only a polynomial scaling with the number of users.Z.-Q. Luo and S. ZhangDynamic spectrum management: Complexity and duality
IEEE Journal of Selected Topics in Signal Processing, vol. 2, no. 1, pp. 57–73, 2008.
Electric power systems
Reconfiguration, by exchanging the functional links between the elements of the system, represents one of the most important measures which can improve the operational performance of a distribution system. The problem of optimization through the reconfiguration of a power distribution system, in terms of its definition, is a historical single objective problem with constraints. Since 1975, when Merlin and Back introduced the idea of distribution system reconfiguration for active power loss reduction, until nowadays, a lot of researchers have proposed diverse methods and algorithms to solve the reconfiguration problem as a single objective problem. Some authors have proposed Pareto optimality based approaches (including active power losses and reliability indices as objectives). For this purpose, different artificial intelligence based methods have been used: microgenetic, branch exchange, particle swarm optimization and non-dominated sorting genetic algorithm.Inspection of infrastructure
Autonomous inspection of infrastructure has the potential to reduce costs, risks and environmental impacts, as well as ensuring better periodic maintenance of inspected assets. Typically, planning such missions has been viewed as a single-objective optimization problem, where one aims to minimize the energy or time spent in inspecting an entire target structure. For complex, real-world structures, however, covering 100% of an inspection target is not feasible, and generating an inspection plan may be better viewed as a multiobjective optimization problem, where one aims to both maximize inspection coverage and minimize time and costs. A recent study has indicated that multiobjective inspection planning indeed has the potential to outperform traditional methods on complex structuresSolution
As multiple Pareto optimal solutions for multi-objective optimization problems usually exist, what it means to solve such a problem is not as straightforward as it is for a conventional single-objective optimization problem. Therefore, different researchers have defined the term "solving a multi-objective optimization problem" in various ways. This section summarizes some of them and the contexts in which they are used. Many methods convert the original problem with multiple objectives into a single-objectiveoptimization problem
In mathematics, engineering, computer science and economics
Economics () is a behavioral science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goo ...
. This is called a scalarized problem. If the Pareto optimality of the single-objective solutions obtained can be guaranteed, the scalarization is characterized as done neatly.
Solving a multi-objective optimization problem is sometimes understood as approximating or computing all or a representative set of Pareto optimal solutions.
When decision making
In psychology, decision-making (also spelled decision making and decisionmaking) is regarded as the cognitive process resulting in the selection of a belief or a course of action among several possible alternative options. It could be either ra ...
is emphasized, the objective of solving a multi-objective optimization problem is referred to as supporting a decision maker in finding the most preferred Pareto optimal solution according to their subjective preferences. The underlying assumption is that one solution to the problem must be identified to be implemented in practice. Here, a human decision maker
In psychology, decision-making (also spelled decision making and decisionmaking) is regarded as the cognitive process resulting in the selection of a belief or a course of action among several possible alternative options. It could be either ra ...
(DM) plays an important role. The DM is expected to be an expert in the problem domain.
The most preferred results can be found using different philosophies. Multi-objective optimization methods can be divided into four classes.
# In so-called no-preference methods, no DM is expected to be available, but a neutral compromise solution is identified without preference information. The other classes are so-called a priori, a posteriori, and interactive methods, and they all involve preference information from the DM in different ways.
# In a priori methods, preference information is first asked from the DM, and then a solution best satisfying these preferences is found.
# In a posteriori methods, a representative set of Pareto optimal solutions is first found, and then the DM must choose one of them.
# In interactive methods, the decision maker is allowed to search for the most preferred solution iteratively. In each iteration of the interactive method, the DM is shown Pareto optimal solution(s) and describes how the solution(s) could be improved. The information given by the DM is then taken into account while generating new Pareto optimal solution(s) for the DM to study in the next iteration. In this way, the DM learns about the feasibility of their wishes and can concentrate on solutions that are interesting to them. The DM may stop the search whenever they want to.
More information and examples of different methods in the four classes are given in the following sections.
No-preference methods
When a decision maker does not explicitly articulate any preference information, the multi-objective optimization method can be classified as a no-preference method. A well-known example is the method of global criterion, in which a scalarized problem of the form : is solved. In the above problem, can be any norm, with common choices including , , and . The method of global criterion is sensitive to the scaling of the objective functions. Thus, it is recommended that the objectives be normalized into a uniform, dimensionless scale.A priori methods
A priori methods require that sufficient preference information is expressed before the solution process. Well-known examples of a priori methods include the utility function method,lexicographic
Lexicography is the study of lexicons and the art of compiling dictionaries. It is divided into two separate academic disciplines:
* Practical lexicography is the art or craft of compiling, writing and editing dictionaries.
* Theoretical lex ...
method, and goal programming
Goal programming is a branch of multiobjective optimization, which in turn is a branch of multi-criteria decision analysis (MCDA). It can be thought of as an extension or generalisation of linear programming to handle multiple, normally conflicti ...
.
Utility function method
The utility function method assumes the decision maker'sutility function
In economics, utility is a measure of a certain person's satisfaction from a certain state of the world. Over time, the term has been used with at least two meanings.
* In a Normative economics, normative context, utility refers to a goal or ob ...
is available. A mapping is a utility function if for all it holds that if the decision maker prefers to , and if the decision maker is indifferent between and . The utility function specifies an ordering of the decision vectors (recall that vectors can be ordered in many different ways). Once is obtained, it suffices to solve
:
but in practice, it is very difficult to construct a utility function that would accurately represent the decision maker's preferences, particularly since the Pareto front is unknown before the optimization begins.
Lexicographic method
The lexicographic method assumes that the objectives can be ranked in the order of importance. We assume that the objective functions are in the order of importance so that is the most important and the least important to the decision maker. Subject to this assumption, various methods can be used to attain the lexicographically optimal solution. Note that a goal or target value is not specified for any objective here, which makes it different from the LexicographicGoal Programming
Goal programming is a branch of multiobjective optimization, which in turn is a branch of multi-criteria decision analysis (MCDA). It can be thought of as an extension or generalisation of linear programming to handle multiple, normally conflicti ...
method.
Scalarizing
 Scalarizing a multi-objective optimization problem is an a priori method, which means formulating a single-objective optimization problem such that optimal solutions to the single-objective optimization problem are Pareto optimal solutions to the multi-objective optimization problem. In addition, it is often required that every Pareto optimal solution can be reached with some parameters of the scalarization. With different parameters for the scalarization, different Pareto optimal solutions are produced. A general formulation for a scalarization of a multi-objective optimization problem is
:
where is a vector parameter, the set is a set depending on the parameter , and is a function.
Very well-known examples are:
* linear scalarization
::
:where the weights of the objectives are the parameters of the scalarization.
* -constraint method (see, e.g.)
::
:where upper bounds are parameters as above and is the objective to be minimized.
Somewhat more advanced examples are the following:
* achievement scalarizing problems of Wierzbicki
:One example of the achievement scalarizing problems can be formulated as
::
:where the term is called the augmentation term, is a small constant, and and are the ''nadir'' and ''utopian'' vectors, respectively. In the above problem, the parameter is the so-called ''reference point'' representing objective function values preferred by the decision maker.
* Sen's multi-objective programming
::
:where is individual optima (absolute) for objectives of maximization and minimization to .
* hypervolume/Chebyshev scalarizationDaniel Golovin and Qiuyi Zhang. Random Hypervolume Scalarizations for Provable Multi-Objective Black Box Optimization. ICML 2021. https://arxiv.org/abs/2006.04655
::
:where the weights of the objectives are the parameters of the scalarization. If the parameters/weights are drawn uniformly in the positive orthant, it is shown that this scalarization provably converges to the Pareto front, even when the front is non-convex.
For example, portfolio optimization is often conducted in terms of mean-variance analysis. In this context, the efficient set is a subset of the portfolios parametrized by the portfolio mean return in the problem of choosing portfolio shares to minimize the portfolio's variance of return subject to a given value of ; see
Scalarizing a multi-objective optimization problem is an a priori method, which means formulating a single-objective optimization problem such that optimal solutions to the single-objective optimization problem are Pareto optimal solutions to the multi-objective optimization problem. In addition, it is often required that every Pareto optimal solution can be reached with some parameters of the scalarization. With different parameters for the scalarization, different Pareto optimal solutions are produced. A general formulation for a scalarization of a multi-objective optimization problem is
:
where is a vector parameter, the set is a set depending on the parameter , and is a function.
Very well-known examples are:
* linear scalarization
::
:where the weights of the objectives are the parameters of the scalarization.
* -constraint method (see, e.g.)
::
:where upper bounds are parameters as above and is the objective to be minimized.
Somewhat more advanced examples are the following:
* achievement scalarizing problems of Wierzbicki
:One example of the achievement scalarizing problems can be formulated as
::
:where the term is called the augmentation term, is a small constant, and and are the ''nadir'' and ''utopian'' vectors, respectively. In the above problem, the parameter is the so-called ''reference point'' representing objective function values preferred by the decision maker.
* Sen's multi-objective programming
::
:where is individual optima (absolute) for objectives of maximization and minimization to .
* hypervolume/Chebyshev scalarizationDaniel Golovin and Qiuyi Zhang. Random Hypervolume Scalarizations for Provable Multi-Objective Black Box Optimization. ICML 2021. https://arxiv.org/abs/2006.04655
::
:where the weights of the objectives are the parameters of the scalarization. If the parameters/weights are drawn uniformly in the positive orthant, it is shown that this scalarization provably converges to the Pareto front, even when the front is non-convex.
For example, portfolio optimization is often conducted in terms of mean-variance analysis. In this context, the efficient set is a subset of the portfolios parametrized by the portfolio mean return in the problem of choosing portfolio shares to minimize the portfolio's variance of return subject to a given value of ; see Mutual fund separation theorem In Modern portfolio theory, portfolio theory, a mutual fund separation theorem, mutual fund theorem, or separation theorem is a theorem stating that, under certain conditions, any investor's optimal portfolio can be constructed by holding each of ce ...
for details. Alternatively, the efficient set can be specified by choosing the portfolio shares to maximize the function ; the set of efficient portfolios consists of the solutions as ranges from zero to infinity.
Some of the above scalarizations involve invoking the minimax
Minimax (sometimes Minmax, MM or saddle point) is a decision rule used in artificial intelligence, decision theory, combinatorial game theory, statistics, and philosophy for ''minimizing'' the possible loss function, loss for a Worst-case scenari ...
principle, where always the worst of the different objectives is optimized.
A posteriori methods
A posteriori methods aim at producing all the Pareto optimal solutions or a representative subset of the Pareto optimal solutions. Most a posteriori methods fall into either one of the following three classes: *Mathematical programming
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfiel ...
-based a posteriori methods where an algorithm is run repeatedly, each run producing one Pareto optimal solution;
* Evolutionary algorithm
Evolutionary algorithms (EA) reproduce essential elements of the biological evolution in a computer algorithm in order to solve "difficult" problems, at least Approximation, approximately, for which no exact or satisfactory solution methods are k ...
s where one run of the algorithm produces a set of Pareto optimal solutions;
* Deep learning
Deep learning is a subset of machine learning that focuses on utilizing multilayered neural networks to perform tasks such as classification, regression, and representation learning. The field takes inspiration from biological neuroscience a ...
methods where a model is first trained on a subset of solutions and then queried to provide other solutions on the Pareto front.
Mathematical programming
Well-known examples of mathematical programming-based a posteriori methods are the Normal Boundary Intersection (NBI), Modified Normal Boundary Intersection (NBIm), Normal Constraint (NC), Successive Pareto Optimization (SPO), and Directed Search Domain (DSD) methods, which solve the multi-objective optimization problem by constructing several scalarizations. The solution to each scalarization yields a Pareto optimal solution, whether locally or globally. The scalarizations of the NBI, NBIm, NC, and DSD methods are constructed to obtain evenly distributed Pareto points that give a good approximation of the real set of Pareto points.Evolutionary algorithms
Evolutionary algorithms
Evolutionary algorithms (EA) reproduce essential elements of the biological evolution in a computer algorithm in order to solve "difficult" problems, at least Approximation, approximately, for which no exact or satisfactory solution methods are k ...
are popular approaches to generating Pareto optimal solutions to a multi-objective optimization problem. Most evolutionary multi-objective optimization (EMO) algorithms apply Pareto-based ranking schemes. Evolutionary algorithms such as the Non-dominated Sorting Genetic Algorithm-II (NSGA-II), its extended version NSGA-III, Strength Pareto Evolutionary Algorithm 2 (SPEA-2) and multiobjective differential evolution variants have become standard approaches, although some schemes based on particle swarm optimization and simulated annealing
Simulated annealing (SA) is a probabilistic technique for approximating the global optimum of a given function. Specifically, it is a metaheuristic to approximate global optimization in a large search space for an optimization problem. ...
are significant. The main advantage of evolutionary algorithms, when applied to solve multi-objective optimization problems, is the fact that they typically generate sets of solutions, allowing computation of an approximation of the entire Pareto front. The main disadvantage of evolutionary algorithms is their lower speed and the Pareto optimality of the solutions cannot be guaranteed; it is only known that none of the generated solutions is dominated by another.
Another paradigm for multi-objective optimization based on novelty using evolutionary algorithms was recently improved upon.Danilo Vasconcellos Vargas, Junichi Murata, Hirotaka Takano, Alexandre Claudio Botazzo Delbem (2015),General Subpopulation Framework and Taming the Conflict Inside Populations
, Evolutionary computation 23 (1), 1-36. This paradigm searches for novel solutions in objective space (i.e., novelty search on objective space) in addition to the search for non-dominated solutions. Novelty search is like stepping stones guiding the search to previously unexplored places. It is especially useful in overcoming bias and plateaus as well as guiding the search in many-objective optimization problems.
Deep learning methods
Deep learning
Deep learning is a subset of machine learning that focuses on utilizing multilayered neural networks to perform tasks such as classification, regression, and representation learning. The field takes inspiration from biological neuroscience a ...
conditional methods are new approaches to generating several Pareto optimal solutions. The idea is to use the generalization capacity of deep neural networks to learn a model of the entire Pareto front from a limited number of example trade-offs along that front, a task called ''Pareto Front Learning''. Several approaches address this setup, including using hypernetworks and using Stein variational gradient descent.
List of methods
Commonly known a posteriori methods are listed below: * ε-constraint method * Pareto-Hypernetworks * Multi-objective Branch-and-Bound * Normal Boundary Intersection (NBI) * Modified Normal Boundary Intersection (NBIm) * Normal Constraint (NC) * Successive Pareto Optimization (SPO) * Directed Search Domain (DSD) * NSGA-II * PGEN (Pareto surface generation for convex multi-objective instances) * IOSO (Indirect Optimization on the basis of Self-Organization) * SMS-EMOA (S-metric selection evolutionary multi-objective algorithm) * Approximation-Guided Evolution (first algorithm to directly implement and optimize the formal concept ofapproximation
An approximation is anything that is intentionally similar but not exactly equal to something else.
Etymology and usage
The word ''approximation'' is derived from Latin ''approximatus'', from ''proximus'' meaning ''very near'' and the prefix ...
from theoretical computer science)
* Reactive Search Optimization (using machine learning for adapting strategies and objectives), implemented in LIONsolver
* Benson's algorithm for multi-objective linear programs and for multi-objective convex programs
* Multi-objective particle swarm optimization
* Subpopulation Algorithm based on Novelty
* MOEA/D (Multi-Objective Evolutionary Algorithm based on Decomposition)
Interactive methods
In interactive methods of optimizing multiple objective problems, the solution process is iterative and the decision maker continuously interacts with the method when searching for the most preferred solution (see e.g., Miettinen 1999, Miettinen 2008). In other words, the decision maker is expected to express preferences at each iteration to get ''Pareto optimal solutions'' that are of interest to the decision maker and learn what kind of solutions are attainable. The following steps are commonly present in interactive methods of optimization: # initialize (e.g., calculate ideal and approximated nadir objective vectors and show them to the decision maker) # generate a Pareto optimal starting point (by using e.g., some no-preference method or solution given by the decision maker) # ask for preference information from the decision maker (e.g., aspiration levels or number of new solutions to be generated) # generate new Pareto optimal solution(s) according to the preferences and show it/them and possibly some other information about the problem to the decision maker # if several solutions were generated, ask the decision maker to select the best solution so far # stop (if the decision maker wants to; otherwise, go to step 3). The above aspiration levels refer to desirable objective function values forming a reference point. Instead of mathematical convergence, often used as a stopping criterion inmathematical optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfiel ...
methods, psychological convergence is often emphasized in interactive methods. Generally speaking, a method is terminated when the decision maker is confident that he/she has found the ''most preferred solution available''.
Types of preference information
There are different interactive methods involving different types of preference information. Three types can be identified based on # trade-off information, # reference points, and # classification of objective functions. On the other hand, a fourth type of generating a small sample of solutions is included in: An example of the interactive method utilizing trade-off information is the Zionts-Wallenius method, where the decision maker is shown several objective trade-offs at each iteration, and (s)he is expected to say whether (s)he likes, dislikes, or is indifferent with respect to each trade-off. In reference point-based methods (see e.g.,), the decision maker is expected at each iteration to specify a reference point consisting of desired values for each objective and a corresponding Pareto optimal solution(s) is then computed and shown to them for analysis. In classification-based interactive methods, the decision maker is assumed to give preferences in the form of classifying objectives at the current Pareto optimal solution into different classes, indicating how the values of the objectives should be changed to get a more preferred solution. Then, the classification information is considered when new (more preferred) Pareto optimal solution(s) are computed. In the satisficing trade-off method (STOM), three classes are used: objectives whose values 1) should be improved, 2) can be relaxed, and 3) are acceptable as such. In the NIMBUS method, two additional classes are also used: objectives whose values 4) should be improved until a given bound and 5) can be relaxed until a given bound.Hybrid methods
Different hybrid methods exist, but here we consider hybridizing MCDM ( multi-criteria decision-making) and EMO (evolutionary multi-objective optimization). A hybrid algorithm in multi-objective optimization combines algorithms/approaches from these two fields (see e.g.,). Hybrid algorithms of EMO and MCDM are mainly used to overcome shortcomings by utilizing strengths. Several types of hybrid algorithms have been proposed in the literature, e.g., incorporating MCDM approaches into EMO algorithms as a local search operator, leading a DM to the most preferred solution(s), etc. A local search operator is mainly used to enhance the rate of convergence of EMO algorithms. The roots for hybrid multi-objective optimization can be traced to the first Dagstuhl seminar organized in November 2004 (sehere
. Here, some of the best minds in EMO (Professor Kalyanmoy Deb, Professor Jürgen Branke, etc.) and MCDM (Professor Kaisa Miettinen, Professor Ralph E. Steuer, etc.) realized the potential in combining ideas and approaches of MCDM and EMO fields to prepare hybrids of them. Subsequently, many more Dagstuhl seminars have been arranged to foster collaboration. Recently, hybrid multi-objective optimization has become an important theme in several international conferences in the area of EMO and MCDM (see e.g.,).
Visualization of the Pareto front
Visualization of the Pareto front is one of the a posteriori preference techniques of multi-objective optimization. The a posteriori preference techniques provide an important class of multi-objective optimization techniques. Usually, the a posteriori preference techniques include four steps: (1) computer approximates the Pareto front, i.e., the Pareto optimal set in the objective space; (2) the decision maker studies the Pareto front approximation; (3) the decision maker identifies the preferred point at the Pareto front; (4) computer provides the Pareto optimal decision, whose output coincides with the objective point identified by the decision maker. From the point of view of the decision maker, the second step of the a posteriori preference techniques is the most complicated. There are two main approaches to informing the decision maker. First, a number of points of the Pareto front can be provided in the form of a list (interesting discussion and references are given in) or using heatmaps.Visualization in bi-objective problems: tradeoff curve
In the case of bi-objective problems, informing the decision maker concerning the Pareto front is usually carried out by its visualization: the Pareto front, often named the tradeoff curve in this case, can be drawn at the objective plane. The tradeoff curve gives full information on objective values and on objective tradeoffs, which inform how improving one objective is related to deteriorating the second one while moving along the tradeoff curve. The decision maker takes this information into account while specifying the preferred Pareto optimal objective point. The idea to approximate and visualize the Pareto front was introduced for linear bi-objective decision problems by S. Gass and T. Saaty. This idea was developed and applied in environmental problems by J.L. Cohon. A review of methods for approximating the Pareto front for various decision problems with a small number of objectives (mainly, two) is provided in.Visualization in high-order multi-objective optimization problems
There are two generic ideas for visualizing the Pareto front in high-order multi-objective decision problems (problems with more than two objectives). One of them, which is applicable in the case of a relatively small number of objective points that represent the Pareto front, is based on using the visualization techniques developed in statistics (various diagrams, etc.; see the corresponding subsection below). The second idea proposes the display of bi-objective cross-sections (slices) of the Pareto front. It was introduced by W.S. Meisel in 1973 who argued that such slices inform the decision maker on objective tradeoffs. The figures that display a series of bi-objective slices of the Pareto front for three-objective problems are known as the decision maps. They give a clear picture of tradeoffs between the three criteria. The disadvantages of such an approach are related to the following two facts. First, the computational procedures for constructing the Pareto front's bi-objective slices are unstable since the Pareto front is usually not stable. Secondly, it is applicable in the case of only three objectives. In the 1980s, the idea of W.S. Meisel was implemented in a different form—in the form of the Interactive Decision Maps (IDM) technique. More recently, N. Wesner proposed using a combination of a Venn diagram and multiple scatterplots of the objective space to explore the Pareto frontier and select optimal solutions.See also
*Concurrent programming
Concurrent means happening at the same time. Concurrency, concurrent, or concurrence may refer to:
Law
* Concurrence, in jurisprudence, the need to prove both ''actus reus'' and ''mens rea''
* Concurring opinion (also called a "concurrence"), a ...
*Decision-making software
Decision-making software (DM software) is software for computer applications that help individuals and organisations make choices and take decisions, typically by ranking, prioritizing or choosing from a number of options.
An early example of DM s ...
*Goal programming
Goal programming is a branch of multiobjective optimization, which in turn is a branch of multi-criteria decision analysis (MCDA). It can be thought of as an extension or generalisation of linear programming to handle multiple, normally conflicti ...
* Interactive Decision Maps
* Multiple-criteria decision-making
* Multi-objective linear programming
* Multi-disciplinary design optimization
*Pareto efficiency
In welfare economics, a Pareto improvement formalizes the idea of an outcome being "better in every possible way". A change is called a Pareto improvement if it leaves at least one person in society better off without leaving anyone else worse ...
*Utility function
In economics, utility is a measure of a certain person's satisfaction from a certain state of the world. Over time, the term has been used with at least two meanings.
* In a Normative economics, normative context, utility refers to a goal or ob ...
*Vector optimization
Vector optimization is a subarea of mathematical optimization where Optimization problem, optimization problems with a vector-valued objective functions are optimized with respect to a given partial ordering and subject to certain constraints. A m ...
References
External links
* Emmerich, M.T.M., Deutz, A.H. A tutorial on multiobjective optimization: fundamentals and evolutionary methods. Nat Comput 17, 585–609 (2018). https://doi.org/10.1007/s11047-018-9685-yInternational Society on Multiple Criteria Decision Making
Evolutionary Multiobjective Optimization
The Wolfram Demonstrations Project
The Wolfram Demonstrations Project is an open-source collection of interactive programmes called Demonstrations. It is hosted by Wolfram Research. At its launch, it contained 1300 demonstrations but has grown to over 10,000. The site won a Pa ...
A Tutorial on Multiobjective Optimization and Genetic Algorithms
Scilab
Scilab is a free and open-source, cross-platform numerical computational package and a high-level, numerically oriented programming language. It can be used for signal processing, statistical analysis, image enhancement, fluid dynamics simul ...
Professional Partner
Tomoiagă, Bogdan; Chindriş, Mircea; Sumper, Andreas; Sudria-Andreu, Antoni; Villafafila-Robles, Roberto. 2013. "Pareto Optimal Reconfiguration of Power Distribution Systems Using a Genetic Algorithm Based on NSGA-II." Energies 6, no. 3: 1439-1455.
{{Major subfields of optimization Decision analysis Mathematical optimization Multiple-criteria decision analysis