Morse Potential

The Morse potential, named after physicist Philip M. Morse, is a convenient
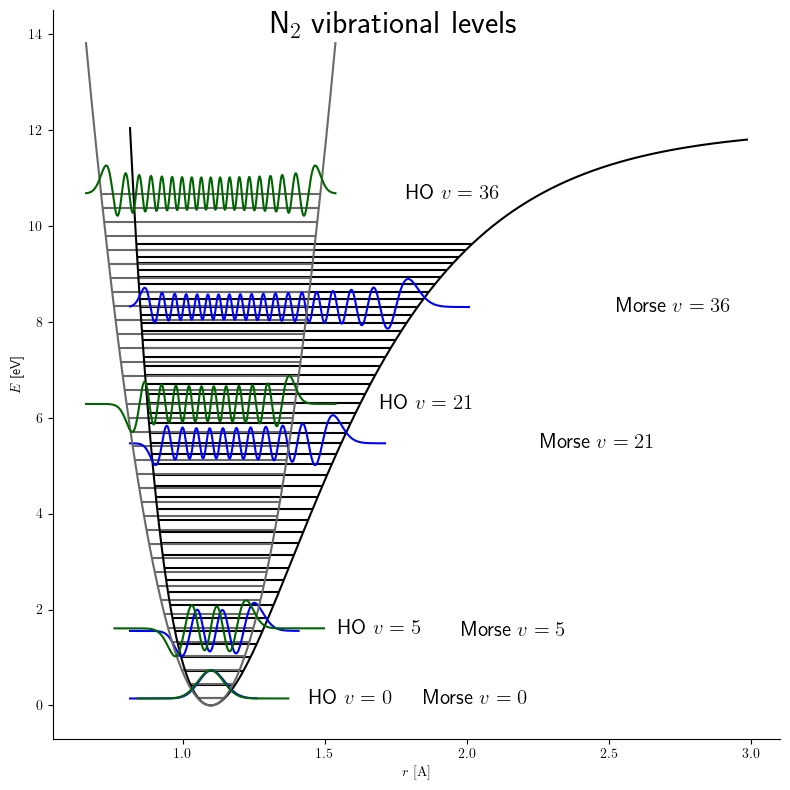
interatomic interaction model for the potential energy of a diatomic molecule. It is a better approximation for the vibrational structure of the molecule than the quantum harmonic oscillator because it explicitly includes the effects of bond breaking, such as the existence of unbound states. It also accounts for the anharmonicity of real bonds and the non-zero transition probability for overtone and combination bands. The Morse potential can also be used to model other interactions such as the interaction between an atom and a surface. Due to its simplicity (only three fitting parameters), it is not used in modern spectroscopy. However, its mathematical form inspired the MLR ( Morse/Long-range) potential, which is the most popular potential energy function used for fitting spectroscopic data.

Potential energy function

The Morse potential energy function is of the form

:$V(r) = D_e ( 1-e^ )^2$

Here $r$ is the distance between the atoms, $r_e$ is the equilibrium bond distance, $D_e$ is the well depth (defined relative to the dissociated atoms), and $a$ controls the 'width' of the potential (the smaller $a$ is, the larger the well). The dissociation energy of the bond can be calculated by subtracting the zero point energy $E_0$ from the depth of the well. The force constant (stiffness) of the bond can be found by Taylor expansion of $V'(r)$ around $r=r_e$ to the second derivative of the potential energy function, from which it can be shown that the parameter, $a$, is

:$a = \sqrt\ ,$

where $k_e$ is the force constant at the minimum of the well.

Since the zero of potential energy is arbitrary, the equation for the Morse potential can be rewritten any number of ways by adding or subtracting a constant value. When it is used to model the atom-surface interaction, the energy zero can be redefined so that the Morse potential becomes

:$V(r)= V'(r)-D_e = D_e ( 1-e^ )^2 -D_e$
which is usually written as

:$V(r) = D_e ( e^-2e^ )$

where $r$ is now the coordinate perpendicular to the surface. This form approaches zero at infinite $r$ and equals $-D_e$ at its minimum, i.e. $r=r_e$. It clearly shows that the Morse potential is the combination of a short-range repulsion term (the former) and a long-range attractive term (the latter), analogous to the Lennard-Jones potential.

Vibrational states and energies

Like the quantum harmonic oscillator, the energies and eigenstates of the Morse potential can be found using operator methods.
One approach involves applying the factorization method to the Hamiltonian.

To write the stationary states on the Morse potential, i.e. solutions $\ \Psi_n(r)\$ and $\ E_n\$ of the following Schrödinger equation:

:$\left(-\frac\frac+V(r)\right)\Psi_n(r)=E_n\Psi_n(r)\ ,$

it is convenient to introduce the new variables:

:$x \equiv a\ r\ \text \quad x_e \equiv a\ r_e\ \text \quad \lambda \equiv \frac\ \text \quad \varepsilon_n \equiv \frac\ E_n = \fracE_n ~.$

Then, the Schrödinger equation takes the simplified form:

:$\left( -\frac + V(x) \right)\ \Psi_n(x) = \varepsilon_n\ \Psi_n(x)\ ,$
:$V(x) = \lambda^2 \left( 1 - e^ \right)^2 ~.$
Its eigenvalues (reduced by $\ D_e\$) and eigenstates can be written as:
:$\varepsilon_n = \lambda^2 - \left(\lambda - n - \tfrac \right)^2 = 2\lambda \left( n +\tfrac \right) - \left( n + \tfrac \right)^2 = \left( 2\lambda - n - \tfrac \right) \left( n + \tfrac \right)\ ,$
where
:$n = 0,\ 1,\ \ldots,\ \lfloor \lambda - \tfrac \rfloor\ ,$
with $\ \lfloor x \rfloor\$ denoting the largest integer smaller than $\ x\ ,$ and
:$\Psi_n(z) = N_n\ z^\ e^\ L_n^(z)\ ,$
where
$~ z \equiv 2\ \lambda\ e^ ~$
and
$~ N_n \equiv \sqrt ~$
which satisfies the normalization condition
:$\int \Psi_n^(r)\ \Psi_n(r)\ \operatornamer = 1$

and where $\ L_n^(z)\$ is a generalized Laguerre polynomial:
:$L_n^(z) ~=~ \frac\ \frac \left( z^ e^ \right) ~=~ \frac \; _1 F_1( -n,\alpha + 1, z ) ~.$

There also exists the following analytical expression for matrix elements of the coordinate operator:
:$\left\langle \Psi_m \bigl, \ x\ \bigr, \Psi_n \right\rangle = \frac\ \sqrt ~.$
which is valid for $~ m > n ~$ and $~ N = \lambda - \tfrac ~.$

The eigenenergies in the initial variables have the form:
:$E_n = h\ \nu_0 \left( n + \tfrac \right) - \frac$

where $\ n\$ is the vibrational quantum number and $\ \nu_0\$ has units of frequency. The latter is mathematically related to the particle mass, $\ m\ ,$ and the Morse constants via

:$\nu_0 = \frac \sqrt ~.$

Whereas the energy spacing between vibrational levels in the quantum harmonic oscillator is constant at $\ h\ \nu_0\ ,$ the energy between adjacent levels decreases with increasing $\ v\$ in the Morse oscillator. Mathematically, the spacing of Morse levels is

:$E_ - E_n = h\ \nu_0 - \frac ~.$

This trend matches the inharmonicity found in real molecules. However, this equation fails above some value of $\ n_m\$ where $\ E(n_m + 1) - E(n_m)\$ is calculated to be zero or negative. Specifically,

:$n_m = \frac\$ (integer part only).

This failure is due to the ''finite'' number of bound levels in the Morse potential, and some maximum $\ n_m\$ that remains bound. For energies above $\ n_m\ ,$ all the possible energy levels are allowed and the equation for $\ E_n\$ is no longer valid.

Below $\ n_m\ ,$ $\ E_n\$ is a good approximation for the true vibrational structure in non-rotating diatomic molecules. In fact, the real molecular spectra are generally fit to the form

:$E_n / hc = \omega_e \left( n + \tfrac \right) - \omega_e\ \chi_e \left( n +\tfrac \right)^2\$

in which the constants $\ \omega_e\$ and $\ \omega_e\ \chi_e\$ can be directly related to the parameters for the Morse potential. Specifically,

:$a = \sqrt$

and

:$D_e = \frac$

Note that if $\ \omega_e\$ and $\ \omega_e\ \chi_e\$ are given in $\ \mathsf^\ ,$ $\ c\$ is in cm/s (not m/s), $\ m\$ is in kg, and $\ h\$ is in in which case $\ a\$ will be in $\ \mathsf^\$ and $\ D_e\$ will be in $\mathsf^ ~.$

As is clear from dimensional analysis, for historical reasons the last equation uses spectroscopic notation in which $\ \omega_e\$ represents a wavenumber obeying $\ E = h\ c\ \omega\ ,$ and not an angular frequency given by $\ E = \hbar\ \omega ~.$

Morse/Long-range potential

An extension of the Morse potential that made the Morse form useful for modern (high-resolution) spectroscopy is the MLR ( Morse/Long-range) potential. The MLR potential is used as a standard for representing spectroscopic and/or virial data of diatomic molecules by a potential energy curve. It has been used on N₂, Ca₂, KLi, MgH, several electronic states of Li₂, Cs₂, Sr₂, ArXe, LiCa, LiNa, Br₂, Mg₂, HF, HCl, HBr, HI, MgD, Be₂, BeH, and NaH. More sophisticated versions are used for polyatomic molecules.

See also

*Lennard-Jones potential
*Molecular mechanics

References

*¹ CRC Handbook of chemistry and physics, Ed David R. Lide, 87th ed, Section 9, ''SPECTROSCOPIC CONSTANTS OF DIATOMIC MOLECULES'' pp. 9–82
*
*
*
*
*
*
*
* Khordad, R; Edet, C.O; and Ikot, A.N. (2022). "Application of Morse potential and improved deformed exponential-type potential (IDEP) model to predict thermodynamics properties of diatomic molecules" ''International Journal of Modern Physics C'' 33 (08): 225010

Digital object identifier, doi:10.1142/S0129183122501066
* Varshni, Yatendra Pal, (1957) "Comparative Study of Potential Energy Functions for Diatomic Molecules" ''Rev. Mod. Phys.'' 29: 664 doi:10.1103/RevModPhys.29.664
* Kaplan, I.G. (2003) ''Handbook of Molecular Physics and Quantum Chemistry'', Wiley, p207.
* Haynes W M, David R and Lide T J B (eds) (2017) ''CRC Handbook of Chemistry and Physics'', Boca Raton, FL: CRC Press

{{DEFAULTSORT:Morse Potential
Chemical bonding
Quantum chemistry
Quantum models
Quantum mechanical potentials