Molar Enthalpy

Enthalpy () is the sum of a thermodynamic system's internal energy and the product of its pressure and volume. It is a state function in thermodynamics used in many measurements in chemical, biological, and physical systems at a constant external pressure, which is conveniently provided by the large ambient atmosphere. The pressure–volume term expresses the work $W$ that was done against constant external pressure $P_\text$ to establish the system's physical dimensions from $V_\text=0$ to some final volume $V_\text$ (as $W=P_\text\Delta V$), i.e. to make room for it by displacing its surroundings.
The pressure-volume term is very small for solids and liquids at common conditions, and fairly small for gases. Therefore, enthalpy is a stand-in for energy in chemical systems; bond, lattice, solvation, and other chemical "energies" are actually enthalpy differences. As a state function, enthalpy depends only on the final configuration of internal energy, pressure, and volume, not on the path taken to achieve it.

In the International System of Units (SI), the unit of measurement for enthalpy is the joule. Other historical conventional units still in use include the calorie and the British thermal unit (BTU).

The total enthalpy of a system cannot be measured directly because the internal energy contains components that are unknown, not easily accessible, or are not of interest for the thermodynamic problem at hand. In practice, a change in enthalpy is the preferred expression for measurements at constant pressure, because it simplifies the description of energy transfer. When transfer of matter into or out of the system is also prevented and no electrical or mechanical (stirring shaft or lift pumping) work is done, at constant pressure the enthalpy change equals the energy exchanged with the environment by heat.

In chemistry, the standard enthalpy of reaction is the enthalpy change when reactants in their standard states ( usually ) change to products in their standard states.
This quantity is the standard heat of reaction at constant pressure and temperature, but it can be measured by calorimetric methods even if the temperature does vary during the measurement, provided that the initial and final pressure and temperature correspond to the standard state. The value does not depend on the path from initial to final state because enthalpy is a state function.

Enthalpies of chemical substances are usually listed for pressure as a standard state. Enthalpies and enthalpy changes for reactions vary as a function of temperature,
but tables generally list the standard heats of formation of substances at . For endothermic (heat-absorbing) processes, the change is a positive value; for exothermic (heat-releasing) processes it is negative.

The enthalpy of an ideal gas is independent of its pressure or volume, and depends only on its temperature, which correlates to its thermal energy. Real gases at common temperatures and pressures often closely approximate this behavior, which simplifies practical thermodynamic design and analysis.

The word "enthalpy" is derived from the Greek word ''enthalpein'', which means "to heat".

Definition

The enthalpy of a thermodynamic system is defined as the sum of its internal energy and the product of its pressure and volume:
$H = U + p V,$
where is the internal energy, is pressure, and is the volume of the system; is sometimes referred to as the pressure energy .

Enthalpy is an extensive property; it is proportional to the size of the system (for homogeneous systems). As intensive properties, the ''specific enthalpy'' is referenced to a unit of mass of the system, and the ''molar enthalpy'' where is the number of moles. For inhomogeneous systems the enthalpy is the sum of the enthalpies of the component subsystems:
$H = \sum_k H_k,$
where
: is the total enthalpy of all the subsystems,
: refers to the various subsystems,
: refers to the enthalpy of each subsystem.

A closed system may lie in thermodynamic equilibrium in a static gravitational field, so that its pressure varies continuously with altitude, while, because of the equilibrium requirement, its temperature is invariant with altitude. (Correspondingly, the system's gravitational potential energy density also varies with altitude.) Then the enthalpy summation becomes an integral:
$H = \int \rho h \,\mathrmV,$
where
: ("rho") is density (mass per unit volume),
: is the specific enthalpy (enthalpy per unit mass),
: represents the enthalpy density (enthalpy per unit volume),
: denotes an infinitesimally small element of volume within the system, for example, the volume of an infinitesimally thin horizontal layer.
The integral therefore represents the sum of the enthalpies of all the elements of the volume.

The enthalpy of a closed homogeneous system is its energy function with its entropy and its pressure as natural state variables which provide a differential relation for of the simplest form, derived as follows. We start from the first law of thermodynamics for closed systems for an infinitesimal process:
$\mathrmU = \delta Q - \delta W,$
where
: is a small amount of heat added to the system,
: is a small amount of work performed by the system.

In a homogeneous system in which only reversible processes or pure heat transfer are considered, the second law of thermodynamics gives with the absolute temperature and the infinitesimal change in entropy of the system. Furthermore, if only work is done, As a result,
$\mathrmU = T\,\mathrmS - p\,\mathrmV.$

Adding to both sides of this expression gives
$\mathrmU + \mathrm(pV) = T\,\mathrmS - p\,\mathrmV + \mathrm(p\,V),$
or
$\mathrm(U + pV) = T\,\mathrmS + V\,\mathrmp.$
So
$\mathrmH(S, p) = T\,\mathrmS + V\,\mathrmp,$
and the coefficients of the natural variable differentials and are just the single variables and .

Other expressions

The above expression of in terms of entropy and pressure may be unfamiliar to some readers. There are also expressions in terms of more directly measurable variables such as temperature and pressure:

$\mathrmH = C_\mathsf\,\mathrmT + V(1 - \alpha T)\,\mathrmp,$
where is the heat capacity at ''constant pressure'', and is the coefficient of (cubic) thermal expansion:
$\alpha = \frac \left(\frac\right)_p.$

With this expression one can, in principle, determine the enthalpy if and are known as functions of and . However the expression is more complicated than $\mathrmH = T\,\mathrmS + V\,\mathrmp$ because is not a natural variable for the enthalpy .

At constant pressure, $\mathrmP = 0$ so that $\mathrmH = C_\mathsf\,\mathrmT.$ For an ideal gas, $\mathrmH$ reduces to this form even if the process involves a pressure change, because $\alpha T = \frac \left(\frac\right)_p = \frac = 1.$

In a more general form, the first law describes the internal energy with additional terms involving the chemical potential and the number of particles of various types. The differential statement for then becomes
$\mathrmH = T\,\mathrmS + V\,\mathrmp + \sum_i \mu_i\,\mathrmN_i,$
where is the chemical potential per particle for a type  particle, and is the number of such particles. The last term can also be written as (with the number of moles of component added to the system and, in this case, the molar chemical potential) or as (with the mass of component added to the system and, in this case, the specific chemical potential).

Characteristic functions and natural state variables

The enthalpy expresses the thermodynamics of a system in the ''energy representation''. As a function of state, its arguments include one intensive and several extensive state variables. The state variables , and are said to be the ''natural state variables'' in this representation. They are suitable for describing processes in which they are determined by factors in the surroundings. For example, when a virtual parcel of atmospheric air moves to a different altitude, the pressure surrounding it changes, and the process is often so rapid that there is too little time for heat transfer. This is the basis of the so-called adiabatic approximation that is used in meteorology.

Conjugate with the enthalpy, with these arguments, the other characteristic function of state of a thermodynamic system is its entropy, as a function of the same list of variables of state, except that the entropy is replaced in the list by the enthalpy . It expresses the ''entropy representation''. The state variables , , and are said to be the ''natural state variables'' in this representation. They are suitable for describing processes in which they are experimentally controlled. For example, and can be controlled by allowing heat transfer, and by varying only the external pressure on the piston that sets the volume of the system.

Physical interpretation

The term is the energy of the system, and the term can be interpreted as the work that would be required to "make room" for the system if the pressure of the environment remained constant. When a system, for example, moles of a gas of volume at pressure and temperature , is created or brought to its present state from absolute zero, energy must be supplied equal to its internal energy plus , where is the work done in pushing against the ambient (atmospheric) pressure.

In physics and statistical mechanics it may be more interesting to study the internal properties of a constant-volume system and therefore the internal energy is used.
In chemistry, experiments are often conducted at constant atmospheric pressure, and the pressure–volume work represents a small, well-defined energy exchange with the atmosphere, so that is the appropriate expression for the heat of reaction. For a heat engine, the change in its enthalpy after a full cycle is equal to zero, since the final and initial state are equal.

Relationship to heat

In order to discuss the relation between the enthalpy increase and heat supply, we return to the first law for closed systems, with the physics sign convention: , where the heat is supplied by conduction, radiation, Joule heating. We apply it to the special case with a constant pressure at the surface. In this case the work is given by (where is the pressure at the surface, is the increase of the volume of the system). Cases of long-range electromagnetic interaction require further state variables in their formulation and are not considered here. In this case the first law reads:
$\mathrmU = \delta Q - p \,\mathrmV.$
Now,
$\mathrmH = \mathrmU + \mathrm(pV),$
so
$\begin \mathrmH &= \delta Q + V \,\mathrmp + p \,\mathrmV - p \,\mathrmV \\ &= \delta Q + V \,\mathrmp. \end$

If the system is under constant pressure, and consequently, the increase in enthalpy of the system is equal to the heat added:
$\mathrmH = \delta Q.$
This is why the now-obsolete term ''heat content'' was used for enthalpy in the 19th century.

Applications

In thermodynamics, one can calculate enthalpy by determining the requirements for creating a system from "nothingness"; the mechanical work required, differs based upon the conditions that obtain during the creation of the thermodynamic system.

Energy must be supplied to remove particles from the surroundings to make space for the creation of the system, assuming that the pressure remains constant; this is the term. The supplied energy must also provide the change in internal energy , which includes activation energies, ionization energies, mixing energies, vaporization energies, chemical bond energies, and so forth. Together, these constitute the change in the enthalpy For systems at constant pressure, with no external work done other than the work, the change in enthalpy is the heat received by the system.

For a simple system with a constant number of particles at constant pressure, the difference in enthalpy is the maximum amount of thermal energy derivable from an isobaric thermodynamic process.

Heat of reaction

The total enthalpy of a system cannot be measured directly; the ''enthalpy change'' of a system is measured instead. Enthalpy change is defined by the following equation:
$\Delta H = H_\text - H_\text,$
where
: is the "enthalpy change",
: is the final enthalpy of the system (in a chemical reaction, the enthalpy of the products or the system at equilibrium),
: is the initial enthalpy of the system (in a chemical reaction, the enthalpy of the reactants).

For an exothermic reaction at constant pressure, the system's change in enthalpy, , is negative due to the products of the reaction having a smaller enthalpy than the reactants, and equals the heat released in the reaction if no electrical or mechanical work is done. In other words, the overall decrease in enthalpy is achieved by the generation of heat.

Conversely, for a constant-pressure endothermic reaction, is positive and equal to the heat ''absorbed'' in the reaction.

From the definition of enthalpy as the enthalpy change at constant pressure is However, for most chemical reactions, the work term is much smaller than the internal energy change , which is approximately equal to . As an example, for the combustion of carbon monoxide and
Since the differences are so small, reaction enthalpies are often described as reaction energies and analyzed in terms of bond energies.

Specific enthalpy

The ''specific enthalpy'' of a uniform system is defined as , where is the mass of the system. Its SI unit is joule per kilogram. It can be expressed in other specific quantities by where is the specific internal energy, is the pressure, and is specific volume, which is equal to , where is the density.

Enthalpy changes

An enthalpy change describes the change in enthalpy observed in the constituents of a thermodynamic system when undergoing a transformation or chemical reaction. It is the difference between the enthalpy after the process has completed, i.e. the enthalpy of the products assuming that the reaction goes to completion, and the initial enthalpy of the system, namely the reactants. These processes are specified solely by their initial and final states, so that the enthalpy change for the reverse is the negative of that for the forward process.

A common standard enthalpy change is the enthalpy of formation, which has been determined for a large number of substances. Enthalpy changes are routinely measured and compiled in chemical and physical reference works, such as the CRC Handbook of Chemistry and Physics. The following is a selection of enthalpy changes commonly recognized in thermodynamics.

When used in these recognized terms the qualifier ''change'' is usually dropped and the property is simply termed ''enthalpy of "process"''. Since these properties are often used as reference values, it is very common to quote them for a standardized set of environmental parameters, or standard conditions, including:
* A pressure of one atmosphere (1 atm = 1013.25 hPa) or 1 bar
* A temperature of 25 °C = 298.15 K
* A concentration of 1.0  M when the element or compound is present in solution
* Elements or compounds in their normal physical states, i.e. standard state
For such standardized values the name of the enthalpy is commonly prefixed with the term ''standard'', e.g. ''standard enthalpy of formation''.

Chemical properties

Enthalpy of reaction is defined as the enthalpy change observed in a constituent of a thermodynamic system when one mole of substance reacts completely.

Enthalpy of formation is defined as the enthalpy change observed in a constituent of a thermodynamic system when one mole of a compound is formed from its elementary antecedents.

Enthalpy of combustion is defined as the enthalpy change observed in a constituent of a thermodynamic system when one mole of a substance burns completely with oxygen.

Enthalpy of hydrogenation is defined as the enthalpy change observed in a constituent of a thermodynamic system when one mole of an unsaturated compound reacts completely with an excess of hydrogen to form a saturated compound.

Enthalpy of atomization is defined as the enthalpy change required to separate one mole of a substance into its constituent atoms completely.

Enthalpy of neutralization is defined as the enthalpy change observed in a constituent of a thermodynamic system when one mole of water is formed when an acid and a base react.

Standard enthalpy of solution is defined as the enthalpy change observed in a constituent of a thermodynamic system when one mole of a solute is dissolved completely in an excess of solvent, so that the solution is at infinite dilution.

Standard enthalpy of denaturation is defined as the enthalpy change required to denature one mole of compound.

Enthalpy of hydration is defined as the enthalpy change observed when one mole of gaseous ions is completely dissolved in water forming one mole of aqueous ions.

Physical properties

Enthalpy of fusion is defined as the enthalpy change required to completely change the state of one mole of substance from solid to liquid.

Enthalpy of vaporization is defined as the enthalpy change required to completely change the state of one mole of substance from liquid to gas.

Enthalpy of sublimation is defined as the enthalpy change required to completely change the state of one mole of substance from solid to gas.

Lattice enthalpy is defined as the energy required to separate one mole of an ionic compound into separated gaseous ions to an infinite distance apart (meaning no force of attraction).

Enthalpy of mixing is defined as the enthalpy change upon mixing of two (non-reacting) chemical substances.

Open systems

In thermodynamic open systems, mass (of substances) may flow in and out of the system boundaries. The first law of thermodynamics for open systems states: The increase in the internal energy of a system is equal to the amount of energy added to the system by mass flowing in and by heating, minus the amount lost by mass flowing out and in the form of work done by the system:
$\mathrmU = \delta Q + \mathrmU_\text - \mathrmU_\text - \delta W,$
where is the average internal energy entering the system, and is the average internal energy leaving the system.

The region of space enclosed by the boundaries of the open system is usually called a control volume, and it may or may not correspond to physical walls. If we choose the shape of the control volume such that all flow in or out occurs perpendicular to its surface, then the flow of mass into the system performs work as if it were a piston of fluid pushing mass into the system, and the system performs work on the flow of mass out as if it were driving a piston of fluid. There are then two types of work performed: ''flow work'' described above, which is performed on the fluid (this is also often called '' work''), and ''mechanical work'' (''shaft work''), which may be performed on some mechanical device such as a turbine or pump.

These two types of work are expressed in the equation
$\delta W = \mathrm(p_\text V_\text) - \mathrm(p_\text V_\text) + \delta W_\text.$
Substitution into the equation above for the control volume (cv) yields
$\mathrmU_\text = \delta Q + \mathrmU_\text + \mathrm(p_\text V_\text) - \mathrmU_\text - \mathrm(p_\text V_\text) - \delta W_\text.$

The definition of enthalpy permits us to use this thermodynamic potential to account for both internal energy and work in fluids for open systems:
$\mathrmU_\text = \delta Q + \mathrmH_\text - \mathrmH_\text - \delta W_\text.$

If we allow also the system boundary to move (e.g. due to moving pistons), we get a rather general form of the first law for open systems.
In terms of time derivatives, using Newton's dot notation for time derivatives, it reads:
$\frac = \sum_k \dot Q_k + \sum_k \dot H_k - \sum_k p_k\frac - P,$
with sums over the various places where heat is supplied, mass flows into the system, and boundaries are moving. The terms represent enthalpy flows, which can be written as
$\dot H_k = h_k \dot m_k = H_\text \dot n_k,$
with $\dot m_k$ the mass flow and $\dot n_k$ the molar flow at position respectively. The term represents the rate of change of the system volume at position that results in power done by the system. The parameter represents all other forms of power done by the system such as shaft power, but it can also be, say, electric power produced by an electrical power plant.

Note that the previous expression holds true only if the kinetic energy flow rate is conserved between system inlet and outlet. Otherwise, it has to be included in the enthalpy balance. During steady-state operation of a device (see Turbine, Pump, and Engine), the average may be set equal to zero. This yields a useful expression for the average power generation for these devices in the absence of chemical reactions:
$P = \sum_k \big\langle \dot Q_k \big\rangle + \sum_k \big\langle \dot H_k \big\rangle - \sum_k \left\langle p_k \frac \right\rangle,$
where the angle brackets denote time averages. The technical importance of the enthalpy is directly related to its presence in the first law for open systems, as formulated above.

Diagrams

The enthalpy values of important substances can be obtained using commercial software. Practically all relevant material properties can be obtained either in tabular or in graphical form. There are many types of diagrams, such as diagrams, which give the specific enthalpy as function of temperature for various pressures, and diagrams, which give as function of for various . One of the most common diagrams is the temperature–specific entropy diagram ( diagram). It gives the melting curve and saturated liquid and vapor values together with isobars and isenthalps. These diagrams are powerful tools in the hands of the thermal engineer.

Some basic applications

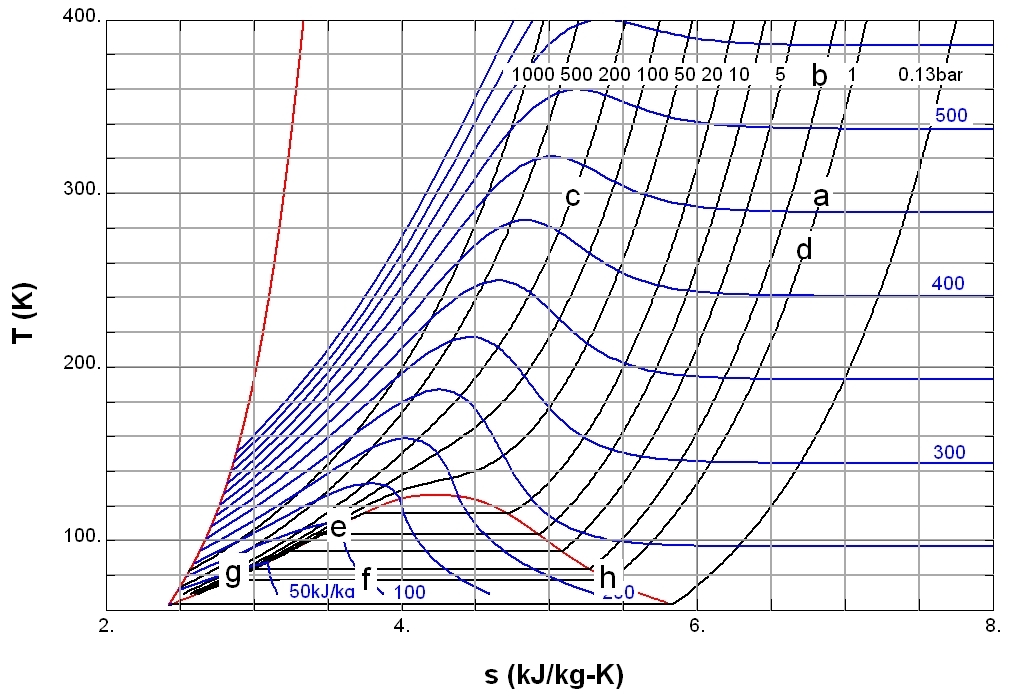
The points  through in the figure play a role in the discussion in this section.
:
Points  and are saturated liquids, and point  is a saturated gas.

Throttling

One of the simple applications of the concept of enthalpy is the so-called throttling process, also known as Joule–Thomson expansion. It concerns a steady adiabatic flow of a fluid through a flow resistance (valve, porous plug, or any other type of flow resistance) as shown in the figure. This process is very important, since it is at the heart of domestic refrigerators, where it is responsible for the temperature drop between ambient temperature and the interior of the refrigerator. It is also the final stage in many types of liquefiers.

For a steady state flow regime, the enthalpy of the system (dotted rectangle) has to be constant. Hence

$0 = \dot m h_1 - \dot m h_2 ~.$

Since the mass flow is constant, the specific enthalpies at the two sides of the flow resistance are the same:

$h_1 = h_2 \; ,$

that is, the enthalpy per unit mass does not change during the throttling. The consequences of this relation can be demonstrated using the diagram above.

Example 1

Point c is at 200 bar and room temperature (300 K). A Joule–Thomson expansion from 200 bar to 1 bar follows a curve of constant enthalpy of roughly 425  (not shown in the diagram) lying between the 400 and 450  isenthalps and ends in point d, which is at a temperature of about 270 K . Hence the expansion from 200 bar to 1 bar cools nitrogen from 300 K to 270 K . In the valve, there is a lot of friction, and a lot of entropy is produced, but still the final temperature is below the starting value.

Example 2

Point e is chosen so that it is on the saturated liquid line with It corresponds roughly with and Throttling from this point to a pressure of 1 bar ends in the two-phase region (point f). This means that a mixture of gas and liquid leaves the throttling valve. Since the enthalpy is an extensive parameter, the enthalpy in is equal to the enthalpy in multiplied by the liquid fraction in plus the enthalpy in multiplied by the gas fraction in So

$h_\mathbf\mathsf = x_\mathbf\mathsf h_\mathbf\mathsf + (1 - x_\mathbf\mathsf)h_\mathsf\mathbf ~.$

With numbers:
: so
This means that the mass fraction of the liquid in the liquid–gas mixture that leaves the throttling valve is 64%.

Compressors

A power is applied e.g. as electrical power. If the compression is adiabatic, the gas temperature goes up. In the reversible case it would be at constant entropy, which corresponds with a vertical line in the diagram. For example, compressing nitrogen from 1 bar (point a) to 2 bar (point b) would result in a temperature increase from 300 K to 380 K. In order to let the compressed gas exit at ambient temperature , heat exchange, e.g. by cooling water, is necessary. In the ideal case the compression is isothermal. The average heat flow to the surroundings is . Since the system is in the steady state the first law gives

$0 = -\dot Q + \dot m\, h_1 - \dot m\, h_2 + P ~.$

The minimal power needed for the compression is realized if the compression is reversible. In that case the second law of thermodynamics for open systems gives

$0 = -\frac + \dot m \, s_1 - \dot m \, s_2 ~.$

Eliminating gives for the minimal power

$\frac = h_2 - h_1 - T_\mathsf\left( s_2 - s_1 \right) ~.$

For example, compressing 1 kg of nitrogen from 1 bar to 200 bar costs at least :
With the data, obtained with the diagram, we find a value of

The relation for the power can be further simplified by writing it as

$\frac = \int_1^2 \left( \mathrmh - T_\mathsf\,\mathrms \right) ~.$

With
:
this results in the final relation

$\frac = \int_1^2 v\,\mathrmp ~.$

History and etymology

The term ''enthalpy'' was coined relatively late in the history of thermodynamics, in the early 20th century. Energy was introduced in a modern sense by Thomas Young in 1802, while entropy by Rudolf Clausius in 1865. ''Energy'' uses the root of the Greek word (''ergon''), meaning "work", to express the idea of capacity to perform work. ''Entropy'' uses the Greek word (''tropē'') meaning ''transformation'' or ''turning''. ''Enthalpy'' uses the root of the Greek word (''thalpos'') "warmth, heat".

The term expresses the obsolete concept of ''heat content'', as refers to the amount of heat gained in a process at constant pressure only, but not in the general case when pressure is variable. J. W. Gibbs used the term "a heat function for constant pressure" for clarity.

Introduction of the concept of "heat content" is associated with Benoît Paul Émile Clapeyron and Rudolf Clausius (Clausius–Clapeyron relation, 1850).

The term ''enthalpy'' first appeared in print in 1909. It is attributed to Heike Kamerlingh Onnes, who most likely introduced it orally the year before, at the first meeting of the Institute of Refrigeration in Paris. It gained currency only in the 1920s, notably with the '' Mollier Steam Tables and Diagrams'', published in 1927.

Until the 1920s, the symbol was used, somewhat inconsistently, for "heat" in general. The definition of as strictly limited to enthalpy or "heat content at constant pressure" was formally proposed by A. W. Porter in 1922.

.

Notes

See also

* Calorimetry
* Calorimeter
* Departure function
* Hess's law
* Isenthalpic process
* Laws of thermodynamics
* Stagnation enthalpy
* Standard enthalpy of formation
* Thermodynamic databases
* Thermodynamics

References

Bibliography

*
*
*
*
*
*
*
*

External links

*
*
*

{{Authority control

State functions
Energy (physics)
Physical quantities