Mild-slope equation

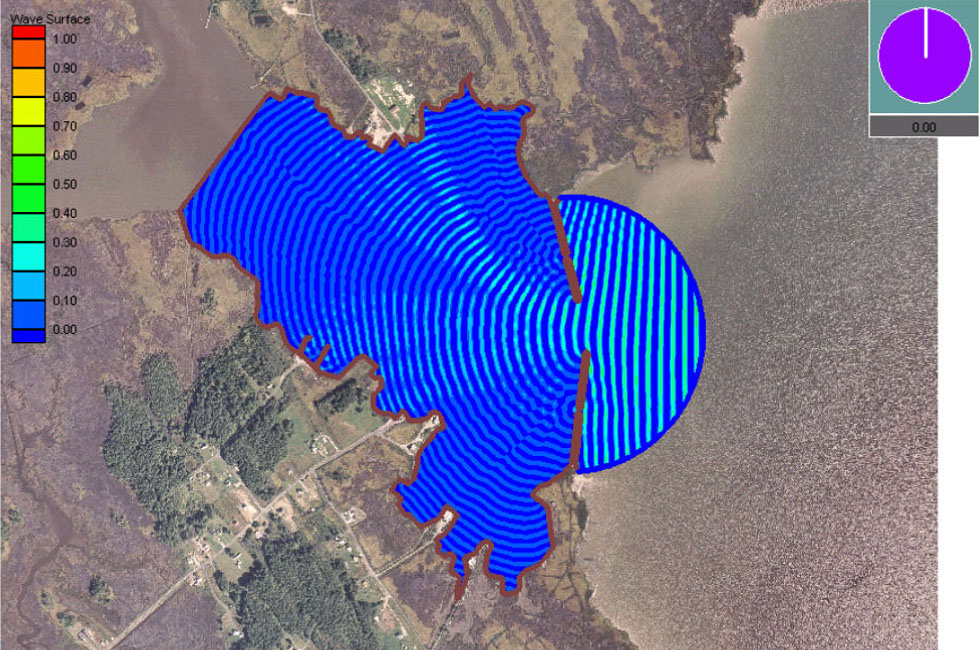In fluid dynamics, the mild-slope equation describes the combined effects of diffraction and refraction for water waves propagating over bathymetry and due to lateral boundaries—like breakwaters and coastlines. It is an approximate model, deriving its name from being originally developed for wave propagation over mild slopes of the sea floor. The mild-slope equation is often used in coastal engineering to compute the wave-field changes near harbours and coasts.

The mild-slope equation models the propagation and transformation of water waves, as they travel through waters of varying depth and interact with lateral boundaries such as cliffs, beaches, seawalls and breakwaters. As a result, it describes the variations in wave amplitude, or equivalently wave height. From the wave amplitude, the amplitude of the flow velocity oscillations underneath the water surface can also be computed. These quantities—wave amplitude and flow-velocity amplitude—may subsequently be used to determine the wave effects on coastal and offshore structures, ships and other floating objects, sediment transport and resulting bathymetric changes of the sea bed and coastline, mean flow fields and mass transfer of dissolved and floating materials. Most often, the mild-slope equation is solved by computer using methods from numerical analysis.

A first form of the mild-slope equation was developed by Eckart in 1952, and an improved version—the mild-slope equation in its classical formulation—has been derived independently by Juri Berkhoff in 1972. Thereafter, many modified and extended forms have been proposed, to include the effects of, for instance: wave–current interaction, wave nonlinearity, steeper sea-bed slopes, bed friction and wave breaking. Also parabolic approximations to the mild-slope equation are often used, in order to reduce the computational cost.

In case of a constant depth, the mild-slope equation reduces to the Helmholtz equation for wave diffraction.

Formulation for monochromatic wave motion

For monochromatic waves according to linear theory—with the free surface elevation given as $\zeta(x,y,t) = \Re\left\$ and the waves propagating on a fluid layer of mean water depth $h(x,y)$—the mild-slope equation is:
$\nabla\cdot\left( c_p\, c_g\, \nabla \eta \right)\, +\, k^2\, c_p\, c_g\, \eta\, =\, 0,$
where:
*$\eta(x,y)$ is the complex-valued amplitude of the free-surface elevation $\zeta(x,y,t);$
*$(x,y)$ is the horizontal position;
*$\omega$ is the angular frequency of the monochromatic wave motion;
*$i$ is the imaginary unit;
*$\Re\$ means taking the real part of the quantity between braces;
*$\nabla$ is the horizontal gradient operator;
*$\nabla\cdot$ is the divergence operator;
*$k$ is the wavenumber;
*$c_p$ is the phase speed of the waves and
*$c_g$ is the group speed of the waves.
The phase and group speed depend on the dispersion relation, and are derived from Airy wave theory as:

\begin
\omega^2 &=\, g\, k\, \tanh\, (kh), \\
c_p &=\, \frac \quad \text \\
c_g &=\, \frac 1 2 \, c_p\, \left 1\, +\, kh\, \frac \right\end
where
*$g$ is Earth's gravity and
*$\tanh$ is the hyperbolic tangent.
For a given angular frequency $\omega$, the wavenumber $k$ has to be solved from the dispersion equation, which relates these two quantities to the water depth $h$.

Transformation to an inhomogeneous Helmholtz equation

Through the transformation
$\psi\, =\, \eta\, \sqrt,$
the mild slope equation can be cast in the form of an inhomogeneous Helmholtz equation:
$\Delta\psi\, +\, k_c^2\, \psi\, =\, 0 \qquad \text \qquad k_c^2\, =\, k^2\, -\, \frac,$
where $\Delta$ is the Laplace operator.

Propagating waves

In spatially coherent fields of propagating waves, it is useful to split the complex amplitude $\eta(x,y)$ in its amplitude and phase, both real valued:
$\eta(x,y)\, =\, a(x,y) \, e^,$
where
*$a = , \eta, \,$ is the amplitude or absolute value of $\eta\,$ and
*$\theta = \arg\\,$ is the wave phase, which is the argument of $\eta.$

This transforms the mild-slope equation in the following set of equations (apart from locations for which $\nabla\theta$ is singular):

$\begin \frac\, -\, \frac\, =\, 0 \qquad &\text \kappa_x\, =\, \frac \text \kappa_y\, =\, \frac, \\ \kappa^2\, =\, k^2\, +\, \frac \qquad &\text \kappa\, =\, \sqrt \quad \text \\ \nabla \cdot \left( \boldsymbol_g\, E \right)\, =\, 0 \qquad &\text E\, =\, \frac 1 2\, \rho\, g\, a^2 \quad \text \quad \boldsymbol_g\, =\, c_g\, \frac, \end$
where
* $E$ is the average wave-energy density per unit horizontal area (the sum of the kinetic and potential energy densities),
* $\boldsymbol$ is the effective wavenumber vector, with components $(\kappa_x,\kappa_y),$
* $\boldsymbol_g$ is the effective group velocity vector,
* $\rho$ is the fluid density, and
* $g$ is the acceleration by the Earth's gravity.

The last equation shows that wave energy is conserved in the mild-slope equation, and that the wave energy $E$ is transported in the $\boldsymbol$-direction normal to the wave crests (in this case of pure wave motion without mean currents). The effective group speed $, \boldsymbol_g,$ is different from the group speed $c_g.$

The first equation states that the effective wavenumber $\boldsymbol$ is irrotational, a direct consequence of the fact it is the derivative of the wave phase $\theta$, a scalar field. The second equation is the eikonal equation. It shows the effects of diffraction on the effective wavenumber: only for more-or-less progressive waves, with $\left, \nabla\cdot(c_p\, c_g\, \nabla a)\ \ll k^2\, c_p\, c_g\, a,$ the splitting into amplitude $a$ and phase $\theta$ leads to consistent-varying and meaningful fields of $a$ and $\boldsymbol$. Otherwise, ''κ''² can even become negative. When the diffraction effects are totally neglected, the effective wavenumber ''κ'' is equal to $k$, and the geometric optics approximation for wave refraction can be used.

When $\eta=a\,\exp(i\theta)$ is used in the mild-slope equation, the result is, apart from a factor $\exp(i\theta)$:

$c_p\,c_g\, \left( \Delta a\, +\, 2i\, \nabla a \cdot \nabla\theta\, -\, a\, \nabla\theta \cdot \nabla\theta\, +\, i\, a\, \Delta\theta \right)\, +\, \nabla \left( c_p\, c_g \right) \cdot \left( \nabla a\, +\, i\, a\, \nabla\theta \right)\, +\, k^2\, c_p\, c_g\, a\, =\, 0.$

Now both the real part and the imaginary part of this equation have to be equal to zero:
$\begin & c_p\,c_g\, \Delta a\, -\, c_p\, c_g\, a\, \nabla\theta \cdot \nabla\theta\, +\, \nabla \left( c_p\, c_g \right) \cdot \nabla a\, +\, k^2\, c_p\, c_g\, a\, =\, 0 \quad \text \\ & 2\, c_p\,c_g\, \nabla a \cdot \nabla\theta\, +\, c_p\, c_g\, a\, \Delta\theta\, +\, \nabla \left( c_p\, c_g \right) \cdot \left( a\, \nabla\theta \right)\, =\, 0. \end$

The effective wavenumber vector $\boldsymbol$ is ''defined'' as the gradient of the wave phase:
$\boldsymbol = \nabla\theta$ and its vector length is $\kappa = , \boldsymbol, .$

Note that $\boldsymbol$ is an irrotational field, since the curl of the gradient is zero:
$\nabla \times \boldsymbol = 0.$

Now the real and imaginary parts of the transformed mild-slope equation become, first multiplying the imaginary part by $a$:
$\begin &\kappa^2\, =\, k^2\, +\, \frac \cdot \frac\, +\, \frac \quad \text \\ &c_p\, c_g\, \nabla\left(a^2\right) \cdot \boldsymbol\, +\, c_p\, c_g\, \nabla\cdot\boldsymbol\, +\, a^2\, \boldsymbol \cdot \nabla \left( c_p\, c_g \right)\, =\, 0. \end$

The first equation directly leads to the eikonal equation above for $\kappa\,$, while the second gives:
$\nabla \cdot \left( \boldsymbol\, c_p\, c_g\, a^2 \right)\, =\, 0,$

which—by noting that $c_p = \omega / k$ in which the angular frequency $\omega$ is a constant for time-harmonic motion—leads to the wave-energy conservation equation.

Derivation of the mild-slope equation

The mild-slope equation can be derived by the use of several methods. Here, we will use a variational approach. The fluid is assumed to be inviscid and incompressible, and the flow is assumed to be irrotational. These assumptions are valid ones for surface gravity waves, since the effects of vorticity and viscosity are only significant in the Stokes boundary layers (for the oscillatory part of the flow). Because the flow is irrotational, the wave motion can be described using potential flow theory.

Luke's variational principle

Luke's Lagrangian formulation gives a variational formulation for non-linear surface gravity waves.
For the case of a horizontally unbounded domain with a constant density $\rho$, a free fluid surface at $z=\zeta(x,y,t)$ and a fixed sea bed at $z=-h(x,y),$ Luke's variational principle $\delta\mathcal=0$ uses the Lagrangian
$\mathcal = \int_^ \iint L\, \textx\, \texty\, \textt,$
where $L$ is the horizontal Lagrangian density, given by:
$L = -\rho\, \left\,$

where $\Phi(x,y,z,t)$ is the velocity potential, with the flow velocity components being $\partial\Phi/\partial,$ $\partial\Phi / \partial$ and $\partial\Phi / \partial$ in the $x$, $y$ and $z$ directions, respectively.
Luke's Lagrangian formulation can also be recast into a Hamiltonian formulation in terms of the surface elevation and velocity potential at the free surface.
Taking the variations of $\mathcal(\Phi,\zeta)$ with respect to the potential $\Phi(x,y,z,t)$ and surface elevation $\zeta(x,y,t)$ leads to the Laplace equation for $\Phi$ in the fluid interior, as well as all the boundary conditions both on the free surface $z=\zeta(x,y,t)$ as at the bed at $z=-h(x,y).$

Linear wave theory

In case of linear wave theory, the vertical integral in the Lagrangian density $L$ is split into a part from the bed $z=-h$ to the mean surface at $z=0,$ and a second part from $z=0$ to the free surface $z=\zeta$. Using a Taylor series expansion for the second integral around the mean free-surface elevation $z=0,$ and only retaining quadratic terms in $\Phi$ and $\zeta,$ the Lagrangian density $L_0$ for linear wave motion becomes
$L_0 = -\rho\, \left\.$

The term $\partial\Phi/\partial$ in the vertical integral is dropped since it has become dynamically uninteresting: it gives a zero contribution to the Euler–Lagrange equations, with the upper integration limit now fixed. The same is true for the neglected bottom term proportional to $h^2$ in the potential energy.

The waves propagate in the horizontal $(x,y)$ plane, while the structure of the potential $\Phi$ is not wave-like in the vertical $z$-direction. This suggests the use of the following assumption on the form of the potential $\Phi:$
$\Phi(x,y,z,t) = f(z;x,y) \, \varphi(x,y,t)$ with normalisation $f(0;x,y) = 1$ at the mean free-surface elevation $z=0.$

Here $\varphi(x,y,t)$ is the velocity potential at the mean free-surface level $z=0.$ Next, the mild-slope assumption is made, in that the vertical shape function $f$ changes slowly in the $(x,y)$-plane, and horizontal derivatives of $f$ can be neglected in the flow velocity. So:

\begin
\dfrac \\ ex \dfrac \\ ex \dfrac
\end\,
\approx\,
\begin
f \dfrac \\ ex f \dfrac \\ ex \dfrac\, \varphi
\end.

As a result:
$L_0 = -\rho \left\,$ with $\begin F &= \int_^0 f^2\, \textz \\ G &= \int_^0 \left(\frac\right)^2 \textz. \end$

The Euler–Lagrange equations for this Lagrangian density $L_0$ are, with $\xi(x,y,t)$ representing either $\varphi$ or $\zeta:$
$\frac - \frac\left( \frac \right) - \frac\left( \frac \right) - \frac\left( \frac \right) = 0.$

Now $\xi$ is first taken equal to $\varphi$ and then to $\zeta.$
As a result, the evolution equations for the wave motion become:
$\begin \frac\, &+ \nabla \cdot \left( F\, \nabla\varphi \right) - G \varphi = 0 \quad \text \\ \frac\, &+\, g \zeta = 0, \end$
with the horizontal gradient operator: where superscript denotes the transpose.

The next step is to choose the shape function $f$ and to determine $F$ and $G.$

Vertical shape function from Airy wave theory

Since the objective is the description of waves over mildly sloping beds, the shape function $f(z)$ is chosen according to Airy wave theory. This is the linear theory of waves propagating in constant depth $h.$ The form of the shape function is:
$f = \frac,$
with $k(x,y)$ now in general not a constant, but chosen to vary with $x$ and $y$ according to the local depth $h(x,y)$ and the linear dispersion relation:
$\omega_0^2 = g k \tanh (k h).$

Here $\omega_0$ a constant angular frequency, chosen in accordance with the characteristics of the wave field under study. Consequently, the integrals $F$ and $G$ become:
$\begin F &= \int_h^0 f^2\, \textz = \frac c_p c_g \quad \text \\ G &= \int_h^0 \left( \frac \right)^2 \textz = \frac \left( \omega_0^2 - k^2 c_p c_g \right). \end$

The following time-dependent equations give the evolution of the free-surface elevation $\zeta(x,y,t)$ and free-surface potential $\phi(x,y,t):$
$\begin g\, \frac &+ \nabla\cdot\left( c_p c_g\, \nabla \varphi \right) + \left( k^2 c_p c_g - \omega_0^2 \right) \varphi = 0, \\ \frac &+ g \zeta = 0, \quad \text \quad \omega_0^2 = g k \tanh (kh). \end$

From the two evolution equations, one of the variables $\varphi$ or $\zeta$ can be eliminated, to obtain the time-dependent form of the mild-slope equation:
$-\frac + \nabla\cdot\left( c_p c_g\, \nabla \zeta \right) + \left( k^2 c_p c_g - \omega_0^2 \right) \zeta = 0,$
and the corresponding equation for the free-surface potential is identical, with $\zeta$ replaced by $\varphi.$ The time-dependent mild-slope equation can be used to model waves in a narrow band of frequencies around $\omega_0.$

Monochromatic waves

Consider monochromatic waves with complex amplitude $\eta(x,y)$ and angular frequency $\omega$:
$\zeta(x,y,t) = \Re\left\,$
with $\omega$ and $\omega_0$ chosen equal to each other, $\omega = \omega_0.$ Using this in the time-dependent form of the mild-slope equation, recovers the classical mild-slope equation for time-harmonic wave motion:
$\nabla \cdot \left( c_p\, c_g\, \nabla \eta \right)\, +\, k^2\, c_p\, c_g\, \eta\, =\, 0.$

Applicability and validity of the mild-slope equation

The standard mild slope equation, without extra terms for bed slope and bed curvature, provides accurate results for the wave field over bed slopes ranging from 0 to about 1/3. However, some subtle aspects, like the amplitude of reflected waves, can be completely wrong, even for slopes going to zero. This mathematical curiosity has little practical importance in general since this reflection becomes vanishingly small for small bottom slopes.

Notes

References

*, 2 Parts, 967 pages.
*
*, 740 pages.
*
*

{{physical oceanography

Coastal geography
Equations of fluid dynamics
Water waves