Mandelbulb on:
[Wikipedia]
[Google]
[Amazon]
The Mandelbulb is a three-dimensional

 Another way to create Mandelbulbs with cubic symmetry is by taking the complex iteration formula for some
Another way to create Mandelbulbs with cubic symmetry is by taking the complex iteration formula for some 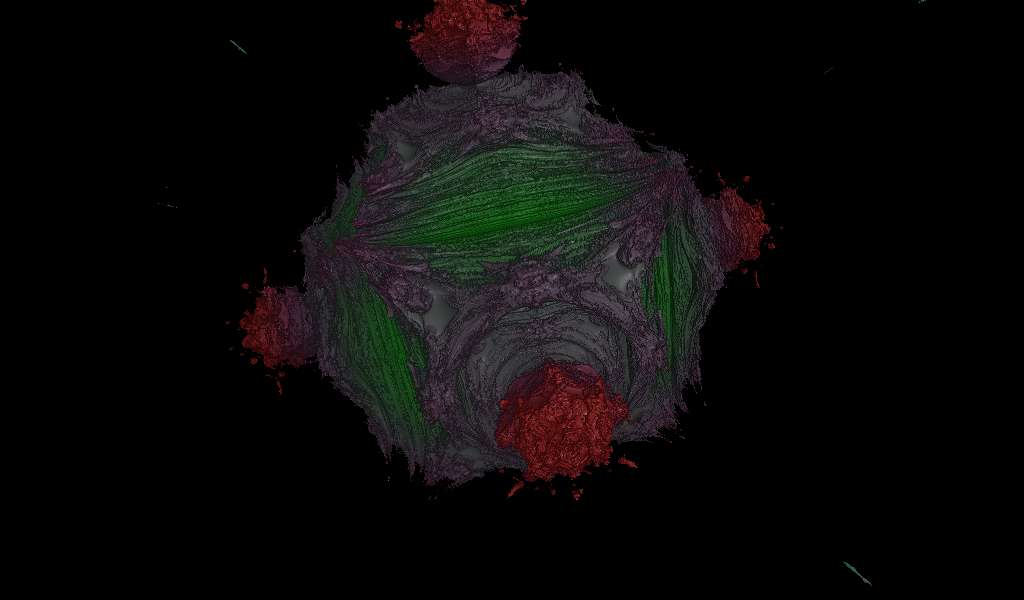
 This fractal has cross-sections of the power-9 Mandelbrot fractal. It has 32 small bulbs sprouting from the main sphere. It is defined by, for example,
:
:
:
These formula can be written in a shorter way:
:
and equivalently for the other coordinates.
This fractal has cross-sections of the power-9 Mandelbrot fractal. It has 32 small bulbs sprouting from the main sphere. It is defined by, for example,
:
:
:
These formula can be written in a shorter way:
:
and equivalently for the other coordinates.

for the first use of the Mandelbulb formula on www.fractal.org website Jules Ruis
* ttp://www.bugman123.com/Hypercomplex/index.html Several variants of the Mandelbulb, on Paul Nylander's website
An opensource fractal renderer that can be used to create images of the Mandelbulb
Formula for Mandelbulb/Juliabulb/Juliusbulb by Jules Ruis
Mandelbulb/Juliabulb/Juliusbulb with examples of real 3D objects
Video : View of the Mandelbulb
The discussion thread in Fractalforums.com that led to the Mandelbulb
Video fly through of an animated Mandelbulb world
Open-source Mandelbulber v2 software - Explore trigonometric, hyper-complex, Mandelbox, IFS, and many other 3D fractals.
Silent video: Explore the Mandelbulb (2024 rendering)
{{Mathematical art Fractals
fractal
In mathematics, a fractal is a Shape, geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scale ...
, constructed for the first time in 1997 by Jules Ruis and further developed in 2009 by Daniel White and Paul Nylander using spherical coordinates
In mathematics, a spherical coordinate system specifies a given point in three-dimensional space by using a distance and two angles as its three coordinates. These are
* the radial distance along the line connecting the point to a fixed point ...
.
A canonical
The adjective canonical is applied in many contexts to mean 'according to the canon' the standard, rule or primary source that is accepted as authoritative for the body of knowledge or literature in that context. In mathematics, ''canonical exampl ...
3-dimensional Mandelbrot set
The Mandelbrot set () is a two-dimensional set (mathematics), set that is defined in the complex plane as the complex numbers c for which the function f_c(z)=z^2+c does not Stability theory, diverge to infinity when Iteration, iterated starting ...
does not exist, since there is no 3-dimensional analogue of the 2-dimensional space of complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s. It is possible to construct Mandelbrot sets in 4 dimensions using quaternion
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quater ...
s and bicomplex numbers.
White and Nylander's formula for the "''n''th power" of the vector in is
:
where
:
:
:
The Mandelbulb is then defined as the set of those in for which the orbit of under the iteration is bounded. For ''n'' > 3, the result is a 3-dimensional bulb-like structure with fractal
In mathematics, a fractal is a Shape, geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scale ...
surface detail and a number of "lobes" depending on ''n''. Many of their graphic renderings use ''n'' = 8. However, the equations can be simplified into rational polynomials when ''n'' is odd. For example, in the case ''n'' = 3, the third power can be simplified into the more elegant form:
:
The Mandelbulb given by the formula above is actually one in a family of fractals given by parameters (''p'', ''q'') given by
:
Since ''p'' and ''q'' do not necessarily have to equal ''n'' for the identity , ''vn'', = , ''v'', ''n'' to hold, more general fractals can be found by setting
:
for functions ''f'' and ''g''.
Cubic formula
Other formula come from identities parametrising the sum of squares to give a power of the sum of squares, such as : which we can think of as a way to cube a triplet of numbers so that the modulus is cubed. So this gives, for example, : : : or other permutations. This reduces to the complex fractal when ''z'' = 0 and when ''y'' = 0. There are several ways to combine two such "cubic" transforms to get a power-9 transform, which has slightly more structure.Quintic formula

 Another way to create Mandelbulbs with cubic symmetry is by taking the complex iteration formula for some
Another way to create Mandelbulbs with cubic symmetry is by taking the complex iteration formula for some integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
''m'' and adding terms to make it symmetrical in 3 dimensions but keeping the cross-sections to be the same 2-dimensional fractal. (The 4 comes from the fact that .) For example, take the case of . In two dimensions, where , this is
:
:
This can be then extended to three dimensions to give
:
:
:
for arbitrary constants ''A'', ''B'', ''C'' and ''D'', which give different Mandelbulbs (usually set to 0). The case gives a Mandelbulb most similar to the first example, where ''n'' = 9. A more pleasing result for the fifth power is obtained by basing it on the formula .

Power-nine formula
 This fractal has cross-sections of the power-9 Mandelbrot fractal. It has 32 small bulbs sprouting from the main sphere. It is defined by, for example,
:
:
:
These formula can be written in a shorter way:
:
and equivalently for the other coordinates.
This fractal has cross-sections of the power-9 Mandelbrot fractal. It has 32 small bulbs sprouting from the main sphere. It is defined by, for example,
:
:
:
These formula can be written in a shorter way:
:
and equivalently for the other coordinates.

Spherical formula
A perfect spherical formula can be defined as a formula : where : where ''f'', ''g'' and ''h'' are ''n''th-power rational trinomials and ''n'' is an integer. The cubic fractal above is an example.Uses in media
* In the 2014 animated film '' Big Hero 6'', the climax takes place in the middle of awormhole
A wormhole is a hypothetical structure that connects disparate points in spacetime. It can be visualized as a tunnel with two ends at separate points in spacetime (i.e., different locations, different points in time, or both). Wormholes are base ...
, which is represented by the stylized interior of a Mandelbulb.
* In the 2018 science fiction
Science fiction (often shortened to sci-fi or abbreviated SF) is a genre of speculative fiction that deals with imaginative and futuristic concepts. These concepts may include information technology and robotics, biological manipulations, space ...
horror film
Horror is a film genre that seeks to elicit physical or psychological fear in its viewers. Horror films often explore dark subject matter and may deal with Transgressive art, transgressive topics or themes. Broad elements of the genre include Mo ...
''Annihilation
In particle physics, annihilation is the process that occurs when a subatomic particle collides with its respective antiparticle to produce other particles, such as an electron colliding with a positron to produce two photons. The total energy a ...
'', an extraterrestrial being appears in the form of a partial Mandelbulb.
* In the webcomic
Webcomics (also known as online comics or Internet comics) are comics published on the internet, such as on a website or a mobile app. While many webcomics are published exclusively online, others are also published in magazines, newspapers, or ...
''Unsounded'' the spirit realm of the khert is represented by a stylized golden mandelbulb.
* In the 2013-2020 drama show Marvel's Agents of S.H.I.E.L.D, season 7, episode 13, "What We're Fighting For", the beginning shows the S.H.I.E.L.D. team travel through the Quantum Realm whose opening appearance from the outside resembles the end of an internally rotating mandelbulb.
* In the 2016 film Marvel's Doctor Strange, one of the dimensions Strange is shown by the Ancient One depicts the top end of an expanding mandelbulb.
* In the 2020 film 2067, as the main character is arriving in the future, the distorted land he descends upon resembles a distorted and morphing mandelbulb.
See also
*Mandelbox
In mathematics, the mandelbox is a fractal with a boxlike shape found by Tom Lowe in 2010. It is defined in a similar way to the famous Mandelbrot set as the values of a parameter such that the origin does not escape to infinity under iteration ...
* List of fractals by Hausdorff dimension
According to Benoit Mandelbrot, "A fractal is by definition a set for which the Hausdorff-Besicovitch dimension strictly exceeds the topological dimension."
Presented here is a list of fractals, ordered by increasing Hausdorff dimension, to ill ...
References
6. http://www.fractal.org the Fractal Navigator by Jules RuisExternal links
for the first use of the Mandelbulb formula on www.fractal.org website Jules Ruis
* ttp://www.bugman123.com/Hypercomplex/index.html Several variants of the Mandelbulb, on Paul Nylander's website
An opensource fractal renderer that can be used to create images of the Mandelbulb
Formula for Mandelbulb/Juliabulb/Juliusbulb by Jules Ruis
Mandelbulb/Juliabulb/Juliusbulb with examples of real 3D objects
Video : View of the Mandelbulb
The discussion thread in Fractalforums.com that led to the Mandelbulb
Video fly through of an animated Mandelbulb world
Open-source Mandelbulber v2 software - Explore trigonometric, hyper-complex, Mandelbox, IFS, and many other 3D fractals.
Silent video: Explore the Mandelbulb (2024 rendering)
{{Mathematical art Fractals