Majorization on:
[Wikipedia]
[Google]
[Amazon]
In
 For we have if and only if is in the convex hull of all vectors obtained by permuting the coordinates of . This is equivalent to saying that for some
For we have if and only if is in the convex hull of all vectors obtained by permuting the coordinates of . This is equivalent to saying that for some 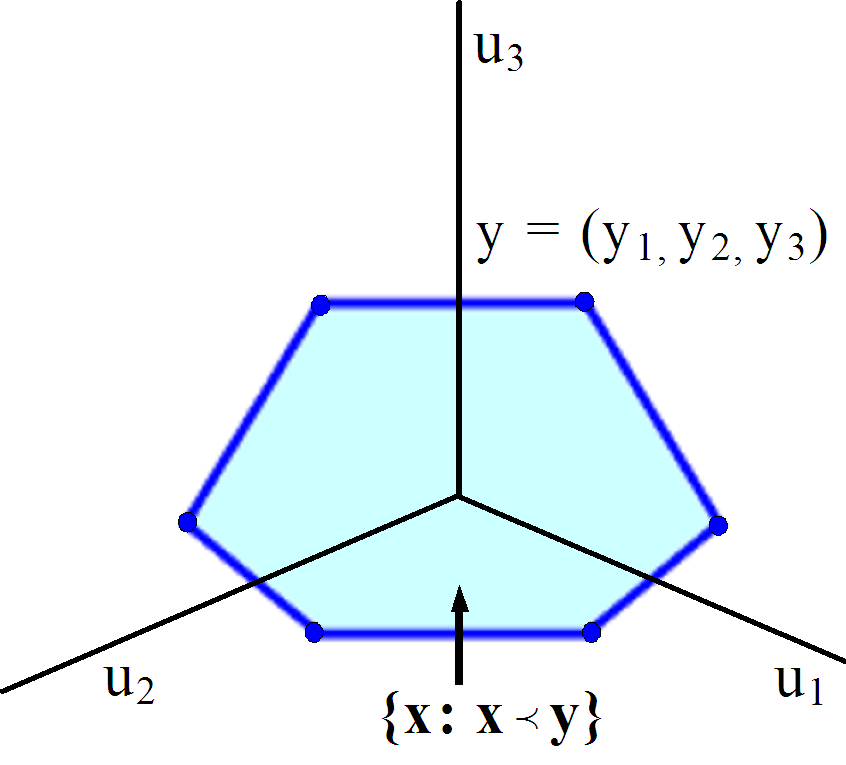
 Each vector can be plotted as a concave curve by connecting . Then is equivalent to the curve of being higher than that of .
Each vector can be plotted as a concave curve by connecting . Then is equivalent to the curve of being higher than that of .
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, majorization is a preorder
In mathematics, especially in order theory, a preorder or quasiorder is a binary relation that is reflexive relation, reflexive and Transitive relation, transitive. The name is meant to suggest that preorders are ''almost'' partial orders, ...
on vectors of real numbers
In mathematics, a real number is a number that can be used to measurement, measure a continuous variable, continuous one-dimensional quantity such as a time, duration or temperature. Here, ''continuous'' means that pairs of values can have arbi ...
. For two such vectors, , we say that weakly majorizes (or dominates) from below, commonly denoted when
: for all ,
where denotes th largest entry of . If further satisfy , we say that majorizes (or dominates) , commonly denoted .
Both weak majorization and majorization are partial orders for vectors whose entries are non-decreasing, but only a preorder
In mathematics, especially in order theory, a preorder or quasiorder is a binary relation that is reflexive relation, reflexive and Transitive relation, transitive. The name is meant to suggest that preorders are ''almost'' partial orders, ...
for general vectors, since majorization is agnostic to the ordering of the entries in vectors, e.g., the statement is simply equivalent to .
Specifically, if and only if are permutations of each other. Similarly for .
Majorizing also sometimes refers to entrywise ordering, e.g. the real-valued function ''f'' majorizes the real-valued function ''g'' when for all in the domain, or other technical definitions, such as majorizing measures in probability theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expre ...
.
Equivalent conditions
Geometric definition
 For we have if and only if is in the convex hull of all vectors obtained by permuting the coordinates of . This is equivalent to saying that for some
For we have if and only if is in the convex hull of all vectors obtained by permuting the coordinates of . This is equivalent to saying that for some doubly stochastic matrix
In mathematics, especially in probability and combinatorics, a doubly stochastic matrix
(also called bistochastic matrix) is a square matrix X=(x_) of nonnegative real numbers, each of whose rows and columns sums to 1, i.e.,
:\sum_i x_=\sum_j x_ ...
.Barry C. Arnold. "Majorization and the Lorenz Order: A Brief Introduction". Springer-Verlag Lecture Notes in Statistics, vol. 43, 1987. In particular, can be written as a convex combination
In convex geometry and Vector space, vector algebra, a convex combination is a linear combination of point (geometry), points (which can be vector (geometric), vectors, scalar (mathematics), scalars, or more generally points in an affine sp ...
of permutations of . In other words, is in the permutahedron
In mathematics, the permutohedron (also spelled permutahedron) of order is an -dimensional polytope embedded in an -dimensional space. Its vertex (geometry), vertex coordinates (labels) are the permutations of the first natural numbers. The edg ...
of .
Figure 1 displays the convex hull in 2D for the vector . Notice that the center of the convex hull, which is an interval in this case, is the vector . This is the "smallest" vector satisfying for this given vector .
Figure 2 shows the convex hull in 3D. The center of the convex hull, which is a 2D polygon in this case, is the "smallest" vector satisfying for this given vector .

Other definitions
Each of the following statements is true if and only if . * From we can produce by a finite sequence of "Robin Hood operations" where we replace two elements and with and , respectively, for some . * For every convex function , . **In fact, a special case suffices: and, for every , . *For every , . *Examples
Among non-negative vectors with three components, and permutations of it majorize all other vectors such that . For example, . Similarly, is majorized by all other such vectors, so . This behavior extends to general-lengthprobability vector
In mathematics and statistics, a probability vector or stochastic vector is a vector with non-negative entries that add up to one.
The positions (indices) of a probability vector represent the possible outcomes of a discrete random variable, and ...
s: the singleton vector majorizes all other probability vectors, and the uniform distribution is majorized by all probability vectors.
Schur convexity
A function is said to be Schur convex when implies . Hence, Schur-convex functions translate the ordering of vectors to a standard ordering in . Similarly, is Schur concave when implies An example of a Schur-convex function is the max function, . Schur convex functions are necessarily symmetric that the entries of it argument can be switched without modifying the value of the function. Therefore, linear functions, which are convex, are not Schur-convex unless they are symmetric. If a function is symmetric and convex, then it is Schur-convex.Generalizations
Majorization can be generalized to the Lorenz ordering, a partial order on distribution functions. For example, awealth distribution
The distribution of wealth is a comparison of the wealth of various members or groups in a society. It shows one aspect of economic inequality or economic heterogeneity.
The distribution of wealth differs from the income distribution in that ...
is Lorenz-greater than another if its Lorenz curve
In economics, the Lorenz curve is a graphical representation of the distribution of income or of wealth. It was developed by Max O. Lorenz in 1905 for representing Economic inequality, inequality of the wealth distribution.
The curve is a graph ...
lies below the other. As such, a Lorenz-greater wealth distribution has a higher Gini coefficient
In economics, the Gini coefficient ( ), also known as the Gini index or Gini ratio, is a measure of statistical dispersion intended to represent the income distribution, income inequality, the wealth distribution, wealth inequality, or the ...
, and has more income disparity
In economics, income distribution covers how a country's total GDP is distributed amongst its population. Economic theory and economic policy have long seen income and its distribution as a central concern. Unequal distribution of income causes e ...
.
The majorization preorder can be naturally extended to density matrices
In quantum mechanics, a density matrix (or density operator) is a matrix used in calculating the probabilities of the outcomes of measurements performed on physical systems. It is a generalization of the state vectors or wavefunctions: while th ...
in the context of quantum information
Quantum information is the information of the state of a quantum system. It is the basic entity of study in quantum information theory, and can be manipulated using quantum information processing techniques. Quantum information refers to both t ...
. In particular, exactly when