Logistic Regression on:
[Wikipedia]
[Google]
[Amazon]
 In statistics, the logistic model (or logit model) is a statistical model that models the
In statistics, the logistic model (or logit model) is a statistical model that models the
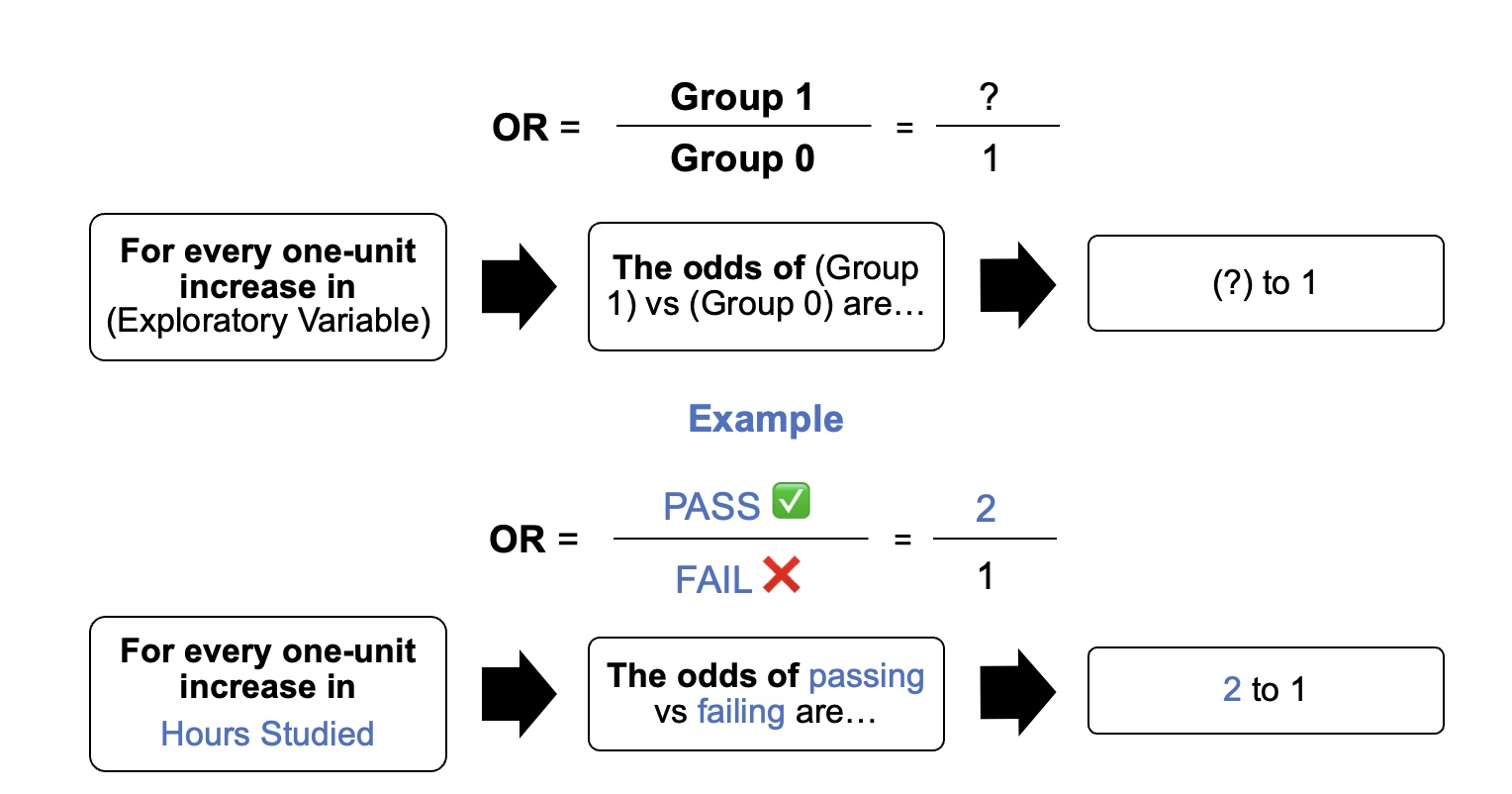
 As a simple example, we can use a logistic regression with one explanatory variable and two categories to answer the following question:
As a simple example, we can use a logistic regression with one explanatory variable and two categories to answer the following question:
 The logistic function is of the form:
:
where ''μ'' is a
The logistic function is of the form:
:
where ''μ'' is a
 This exponential relationship provides an interpretation for : The odds multiply by for every 1-unit increase in x.
For a binary independent variable the odds ratio is defined as where ''a'', ''b'', ''c'' and ''d'' are cells in a 2×2 contingency table.
This exponential relationship provides an interpretation for : The odds multiply by for every 1-unit increase in x.
For a binary independent variable the odds ratio is defined as where ''a'', ''b'', ''c'' and ''d'' are cells in a 2×2 contingency table.
probability
Probability is the branch of mathematics concerning numerical descriptions of how likely an event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speakin ...
of an event taking place by having the log-odds for the event be a linear combination of one or more independent variables. In regression analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one ...
, logistic regression (or logit regression) is estimating
Estimation (or estimating) is the process of finding an estimate or approximation, which is a value that is usable for some purpose even if input data may be incomplete, uncertain, or unstable. The value is nonetheless usable because it is der ...
the parameters of a logistic model (the coefficients in the linear combination). Formally, in binary logistic regression there is a single binary
Binary may refer to:
Science and technology Mathematics
* Binary number, a representation of numbers using only two digits (0 and 1)
* Binary function, a function that takes two arguments
* Binary operation, a mathematical operation that ta ...
dependent variable, coded by an indicator variable
In regression analysis, a dummy variable (also known as indicator variable or just dummy) is one that takes the values 0 or 1 to indicate the absence or presence of some categorical effect that may be expected to shift the outcome. For example, i ...
, where the two values are labeled "0" and "1", while the independent variables can each be a binary variable (two classes, coded by an indicator variable) or a continuous variable (any real value). The corresponding probability of the value labeled "1" can vary between 0 (certainly the value "0") and 1 (certainly the value "1"), hence the labeling; the function that converts log-odds to probability is the logistic function, hence the name. The unit of measurement
A unit of measurement is a definite magnitude of a quantity, defined and adopted by convention or by law, that is used as a standard for measurement of the same kind of quantity. Any other quantity of that kind can be expressed as a multi ...
for the log-odds scale is called a ''logit
In statistics, the logit ( ) function is the quantile function associated with the standard logistic distribution. It has many uses in data analysis and machine learning, especially in data transformations.
Mathematically, the logit is the ...
'', from ''logistic unit'', hence the alternative names. See and for formal mathematics, and for a worked example.
Binary variables are widely used in statistics to model the probability of a certain class or event taking place, such as the probability of a team winning, of a patient being healthy, etc. (see ), and the logistic model has been the most commonly used model for binary regression
In statistics, specifically regression analysis, a binary regression estimates a relationship between one or more explanatory variables and a single output binary variable. Generally the probability of the two alternatives is modeled, instead of s ...
since about 1970. Binary variables can be generalized to categorical variables when there are more than two possible values (e.g. whether an image is of a cat, dog, lion, etc.), and the binary logistic regression generalized to multinomial logistic regression. If the multiple categories are ordered, one can use the ordinal logistic regression (for example the proportional odds ordinal logistic model). See for further extensions. The logistic regression model itself simply models probability of output in terms of input and does not perform statistical classification
In statistics, classification is the problem of identifying which of a set of categories (sub-populations) an observation (or observations) belongs to. Examples are assigning a given email to the "spam" or "non-spam" class, and assigning a diagn ...
(it is not a classifier), though it can be used to make a classifier, for instance by choosing a cutoff value and classifying inputs with probability greater than the cutoff as one class, below the cutoff as the other; this is a common way to make a binary classifier.
Analogous linear models for binary variables with a different sigmoid function
A sigmoid function is a mathematical function having a characteristic "S"-shaped curve or sigmoid curve.
A common example of a sigmoid function is the logistic function shown in the first figure and defined by the formula:
:S(x) = \frac = \ ...
instead of the logistic function (to convert the linear combination to a probability) can also be used, most notably the probit model
In statistics, a probit model is a type of regression where the dependent variable can take only two values, for example married or not married. The word is a portmanteau, coming from ''probability'' + ''unit''. The purpose of the model is to est ...
; see . The defining characteristic of the logistic model is that increasing one of the independent variables multiplicatively scales the odds of the given outcome at a ''constant'' rate, with each independent variable having its own parameter; for a binary dependent variable this generalizes the odds ratio
An odds ratio (OR) is a statistic that quantifies the strength of the association between two events, A and B. The odds ratio is defined as the ratio of the odds of A in the presence of B and the odds of A in the absence of B, or equivalently (due ...
. More abstractly, the logistic function is the natural parameter for the Bernoulli distribution
In probability theory and statistics, the Bernoulli distribution, named after Swiss mathematician Jacob Bernoulli,James Victor Uspensky: ''Introduction to Mathematical Probability'', McGraw-Hill, New York 1937, page 45 is the discrete probabi ...
, and in this sense is the "simplest" way to convert a real number to a probability. In particular, it maximizes entropy (minimizes added information), and in this sense makes the fewest assumptions of the data being modeled; see .
The parameters of a logistic regression are most commonly estimated by maximum-likelihood estimation (MLE). This does not have a closed-form expression, unlike linear least squares; see . Logistic regression by MLE plays a similarly basic role for binary or categorical responses as linear regression by ordinary least squares
In statistics, ordinary least squares (OLS) is a type of linear least squares method for choosing the unknown parameters in a linear regression model (with fixed level-one effects of a linear function of a set of explanatory variables) by the ...
(OLS) plays for scalar responses: it is a simple, well-analyzed baseline model; see for discussion. The logistic regression as a general statistical model was originally developed and popularized primarily by Joseph Berkson, beginning in , where he coined "logit"; see .
Applications
Logistic regression is used in various fields, including machine learning, most medical fields, and social sciences. For example, the Trauma and Injury Severity Score ( TRISS), which is widely used to predict mortality in injured patients, was originally developed by Boyd ' using logistic regression. Many other medical scales used to assess severity of a patient have been developed using logistic regression. Logistic regression may be used to predict the risk of developing a given disease (e.g.diabetes
Diabetes, also known as diabetes mellitus, is a group of metabolic disorders characterized by a high blood sugar level ( hyperglycemia) over a prolonged period of time. Symptoms often include frequent urination, increased thirst and increased ...
; coronary heart disease
Coronary artery disease (CAD), also called coronary heart disease (CHD), ischemic heart disease (IHD), myocardial ischemia, or simply heart disease, involves the reduction of blood flow to the heart muscle due to build-up of atherosclerotic pl ...
), based on observed characteristics of the patient (age, sex, body mass index, results of various blood tests, etc.). Another example might be to predict whether a Nepalese voter will vote Nepali Congress or Communist Party of Nepal or Any Other Party, based on age, income, sex, race, state of residence, votes in previous elections, etc. The technique can also be used in engineering
Engineering is the use of scientific principles to design and build machines, structures, and other items, including bridges, tunnels, roads, vehicles, and buildings. The discipline of engineering encompasses a broad range of more speciali ...
, especially for predicting the probability of failure of a given process, system or product. It is also used in marketing
Marketing is the process of exploring, creating, and delivering value to meet the needs of a target market in terms of goods and services; potentially including selection of a target audience; selection of certain attributes or themes to emph ...
applications such as prediction of a customer's propensity to purchase a product or halt a subscription, etc. In economics
Economics () is the social science that studies the production, distribution, and consumption of goods and services.
Economics focuses on the behaviour and interactions of economic agents and how economies work. Microeconomics analyzes ...
, it can be used to predict the likelihood of a person ending up in the labor force, and a business application would be to predict the likelihood of a homeowner defaulting on a mortgage
A mortgage loan or simply mortgage (), in civil law jurisdicions known also as a hypothec loan, is a loan used either by purchasers of real property to raise funds to buy real estate, or by existing property owners to raise funds for any ...
. Conditional random field
Conditional random fields (CRFs) are a class of statistical modeling methods often applied in pattern recognition and machine learning and used for structured prediction. Whereas a classifier predicts a label for a single sample without consid ...
s, an extension of logistic regression to sequential data, are used in natural language processing.
Example
Problem
 As a simple example, we can use a logistic regression with one explanatory variable and two categories to answer the following question:
As a simple example, we can use a logistic regression with one explanatory variable and two categories to answer the following question:
A group of 20 students spends between 0 and 6 hours studying for an exam. How does the number of hours spent studying affect the probability of the student passing the exam?The reason for using logistic regression for this problem is that the values of the dependent variable, pass and fail, while represented by "1" and "0", are not
cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality (size) of sets. The cardinality of a finite set is a natural number: the number of elements in the set. T ...
s. If the problem was changed so that pass/fail was replaced with the grade 0–100 (cardinal numbers), then simple regression analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one ...
could be used.
The table shows the number of hours each student spent studying, and whether they passed (1) or failed (0).
We wish to fit a logistic function to the data consisting of the hours studied (''xk'') and the outcome of the test (''yk'' =1 for pass, 0 for fail). The data points are indexed by the subscript ''k'' which runs from to . The ''x'' variable is called the " explanatory variable", and the ''y'' variable is called the " categorical variable" consisting of two categories: "pass" or "fail" corresponding to the categorical values 1 and 0 respectively.
Model
location parameter
In geography, location or place are used to denote a region (point, line, or area) on Earth's surface or elsewhere. The term ''location'' generally implies a higher degree of certainty than ''place'', the latter often indicating an entity with an ...
(the midpoint of the curve, where ) and ''s'' is a scale parameter
In probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions. The larger the scale parameter, the more spread out the distribution.
Definition
If a family o ...
. This expression may be rewritten as:
:
where and is known as the intercept (it is the ''vertical'' intercept or ''y''-intercept of the line ), and (inverse scale parameter or rate parameter): these are the ''y''-intercept and slope of the log-odds as a function of ''x''. Conversely, and .
Fit
The usual measure of goodness of fit for a logistic regression uses logistic loss (orlog loss
In information theory, the cross-entropy between two probability distributions p and q over the same underlying set of events measures the average number of bits needed to identify an event drawn from the set if a coding scheme used for the set is ...
), the negative log-likelihood
The likelihood function (often simply called the likelihood) represents the probability of random variable realizations conditional on particular values of the statistical parameters. Thus, when evaluated on a given sample, the likelihood functi ...
. For a given ''xk'' and ''yk'', write . The are the probabilities that the corresponding will be unity and are the probabilities that they will be zero (see Bernoulli distribution
In probability theory and statistics, the Bernoulli distribution, named after Swiss mathematician Jacob Bernoulli,James Victor Uspensky: ''Introduction to Mathematical Probability'', McGraw-Hill, New York 1937, page 45 is the discrete probabi ...
). We wish to find the values of and which give the "best fit" to the data. In the case of linear regression, the sum of the squared deviations of the fit from the data points (''yk''), the squared error loss, is taken as a measure of the goodness of fit, and the best fit is obtained when that function is ''minimized''.
The log loss for the ''k''-th point is:
:
The log loss can be interpreted as the "surprisal
In information theory, the information content, self-information, surprisal, or Shannon information is a basic quantity derived from the probability of a particular Event (probability theory), event occurring from a random variable. It can be tho ...
" of the actual outcome relative to the prediction , and is a measure of information content
In information theory, the information content, self-information, surprisal, or Shannon information is a basic quantity derived from the probability of a particular event occurring from a random variable. It can be thought of as an alternative wa ...
. Note that log loss is always greater than or equal to 0, equals 0 only in case of a perfect prediction (i.e., when and , or and ), and approaches infinity as the prediction gets worse (i.e., when and or and ), meaning the actual outcome is "more surprising". Since the value of the logistic function is always strictly between zero and one, the log loss is always greater than zero and less than infinity. Note that unlike in a linear regression, where the model can have zero loss at a point by passing through a data point (and zero loss overall if all points are on a line), in a logistic regression it is not possible to have zero loss at any points, since is either 0 or 1, but .
These can be combined into a single expression:
:
This expression is more formally known as the cross entropy
In information theory, the cross-entropy between two probability distributions p and q over the same underlying set of events measures the average number of bits needed to identify an event drawn from the set if a coding scheme used for the set is ...
of the predicted distribution from the actual distribution , as probability distributions on the two-element space of (pass, fail).
The sum of these, the total loss, is the overall negative log-likelihood , and the best fit is obtained for those choices of and for which is ''minimized''.
Alternatively, instead of ''minimizing'' the loss, one can ''maximize'' its inverse, the (positive) log-likelihood:
:
or equivalently maximize the likelihood function
The likelihood function (often simply called the likelihood) represents the probability of random variable realizations conditional on particular values of the statistical parameters. Thus, when evaluated on a given sample, the likelihood funct ...
itself, which is the probability that the given data set is produced by a particular logistic function:
:
This method is known as maximum likelihood estimation
In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of an assumed probability distribution, given some observed data. This is achieved by maximizing a likelihood function so that, under the assumed stati ...
.
Parameter estimation
Since ''ℓ'' is nonlinear in and , determining their optimum values will require numerical methods. Note that one method of maximizing ''ℓ'' is to require the derivatives of ''ℓ'' with respect to and to be zero: : : and the maximization procedure can be accomplished by solving the above two equations for and , which, again, will generally require the use of numerical methods. The values of and which maximize ''ℓ'' and ''L'' using the above data are found to be: : : which yields a value for ''μ'' and ''s'' of: : :Predictions
The and coefficients may be entered into the logistic regression equation to estimate the probability of passing the exam. For example, for a student who studies 2 hours, entering the value into the equation gives the estimated probability of passing the exam of 0.25: : : Similarly, for a student who studies 4 hours, the estimated probability of passing the exam is 0.87: : : This table shows the estimated probability of passing the exam for several values of hours studying.Model evaluation
The logistic regression analysis gives the following output. By theWald test
In statistics, the Wald test (named after Abraham Wald) assesses constraints on statistical parameters based on the weighted distance between the unrestricted estimate and its hypothesized value under the null hypothesis, where the weight is the ...
, the output indicates that hours studying is significantly associated with the probability of passing the exam (). Rather than the Wald method, the recommended method to calculate the ''p''-value for logistic regression is the likelihood-ratio test
In statistics, the likelihood-ratio test assesses the goodness of fit of two competing statistical models based on the ratio of their likelihoods, specifically one found by maximization over the entire parameter space and another found after im ...
(LRT), which for this data gives (see below).
Generalizations
This simple model is an example of binary logistic regression, and has one explanatory variable and a binary categorical variable which can assume one of two categorical values. Multinomial logistic regression is the generalization of binary logistic regression to include any number of explanatory variables and any number of categories.Background
Definition of the logistic function
An explanation of logistic regression can begin with an explanation of the standard logistic function. The logistic function is asigmoid function
A sigmoid function is a mathematical function having a characteristic "S"-shaped curve or sigmoid curve.
A common example of a sigmoid function is the logistic function shown in the first figure and defined by the formula:
:S(x) = \frac = \ ...
, which takes any real
Real may refer to:
Currencies
* Brazilian real (R$)
* Central American Republic real
* Mexican real
* Portuguese real
* Spanish real
* Spanish colonial real
Music Albums
* ''Real'' (L'Arc-en-Ciel album) (2000)
* ''Real'' (Bright album) (2010) ...
input , and outputs a value between zero and one. For the logit, this is interpreted as taking input log-odds and having output probability
Probability is the branch of mathematics concerning numerical descriptions of how likely an event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speakin ...
. The ''standard'' logistic function is defined as follows:
:
A graph of the logistic function on the ''t''-interval (−6,6) is shown in Figure 1.
Let us assume that is a linear function of a single explanatory variable (the case where is a ''linear combination'' of multiple explanatory variables is treated similarly). We can then express as follows:
:
And the general logistic function can now be written as:
:
In the logistic model, is interpreted as the probability of the dependent variable equaling a success/case rather than a failure/non-case. It's clear that the response variables are not identically distributed: differs from one data point to another, though they are independent given design matrix
In statistics and in particular in regression analysis, a design matrix, also known as model matrix or regressor matrix and often denoted by X, is a matrix of values of explanatory variables of a set of objects. Each row represents an individual ob ...
and shared parameters .
Definition of the inverse of the logistic function
We can now define thelogit
In statistics, the logit ( ) function is the quantile function associated with the standard logistic distribution. It has many uses in data analysis and machine learning, especially in data transformations.
Mathematically, the logit is the ...
(log odds) function as the inverse of the standard logistic function. It is easy to see that it satisfies:
:
and equivalently, after exponentiating both sides we have the odds:
:
Interpretation of these terms
In the above equations, the terms are as follows: * is the logit function. The equation for illustrates that thelogit
In statistics, the logit ( ) function is the quantile function associated with the standard logistic distribution. It has many uses in data analysis and machine learning, especially in data transformations.
Mathematically, the logit is the ...
(i.e., log-odds or natural logarithm of the odds) is equivalent to the linear regression expression.
* denotes the natural logarithm.
* is the probability that the dependent variable equals a case, given some linear combination of the predictors. The formula for illustrates that the probability of the dependent variable equaling a case is equal to the value of the logistic function of the linear regression expression. This is important in that it shows that the value of the linear regression expression can vary from negative to positive infinity and yet, after transformation, the resulting expression for the probability ranges between 0 and 1.
* is the intercept from the linear regression equation (the value of the criterion when the predictor is equal to zero).
* is the regression coefficient multiplied by some value of the predictor.
* base denotes the exponential function.
Definition of the odds
The odds of the dependent variable equaling a case (given some linear combination of the predictors) is equivalent to the exponential function of the linear regression expression. This illustrates how thelogit
In statistics, the logit ( ) function is the quantile function associated with the standard logistic distribution. It has many uses in data analysis and machine learning, especially in data transformations.
Mathematically, the logit is the ...
serves as a link function between the probability and the linear regression expression. Given that the logit ranges between negative and positive infinity, it provides an adequate criterion upon which to conduct linear regression and the logit is easily converted back into the odds.
So we define odds of the dependent variable equaling a case (given some linear combination of the predictors) as follows:
:
The odds ratio
For a continuous independent variable the odds ratio can be defined as: : This exponential relationship provides an interpretation for : The odds multiply by for every 1-unit increase in x.
For a binary independent variable the odds ratio is defined as where ''a'', ''b'', ''c'' and ''d'' are cells in a 2×2 contingency table.
This exponential relationship provides an interpretation for : The odds multiply by for every 1-unit increase in x.
For a binary independent variable the odds ratio is defined as where ''a'', ''b'', ''c'' and ''d'' are cells in a 2×2 contingency table.
Multiple explanatory variables
If there are multiple explanatory variables, the above expression can be revised to . Then when this is used in the equation relating the log odds of a success to the values of the predictors, the linear regression will be amultiple regression
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one ...
with ''m'' explanators; the parameters for all are all estimated.
Again, the more traditional equations are:
:
and
:
where usually .
Definition
The basic setup of logistic regression is as follows. We are given a dataset containing ''N'' points. Each point ''i'' consists of a set of ''m'' input variables ''x''1,''i'' ... ''x''''m,i'' (also called independent variables, explanatory variables, predictor variables, features, or attributes), and abinary
Binary may refer to:
Science and technology Mathematics
* Binary number, a representation of numbers using only two digits (0 and 1)
* Binary function, a function that takes two arguments
* Binary operation, a mathematical operation that ta ...
outcome variable ''Y''''i'' (also known as a dependent variable, response variable, output variable, or class), i.e. it can assume only the two possible values 0 (often meaning "no" or "failure") or 1 (often meaning "yes" or "success"). The goal of logistic regression is to use the dataset to create a predictive model of the outcome variable.
As in linear regression, the outcome variables ''Y''''i'' are assumed to depend on the explanatory variables ''x''1,''i'' ... ''x''''m,i''.
; Explanatory variables
The explanatory variables may be of any type: real-valued
In mathematics, value may refer to several, strongly related notions.
In general, a mathematical value may be any definite mathematical object. In elementary mathematics, this is most often a number – for example, a real number such as or an i ...
, binary
Binary may refer to:
Science and technology Mathematics
* Binary number, a representation of numbers using only two digits (0 and 1)
* Binary function, a function that takes two arguments
* Binary operation, a mathematical operation that ta ...
, categorical, etc. The main distinction is between continuous variables and discrete variables.
(Discrete variables referring to more than two possible choices are typically coded using dummy variables (or indicator variable
In regression analysis, a dummy variable (also known as indicator variable or just dummy) is one that takes the values 0 or 1 to indicate the absence or presence of some categorical effect that may be expected to shift the outcome. For example, i ...
s), that is, separate explanatory variables taking the value 0 or 1 are created for each possible value of the discrete variable, with a 1 meaning "variable does have the given value" and a 0 meaning "variable does not have that value".)
;Outcome variables
Formally, the outcomes ''Y''''i'' are described as being Bernoulli-distributed data, where each outcome is determined by an unobserved probability ''p''''i'' that is specific to the outcome at hand, but related to the explanatory variables. This can be expressed in any of the following equivalent forms:
::
The meanings of these four lines are:
# The first line expresses the probability distribution of each ''Y''''i'' : conditioned on the explanatory variables, it follows a Bernoulli distribution
In probability theory and statistics, the Bernoulli distribution, named after Swiss mathematician Jacob Bernoulli,James Victor Uspensky: ''Introduction to Mathematical Probability'', McGraw-Hill, New York 1937, page 45 is the discrete probabi ...
with parameters ''p''''i'', the probability of the outcome of 1 for trial ''i''. As noted above, each separate trial has its own probability of success, just as each trial has its own explanatory variables. The probability of success ''p''''i'' is not observed, only the outcome of an individual Bernoulli trial using that probability.
# The second line expresses the fact that the expected value of each ''Y''''i'' is equal to the probability of success ''p''''i'', which is a general property of the Bernoulli distribution. In other words, if we run a large number of Bernoulli trials using the same probability of success ''p''''i'', then take the average of all the 1 and 0 outcomes, then the result would be close to ''p''''i''. This is because doing an average this way simply computes the proportion of successes seen, which we expect to converge to the underlying probability of success.
# The third line writes out the probability mass function of the Bernoulli distribution, specifying the probability of seeing each of the two possible outcomes.
# The fourth line is another way of writing the probability mass function, which avoids having to write separate cases and is more convenient for certain types of calculations. This relies on the fact that ''Y''''i'' can take only the value 0 or 1. In each case, one of the exponents will be 1, "choosing" the value under it, while the other is 0, "canceling out" the value under it. Hence, the outcome is either ''p''''i'' or 1 − ''p''''i'', as in the previous line.
; Linear predictor function
The basic idea of logistic regression is to use the mechanism already developed for linear regression by modeling the probability ''p''''i'' using a linear predictor function In statistics and in machine learning, a linear predictor function is a linear function ( linear combination) of a set of coefficients and explanatory variables (independent variables), whose value is used to predict the outcome of a dependent vari ...
, i.e. a linear combination of the explanatory variables and a set of regression coefficient
In statistics, linear regression is a linear approach for modelling the relationship between a scalar response and one or more explanatory variables (also known as dependent and independent variables). The case of one explanatory variable is cal ...
s that are specific to the model at hand but the same for all trials. The linear predictor function for a particular data point ''i'' is written as:
:
where are regression coefficient
In statistics, linear regression is a linear approach for modelling the relationship between a scalar response and one or more explanatory variables (also known as dependent and independent variables). The case of one explanatory variable is cal ...
s indicating the relative effect of a particular explanatory variable on the outcome.
The model is usually put into a more compact form as follows:
* The regression coefficients ''β''0, ''β''1, ..., ''β''''m'' are grouped into a single vector ''β'' of size ''m'' + 1.
* For each data point ''i'', an additional explanatory pseudo-variable ''x''0,''i'' is added, with a fixed value of 1, corresponding to the intercept coefficient ''β''0.
* The resulting explanatory variables ''x''0,''i'', ''x''1,''i'', ..., ''x''''m,i'' are then grouped into a single vector ''Xi'' of size ''m'' + 1.
This makes it possible to write the linear predictor function as follows:
:
using the notation for a dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an alge ...
between two vectors.
Many explanatory variables, two categories
The above example of binary logistic regression on one explanatory variable can be generalized to binary logistic regression on any number of explanatory variables ''x1, x2,...'' and any number of categorical values . To begin with, we may consider a logistic model with ''M'' explanatory variables, ''x1'', ''x2'' ... ''xM'' and, as in the example above, two categorical values (''y'' = 0 and 1). For the simple binary logistic regression model, we assumed a linear relationship between the predictor variable and the log-odds (also calledlogit
In statistics, the logit ( ) function is the quantile function associated with the standard logistic distribution. It has many uses in data analysis and machine learning, especially in data transformations.
Mathematically, the logit is the ...
) of the event that . This linear relationship may be extended to the case of ''M'' explanatory variables:
:
where ''t'' is the log-odds and are parameters of the model. An additional generalization has been introduced in which the base of the model (''b'') is not restricted to the Euler number
In mathematics, the Euler numbers are a sequence ''En'' of integers defined by the Taylor series expansion
:\frac = \frac = \sum_^\infty \frac \cdot t^n,
where \cosh (t) is the hyperbolic cosine function. The Euler numbers are related to a ...
''e''. In most applications, the base of the logarithm is usually taken to be '' e''. However, in some cases it can be easier to communicate results by working in base 2 or base 10.
For a more compact notation, we will specify the explanatory variables and the ''β'' coefficients as -dimensional vectors:
:
:
with an added explanatory variable ''x0'' =1. The logit may now be written as:
:
Solving for the probability ''p'' that yields:
:,
where is the sigmoid function
A sigmoid function is a mathematical function having a characteristic "S"-shaped curve or sigmoid curve.
A common example of a sigmoid function is the logistic function shown in the first figure and defined by the formula:
:S(x) = \frac = \ ...
with base . The above formula shows that once the are fixed, we can easily compute either the log-odds that for a given observation, or the probability that for a given observation. The main use-case of a logistic model is to be given an observation x, and estimate the probability ''p(x)'' that . The optimum beta coefficients may again be found by maximizing the log-likelihood. For ''K'' measurements, defining xk as the explanatory vector of the ''k''-th measurement, and ''y''k as the categorical outcome of that measurement, the log likelihood may be written in a form very similar to the simple case above:
:
As in the simple example above, finding the optimum ''β'' parameters will require numerical methods. One useful technique is to equate the derivatives of the log likelihood with respect to each of the ''β'' parameters to zero yielding a set of equations which will hold at the maximum of the log likelihood:
:
where ''xmk'' is the value of the ''xm'' explanatory variable from the ''k-th'' measurement.
Consider an example with explanatory variables, , and coefficients , , and which have been determined by the above method. To be concrete, the model is:
:
:,
where ''p'' is the probability of the event that . This can be interpreted as follows:
* is the ''y''-intercept. It is the log-odds of the event that , when the predictors . By exponentiating, we can see that when the odds of the event that are 1-to-1000, or . Similarly, the probability of the event that when can be computed as
* means that increasing by 1 increases the log-odds by . So if increases by 1, the odds that increase by a factor of . Note that the probability of has also increased, but it has not increased by as much as the odds have increased.
* means that increasing by 1 increases the log-odds by . So if increases by 1, the odds that increase by a factor of Note how the effect of on the log-odds is twice as great as the effect of , but the effect on the odds is 10 times greater. But the effect on the probability of is not as much as 10 times greater, it's only the effect on the odds that is 10 times greater.
Multinomial logistic regression: Many explanatory variables and many categories
In the above cases of two categories (binomial logistic regression), the categories were indexed by "0" and "1", and we had two probability distributions: The probability that the outcome was in category 1 was given by and the probability that the outcome was in category 0 was given by . The sum of both probabilities is equal to unity, as they must be. In general, if we have explanatory variables (including ''x0'') and categories, we will need separate probability distributions, one for each category, indexed by ''n'', which describe the probability that the categorical outcome ''y'' for explanatory vector x will be in category ''y=n''. It will also be required that the sum of these probabilities over all categories be equal to unity. Using the mathematically convenient base ''e'', these probabilities are: : for : Each of the probabilities except will have their own set of regression coefficients . It can be seen that, as required, the sum of the over all categories is unity. Note that the selection of to be defined in terms of the other probabilities is artificial. Any of the probabilities could have been selected to be so defined. This special value of ''n'' is termed the "pivot index", and the log-odds (''tn'') are expressed in terms of the pivot probability and are again expressed as a linear combination of the explanatory variables: : Note also that for the simple case of , the two-category case is recovered, with and . The log-likelihood that a particular set of ''K'' measurements or data points will be generated by the above probabilities can now be calculated. Indexing each measurement by ''k'', let the ''k''-th set of measured explanatory variables be denoted by and their categorical outcomes be denoted by which can be equal to any integer in ,N The log-likelihood is then: : where is an indicator function which is equal to unity if ''yk = n'' and zero otherwise. In the case of two explanatory variables, this indicator function was defined as ''yk'' when ''n'' = 1 and ''1-yk'' when ''n'' = 0. This was convenient, but not necessary. Again, the optimum beta coefficients may be found by maximizing the log-likelihood function generally using numerical methods. A possible method of solution is to set the derivatives of the log-likelihood with respect to each beta coefficient equal to zero and solve for the beta coefficients: : where is the ''m''-th coefficient of the vector and is the ''m''-th explanatory variable of the ''k''-th measurement. Once the beta coefficients have been estimated from the data, we will be able to estimate the probability that any subsequent set of explanatory variables will result in any of the possible outcome categories.Interpretations
There are various equivalent specifications and interpretations of logistic regression, which fit into different types of more general models, and allow different generalizations.As a generalized linear model
The particular model used by logistic regression, which distinguishes it from standard linear regression and from other types ofregression analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one ...
used for binary-valued outcomes, is the way the probability of a particular outcome is linked to the linear predictor function:
:
Written using the more compact notation described above, this is:
:
This formulation expresses logistic regression as a type of generalized linear model, which predicts variables with various types of probability distributions by fitting a linear predictor function of the above form to some sort of arbitrary transformation of the expected value of the variable.
The intuition for transforming using the logit function (the natural log of the odds) was explained above. It also has the practical effect of converting the probability (which is bounded to be between 0 and 1) to a variable that ranges over — thereby matching the potential range of the linear prediction function on the right side of the equation.
Note that both the probabilities ''p''''i'' and the regression coefficients are unobserved, and the means of determining them is not part of the model itself. They are typically determined by some sort of optimization procedure, e.g. maximum likelihood estimation
In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of an assumed probability distribution, given some observed data. This is achieved by maximizing a likelihood function so that, under the assumed stati ...
, that finds values that best fit the observed data (i.e. that give the most accurate predictions for the data already observed), usually subject to regularization conditions that seek to exclude unlikely values, e.g. extremely large values for any of the regression coefficients. The use of a regularization condition is equivalent to doing maximum a posteriori
In Bayesian statistics, a maximum a posteriori probability (MAP) estimate is an estimate of an unknown quantity, that equals the mode of the posterior distribution. The MAP can be used to obtain a point estimate of an unobserved quantity on the ...
(MAP) estimation, an extension of maximum likelihood. (Regularization is most commonly done using a squared regularizing function, which is equivalent to placing a zero-mean Gaussian prior distribution on the coefficients, but other regularizers are also possible.) Whether or not regularization is used, it is usually not possible to find a closed-form solution; instead, an iterative numerical method must be used, such as iteratively reweighted least squares (IRLS) or, more commonly these days, a quasi-Newton method such as the L-BFGS method.
The interpretation of the ''β''''j'' parameter estimates is as the additive effect on the log of the odds
Odds provide a measure of the likelihood of a particular outcome. They are calculated as the ratio of the number of events that produce that outcome to the number that do not. Odds are commonly used in gambling and statistics.
Odds also have ...
for a unit change in the ''j'' the explanatory variable. In the case of a dichotomous explanatory variable, for instance, gender is the estimate of the odds of having the outcome for, say, males compared with females.
An equivalent formula uses the inverse of the logit function, which is the logistic function, i.e.:
:
The formula can also be written as a probability distribution (specifically, using a probability mass function):
:
As a latent-variable model
The logistic model has an equivalent formulation as a latent-variable model. This formulation is common in the theory of discrete choice models and makes it easier to extend to certain more complicated models with multiple, correlated choices, as well as to compare logistic regression to the closely relatedprobit model
In statistics, a probit model is a type of regression where the dependent variable can take only two values, for example married or not married. The word is a portmanteau, coming from ''probability'' + ''unit''. The purpose of the model is to est ...
.
Imagine that, for each trial ''i'', there is a continuous latent variable
In statistics, latent variables (from Latin: present participle of ''lateo'', “lie hidden”) are variables that can only be inferred indirectly through a mathematical model from other observable variables that can be directly observed or me ...
''Y''''i''* (i.e. an unobserved random variable) that is distributed as follows:
:
where
:
i.e. the latent variable can be written directly in terms of the linear predictor function and an additive random error variable that is distributed according to a standard logistic distribution
Logistic may refer to:
Mathematics
* Logistic function, a sigmoid function used in many fields
** Logistic map, a recurrence relation that sometimes exhibits chaos
** Logistic regression, a statistical model using the logistic function
** Logit, ...
.
Then ''Y''''i'' can be viewed as an indicator for whether this latent variable is positive:
:
The choice of modeling the error variable specifically with a standard logistic distribution, rather than a general logistic distribution with the location and scale set to arbitrary values, seems restrictive, but in fact, it is not. It must be kept in mind that we can choose the regression coefficients ourselves, and very often can use them to offset changes in the parameters of the error variable's distribution. For example, a logistic error-variable distribution with a non-zero location parameter ''μ'' (which sets the mean) is equivalent to a distribution with a zero location parameter, where ''μ'' has been added to the intercept coefficient. Both situations produce the same value for ''Y''''i''* regardless of settings of explanatory variables. Similarly, an arbitrary scale parameter ''s'' is equivalent to setting the scale parameter to 1 and then dividing all regression coefficients by ''s''. In the latter case, the resulting value of ''Y''''i''''*'' will be smaller by a factor of ''s'' than in the former case, for all sets of explanatory variables — but critically, it will always remain on the same side of 0, and hence lead to the same ''Y''''i'' choice.
(Note that this predicts that the irrelevancy of the scale parameter may not carry over into more complex models where more than two choices are available.)
It turns out that this formulation is exactly equivalent to the preceding one, phrased in terms of the generalized linear model and without any latent variable
In statistics, latent variables (from Latin: present participle of ''lateo'', “lie hidden”) are variables that can only be inferred indirectly through a mathematical model from other observable variables that can be directly observed or me ...
s. This can be shown as follows, using the fact that the cumulative distribution function (CDF) of the standard logistic distribution
Logistic may refer to:
Mathematics
* Logistic function, a sigmoid function used in many fields
** Logistic map, a recurrence relation that sometimes exhibits chaos
** Logistic regression, a statistical model using the logistic function
** Logit, ...
is the logistic function, which is the inverse of the logit function
In statistics, the logit ( ) function is the quantile function associated with the standard logistic distribution. It has many uses in data analysis and machine learning, especially in data transformations.
Mathematically, the logit is the in ...
, i.e.
:
Then:
:
This formulation—which is standard in discrete choice models—makes clear the relationship between logistic regression (the "logit model") and the probit model
In statistics, a probit model is a type of regression where the dependent variable can take only two values, for example married or not married. The word is a portmanteau, coming from ''probability'' + ''unit''. The purpose of the model is to est ...
, which uses an error variable distributed according to a standard normal distribution instead of a standard logistic distribution. Both the logistic and normal distributions are symmetric with a basic unimodal, "bell curve" shape. The only difference is that the logistic distribution has somewhat heavier tails, which means that it is less sensitive to outlying data (and hence somewhat more robust
Robustness is the property of being strong and healthy in constitution. When it is transposed into a system, it refers to the ability of tolerating perturbations that might affect the system’s functional body. In the same line ''robustness'' ca ...
to model mis-specifications or erroneous data).
Two-way latent-variable model
Yet another formulation uses two separate latent variables: : where : where ''EV''1(0,1) is a standard type-1extreme value distribution
In probability theory and statistics, the generalized extreme value (GEV) distribution is a family of continuous probability distributions developed within extreme value theory to combine the Gumbel, Fréchet and Weibull families also known ...
: i.e.
:
Then
:
This model has a separate latent variable and a separate set of regression coefficients for each possible outcome of the dependent variable. The reason for this separation is that it makes it easy to extend logistic regression to multi-outcome categorical variables, as in the multinomial logit
In statistics, multinomial logistic regression is a classification method that generalizes logistic regression to multiclass problems, i.e. with more than two possible discrete outcomes. That is, it is a model that is used to predict the prob ...
model. In such a model, it is natural to model each possible outcome using a different set of regression coefficients. It is also possible to motivate each of the separate latent variables as the theoretical utility
As a topic of economics, utility is used to model worth or value. Its usage has evolved significantly over time. The term was introduced initially as a measure of pleasure or happiness as part of the theory of utilitarianism by moral philosoph ...
associated with making the associated choice, and thus motivate logistic regression in terms of utility theory
As a topic of economics, utility is used to model worth or value. Its usage has evolved significantly over time. The term was introduced initially as a measure of pleasure or happiness as part of the theory of utilitarianism by moral philosopher ...
. (In terms of utility theory, a rational actor always chooses the choice with the greatest associated utility.) This is the approach taken by economists when formulating discrete choice models, because it both provides a theoretically strong foundation and facilitates intuitions about the model, which in turn makes it easy to consider various sorts of extensions. (See the example below.)
The choice of the type-1 extreme value distribution
In probability theory and statistics, the generalized extreme value (GEV) distribution is a family of continuous probability distributions developed within extreme value theory to combine the Gumbel, Fréchet and Weibull families also known ...
seems fairly arbitrary, but it makes the mathematics work out, and it may be possible to justify its use through rational choice theory.
It turns out that this model is equivalent to the previous model, although this seems non-obvious, since there are now two sets of regression coefficients and error variables, and the error variables have a different distribution. In fact, this model reduces directly to the previous one with the following substitutions:
:
:
An intuition for this comes from the fact that, since we choose based on the maximum of two values, only their difference matters, not the exact values — and this effectively removes one degree of freedom
Degrees of freedom (often abbreviated df or DOF) refers to the number of independent variables or parameters of a thermodynamic system. In various scientific fields, the word "freedom" is used to describe the limits to which physical movement or ...
. Another critical fact is that the difference of two type-1 extreme-value-distributed variables is a logistic distribution, i.e. We can demonstrate the equivalent as follows:
:
Example
: As an example, consider a province-level election where the choice is between a right-of-center party, a left-of-center party, and a secessionist party (e.g. theParti Québécois
The Parti Québécois (; ; PQ) is a sovereignist and social democratic provincial political party in Quebec, Canada. The PQ advocates national sovereignty for Quebec involving independence of the province of Quebec from Canada and establishin ...
, which wants Quebec
Quebec ( ; )According to the Canadian government, ''Québec'' (with the acute accent) is the official name in Canadian French and ''Quebec'' (without the accent) is the province's official name in Canadian English is one of the thirtee ...
to secede from Canada
Canada is a country in North America. Its ten provinces and three territories extend from the Atlantic Ocean to the Pacific Ocean and northward into the Arctic Ocean, covering over , making it the world's second-largest country by tot ...
). We would then use three latent variables, one for each choice. Then, in accordance with utility theory
As a topic of economics, utility is used to model worth or value. Its usage has evolved significantly over time. The term was introduced initially as a measure of pleasure or happiness as part of the theory of utilitarianism by moral philosopher ...
, we can then interpret the latent variables as expressing the utility
As a topic of economics, utility is used to model worth or value. Its usage has evolved significantly over time. The term was introduced initially as a measure of pleasure or happiness as part of the theory of utilitarianism by moral philosoph ...
that results from making each of the choices. We can also interpret the regression coefficients as indicating the strength that the associated factor (i.e. explanatory variable) has in contributing to the utility — or more correctly, the amount by which a unit change in an explanatory variable changes the utility of a given choice. A voter might expect that the right-of-center party would lower taxes, especially on rich people. This would give low-income people no benefit, i.e. no change in utility (since they usually don't pay taxes); would cause moderate benefit (i.e. somewhat more money, or moderate utility increase) for middle-incoming people; would cause significant benefits for high-income people. On the other hand, the left-of-center party might be expected to raise taxes and offset it with increased welfare and other assistance for the lower and middle classes. This would cause significant positive benefit to low-income people, perhaps a weak benefit to middle-income people, and significant negative benefit to high-income people. Finally, the secessionist party would take no direct actions on the economy, but simply secede. A low-income or middle-income voter might expect basically no clear utility gain or loss from this, but a high-income voter might expect negative utility since he/she is likely to own companies, which will have a harder time doing business in such an environment and probably lose money.
These intuitions can be expressed as follows:
This clearly shows that
# Separate sets of regression coefficients need to exist for each choice. When phrased in terms of utility, this can be seen very easily. Different choices have different effects on net utility; furthermore, the effects vary in complex ways that depend on the characteristics of each individual, so there need to be separate sets of coefficients for each characteristic, not simply a single extra per-choice characteristic.
# Even though income is a continuous variable, its effect on utility is too complex for it to be treated as a single variable. Either it needs to be directly split up into ranges, or higher powers of income need to be added so that polynomial regression
In statistics, polynomial regression is a form of regression analysis in which the relationship between the independent variable ''x'' and the dependent variable ''y'' is modelled as an ''n''th degree polynomial in ''x''. Polynomial regression fi ...
on income is effectively done.
As a "log-linear" model
Yet another formulation combines the two-way latent variable formulation above with the original formulation higher up without latent variables, and in the process provides a link to one of the standard formulations of themultinomial logit
In statistics, multinomial logistic regression is a classification method that generalizes logistic regression to multiclass problems, i.e. with more than two possible discrete outcomes. That is, it is a model that is used to predict the prob ...
.
Here, instead of writing the logit
In statistics, the logit ( ) function is the quantile function associated with the standard logistic distribution. It has many uses in data analysis and machine learning, especially in data transformations.
Mathematically, the logit is the ...
of the probabilities ''p''''i'' as a linear predictor, we separate the linear predictor into two, one for each of the two outcomes:
:
Two separate sets of regression coefficients have been introduced, just as in the two-way latent variable model, and the two equations appear a form that writes the logarithm
In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a number to the base is the exponent to which must be raised, to produce . For example, since , the ''logarithm base'' 10 of ...
of the associated probability as a linear predictor, with an extra term at the end. This term, as it turns out, serves as the normalizing factor ensuring that the result is a distribution. This can be seen by exponentiating both sides:
:
In this form it is clear that the purpose of ''Z'' is to ensure that the resulting distribution over ''Y''''i'' is in fact a probability distribution, i.e. it sums to 1. This means that ''Z'' is simply the sum of all un-normalized probabilities, and by dividing each probability by ''Z'', the probabilities become " normalized". That is:
:
and the resulting equations are
:
Or generally:
:
This shows clearly how to generalize this formulation to more than two outcomes, as in multinomial logit
In statistics, multinomial logistic regression is a classification method that generalizes logistic regression to multiclass problems, i.e. with more than two possible discrete outcomes. That is, it is a model that is used to predict the prob ...
.
Note that this general formulation is exactly the softmax function
The softmax function, also known as softargmax or normalized exponential function, converts a vector of real numbers into a probability distribution of possible outcomes. It is a generalization of the logistic function to multiple dimensions, a ...
as in
:
In order to prove that this is equivalent to the previous model, note that the above model is overspecified, in that and cannot be independently specified: rather so knowing one automatically determines the other. As a result, the model is nonidentifiable
In statistics, identifiability is a property which a model must satisfy for precise inference to be possible. A model is identifiable if it is theoretically possible to learn the true values of this model's underlying parameters after obtaining an ...
, in that multiple combinations of ''β''0 and ''β''1 will produce the same probabilities for all possible explanatory variables. In fact, it can be seen that adding any constant vector to both of them will produce the same probabilities:
:
As a result, we can simplify matters, and restore identifiability, by picking an arbitrary value for one of the two vectors. We choose to set Then,
:
and so
:
which shows that this formulation is indeed equivalent to the previous formulation. (As in the two-way latent variable formulation, any settings where will produce equivalent results.)
Note that most treatments of the multinomial logit
In statistics, multinomial logistic regression is a classification method that generalizes logistic regression to multiclass problems, i.e. with more than two possible discrete outcomes. That is, it is a model that is used to predict the prob ...
model start out either by extending the "log-linear" formulation presented here or the two-way latent variable formulation presented above, since both clearly show the way that the model could be extended to multi-way outcomes. In general, the presentation with latent variables is more common in econometrics
Econometrics is the application of statistical methods to economic data in order to give empirical content to economic relationships. M. Hashem Pesaran (1987). "Econometrics," '' The New Palgrave: A Dictionary of Economics'', v. 2, p. 8 p. 8 ...
and political science
Political science is the scientific study of politics. It is a social science dealing with systems of governance and power, and the analysis of political activities, political thought, political behavior, and associated constitutions and la ...
, where discrete choice models and utility theory
As a topic of economics, utility is used to model worth or value. Its usage has evolved significantly over time. The term was introduced initially as a measure of pleasure or happiness as part of the theory of utilitarianism by moral philosopher ...
reign, while the "log-linear" formulation here is more common in computer science
Computer science is the study of computation, automation, and information. Computer science spans theoretical disciplines (such as algorithms, theory of computation, information theory, and automation) to practical disciplines (includi ...
, e.g. machine learning
Machine learning (ML) is a field of inquiry devoted to understanding and building methods that 'learn', that is, methods that leverage data to improve performance on some set of tasks. It is seen as a part of artificial intelligence.
Machine ...
and natural language processing.
As a single-layer perceptron
The model has an equivalent formulation : This functional form is commonly called a single-layerperceptron
In machine learning, the perceptron (or McCulloch-Pitts neuron) is an algorithm for supervised learning of binary classifiers. A binary classifier is a function which can decide whether or not an input, represented by a vector of numbers, belon ...
or single-layer artificial neural network
Artificial neural networks (ANNs), usually simply called neural networks (NNs) or neural nets, are computing systems inspired by the biological neural networks that constitute animal brains.
An ANN is based on a collection of connected unit ...
. A single-layer neural network computes a continuous output instead of a step function
In mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of intervals. Informally speaking, a step function is a piecewise constant function having onl ...
. The derivative of ''pi'' with respect to ''X'' = (''x''1, ..., ''x''''k'') is computed from the general form:
:
where ''f''(''X'') is an analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions. Functions of each type are infinitely differentiable, but complex ...
in ''X''. With this choice, the single-layer neural network is identical to the logistic regression model. This function has a continuous derivative, which allows it to be used in backpropagation
In machine learning, backpropagation (backprop, BP) is a widely used algorithm for training feedforward artificial neural networks. Generalizations of backpropagation exist for other artificial neural networks (ANNs), and for functions gener ...
. This function is also preferred because its derivative is easily calculated:
:
In terms of binomial data
A closely related model assumes that each ''i'' is associated not with a single Bernoulli trial but with ''n''''i'' independent identically distributed trials, where the observation ''Y''''i'' is the number of successes observed (the sum of the individual Bernoulli-distributed random variables), and hence follows a binomial distribution: : An example of this distribution is the fraction of seeds (''p''''i'') that germinate after ''n''''i'' are planted. In terms of expected values, this model is expressed as follows: : so that : Or equivalently: : This model can be fit using the same sorts of methods as the above more basic model.Model fitting
Maximum likelihood estimation (MLE)
The regression coefficients are usually estimated usingmaximum likelihood estimation
In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of an assumed probability distribution, given some observed data. This is achieved by maximizing a likelihood function so that, under the assumed stati ...
. Unlike linear regression with normally distributed residuals, it is not possible to find a closed-form expression for the coefficient values that maximize the likelihood function, so that an iterative process must be used instead; for example Newton's method. This process begins with a tentative solution, revises it slightly to see if it can be improved, and repeats this revision until no more improvement is made, at which point the process is said to have converged.
In some instances, the model may not reach convergence. Non-convergence of a model indicates that the coefficients are not meaningful because the iterative process was unable to find appropriate solutions. A failure to converge may occur for a number of reasons: having a large ratio of predictors to cases, multicollinearity
In statistics, multicollinearity (also collinearity) is a phenomenon in which one predictor variable in a multiple regression model can be linearly predicted from the others with a substantial degree of accuracy. In this situation, the coeffic ...
, sparseness
Neural coding (or Neural representation) is a neuroscience field concerned with characterising the hypothetical relationship between the stimulus and the individual or ensemble neuronal responses and the relationship among the electrical activity ...
, or complete separation.
* Having a large ratio of variables to cases results in an overly conservative Wald statistic (discussed below) and can lead to non-convergence. Regularized logistic regression is specifically intended to be used in this situation.
* Multicollinearity refers to unacceptably high correlations between predictors. As multicollinearity increases, coefficients remain unbiased but standard errors increase and the likelihood of model convergence decreases. To detect multicollinearity amongst the predictors, one can conduct a linear regression analysis with the predictors of interest for the sole purpose of examining the tolerance statistic used to assess whether multicollinearity is unacceptably high.
* Sparseness in the data refers to having a large proportion of empty cells (cells with zero counts). Zero cell counts are particularly problematic with categorical predictors. With continuous predictors, the model can infer values for the zero cell counts, but this is not the case with categorical predictors. The model will not converge with zero cell counts for categorical predictors because the natural logarithm of zero is an undefined value so that the final solution to the model cannot be reached. To remedy this problem, researchers may collapse categories in a theoretically meaningful way or add a constant to all cells.
* Another numerical problem that may lead to a lack of convergence is complete separation, which refers to the instance in which the predictors perfectly predict the criterion – all cases are accurately classified and the likelihood maximized with infinite coefficients. In such instances, one should re-examine the data, as there may be some kind of error.
* One can also take semi-parametric or non-parametric approaches, e.g., via local-likelihood or nonparametric quasi-likelihood methods, which avoid assumptions of a parametric form for the index function and is robust to the choice of the link function (e.g., probit or logit).
Iteratively reweighted least squares (IRLS)
Binary logistic regression ( or ) can, for example, be calculated using ''iteratively reweighted least squares'' (IRLS), which is equivalent to maximizing thelog-likelihood
The likelihood function (often simply called the likelihood) represents the probability of random variable realizations conditional on particular values of the statistical parameters. Thus, when evaluated on a given sample, the likelihood functi ...
of a Bernoulli distributed process using Newton's method. If the problem is written in vector matrix form, with parameters