Lifting Property

In mathematics, in particular in category theory, the lifting property is a property of a pair of morphisms in a category. It is used in homotopy theory within algebraic topology to define properties of morphisms starting from an explicitly given class of morphisms. It appears in a prominent way in the theory of model categories, an axiomatic framework for homotopy theory introduced by Daniel Quillen. It is also used in the definition of a factorization system, and of a weak factorization system, notions related to but less restrictive than the notion of a model category. Several elementary notions may also be expressed using the lifting property starting from a list of (counter)examples.

Formal definition

A morphism $i$ in a category has the ''left lifting property'' with respect to a morphism $p$, and $p$ also has the ''right lifting property'' with respect to $i$, sometimes denoted $i\perp p$ or $i\downarrow p$, iff the following implication holds for each morphism $f$ and $g$ in the category:

* if the outer square of the following diagram commutes, then there exists $h$ completing the diagram, i.e. for each $f:A\to X$ and $g:B\to Y$ such that $p\circ f = g \circ i$ there exists $h:B\to X$ such that $h\circ i = f$ and $p\circ h = g$.

::

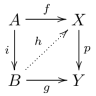
This is sometimes also known as the morphism $i$ being ''orthogonal to'' the morphism $p$; however, this can also refer to
the stronger property that whenever $f$ and $g$ are as above, the diagonal morphism $h$ exists and is also required to be unique.

For a class $C$ of morphisms in a category, its ''left orthogonal'' $C^$ or $C^\perp$ with respect to the lifting property, respectively its ''right orthogonal'' $C^$ or $^\perp C$, is the class of all morphisms which have the left, respectively right, lifting property with respect to each morphism in the class $C$. In notation,

:$\begin C^ &:= \ \\ C^ &:= \ \end$

Taking the orthogonal of a class $C$ is a simple way to define a class of morphisms excluding non-isomorphisms from $C$, in a way which is useful in a diagram chasing computation.

Thus, in the category Set of sets, the right orthogonal $\^$ of the simplest non-surjection $\emptyset\to \,$ is the class of surjections. The left and right orthogonals of $\\to \,$ the simplest non-injection, are both precisely the class of injections,

:$\^ = \^ = \.$

It is clear that $C^ \supset C$ and $C^ \supset C$. The class $C^$ is always closed under retracts, pullbacks, (small) products (whenever they exist in the category) & composition of morphisms, and contains all isomorphisms (that is, invertible morphisms) of the underlying category. Meanwhile, $C^$ is closed under retracts, pushouts, (small) coproducts & transfinite composition ( filtered colimits) of morphisms (whenever they exist in the category), and also contains all isomorphisms.

Examples

A number of notions can be defined by passing to the left or right orthogonal several times starting from a list of explicit examples, i.e. as $C^, C^, C^, C^$, where $C$ is a class consisting of several explicitly given morphisms. A useful intuition is to think that the property of left-lifting against a class $C$ is a kind of negation
of the property of being in $C$, and that right-lifting is also a kind of negation. Hence the classes obtained from $C$ by taking orthogonals an odd number of times, such as $C^, C^, C^, C^$ etc., represent various kinds of negation of $C$, so $C^, C^, C^, C^$ each consists of morphisms which are far from having property $C$.

Examples of lifting properties in algebraic topology

A map $f:U\to B$ has the ''path lifting property'' iff \\to ,1\perp f where \ \to ,1/math> is the inclusion of one end point of the closed interval into the interval ,1/math>.

A map $f:U\to B$ has the homotopy lifting property iff X \to X\times ,1\perp f where X\to X\times ,1/math> is the map $x \mapsto (x,0)$.

Examples of lifting properties coming from model categories

Fibrations and cofibrations.

* Let Top be the category of topological spaces, and let $C_0$ be the class of maps $S^n\to D^$, embeddings of the boundary $S^n=\partial D^$ of a ball into the ball $D^$. Let $WC_0$ be the class of maps embedding the upper semi-sphere into the disk. $WC_0^, WC_0^, C_0^, C_0^$ are the classes of fibrations, acyclic cofibrations, acyclic fibrations, and cofibrations.

* Let sSet be the category of simplicial sets. Let $C_0$ be the class of boundary inclusions \partial \Delta \to \Delta /math>, and let $WC_0$ be the class of horn inclusions \Lambda^i \to \Delta /math>. Then the classes of fibrations, acyclic cofibrations, acyclic fibrations, and cofibrations are, respectively, $WC_0^, WC_0^, C_0^, C_0^$.

* Let $\mathbf(R)$ be the category of chain complexes over a commutative ring $R$. Let $C_0$ be the class of maps of form
:: $\cdots\to 0\to R \to 0 \to 0 \to \cdots \to \cdots \to R \xrightarrow R \to 0 \to 0 \to \cdots,$
: and $WC_0$ be
:: $\cdots \to 0\to 0 \to 0 \to 0 \to \cdots \to \cdots \to R \xrightarrow R \to 0 \to 0 \to \cdots.$
:Then $WC_0^, WC_0^, C_0^, C_0^$ are the classes of fibrations, acyclic cofibrations, acyclic fibrations, and cofibrations. Def. 2.3.3, Th.2.3.11

Elementary examples in various categories

In Set,

* $\^$ is the class of surjections,

* $(\\to \)^=(\\to \)^$ is the class of injections.

In the category $R\text\mathbf$ of modules over a commutative ring $R$,

* $\^, \^$ is the class of surjections, resp. injections,

* A module $M$ is projective, resp. injective, iff $0\to M$ is in $\^$, resp. $M\to 0$ is in $\^$.

In the category $\mathbf$ of groups,

* $\^$, resp. $\^$, is the class of injections, resp. surjections (where $\Z$ denotes the infinite cyclic group),

* A group $F$ is a free group iff $0\to F$ is in $\^,$

* A group $A$ is torsion-free iff $0\to A$ is in $\^,$

* A subgroup $A$ of $B$ is pure iff $A \to B$ is in $\^.$

For a finite group $G$,

* $\ \perp 1\to G$ iff the order of $G$ is prime to $p$ iff $\ \perp G\to 1$,

* $G\to 1 \in (0\to /p)^$ iff $G$ is a $p$-group,

* $H$ is nilpotent iff the diagonal map $H\to H\times H$ is in $(1\to *)^$ where $(1\to *)$ denotes the class of maps $\,$

* a finite group $H$ is soluble iff $1\to H$ is in $\^=\^.$

In the category $\mathbf$ of topological spaces, let $\$, resp. $\$ denote the discrete, resp. antidiscrete space with two points 0 and 1. Let $\$ denote the Sierpinski space of two points where the point 0 is open and the point 1 is closed, and let $\\to \, \ \to \$ etc. denote the obvious embeddings.

* a space $X$ satisfies the separation axiom T₀ iff $X\to \$ is in $(\ \to \)^,$

* a space $X$ satisfies the separation axiom T₁ iff $\emptyset\to X$ is in $( \\to \)^,$

* $(\\to \)^$ is the class of maps with dense image,

* $(\\to \)^$ is the class of maps $f:X\to Y$ such that the topology on $A$ is the pullback of topology on $B$, i.e. the topology on $A$ is the topology with least number of open sets such that the map is continuous,

* $(\emptyset\to \)^$ is the class of surjective maps,

* $(\emptyset\to \)^$ is the class of maps of form $A\to A\cup D$ where $D$ is discrete,

* $(\emptyset\to \)^ = (\\to \)^$ is the class of maps $A\to B$ such that each connected component of $B$ intersects $\operatorname A$,

* $(\\to \)^$ is the class of injective maps,

* $(\\to \)^$ is the class of maps $f:X\to Y$ such that the preimage of a connected closed open subset of $Y$ is a connected closed open subset of $X$, e.g. $X$ is connected iff $X\to \$ is in $(\ \to \)^$,

* for a connected space $X$, each continuous function on $X$ is bounded iff $\emptyset\to X \perp \cup_n (-n,n) \to \R$ where $\cup_n (-n,n) \to \R$ is the map from the disjoint union of open intervals $(-n,n)$ into the real line $\mathbb,$

* a space $X$ is Hausdorff iff for any injective map $\\hookrightarrow X$, it holds $\\hookrightarrow X \perp \\to\$ where $\$ denotes the three-point space with two open points $a$ and $b$, and a closed point $x$,

* a space $X$ is perfectly normal iff \emptyset\to X \perp ,1\to \ where the open interval $(0,1)$ goes to $x$, and $0$ maps to the point $0$, and $1$ maps to the point $1$, and $\$ denotes the three-point space with two closed points $0, 1$ and one open point $x$.

In the category of metric spaces with uniformly continuous maps.

* A space $X$ is complete iff $\_ \to \\cup \_ \perp X\to \$ where $\_ \to \\cup \_$ is the obvious inclusion between the two subspaces of the real line with induced metric, and $\$ is the metric space consisting of a single point,

* A subspace $i:A\to X$ is closed iff $\_ \to \\cup \_ \perp A\to X.$

Notes

References

* {{cite book , last = Hovey , first = Mark , title = Model Categories , url = https://archive.org/details/arxiv-math9803002 , date=1999
* J. P. May and K. Ponto, More Concise Algebraic Topology: Localization, completion, and model categories

Category theory