spherical geometry 300px, A sphere with a spherical triangle on it. Spherical geometry or spherics () is the geometry of the two-dimensional surface of a sphere or the -dimensional surface of higher dimensional spheres. Long studied for its practical applicati ...

, Lexell's theorem holds that every

spherical triangle Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are gre ...

with the same

surface area The surface area (symbol ''A'') of a solid object is a measure of the total area that the surface of the object occupies. The mathematical definition of surface area in the presence of curved surfaces is considerably more involved than the d ...

on a fixed base has its

apex The apex is the highest point of something. The word may also refer to: Arts and media Fictional entities * Apex (comics) A-Bomb Abomination Absorbing Man Abraxas Abyss Abyss is the name of two characters appearing in Ameri ...

on a

small circle In spherical geometry, a spherical circle (often shortened to circle) is the locus of points on a sphere at constant spherical distance (the ''spherical radius'') from a given point on the sphere (the ''pole'' or ''spherical center''). It is ...

, called ''Lexell's circle'' or ''Lexell's

locus Locus (plural loci) is Latin for "place". It may refer to: Mathematics and science * Locus (mathematics), the set of points satisfying a particular condition, often forming a curve * Root locus analysis, a diagram visualizing the position of r ...

'', passing through each of the two points

antipodal Antipode or Antipodes may refer to: Mathematics * Antipodal point, the diametrically opposite point on a circle or ''n''-sphere, also known as an antipode * Antipode, the convolution inverse of the identity on a Hopf algebra Geography * Antipodes ...

to the two base vertices. A ''spherical triangle'' is a shape on a

sphere A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three ...

consisting of three vertices (corner points) connected by three sides, each of which is part of a ''

great circle In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point. Discussion Any arc of a great circle is a geodesic of the sphere, so that great circles in spher ...

'' (the analog on the sphere of a

straight line In geometry, a straight line, usually abbreviated line, is an infinitely long object with no width, depth, or curvature, an idealization of such physical objects as a straightedge, a taut string, or a ray of light. Lines are spaces of dimens ...

in the

plane Plane most often refers to: * Aero- or airplane, a powered, fixed-wing aircraft * Plane (geometry), a flat, 2-dimensional surface * Plane (mathematics), generalizations of a geometrical plane Plane or planes may also refer to: Biology * Plane ...

, for example the

equator The equator is the circle of latitude that divides Earth into the Northern Hemisphere, Northern and Southern Hemisphere, Southern Hemispheres of Earth, hemispheres. It is an imaginary line located at 0 degrees latitude, about in circumferen ...

and

meridian Meridian or a meridian line (from Latin ''meridies'' via Old French ''meridiane'', meaning “midday”) may refer to Science * Meridian (astronomy), imaginary circle in a plane perpendicular to the planes of the celestial equator and horizon * ...

s of a globe). Any of the sides of a spherical triangle can be considered the ''base'', and the opposite vertex is the corresponding ''apex''. Two points on a sphere are ''antipodal'' if they are diametrically opposite, as far apart as possible. The

theorem In mathematics and formal logic, a theorem is a statement (logic), statement that has been Mathematical proof, proven, or can be proven. The ''proof'' of a theorem is a logical argument that uses the inference rules of a deductive system to esta ...

is named for

Anders Johan Lexell Anders Johan Lexell (24 December 1740 – ) was a Finnish-Swedish astronomer, mathematician, and physicist who spent most of his life in Imperial Russia, where he was known as Andrei Ivanovich Leksel (Андрей Иванович Лексе ...

, who presented a paper about it (published 1784) including both a

trigonometric Trigonometry () is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle with ratios of its side lengths. The field ...

proof and a

geometric Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...

one. Lexell's colleague

Leonhard Euler Leonhard Euler ( ; ; ; 15 April 170718 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential ...

wrote another pair of proofs in 1778 (published 1797), and a variety of proofs have been written since by

Adrien-Marie Legendre Adrien-Marie Legendre (; ; 18 September 1752 – 9 January 1833) was a French people, French mathematician who made numerous contributions to mathematics. Well-known and important concepts such as the Legendre polynomials and Legendre transforma ...

(1800),

Jakob Steiner Jakob Steiner (18 March 1796 – 1 April 1863) was a Swiss mathematician who worked primarily in geometry. Life Steiner was born in the village of Utzenstorf, Canton of Bern. At 18, he became a pupil of Heinrich Pestalozzi and afterwards st ...

(1827),

Carl Friedrich Gauss Johann Carl Friedrich Gauss (; ; ; 30 April 177723 February 1855) was a German mathematician, astronomer, geodesist, and physicist, who contributed to many fields in mathematics and science. He was director of the Göttingen Observatory and ...

(1841),

Paul Serret Paul may refer to: People * Paul (given name), a given name, including a list of people * Paul (surname), a list of people * Paul the Apostle, an apostle who wrote many of the books of the New Testament * Ray Hildebrand, half of the singing duo P ...

(1855), and

Joseph-Émile Barbier Joseph-Émile Barbier (1839–1889) was a French astronomer and mathematician, known for Barbier's theorem on the perimeter of curves of constant width. Barbier was born on 18 March 1839 in Saint-Hilaire-Cottes, Pas-de-Calais, in the north of ...

(1864), among others. The theorem is the analog of propositions 37 and 39 in Book I of Euclid's ''Elements'', which prove that every planar triangle with the same area on a fixed base has its apex on a

parallel Parallel may refer to: Mathematics * Parallel (geometry), two lines in the Euclidean plane which never intersect * Parallel (operator), mathematical operation named after the composition of electrical resistance in parallel circuits Science a ...

to the base. An analogous theorem can also be proven for

hyperbolic triangle In hyperbolic geometry, a hyperbolic triangle is a triangle in the hyperbolic plane. It consists of three line segments called ''sides'' or ''edges'' and three point (geometry), points called ''angles'' or ''vertices''. Just as in the Euclidea ...

s, for which the apex lies on a hypercycle.

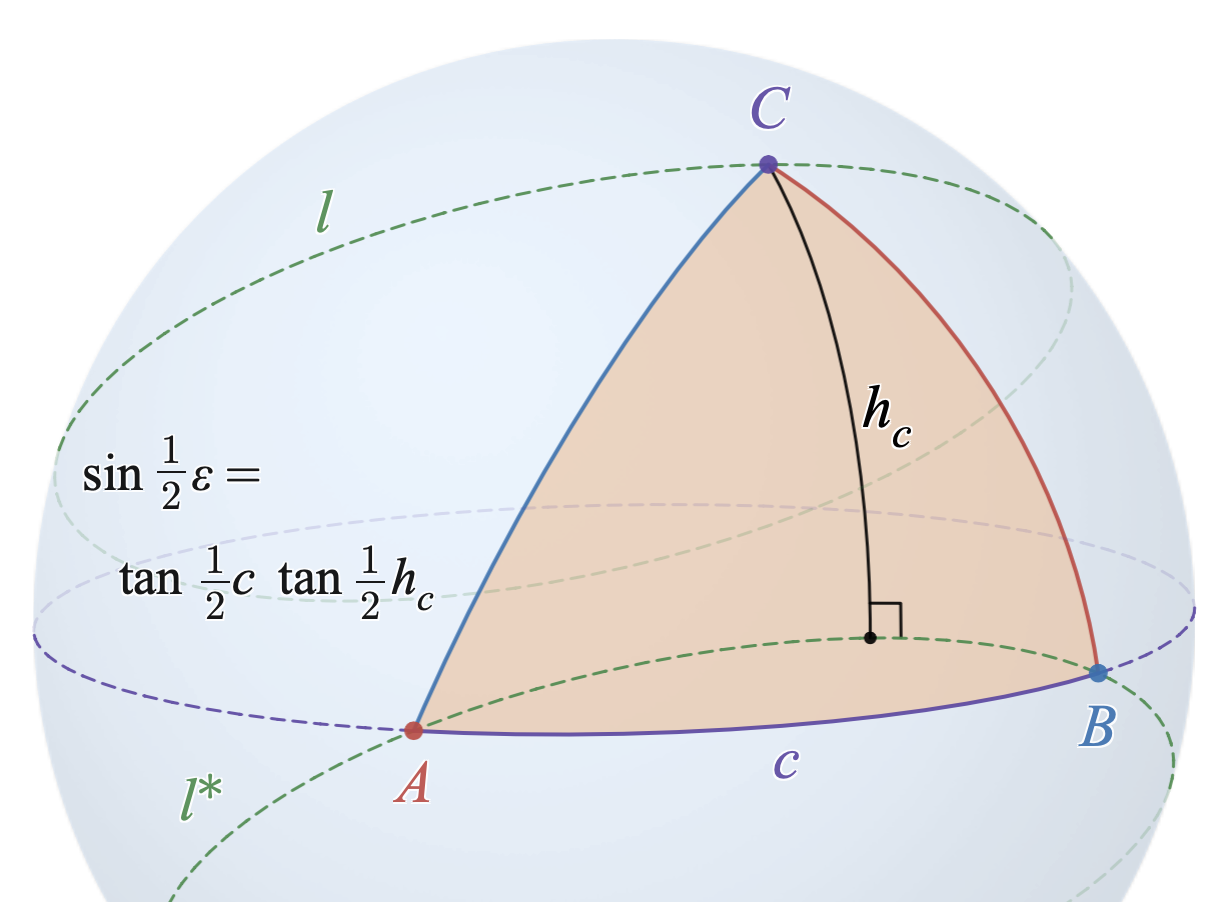
Statement

Area of a spherical triangle via Lexell circles

Given a fixed base

AB,

an arc of a

on a sphere, and two apex points

C

and

X

on the same side of great circle

AB,

Lexell's theorem holds that the surface area of the spherical triangle

\triangle ABX

is equal to that of

\triangle ABC

if and only if In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either bo ...

X

lies on the small-circle arc

B^* C A^*\!,

where

A^*

and

B^*

are the points antipodal to

A

and

B,

respectively. As one analog of the planar formula

\text = \tfrac12 \, \text \cdot \text

for the

area of a triangle In geometry, calculating the area of a triangle is an elementary problem encountered often in many different situations. The best known and simplest formula is T=bh/2, where ''b'' is the length of the ''base'' of the triangle, and ''h'' is the ' ...

, the

spherical excess Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are gre ...

\varepsilon

of spherical triangle

\triangle ABC

can be computed in terms of the base

c

(the angular length of arc and "height"

h_c

(the angular distance between the parallel small circles :

\sin \tfrac12 \varepsilon = \tan \tfrac12 c \, \tan\tfrac12 h_c.

This formula is based on consideration of a sphere of radius

1

, on which arc length is called ''

angle measure In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight lines at a point. Formally, an angle is a figure lying in a plane formed by two rays, called the '' sides'' of the angle, sharing ...

'' and surface area is called ''spherical excess'' or ''

solid angle In geometry, a solid angle (symbol: ) is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point. The poin ...

measure''. The angle measure of a complete great circle is

2\pi

radians The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at ...

, and the spherical excess of a hemisphere (half-sphere) is

2\pi

steradians The steradian (symbol: sr) or square radian is the unit of solid angle in the International System of Units (SI). It is used in three-dimensional geometry, and is analogous to the radian, which quantifies planar angles. A solid angle in the for ...

, where

\pi

is the circle constant. In the limit for triangles much smaller than the

radius In classical geometry, a radius (: radii or radiuses) of a circle or sphere is any of the line segments from its Centre (geometry), center to its perimeter, and in more modern usage, it is also their length. The radius of a regular polygon is th ...

of the sphere, this reduces to the planar formula. The small circles

A^* B^* C

and

A B C^*

each intersect the great circle

AB

at an angle of

\tfrac12 \varepsilon.

Proofs

There are several ways to prove Lexell's theorem, each illuminating a different aspect of the relationships involved.

Isosceles triangles

The main idea in Lexell's geometric proof – also adopted by

Eugène Catalan Eugene is a common male given name that comes from the Greek εὐγενής (''eugenēs''), "noble", literally "well-born", from εὖ (''eu''), "well" and γένος (''genos''), "race, stock, kin".Robert Allardice (1883),

Jacques Hadamard Jacques Salomon Hadamard (; 8 December 1865 – 17 October 1963) was a French mathematician who made major contributions in number theory, complex analysis, differential geometry, and partial differential equations. Biography The son of a tea ...

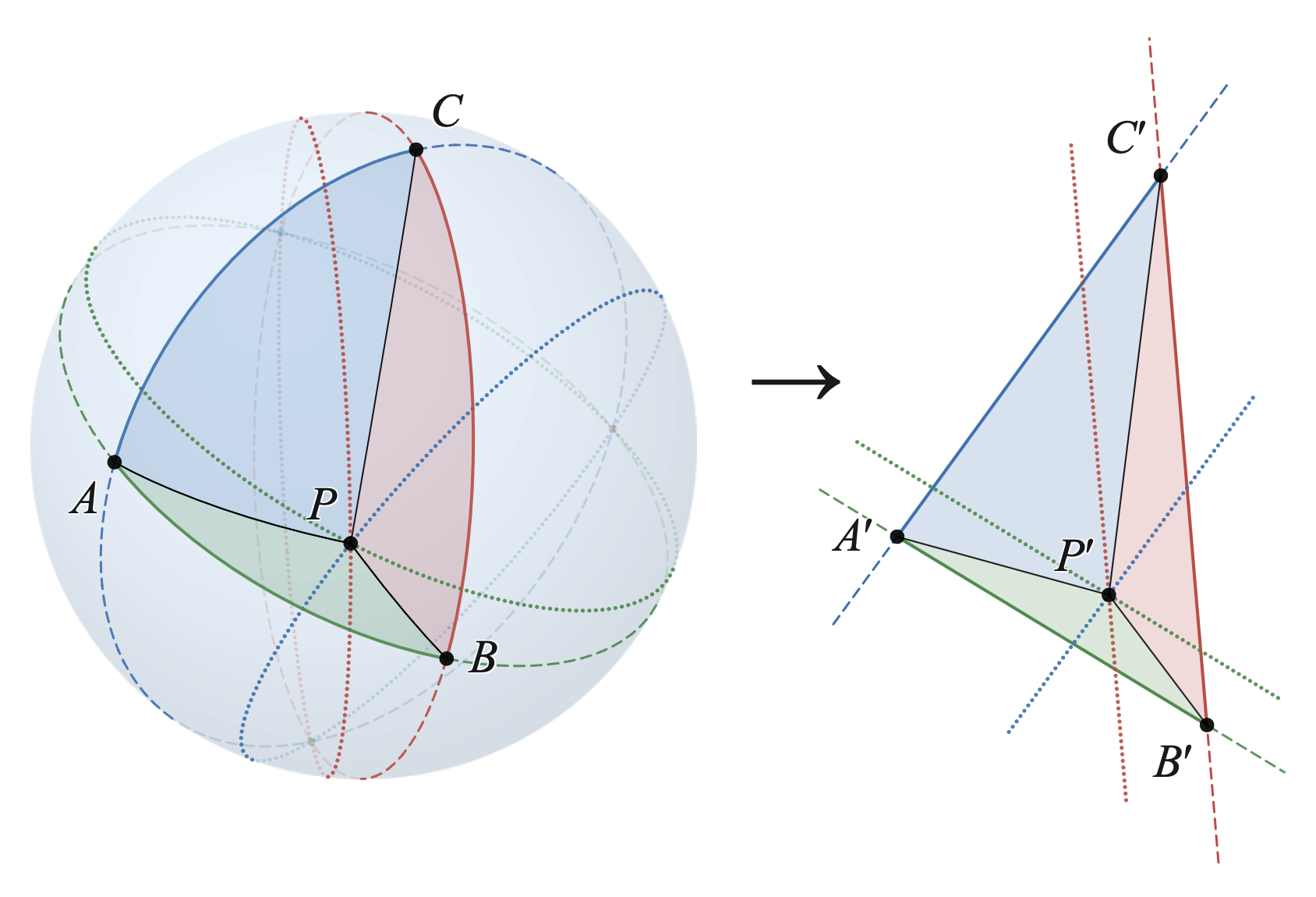
(1901), Antoine Gob (1922), and Hiroshi Maehara (1999) – is to split the triangle

\triangle A^* B^* C

into three isosceles triangles with common apex at the

circumcenter In geometry, the circumscribed circle or circumcircle of a triangle is a circle that passes through all three vertices. The center of this circle is called the circumcenter of the triangle, and its radius is called the circumradius. The circumcen ...

P

and then chase angles to find the spherical excess

\varepsilon

of triangle

\triangle ABC.

In the figure, points

A

and

B

are on the far side of the sphere so that we can clearly see their antipodal points and all of Lexell's circle

l.

Let the base angles of the isosceles triangles

\triangle B^* C P

(shaded red in the figure),

\triangle CA^* P

(blue), and

\triangle A^* B^* P

(purple) be respectively

\alpha,

\beta,

and

\delta.

(In some cases

P

is outside then one of the quantities

\alpha, \beta, \delta

will be negative.) We can compute the internal angles of

\triangle ABC

(orange) in terms of these angles:

\angle A = \pi - \beta - \delta

(the supplement of and likewise

\angle B = \pi - \alpha - \delta,

and finally

\angle C = \alpha + \beta.

Girard's theorem Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are grea ...

the spherical excess of

\triangle ABC

is :

&= \pi - 2\delta. \end

If base

AB

is fixed, for any third vertex

C

falling on the same arc of Lexell's circle, the point

P

and therefore the quantity

\delta

will not change, so the excess

\varepsilon

\triangle ABC,

which depends only on

\delta,

will likewise be constant. And vice versa: if

\varepsilon

remains constant when the point

C

is changed, then so must

\delta

be, and therefore

P

must be fixed, so

C

must remain on Lexell's circle.

Cyclic quadrilateral

(1827) wrote a proof in similar style to Lexell's, also using Girard's theorem, but demonstrating the angle invariants in the triangle

\triangle A^* B^* C

by constructing a

cyclic quadrilateral In geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral (four-sided polygon) whose vertex (geometry), vertices all lie on a single circle, making the sides Chord (geometry), chords of the circle. This circle is called ...

inside the Lexell circle, using the property that pairs of opposite angles in a spherical cyclic quadrilateral have the same sum. Starting with a triangle

\triangle ABC

, let

l

be the Lexell circle circumscribing

\triangle A^* B^* C,

and let

D

be another point on

l

separated from

C

by the great circle

B^* A^*\!.

Let

\alpha_1 = \angle C A^* B^*\!,

\beta_1 = \angle A^* B^* C,

\alpha_2 = \angle B^* A^* D,

\beta_2 = \angle D A^* B^*\!.

Because the quadrilateral

\square A^* D B^* C

is cyclic, the sum of each pair of its opposite angles is equal,

\angle C + \angle D = \!

\alpha_1 + \alpha_2 + \beta_1 + \beta_2,

or rearranged

\alpha_1 + \beta_1 - \angle C = \!

\angle D - \alpha_2 - \beta_2.

By Girard's theorem the spherical excess

\varepsilon

\triangle ABC

is :

&= \pi - (\angle D - \alpha_2 - \beta_2). \end

The quantity

\angle D - \alpha_2 - \beta_2

does not depend on the choice of

C,

so is invariant when

C

is moved to another point on the same arc of

l.

Therefore

\varepsilon

is also invariant. Conversely, if

C

is changed but

\varepsilon

is invariant, then the opposite angles of the quadrilateral

\square A^* D B^* C

will have the same sum, which implies

C

lies on the small circle

A^* D B^*\!.

Spherical parallelograms

Euler in 1778 proved Lexell's theorem analogously to Euclid's proof of ''Elements'' I.35 and I.37, as did

Victor-Amédée Lebesgue Victor-Amédée Lebesgue, sometimes written Le Besgue, (2 October 1791, Grandvilliers (Oise) – 10 June 1875, Bordeaux (Gironde)) was a mathematician working on number theory. He was elected a member of the Académie des sciences in 1847. See ...

independently in 1855, using spherical parallelograms – spherical quadrilaterals with congruent opposite sides, which have parallel small circles passing through opposite pairs of adjacent vertices and are in many ways analogous to Euclidean parallelograms. There is one complication compared to Euclid's proof, however: The four sides of a spherical parallelogram are the great-circle arcs through the vertices rather than the parallel small circles. Euclid's proof does not need to account for the small lens-shaped regions sandwiched between the great and small circles, which vanish in the planar case. Spherical analog of Elements I

A lemma analogous to ''Elements'' I.35: two spherical parallelograms on the same base and between the same parallels have equal area. ''Proof'': Let

\square ABC_1D_1

and

\square ABC_2D_2

be spherical parallelograms with the great circle

m

(the "midpoint circle") passing through the midpoints of sides

BC_1

and

AD_1

coinciding with the corresponding midpoint circle in

\square ABC_2D_2.

Let

F

be the intersection point between sides

AD_2

and

BC_1.

Because the midpoint circle

m

is shared, the two top sides

C_1D_1

and

C_2D_2

lie on the same small circle

l

parallel to

m

and antipodal to a small circle

l^*

passing through

A

and

B.

Two arcs of

l

are congruent,

D_1D_2 \cong C_1C_2,

thus the two curvilinear triangles

\triangle BC_1C_2

and

\triangle AD_1D_2,

each bounded by

l

on the top side, are congruent. Each parallelogram is formed from one of these curvilinear triangles added to the triangle

\triangle ABF

and to one of the congruent lens-shaped regions between each top side and

l,

with the curvilinear triangle

\triangle D_2C_1F

cut away. Therefore the parallelograms have the same area. (As in ''Elements'', the case where the parallelograms do not intersect on the sides is omitted, but can be proven by a similar argument.) ''Proof of Lexell's theorem'': Given two spherical triangles

\triangle ABC_1

and

\triangle ABC_2

each with its apex on the same small circle

l

through points

A^*

and

B^*\!,

construct new segments

C_1D_1

and

C_2D_2

congruent to

AB

with vertices

D_1

and

D_2

l.

The two quadrilaterals

\square ABC_1D_1

and

\square ABC_2D_2

are spherical parallelograms, each formed by pasting together the respective triangle and a congruent copy. By the lemma, the two parallelograms have the same area, so the original triangles must also have the same area. ''Proof of the converse'': If two spherical triangles have the same area and the apex of the second is assumed to not lie on the Lexell circle of the first, then the line through one side of the second triangle can be intersected with the Lexell circle to form a new triangle which has a different area from the second triangle but the same area as the first triangle, a contradiction. This argument is the same as that found in ''Elements'' I.39.

Saccheri quadrilateral

Another proof using the midpoint circle which is more visually apparent in a single picture is due to

(1841), who constructs the

Saccheri quadrilateral A Saccheri quadrilateral is a quadrilateral with two equal sides perpendicular to the base. It is named after Giovanni Gerolamo Saccheri, who used it extensively in his 1733 book (''Euclid freed of every flaw''), an attempt to prove the parall ...

(a quadrilateral with two adjacent right angles and two other equal angles) formed between the side of the triangle and its perpendicular projection onto the midpoint circle which has the same area as the triangle. Let

m

be the great circle through the midpoints

M_1

AC

and

M_2

BC,

and let

A',

B',

and

C'

be the perpendicular projections of the triangle vertices onto

m.

The resulting pair of right triangles

\triangle AA'M_1

and

\triangle CC'M_1

(shaded red) have equal angles at

M_1

(

vertical angles In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight lines at a point. Formally, an angle is a figure lying in a plane formed by two rays, called the '' sides'' of the angle, sharing ...

) and equal

hypotenuse In geometry, a hypotenuse is the side of a right triangle opposite to the right angle. It is the longest side of any such triangle; the two other shorter sides of such a triangle are called '' catheti'' or ''legs''. Every rectangle can be divided ...

s, so they are

congruent Congruence may refer to: Mathematics * Congruence (geometry), being the same size and shape * Congruence or congruence relation, in abstract algebra, an equivalence relation on an algebraic structure that is compatible with the structure * In modu ...

; so are the triangles

\triangle BB'M_2

and

\triangle CC'M_2

(blue). Therefore, the area of triangle

\triangle ABC

is equal to the area of Saccheri quadrilateral

\square ABB'A',

as each consists of one red triangle, one blue triangle, and the green quadrilateral

\square ABM_2M_1

pasted together. (If

C'

falls outside the arc

A'B',

then either the red or blue triangles will have negative signed area.) Because the great circle

m,

and therefore the quadrilateral

\square ABB'A',

is the same for any choice of

C

lying on the Lexell circle

l,

the area of the corresponding triangle

\triangle ABC

is constant.

Stereographic projection

The

stereographic projection In mathematics, a stereographic projection is a perspective transform, perspective projection of the sphere, through a specific point (geometry), point on the sphere (the ''pole'' or ''center of projection''), onto a plane (geometry), plane (th ...

maps the sphere to the plane. A designated great circle is mapped onto the ''primitive circle'' in the plane, and its poles are mapped to the origin (center of the primitive circle) and the

point at infinity In geometry, a point at infinity or ideal point is an idealized limiting point at the "end" of each line. In the case of an affine plane (including the Euclidean plane), there is one ideal point for each pencil of parallel lines of the plane. Ad ...

, respectively. Every circle on the sphere is mapped to a circle or straight line in the plane, with straight lines representing circles through the second pole. The stereographic projection is conformal, meaning it preserves angles. To prove relationships about a general spherical triangle

\triangle ABC,

without loss of generality ''Without loss of generality'' (often abbreviated to WOLOG, WLOG or w.l.o.g.; less commonly stated as ''without any loss of generality'' or ''with no loss of generality'') is a frequently used expression in mathematics. The term is used to indicat ...

vertex

A

can be taken as the point which projects to the origin. The sides of the spherical triangle then project to two straight segments and a circular arc. If the tangent lines to the circular side at the other two vertices intersect at point

E,

a planar straight-sided quadrilateral

\square ABEC

can be formed whose external angle at

E

is the spherical excess

\varepsilon = \angle A + \angle B + \angle C - \pi

of the spherical triangle. This is sometimes called the Cesàro method of spherical trigonometry, after crystallographer who popularized it in two 1905 papers.

(in 1855, a half century before Cesàro), and independently Aleksander Simonič (2019), used Cesàro's method to prove Lexell's theorem. Let

O

be the center in the plane of the circular arc to which side

BC

projects. Then

\square OBEC

is a

right kite In Euclidean geometry, a right kite is a kite (a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are adjacent to each other) that can be inscribed in a circle.Michael de Villiers, ''Some Adventures in Eucl ...

, so the central angle

\angle BOC

is equal to the external angle at

E,

the triangle's spherical excess

\varepsilon.

Planar angle

\angle BB^*C

is an inscribed angle subtending the same arc, so by the

inscribed angle theorem In geometry, an inscribed angle is the angle formed in the interior of a circle when two chords intersect on the circle. It can also be defined as the angle subtended at a point on the circle by two given points on the circle. Equivalently, an ...

has measure

\tfrac12\varepsilon.

This relationship is preserved for any choice of therefore, the spherical excess of the triangle is constant whenever

C

remains on the Lexell circle

l,

which projects to a line through

B^*

in the plane. (If the area of the triangle is greater than a half-hemisphere, a similar argument can be made, but the point

E

is no longer internal to the angle

Perimeter of the polar triangle

Every spherical triangle has a

dual Dual or Duals may refer to: Paired/two things * Dual (mathematics), a notion of paired concepts that mirror one another ** Dual (category theory), a formalization of mathematical duality *** see more cases in :Duality theories * Dual number, a nu ...

, its

polar triangle Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are grea ...

; if triangle

\triangle A'B'C'

(shaded purple) is the polar triangle of

\triangle ABC

(shaded orange) then the vertices

A'\!, B'\!, C'

are the poles of the respective sides

BC, CA, AB,

and vice versa, the vertices

A, B, C

are the poles of the sides

B'C'\!, C'A'\!, A'B'\!.

The polar duality exchanges the sides (

central angle A central angle is an angle whose apex (vertex) is the center O of a circle and whose legs (sides) are radii intersecting the circle in two distinct points A and B. Central angles are subtended by an arc between those two points, and the arc l ...

s) and

external angle In geometry, an angle of a polygon is formed by two adjacent sides. For a simple polygon (non-self-intersecting), regardless of whether it is convex or non-convex, this angle is called an internal angle (or interior angle) if a point withi ...

s (dihedral angles) between the two triangles. Because each side of the dual triangle is the supplement of an internal angle of the original triangle, the spherical excess

\varepsilon

\triangle ABC

is a function of the perimeter

p'

of the dual triangle :

&= 2\pi - p', \end

where the notation

, PQ,

means the angular length of the great-circle arc

PQ.

In 1854

– and independently

László Fejes Tóth László Fejes Tóth (, ; 12 March 1915 – 17 March 2005) was a Hungarian mathematician who specialized in geometry. He proved that a lattice pattern is the most efficient way to pack centrally symmetric convex sets on the Euclidean plane (a ge ...

(1953) – used the polar triangle in his proof of Lexell's theorem, which is essentially dual to the proof by isosceles triangles above, noting that under polar duality the Lexell circle

l

circumscribing

\triangle A^* B^* C

becomes an

excircle In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches (is tangent to) the three sides. The center of the incircle is a triangle center called the triangle's incenter. ...

l'

\triangle A'B'C'

(

incircle In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches (is tangent to) the three sides. The center of the incircle is a triangle center called the triangle's incenter ...

of a colunar triangle) externally tangent to side

A'B'.

If vertex

C

is moved along

l,

the side

A'B'

changes but always remains tangent to the same circle

l'.

Because the arcs from each vertex to either adjacent touch point of an incircle or excircle are congruent,

A'T_B \cong A'T_C

(blue segments) and

B'T_A \cong B'T_C

(red segments), the perimeter

p'

is :

&= , C'T_B, + , C'T_A, , \end

which remains constant, depending only on the circle

l'

but not on the changing side

A'B'.

Conversely, if the point

C

moves off of

l,

the associated excircle

l'

will change in size, moving the points

T_A

and

T_B

both toward or both away from

C'^*

and changing the perimeter

p'

\triangle A'B'C'\!

and thus changing

\varepsilon.

The locus of points

C

for which

\varepsilon

is constant is therefore

l.

Trigonometric proofs

Both Lexell () and Euler (1778) included trigonometric proofs in their papers, and several later mathematicians have presented trigonometric proofs, including

(1800), Louis Puissant (1842), Ignace-Louis-Alfred Le Cointe (1858), and Joseph-Alfred Serret (1862). Such proofs start from known triangle relations such as the

spherical law of cosines In spherical trigonometry, the law of cosines (also called the cosine rule for sides) is a theorem relating the sides and angles of spherical triangles, analogous to the ordinary law of cosines from plane trigonometry. Given a unit sphere, a "sp ...

or a formula for spherical excess, and then proceed by algebraic manipulation of

trigonometric identities In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involvin ...

Opposite arcs of Lexell's circle

The sphere is separated into two hemispheres by the great circle

AB,

and any Lexell circle through

A^*

and

B^*

is separated into two arcs, one in each hemisphere. If the point

X

is on the opposite arc from

C,

then the areas of

\triangle ABC

and

\triangle ABX

will generally differ. However, if spherical surface area is interpreted to be signed, with sign determined by boundary orientation, then the areas of triangle

\triangle ABC

and

\triangle ABX

have opposite signs and differ by the area of a hemisphere. Lexell suggested a more general framing. Given two distinct non-antipodal points

A

and

B,

there are two great-circle arcs joining them: one shorter than a semicircle and the other longer. Given a

triple Triple is used in several contexts to mean "threefold" or a " treble": Sports * Triple (baseball), a three-base hit * A basketball three-point field goal * A figure skating jump with three rotations * In bowling terms, three strikes in a row * I ...

A,B, C

of points, typically

\triangle ABC

is interpreted to mean the area enclosed by the three shorter arcs joining each pair. However, if we allow choice of arc for each pair, then 8 distinct generalized spherical triangles can be made, some with self intersections, of which four might be considered to have the same base

AB.

These eight triangles do not all have the same surface area, but if area is interpreted to be signed, with sign determined by boundary orientation, then those which differ differ by the area of a hemisphere. In this context, given four distinct, non-antipodal points

A,

B,

C,

and

X

on a sphere, Lexell's theorem holds that the signed surface area of any generalized triangle

\triangle ABC

differs from that of any generalized triangle

\triangle ABX

by a whole number of hemispheres if and only if

A^*\!,

B^*\!,

C,

and

X

are

concyclic In geometry, a set of points are said to be concyclic (or cocyclic) if they lie on a common circle. A polygon whose vertices are concyclic is called a cyclic polygon, and the circle is called its ''circumscribing circle'' or ''circumcircle''. ...

Special cases

Lunar degeneracy

As the apex

C

approaches either of the points antipodal to the base vertices – say

B^*

– along Lexell's circle

l,

in the limit the triangle

degenerates Degenerates is a musical group which originated in Grosse Pointe Park, Michigan in 1979, during the formative years of the Detroit hardcore scene. The group predated the Process of Elimination EP, which some reviewers view as the beginning of ...

to a

lune Lune may refer to: Rivers *River Lune, in Lancashire and Cumbria, England *River Lune, Durham, in County Durham, England *Lune (Weser), a 43 km-long tributary of the Weser in Germany *Lune River (Tasmania), in south-eastern Tasmania, Australia Pl ...

tangent to

l

B^*

and tangent to the antipodal small circle

l^*

B,

and having the same excess

\varepsilon

as any of the triangles with apex on the same arc of

l.

As a degenerate triangle, it has a straight angle at

A

(i.e.

\angle A = \pi,

a half turn) and equal angles

B = B^* = \tfrac12\varepsilon.

C

approaches

B^*

from the opposite direction (along the other arc of Lexell's circle), in the limit the triangle degenerates to the co-hemispherical lune tangent to the Lexell circle at

B^*

with the opposite orientation and angles

\angle B = \angle B^\star = \pi - \tfrac12\varepsilon.

Half-hemisphere area

The area of a spherical triangle is equal to half a hemisphere (excess if and only if the Lexell circle

A^*B^*C

orthogonal In mathematics, orthogonality (mathematics), orthogonality is the generalization of the geometric notion of ''perpendicularity''. Although many authors use the two terms ''perpendicular'' and ''orthogonal'' interchangeably, the term ''perpendic ...

to the great circle

AB,

that is if arc

A^*B^*

is a diameter of circle

A^*B^*C

and arc

AB

is a diameter of

ABC^*\!.

In this case, letting

D

be the point diametrically opposed to

C

on the Lexell circle

A^*B^*C

then the four triangles

\triangle ABC,

\triangle BAD,

\triangle CDA,

and

\triangle DCB

are congruent, and together form a spherical disphenoid

ABCD

(the central projection of a

disphenoid In geometry, a disphenoid () is a tetrahedron whose four faces are congruent acute-angled triangles. It can also be described as a tetrahedron in which every two edges that are opposite each other have equal lengths. Other names for the same ...

onto a concentric sphere). The eight points

AA^*BB^*CC^*DD^*

are the vertices of a

rectangular cuboid A rectangular cuboid is a special case of a cuboid with rectangular faces in which all of its dihedral angles are right angles. This shape is also called rectangular parallelepiped or orthogonal parallelepiped. Many writers just call these ...

Related concepts and results

Spherical parallelogram

A '' spherical parallelogram'' is a spherical quadrilateral

\square ABCD

whose opposite sides and opposite angles are congruent

BC \cong DA,

\angle A = \angle C,

It is in many ways analogous to a planar

parallelogram In Euclidean geometry, a parallelogram is a simple polygon, simple (non-list of self-intersecting polygons, self-intersecting) quadrilateral with two pairs of Parallel (geometry), parallel sides. The opposite or facing sides of a parallelogram a ...

. The two diagonals

AC

and

BD

bisect each-other and the figure has 2-fold

rotational symmetry Rotational symmetry, also known as radial symmetry in geometry, is the property a shape (geometry), shape has when it looks the same after some rotation (mathematics), rotation by a partial turn (angle), turn. An object's degree of rotational s ...

about the intersection point (so the diagonals each split the parallelogram into two congruent spherical triangles,

\triangle ABC \cong \triangle CDA

and if the midpoints of either pair of opposite sides are connected by a great circle

m

, the four vertices fall on two parallel small circles equidistant from it. More specifically, any vertex (say of the spherical parallelogram lies at the intersection of the two Lexell circles (

l_

and

l_

) passing through one of the adjacent vertices and the points antipodal to the other two vertices. As with spherical triangles, spherical parallelograms with the same base and the apex vertices lying on the same Lexell circle have the same area; see above. Starting from any spherical triangle, a second congruent triangle can be formed via a (spherical) point reflection across the midpoint of any side. When combined, these two triangles form a spherical parallelogram with twice the area of the original triangle.

Sorlin's theorem (polar dual)

The polar dual to Lexell's theorem, sometimes called ''Sorlin's theorem'' after A. N. J. Sorlin who first proved it trigonometrically in 1825, holds that for a spherical trilateral

\triangle abc

with sides on fixed great circles

a, b

(thus fixing the angle between them) and a fixed perimeter

p = , a,  + , b,  + , c,

(where

, a,

means the length of the triangle side the

envelope An envelope is a common packaging item, usually made of thin, flat material. It is designed to contain a flat object, such as a letter (message), letter or Greeting card, card. Traditional envelopes are made from sheets of paper cut to one o ...

of the third side

c

is a small circle internally tangent to

a, b

and externally tangent to

c,

the

to trilateral

\triangle abc.

Joseph-Émile Barbier later wrote a geometrical proof (1864) which he used to prove Lexell's theorem, by duality; see above. This result also applies in Euclidean and hyperbolic geometry: Barbier's geometrical argument can be transplanted directly to the Euclidean or hyperbolic plane.

Foliation of the sphere

Lexell's loci for any base

AB

make a ''

foliation In mathematics (differential geometry), a foliation is an equivalence relation on an topological manifold, ''n''-manifold, the equivalence classes being connected, injective function, injectively immersed submanifolds, all of the same dimension ...

'' of the sphere (decomposition into one-dimensional ''leaves''). These loci are arcs of small circles with endpoints at

A^*

and

B^*\!,

on which any intermediate point

C

is the apex of a triangle

ABC

of a fixed signed area. That area is twice the signed angle between the Lexell circle and the great circle

ABA^*B^*

at either of the points

A^*

or see above. In the figure, the Lexell circles are in green, except for those whose triangles' area is a multiple of a half hemisphere, which are black, with area labeled; see above. These Lexell circles through

A^*

and

B^*

are the spherical analog of the family of

Apollonian circles In geometry, Apollonian circles are two families (pencils) of circles such that every circle in the first family intersects every circle in the second family orthogonally, and vice versa. These circles form the basis for bipolar coordinates. T ...

through two points in the plane.

Maximizing spherical triangle area subject to constraints

In 1784

Nicolas Fuss Nicolas Fuss (29 January 1755 – 4 January 1826), also known as Nikolai Fuss, was a Swiss mathematician, living most of his life in Russia. Biography Fuss was born in Basel, Switzerland. He moved to Saint Petersburg to serve as a mathematical a ...

posed and solved the problem of finding the triangle

\triangle ABC

of maximal area on a given base

AB

with its apex

C

on a given great circle

g.

Fuss used an argument involving infinitesimal variation of

C,

but the solution is also a straightforward corollary of Lexell's theorem: the Lexell circle

A^*B^*C

through the apex must be tangent to

g

C.

g

crosses the great circle through

AB

at a point

P

, then by the spherical analog of the tangent–secant theorem, the angular distance

PC

to the desired point of tangency satisfies :

\tan^2 \tfrac12, PC,  = \tan \tfrac12 , PA^*, \,\tan \tfrac12 , PB^*, ,

from which we can explicitly construct the point

C

g

such that

\triangle ABC

has maximum area. In 1786

Theodor von Schubert Friedrich Theodor von Schubert (30 October 1758 – 21 October 1825) was a German astronomer and geographer. Life and works Born in Helmstedt, his father, Johann Ernst Schubert, was a professor of theology and abbot of Michaelstein Abbey. ...

posed and solved the problem of finding the spherical triangles of maximum and minimum area of a given base and altitude (the spherical length of a perpendicular dropped from the apex to the great circle containing the base); spherical triangles with constant altitude have their apex on a common small circle (the "altitude circle") parallel to the great circle containing the base. Schubert solved this problem by a calculus-based trigonometric approach to show that the triangle of minimal area has its apex at the nearest intersection of the altitude circle and the perpendicular bisector of the base, and the triangle of maximal area has its apex at the far intersection. However, this theorem is also a straightforward corollary of Lexell's theorem: the Lexell circles through the points antipodal to the base vertices representing the smallest and largest triangle areas are those tangent to the altitude circle. In 2019 Vincent Alberge and Elena Frenkel solved the analogous problem in the hyperbolic plane.

Steiner's theorem on area bisectors

In the Euclidean plane, a

median The median of a set of numbers is the value separating the higher half from the lower half of a Sample (statistics), data sample, a statistical population, population, or a probability distribution. For a data set, it may be thought of as the “ ...

of a triangle is the line segment connecting a vertex to the midpoint of the opposite side. The three medians of a triangle all intersect at its

centroid In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the figure. The same definition extends to any object in n-d ...

. Each median bisects the triangle's area. On the sphere, a median of a triangle can also be defined as the great-circle arc connecting a vertex to the midpoint of the opposite side. The three medians all intersect at a point, the central projection onto the sphere of the triangle's extrinsic centroid – that is, centroid of the flat triangle containing the three points if the sphere is embedded in 3-dimensional Euclidean space. However, on the sphere the great-circle arc through one vertex and a point on the opposite side which bisects the triangle's area is, in general, distinct from the corresponding median.

used Lexell's theorem to prove that these three area-bisecting arcs (which he called "equalizers") all intersect in a point, one possible alternative analog of the planar centroid in spherical geometry. (A different spherical analog of the centroid is the apex of three triangles of equal area whose bases are the sides of the original triangle, the point with

\bigl(\tfrac13,\tfrac13,\tfrac13\bigr)

as its spherical area coordinates.), , . includes another proof of this theorem without relying on Lexell's theorem.

Spherical area coordinates

The

barycentric coordinate system In geometry, a barycentric coordinate system is a coordinate system in which the location of a point is specified by reference to a simplex (a triangle for points in a plane, a tetrahedron for points in three-dimensional space, etc.). The ba ...

for points relative to a given triangle in

affine space In mathematics, an affine space is a geometric structure that generalizes some of the properties of Euclidean spaces in such a way that these are independent of the concepts of distance and measure of angles, keeping only the properties relat ...

does not have a perfect analogy in spherical geometry; there is no single spherical coordinate system sharing all of its properties. One partial analogy is ''spherical area coordinates'' for a point

P

relative to a given spherical triangle

\triangle ABC,

\left(
\frac,
\frac,
\frac
\right),

where each quantity

\varepsilon_

is the signed spherical excess of the corresponding spherical triangle

\triangle QRS.

These coordinates sum to

1,

and using the same definition in the plane results in barycentric coordinates. By Lexell's theorem, the locus of points with one coordinate constant is the corresponding Lexell circle. It is thus possible to find the point corresponding to a given triple of spherical area coordinates by intersecting two small circles. Using their respective spherical area coordinates, any spherical triangle can be mapped to any other, or to any planar triangle, using corresponding barycentric coordinates in the plane. This can be used for polyhedral

map projection In cartography, a map projection is any of a broad set of Transformation (function) , transformations employed to represent the curved two-dimensional Surface (mathematics), surface of a globe on a Plane (mathematics), plane. In a map projection, ...

s; for the definition of

discrete global grid A discrete global grid (DGG) is a mosaic that covers the entire Earth's surface. Mathematically it is a space partitioning: it consists of a set of non-empty regions that form a partition of the Earth's surface. In a usual grid-modeling strateg ...

s; or for parametrizing triangulations of the sphere or

texture mapping Texture mapping is a term used in computer graphics to describe how 2D images are projected onto 3D models. The most common variant is the UV unwrap, which can be described as an inverse paper cutout, where the surfaces of a 3D model are cut ap ...

any triangular mesh topologically equivalent to a sphere.

Euclidean plane

The analog of Lexell's theorem in the Euclidean plane comes from antiquity, and can be found in Book I of Euclid's ''Elements'', propositions 37 and 39, built on proposition 35. In the plane, Lexell's circle degenerates to a straight line (which could be called ''Lexell's line'') parallel to the base. ''Elements'' I.35 holds that parallelograms with the same base whose top sides are colinear have equal area. ''Proof'': Let the two parallelograms be

\square ABC_1D_1

and

\square ABC_2D_2,

with common base

AB

and

C_1,

D_1,

C_2,

and

D_2

on a common line parallel to the base, and let

F

be the intersection between

BC_1

and

AD_2.

Then the two top sides are congruent

C_1D_1 \cong C_2D_2

so, adding the intermediate segment to each,

C_1C_2 \cong D_1D_2.

Therefore the two triangles

\triangle BC_1C_2

and

\triangle AD_1D_2

have matching sides so are congruent. Now each of the parallelograms is formed from one of these triangles, added to the triangle

\triangle ABF

with the triangle

\triangle D_2C_1F

cut away, so therefore the two parallelograms

\square ABC_1D_1

and

\square ABC_2D_2

have equal area. ''Elements'' I.37 holds that triangles with the same base and an apex on the same line parallel to the base have equal area. ''Proof'': Let triangles

\triangle ABC_1

and

\triangle ABC_2

each have its apex on the same line

l

parallel to the base

AB.

Construct new segments

C_1D_1

and

C_2D_2

congruent to

AB

with vertices

D_1

and

D_2

l.

The two quadrilaterals

\square ABC_1D_1

and

\square ABC_2D_2

are parallelograms, each formed by pasting together the respective triangle and a congruent copy. By I.35, the two parallelograms have the same area, so the original triangles must also have the same area. ''Elements'' I.39 is the converse: two triangles of equal area on the same side of the same base have their apexes on a line parallel to the base. ''Proof'': If two triangles have the same base and same area and the apex of the second is assumed to not lie on the line parallel to the base (the "Lexell line") through the first, then the line through one side of the second triangle can be intersected with the Lexell line to form a new triangle which has a different area from the second triangle but the same area as the first triangle, a contradiction. In the Euclidean plane, the area

\varepsilon

of triangle

\triangle ABC

can be computed using any side length (the ''base'') and the distance between the line through the base and the parallel line through the apex (the corresponding ''height''). Using point

C

as the apex, and multiplying both sides of the traditional identity by

\tfrac12

to make the analogy to the spherical case more obvious, this is: :

\tfrac12 \varepsilon = \tfrac12 c\,\tfrac12 h_c.

The Euclidean theorem can be taken as a corollary of Lexell's theorem on the sphere. It is the limiting case as the curvature of the sphere approaches zero, i.e. for spherical triangles as which are infinitesimal in proportion to the radius of the sphere.

Hyperbolic plane

In the

hyperbolic plane In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai– Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with: :For any given line ''R'' and point ''P' ...

, given a triangle

\triangle ABC,

the locus of a variable point

X

such that the triangle

\triangle ABX

has the same area as

\triangle ABC

is a hypercycle passing through the points antipodal to

A

and

B,

which could be called ''Lexell's hypercycle''. Several proofs from the sphere have straightforward analogs in the hyperbolic plane, including a Gauss-style proof via a Saccheri quadrilateral by Barbarin (1902) and Frenkel & Su (2019), an Euler-style proof via hyperbolic parallelograms by Papadopoulos & Su (2017), and a Paul Serret-style proof via stereographic projection by Shvartsman (2007). In spherical geometry, the ''antipodal transformation'' takes each point to its

(diametrically opposite) point. For a sphere embedded in Euclidean space, this is a

point reflection In geometry, a point reflection (also called a point inversion or central inversion) is a geometric transformation of affine space in which every point is reflected across a designated inversion center, which remains fixed. In Euclidean or ...

through the center of the sphere; for a sphere stereographically projected to the plane, it is an inversion across the primitive circle composed with a point reflection across the origin (or equivalently, an inversion in a circle of imaginary radius of the same magnitude as the radius of the primitive circle). In planar

hyperbolic geometry In mathematics, hyperbolic geometry (also called Lobachevskian geometry or János Bolyai, Bolyai–Nikolai Lobachevsky, Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with: :For a ...

, there is a similar antipodal transformation, but any two antipodal points lie in opposite branches of a double hyperbolic plane. For a hyperboloid of two sheets embedded in

Minkowski space In physics, Minkowski space (or Minkowski spacetime) () is the main mathematical description of spacetime in the absence of gravitation. It combines inertial space and time manifolds into a four-dimensional model. The model helps show how a ...

signature A signature (; from , "to sign") is a depiction of someone's name, nickname, or even a simple "X" or other mark that a person writes on documents as a proof of identity and intent. Signatures are often, but not always, Handwriting, handwritt ...

(-, +, +),

known as the

hyperboloid model In geometry, the hyperboloid model, also known as the Minkowski model after Hermann Minkowski, is a model of ''n''-dimensional hyperbolic geometry in which points are represented by points on the forward sheet ''S''+ of a two-sheeted hyperboloi ...

, the antipodal transformation is a point reflection through the center of the hyperboloid which takes each point onto the opposite sheet; in the conformal half-plane model it is a reflection across the boundary line of ideal points taking each point into the opposite half-plane; in the conformal disk model it is an

inversion Inversion or inversions may refer to: Arts * ''Inversion'' (artwork), a 2005 temporary sculpture in Houston, Texas * Inversion (music), a term with various meanings in music theory and musical set theory * ''Inversions'' (novel) by Iain M. Bank ...

across the boundary circle, taking each point in the disk to a point in its complement. As on the sphere, any generalized circle passing through a pair of antipodal points in hyperbolic geometry is a

geodesic In geometry, a geodesic () is a curve representing in some sense the locally shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a conn ...

. Analogous to the planar and spherical triangle area formulas, the hyperbolic area

\varepsilon

of the triangle can be computed in terms of the base

c

(the hyperbolic length of arc and "height"

h_c

(the hyperbolic distance between the parallel hypercycles :

\sin \tfrac12 \varepsilon = \tanh\tfrac12 c \, \tanh\tfrac12 h_c.

As in the spherical case, in the small-triangle limit this reduces to the planar formula.

Notes

References

* * * * * * * * * {{bots, deny=Citation bot Eponymous theorems of geometry Theorems about triangles and circles Area Spherical trigonometry Articles containing proofs