Klein bottle on:
[Wikipedia]
[Google]
[Amazon]
In
Image:Klein Bottle Folding 1.svg
Image:Klein Bottle Folding 2.svg
Image:Klein Bottle Folding 3.svg
Image:Klein Bottle Folding 4.svg
Image:Klein Bottle Folding 5.svg
Image:Klein Bottle Folding 6.svg
This immersion is useful for visualizing many properties of the Klein bottle. For example, the Klein bottle has no ''boundary'', where the surface stops abruptly, and it is non-orientable, as reflected in the one-sidedness of the immersion.
 The common physical model of a Klein bottle is a similar construction. The Science Museum in London has a collection of hand-blown glass Klein bottles on display, exhibiting many variations on this topological theme. The bottles were made for the museum by Alan Bennett in 1995.
The Klein bottle, proper, does not self-intersect. Nonetheless, there is a way to visualize the Klein bottle as being contained in four dimensions. By adding a fourth dimension to the three-dimensional space, the self-intersection can be eliminated. Gently push a piece of the tube containing the intersection along the fourth dimension, out of the original three-dimensional space. A useful analogy is to consider a self-intersecting curve on the plane; self-intersections can be eliminated by lifting one strand off the plane.
The common physical model of a Klein bottle is a similar construction. The Science Museum in London has a collection of hand-blown glass Klein bottles on display, exhibiting many variations on this topological theme. The bottles were made for the museum by Alan Bennett in 1995.
The Klein bottle, proper, does not self-intersect. Nonetheless, there is a way to visualize the Klein bottle as being contained in four dimensions. By adding a fourth dimension to the three-dimensional space, the self-intersection can be eliminated. Gently push a piece of the tube containing the intersection along the fourth dimension, out of the original three-dimensional space. A useful analogy is to consider a self-intersecting curve on the plane; self-intersections can be eliminated by lifting one strand off the plane.
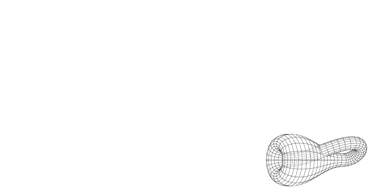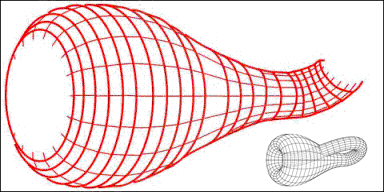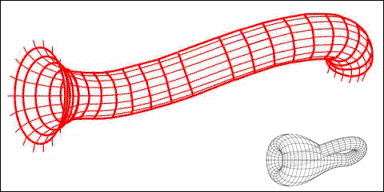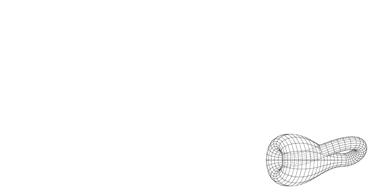 Suppose for clarification that we adopt time as that fourth dimension. Consider how the figure could be constructed in ''xyzt''-space. The accompanying illustration ("Time evolution...") shows one useful evolution of the figure. At the wall sprouts from a bud somewhere near the "intersection" point. After the figure has grown for a while, the earliest section of the wall begins to recede, disappearing like the Cheshire Cat but leaving its ever-expanding smile behind. By the time the growth front gets to where the bud had been, there is nothing there to intersect and the growth completes without piercing existing structure. The 4-figure as defined cannot exist in 3-space but is easily understood in 4-space.
More formally, the Klein bottle is the quotient space described as the
Suppose for clarification that we adopt time as that fourth dimension. Consider how the figure could be constructed in ''xyzt''-space. The accompanying illustration ("Time evolution...") shows one useful evolution of the figure. At the wall sprouts from a bud somewhere near the "intersection" point. After the figure has grown for a while, the earliest section of the wall begins to recede, disappearing like the Cheshire Cat but leaving its ever-expanding smile behind. By the time the growth front gets to where the bud had been, there is nothing there to intersect and the growth completes without piercing existing structure. The 4-figure as defined cannot exist in 3-space but is easily understood in 4-space.
More formally, the Klein bottle is the quotient space described as the
 Six colors suffice to color any map on the surface of a Klein bottle; this is the only exception to the Heawood conjecture, a generalization of the four color theorem, which would require seven.
A Klein bottle is homeomorphic to the connected sum of two projective planes. It is also homeomorphic to a sphere plus two cross-caps.
When embedded in Euclidean space, the Klein bottle is one-sided. However, there are other topological 3-spaces, and in some of the non-orientable examples a Klein bottle can be embedded such that it is two-sided, though due to the nature of the space it remains non-orientable.
Six colors suffice to color any map on the surface of a Klein bottle; this is the only exception to the Heawood conjecture, a generalization of the four color theorem, which would require seven.
A Klein bottle is homeomorphic to the connected sum of two projective planes. It is also homeomorphic to a sphere plus two cross-caps.
When embedded in Euclidean space, the Klein bottle is one-sided. However, there are other topological 3-spaces, and in some of the non-orientable examples a Klein bottle can be embedded such that it is two-sided, though due to the nature of the space it remains non-orientable.
 Dissecting a Klein bottle into halves along its plane of symmetry results in two mirror image
Dissecting a Klein bottle into halves along its plane of symmetry results in two mirror image
 :
for 0 ≤ ''u'' < π and 0 ≤ ''v'' < 2π.
:
for 0 ≤ ''u'' < π and 0 ≤ ''v'' < 2π.
Imaging Maths - The Klein Bottle
Klein Bottle animation: produced for a topology seminar at the Leibniz University Hannover.
Klein Bottle animation from 2010 including a car ride through the bottle and the original description by Felix Klein: produced at the Free University Berlin.
Klein Bottle
XScreenSaver "hack". A screensaver for X 11 and OS X featuring an animated Klein Bottle. {{Manifolds Geometric topology Manifolds Surfaces Topological spaces 1882 introductions Eponyms in geometry
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, the Klein bottle () is an example of a non-orientable surface; that is, informally, a one-sided surface which, if traveled upon, could be followed back to the point of origin while flipping the traveler upside down. More formally, the Klein bottle is a two-dimensional manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a N ...
on which one cannot define a normal vector at each point that varies continuously over the whole manifold. Other related non-orientable surfaces include the Möbius strip
In mathematics, a Möbius strip, Möbius band, or Möbius loop is a Surface (topology), surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Bened ...
and the real projective plane. While a Möbius strip is a surface with a boundary, a Klein bottle has no boundary. For comparison, a sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three ...
is an orientable surface with no boundary.
The Klein bottle was first described in 1882 by the mathematician Felix Klein.
Construction
The following square is a fundamental polygon of the Klein bottle. The idea is to 'glue' together the corresponding red and blue edges with the arrows matching, as in the diagrams below. Note that this is an "abstract" gluing, in the sense that trying to realize this in three dimensions results in a self-intersecting Klein bottle. : To construct the Klein bottle, glue the red arrows of the square together (left and right sides), resulting in a cylinder. To glue the ends of the cylinder together so that the arrows on the circles match, one would pass one end through the side of the cylinder. This creates a curve of self-intersection; this is thus an immersion of the Klein bottle in thethree-dimensional space
In geometry, a three-dimensional space (3D space, 3-space or, rarely, tri-dimensional space) is a mathematical space in which three values ('' coordinates'') are required to determine the position of a point. Most commonly, it is the three- ...
.
 The common physical model of a Klein bottle is a similar construction. The Science Museum in London has a collection of hand-blown glass Klein bottles on display, exhibiting many variations on this topological theme. The bottles were made for the museum by Alan Bennett in 1995.
The Klein bottle, proper, does not self-intersect. Nonetheless, there is a way to visualize the Klein bottle as being contained in four dimensions. By adding a fourth dimension to the three-dimensional space, the self-intersection can be eliminated. Gently push a piece of the tube containing the intersection along the fourth dimension, out of the original three-dimensional space. A useful analogy is to consider a self-intersecting curve on the plane; self-intersections can be eliminated by lifting one strand off the plane.
The common physical model of a Klein bottle is a similar construction. The Science Museum in London has a collection of hand-blown glass Klein bottles on display, exhibiting many variations on this topological theme. The bottles were made for the museum by Alan Bennett in 1995.
The Klein bottle, proper, does not self-intersect. Nonetheless, there is a way to visualize the Klein bottle as being contained in four dimensions. By adding a fourth dimension to the three-dimensional space, the self-intersection can be eliminated. Gently push a piece of the tube containing the intersection along the fourth dimension, out of the original three-dimensional space. A useful analogy is to consider a self-intersecting curve on the plane; self-intersections can be eliminated by lifting one strand off the plane.
 Suppose for clarification that we adopt time as that fourth dimension. Consider how the figure could be constructed in ''xyzt''-space. The accompanying illustration ("Time evolution...") shows one useful evolution of the figure. At the wall sprouts from a bud somewhere near the "intersection" point. After the figure has grown for a while, the earliest section of the wall begins to recede, disappearing like the Cheshire Cat but leaving its ever-expanding smile behind. By the time the growth front gets to where the bud had been, there is nothing there to intersect and the growth completes without piercing existing structure. The 4-figure as defined cannot exist in 3-space but is easily understood in 4-space.
More formally, the Klein bottle is the quotient space described as the
Suppose for clarification that we adopt time as that fourth dimension. Consider how the figure could be constructed in ''xyzt''-space. The accompanying illustration ("Time evolution...") shows one useful evolution of the figure. At the wall sprouts from a bud somewhere near the "intersection" point. After the figure has grown for a while, the earliest section of the wall begins to recede, disappearing like the Cheshire Cat but leaving its ever-expanding smile behind. By the time the growth front gets to where the bud had been, there is nothing there to intersect and the growth completes without piercing existing structure. The 4-figure as defined cannot exist in 3-space but is easily understood in 4-space.
More formally, the Klein bottle is the quotient space described as the square
In geometry, a square is a regular polygon, regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal si ...
,1× ,1with sides identified by the relations for and for .
Properties
Like theMöbius strip
In mathematics, a Möbius strip, Möbius band, or Möbius loop is a Surface (topology), surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Bened ...
, the Klein bottle is a two-dimensional manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a N ...
which is not orientable. Unlike the Möbius strip, it is a ''closed'' manifold, meaning it is a compact manifold without boundary. While the Möbius strip can be embedded in three-dimensional Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
R3, the Klein bottle cannot. It can be embedded in R4, however.
Continuing this sequence, for example creating a 3-manifold which cannot be embedded in R4 but can be in R5, is possible; in this case, connecting two ends of a spherinder to each other in the same manner as the two ends of a cylinder for a Klein bottle, creates a figure, referred to as a "spherinder Klein bottle", that cannot fully be embedded in R4.
The Klein bottle can be seen as a fiber bundle over the circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
''S''1, with fibre ''S''1, as follows: one takes the square (modulo the edge identifying equivalence relation) from above to be ''E'', the total space, while the base space ''B'' is given by the unit interval in ''y'', modulo ''1~0''. The projection π:''E''→''B'' is then given by .
The Klein bottle can be constructed (in a four dimensional space, because in three dimensional space it cannot be done without allowing the surface to intersect itself) by joining the edges of two Möbius strips, as described in the following limerick by Leo Moser:
The initial construction of the Klein bottle by identifying opposite edges of a square shows that the Klein bottle can be given a CW complex
In mathematics, and specifically in topology, a CW complex (also cellular complex or cell complex) is a topological space that is built by gluing together topological balls (so-called ''cells'') of different dimensions in specific ways. It generali ...
structure with one 0-cell ''P'', two 1-cells ''C''1, ''C''2 and one 2-cell ''D''. Its Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic (or Euler number, or Euler–Poincaré characteristic) is a topological invariant, a number that describes a topological space's ...
is therefore . The boundary homomorphism is given by and , yielding the homology groups of the Klein bottle ''K'' to be , and for .
There is a 2-1 covering map from the torus
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanarity, coplanar with the circle. The main types of toruses inclu ...
to the Klein bottle, because two copies of the fundamental region of the Klein bottle, one being placed next to the mirror image of the other, yield a fundamental region of the torus. The universal cover of both the torus and the Klein bottle is the plane R2.
The fundamental group of the Klein bottle can be determined as the group of deck transformations of the universal cover and has the presentation
A presentation conveys information from a speaker to an audience. Presentations are typically demonstrations, introduction, lecture, or speech meant to inform, persuade, inspire, motivate, build goodwill, or present a new idea/product. Presenta ...
. It follows that it is isomorphic to , the only nontrivial semidirect product of the additive group of integers with itself.
Dissection
Möbius strip
In mathematics, a Möbius strip, Möbius band, or Möbius loop is a Surface (topology), surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Bened ...
s, i.e. one with a left-handed half-twist and the other with a right-handed half-twist (one of these is pictured on the right). Remember that the intersection pictured is not really there.
Simple-closed curves
One description of the types of simple-closed curves that may appear on the surface of the Klein bottle is given by the use of the first homology group of the Klein bottle calculated with integer coefficients. This group is isomorphic to Z×Z2. Up to reversal of orientation, the only homology classes which contain simple-closed curves are as follows: (0,0), (1,0), (1,1), (2,0), (0,1). Up to reversal of the orientation of a simple closed curve, if it lies within one of the two cross-caps that make up the Klein bottle, then it is in homology class (1,0) or (1,1); if it cuts the Klein bottle into two Möbius strips, then it is in homology class (2,0); if it cuts the Klein bottle into an annulus, then it is in homology class (0,1); and if bounds a disk, then it is in homology class (0,0).Parametrization
The figure 8 immersion
To make the "figure 8" or "bagel" immersion of the Klein bottle, one can start with aMöbius strip
In mathematics, a Möbius strip, Möbius band, or Möbius loop is a Surface (topology), surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Bened ...
and curl it to bring the edge to the midline; since there is only one edge, it will meet itself there, passing through the midline. It has a particularly simple parametrization as a "figure-8" torus with a half-twist:
:
for 0 ≤ ''θ'' < 2π, 0 ≤ ''v'' < 2π and ''r'' > 2.
In this immersion, the self-intersection circle (where sin(''v'') is zero) is a geometric circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
in the ''xy'' plane. The positive constant ''r'' is the radius of this circle. The parameter ''θ'' gives the angle in the ''xy'' plane as well as the rotation of the figure 8, and ''v'' specifies the position around the 8-shaped cross section. With the above parametrization the cross section is a 2:1 Lissajous curve.
4-D non-intersecting
A non-intersecting 4-D parametrization can be modeled after that of the flat torus: : where ''R'' and ''P'' are constants that determine aspect ratio, ''θ'' and ''v'' are similar to as defined above. ''v'' determines the position around the figure-8 as well as the position in the x-y plane. ''θ'' determines the rotational angle of the figure-8 as well and the position around the z-w plane. ''ε'' is any small constant and ''ε'' sin''v'' is a small ''v'' dependent bump in ''z-w'' space to avoid self intersection. The ''v'' bump causes the self intersecting 2-D/planar figure-8 to spread out into a 3-D stylized "potato chip" or saddle shape in the x-y-w and x-y-z space viewed edge on. When ''ε=0'' the self intersection is a circle in the z-w plane <0, 0, cos''θ'', sin''θ''>.3D pinched torus / 4D Möbius tube
The pinched torus is perhaps the simplest parametrization of the Klein bottle in both three and four dimensions. It can be viewed as a variant of a torus that, in three dimensions, flattens and passes through itself on one side. Unfortunately, in three dimensions this parametrization has two pinch points, which makes it undesirable for some applications. In four dimensions the ''z'' amplitude rotates into the ''w'' amplitude and there are no self intersections or pinch points. : One can view this as a tube or cylinder that wraps around, as in a torus, but its circular cross section flips over in four dimensions, presenting its "backside" as it reconnects, just as a Möbius strip cross section rotates before it reconnects. The 3D orthogonal projection of this is the pinched torus shown above. Just as a Möbius strip is a subset of a solid torus, the Möbius tube is a subset of a toroidally closed spherinder (solid spheritorus).Bottle shape
The following parametrization of the usual 3-dimensional immersion of the bottle itself is much more complicated. :
for 0 ≤ ''u'' < π and 0 ≤ ''v'' < 2π.
:
for 0 ≤ ''u'' < π and 0 ≤ ''v'' < 2π.
Homotopy classes
Regular 3D immersions of the Klein bottle fall into three regular homotopy classes. The three are represented by: * the "traditional" Klein bottle; * the left-handed figure-8 Klein bottle; * the right-handed figure-8 Klein bottle. The traditional Klein bottle immersion is achiral. The figure-8 immersion is chiral. (The pinched torus immersion above is not regular, as it has pinch points, so it is not relevant to this section.) If the traditional Klein bottle is cut in its plane of symmetry it breaks into two Möbius strips of opposite chirality. A figure-8 Klein bottle can be cut into two Möbius strips of the ''same'' chirality, and cannot be regularly deformed into its mirror image.Generalizations
The generalization of the Klein bottle to highergenus
Genus (; : genera ) is a taxonomic rank above species and below family (taxonomy), family as used in the biological classification of extant taxon, living and fossil organisms as well as Virus classification#ICTV classification, viruses. In bino ...
is given in the article on the fundamental polygon.
In another order of ideas, constructing 3-manifolds, it is known that a solid Klein bottle is homeomorphic to the Cartesian product
In mathematics, specifically set theory, the Cartesian product of two sets and , denoted , is the set of all ordered pairs where is an element of and is an element of . In terms of set-builder notation, that is
A\times B = \.
A table c ...
of a Möbius strip
In mathematics, a Möbius strip, Möbius band, or Möbius loop is a Surface (topology), surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Bened ...
and a closed interval. The ''solid Klein bottle'' is the non-orientable version of the solid torus, equivalent to
See also
*Algebraic topology
Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariant (mathematics), invariants that classification theorem, classify topological spaces up t ...
* Alice universe
* Bavard's Klein bottle systolic inequality
* Boy's surface
References
Citations
Sources
* * * (A classical on the theory of Klein surfaces) *External links
Imaging Maths - The Klein Bottle
Klein Bottle animation: produced for a topology seminar at the Leibniz University Hannover.
Klein Bottle animation from 2010 including a car ride through the bottle and the original description by Felix Klein: produced at the Free University Berlin.
Klein Bottle
XScreenSaver "hack". A screensaver for X 11 and OS X featuring an animated Klein Bottle. {{Manifolds Geometric topology Manifolds Surfaces Topological spaces 1882 introductions Eponyms in geometry