Kempe's Universality Theorem on:
[Wikipedia]
[Google]
[Amazon]
In J. Malkevich, Feature Column, American Mathematical Society.
/ref> Kempe recognized that his results demonstrate the existence of a drawing linkage but it would not be practical. He states
Automated Generation of Kempe Linkages for Algebraic Curves in a Dynamic Geometry System.
Saarland University, Saarbrucken, Germany, Faculty of Natural Sciences and Technology I, Department of Computer Science.
/ref> This has been extended to provide movement of the end-effector, but again for parameterized curves. M. Gallet, C. Koutschan, Z. Li, G. Regensburger, J. Schicho, and N. Villamiza (2017), Planar Linkages Following a Prescribed Motion
Mathematics of Computation, 86(303), pages 473-506. Specializing the curves to those defined by
J of Mechanisms and Robotics, 9(2), 024503
J of Computers and Information in Science and Engineering, 17(3)
(left) and a hypocycloid curve (right).
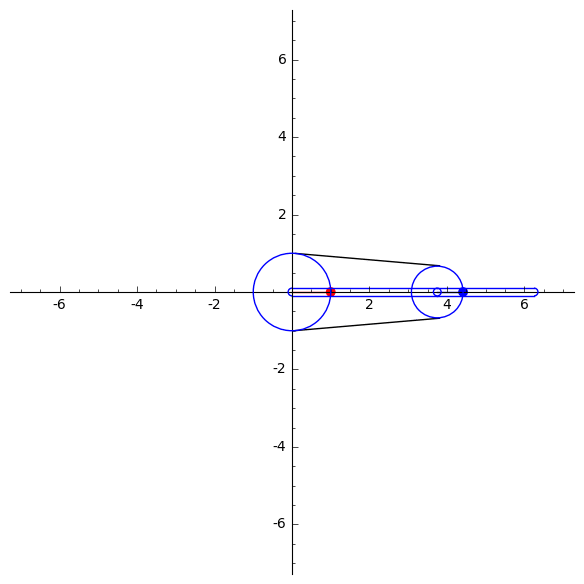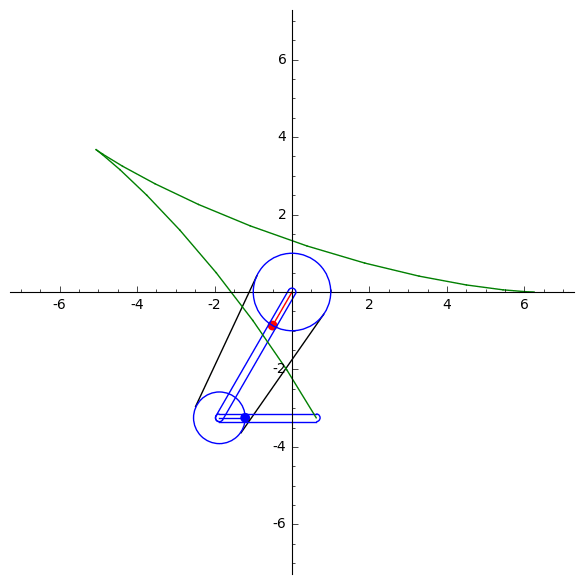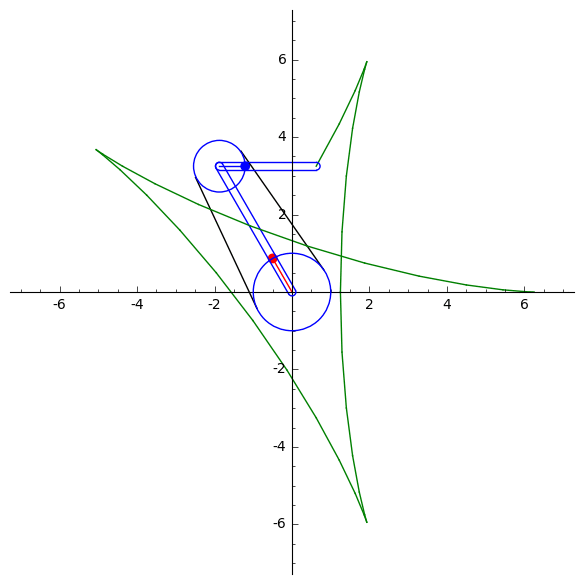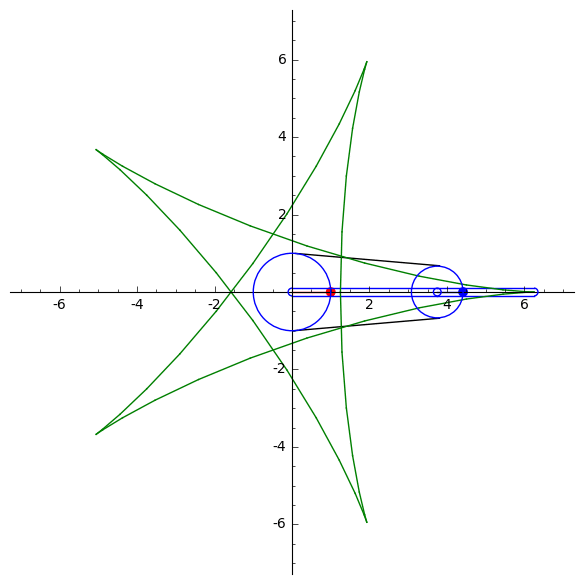
A. Kobel's animations of the parabola, self-intersecting cubic, smooth elliptic cubic and the trifolium curvesY. Liu's mechanical computation for drawing algebraic plane curvesM. Gallet et al. animations of linkages following a prescribed motionY. Liu's animations drawing trigonometric plane curves, the Butterfly mechanismLinkage that signs your nameLinkage that writes cursive Chinese
Linkages (mechanical)
algebraic geometry
Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometry, geometrical problems. Classically, it studies zero of a function, zeros of multivariate polynomials; th ...
, Kempe's universality theorem states that any bounded subset of an algebraic curve
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane cu ...
may be traced out by the motion of one of the joints in a suitably chosen linkage.
It is named for British mathematician Alfred B. Kempe, who in 1876 published his article ''On a General Method of describing Plane Curves of the nth degree by Linkwork,'' which showed that for any arbitrary algebraic plane curve, a linkage can be constructed that draws the curve. However, Kempe's proof was flawed and the first complete proof was provided in 2002 based on his ideas.
This theorem has been popularized by describing it as saying, "One can design a linkage which will sign your name!"/ref> Kempe recognized that his results demonstrate the existence of a drawing linkage but it would not be practical. He states
It is hardly necessary to add, that this method would not be practically useful on account of the complexity of the linkwork employed, a necessary consequence of the perfect generality of the demonstration.He then calls for the "mathematical artist" to find simpler ways to achieve this result:
The method has, however, an interest, as showing that there ''is'' a way of drawing any given case; and the variety of methods of expressing particular functions that have already been discovered renders it in the highest degree probable that in every case a simpler method can be found. There is still, however, a wide field open to the mathematical artist to discover the simplest linkworks that will describe particular curves.A series of animations demonstrating the linkwork that results from Kempe's universality theorem are available for the
parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactl ...
, self-intersecting cubic
Cubic may refer to:
Science and mathematics
* Cube (algebra), "cubic" measurement
* Cube, a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex
** Cubic crystal system, a crystal system w ...
, smooth elliptic cubic and the trifolium
Clovers, also called trefoils, are plants of the genus ''Trifolium'' (), consisting of about 300 species of flowering plants in the legume family Fabaceae originating in Europe. The genus has a cosmopolitan distribution with the highest diversity ...
curves.A. Kobel, (2008Automated Generation of Kempe Linkages for Algebraic Curves in a Dynamic Geometry System.
Saarland University, Saarbrucken, Germany, Faculty of Natural Sciences and Technology I, Department of Computer Science.
Simpler drawing linkages
Several approaches have been taken to simplify the drawing linkages that result from Kempe's universality theorem. Some of the complexity arises from the linkages Kempe used to perform addition and subtraction of two angles, the multiplication of an angle by a constant, and translation of the rotation of a link in one location to a rotation of a second link at another location. Kempe called these linkages additor, reversor, multiplicator and translator linkages, respectively. The drawing linkage can be simplified by using bevel gear differentials to add and subtract angles,gear train
A gear train or gear set is a machine element of a mechanical system formed by mounting two or more gears on a frame such that the teeth of the gears engage.
Gear teeth are designed to ensure the pitch circles of engaging gears roll on each oth ...
s to multiply angles and belt or cable drives to translate rotation angles.
Another source of complexity is the generality of Kempe's application to all algebraic curves. By focusing on parameterized algebraic curves, dual quaternion algebra can be used to factor the motion polynomial and obtain a drawing linkage.G.Hegedus, Z. Li, J. Schicho, H. P. Schrocker (2015), From the Fundamental Theorem of Algebra to Kempe’s Universality Theorem/ref> This has been extended to provide movement of the end-effector, but again for parameterized curves. M. Gallet, C. Koutschan, Z. Li, G. Regensburger, J. Schicho, and N. Villamiza (2017), Planar Linkages Following a Prescribed Motion
Mathematics of Computation, 86(303), pages 473-506. Specializing the curves to those defined by
trigonometric polynomial
In the mathematical subfields of numerical analysis and mathematical analysis, a trigonometric polynomial is a finite linear combination of functions sin(''nx'') and cos(''nx'') with ''n'' taking on the values of one or more natural numbers. The c ...
s has provided another way to obtain simpler drawing linkages.Y. Liu and J. M. McCarthy (2017), Design of Mechanisms to Draw Trigonometric Plane CurvesJ of Mechanisms and Robotics, 9(2), 024503
Bézier curve
A Bézier curve ( , ) is a parametric equation, parametric curve used in computer graphics and related fields. A set of discrete "control points" defines a smooth, continuous curve by means of a formula. Usually the curve is intended to approxima ...
s can be written in the form of trigonometric polynomial
In the mathematical subfields of numerical analysis and mathematical analysis, a trigonometric polynomial is a finite linear combination of functions sin(''nx'') and cos(''nx'') with ''n'' taking on the values of one or more natural numbers. The c ...
s therefore a linkage system can be designed that draws any curve that is approximated by a sequence of Bézier curves.Y. Liu and J. M. McCarthy (2017), Design of a Linkage System to Write in CursiveJ of Computers and Information in Science and Engineering, 17(3)
Visualizations
Below is an example of a single-coupled serial chain mechanism, designed by Liu and McCarthy, used to draw th(left) and a hypocycloid curve (right).

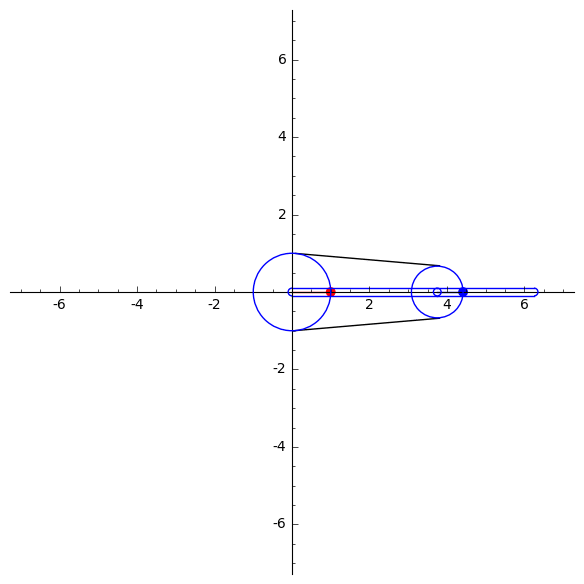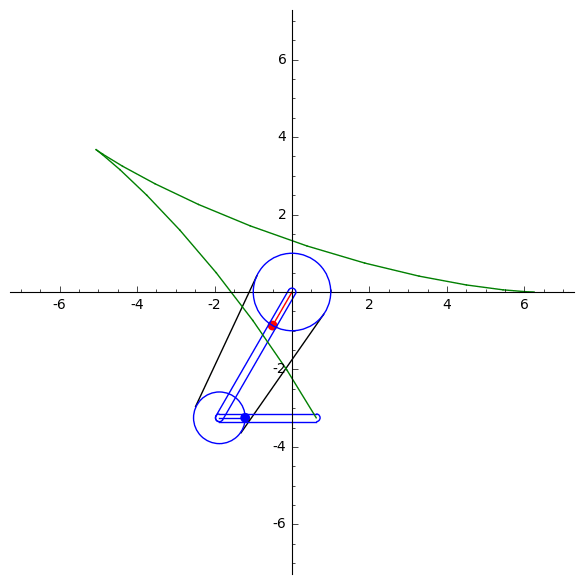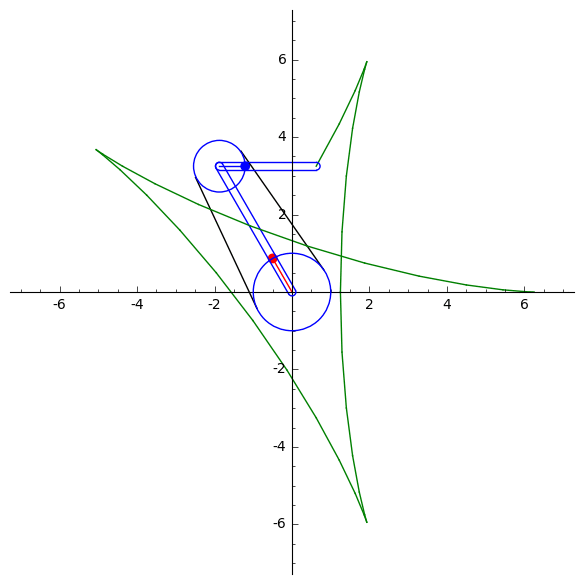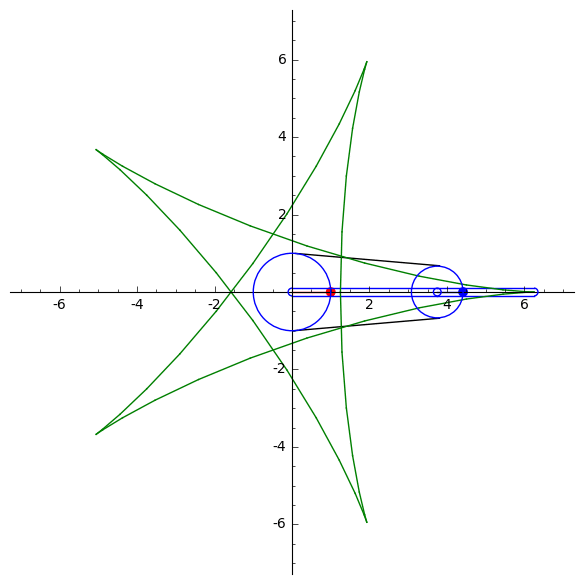
See also
*Structural rigidity
In discrete geometry and mechanics, structural rigidity is a combinatorial theory for predicting the flexibility of ensembles formed by rigid bodies connected by flexible linkages or hinges.
Definitions
Rigidity is the property of a structu ...
* Mnëv's universality theorem
In mathematics, Mnëv's universality theorem is a result in the intersection of combinatorics and algebraic geometry used to represent algebraic (or semialgebraic) varieties as realization spaces of oriented matroids.
Informally it can also be u ...
References
{{reflistExternal links
A. Kobel's animations of the parabola, self-intersecting cubic, smooth elliptic cubic and the trifolium curves
Linkages (mechanical)