Smirnov
Smirnov (masculine, ) or Smirnova (feminine, ) is one of the two most common surnames in Russia. ''Smirnov'' () is derived from an adjectival nickname (; in archaic form , ), meaning 'quiet, still, peaceful, gentle'.
Smirnov
* Aleksandr Smirnov ...
transform) is a basic method for pseudo-random number sampling
Non-uniform random variate generation or pseudo-random number sampling is the numerical practice of generating pseudo-random numbers (PRN) that follow a given probability distribution.
Methods are typically based on the availability of a unifo ...
, i.e., for generating sample numbers at random
In common usage, randomness is the apparent or actual lack of definite pattern or predictability in information. A random sequence of events, symbols or steps often has no order and does not follow an intelligible pattern or combination. ...
from any probability distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical descri ...
given its cumulative distribution function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ever ...
.
Inverse transformation sampling takes uniform samples of a number between 0 and 1, interpreted as a probability, and then returns the smallest number such that for the cumulative distribution function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ever ...
of a random variable. For example, imagine that is the standard normal distribution
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
f(x) = \frac ...
with mean zero and standard deviation one. The table below shows samples taken from the uniform distribution and their representation on the standard normal distribution.
 We are randomly choosing a proportion of the area under the curve and returning the number in the domain such that exactly this proportion of the area occurs to the left of that number. Intuitively, we are unlikely to choose a number in the far end of tails because there is very little area in them which would require choosing a number very close to zero or one.
Computationally, this method involves computing the
We are randomly choosing a proportion of the area under the curve and returning the number in the domain such that exactly this proportion of the area occurs to the left of that number. Intuitively, we are unlikely to choose a number in the far end of tails because there is very little area in them which would require choosing a number very close to zero or one.
Computationally, this method involves computing the quantile function
In probability and statistics, the quantile function is a function Q: ,1\mapsto \mathbb which maps some probability x \in ,1/math> of a random variable v to the value of the variable y such that P(v\leq y) = x according to its probability distr ...
of the distribution — in other words, computing the cumulative distribution function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ever ...
(CDF) of the distribution (which maps a number in the domain to a probability between 0 and 1) and then inverting that function. This is the source of the term "inverse" or "inversion" in most of the names for this method. Note that for a discrete distribution
In probability theory and statistics, a probability distribution is a function that gives the probabilities of occurrence of possible events for an experiment. It is a mathematical description of a random phenomenon in terms of its sample spac ...
, computing the CDF is not in general too difficult: we simply add up the individual probabilities for the various points of the distribution. For a continuous distribution
In probability theory and statistics, a probability distribution is a function that gives the probabilities of occurrence of possible events for an experiment. It is a mathematical description of a random phenomenon in terms of its sample spac ...
, however, we need to integrate the probability density function
In probability theory, a probability density function (PDF), density function, or density of an absolutely continuous random variable, is a Function (mathematics), function whose value at any given sample (or point) in the sample space (the s ...
(PDF) of the distribution, which is impossible to do analytically for most distributions (including the normal distribution
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
f(x) = \frac ...
). As a result, this method may be computationally inefficient for many distributions and other methods are preferred; however, it is a useful method for building more generally applicable samplers such as those based on rejection sampling
In numerical analysis and computational statistics, rejection sampling is a basic technique used to generate observations from a distribution. It is also commonly called the acceptance-rejection method or "accept-reject algorithm" and is a type o ...
.
For the normal distribution
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
f(x) = \frac ...
, the lack of an analytical expression for the corresponding quantile function means that other methods (e.g. the Box–Muller transform
The Box–Muller transform, by George Edward Pelham Box and Mervin Edgar Muller, is a random number sampling method for generating pairs of independent, standard, normally distributed (zero expectation, unit variance) random numbers, given a ...
) may be preferred computationally. It is often the case that, even for simple distributions, the inverse transform sampling method can be improved on: see, for example, the ziggurat algorithm
The ziggurat algorithm is an algorithm for pseudo-random number sampling. Belonging to the class of rejection sampling algorithms, it relies on an underlying source of uniformly-distributed random numbers, typically from a pseudo-random number ge ...
and rejection sampling
In numerical analysis and computational statistics, rejection sampling is a basic technique used to generate observations from a distribution. It is also commonly called the acceptance-rejection method or "accept-reject algorithm" and is a type o ...
. On the other hand, it is possible to approximate the quantile function of the normal distribution extremely accurately using moderate-degree polynomials, and in fact the method of doing this is fast enough that inversion sampling is now the default method for sampling from a normal distribution in the statistical package R.
Formal statement
For anyrandom variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a Mathematics, mathematical formalization of a quantity or object which depends on randomness, random events. The term 'random variable' in its mathema ...
, the random variable has the same distribution as , where is the generalized inverse
In mathematics, and in particular, algebra, a generalized inverse (or, g-inverse) of an element ''x'' is an element ''y'' that has some properties of an inverse element but not necessarily all of them. The purpose of constructing a generalized inv ...
of the cumulative distribution function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ever ...
of and is uniform on probability integral transform
In probability theory, the probability integral transform (also known as universality of the uniform) relates to the result that data values that are modeled as being random variables from any given continuous distribution can be converted to rando ...
, which states that for a continuous random variable
In probability theory and statistics, a probability distribution is a function that gives the probabilities of occurrence of possible events for an experiment. It is a mathematical description of a random phenomenon in terms of its sample spa ...
with cumulative distribution function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ever ...
, the random variable is uniform
A uniform is a variety of costume worn by members of an organization while usually participating in that organization's activity. Modern uniforms are most often worn by armed forces and paramilitary organizations such as police, emergency serv ...
on 
Intuition
FromThe method
 The problem that the inverse transform sampling method solves is as follows:
*Let
The problem that the inverse transform sampling method solves is as follows:
*Let random variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a Mathematics, mathematical formalization of a quantity or object which depends on randomness, random events. The term 'random variable' in its mathema ...
whose distribution can be described by the cumulative distribution function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ever ...
generalized inverse
In mathematics, and in particular, algebra, a generalized inverse (or, g-inverse) of an element ''x'' is an element ''y'' that has some properties of an inverse element but not necessarily all of them. The purpose of constructing a generalized inv ...
of the desired CDF, i.e. power series
In mathematics, a power series (in one variable) is an infinite series of the form
\sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots
where ''a_n'' represents the coefficient of the ''n''th term and ''c'' is a co ...
solutions, despite their non-linearity.
Examples
* As an example, suppose we have a random variablecumulative distribution function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ever ...
: exponential distribution
In probability theory and statistics, the exponential distribution or negative exponential distribution is the probability distribution of the distance between events in a Poisson point process, i.e., a process in which events occur continuousl ...
with 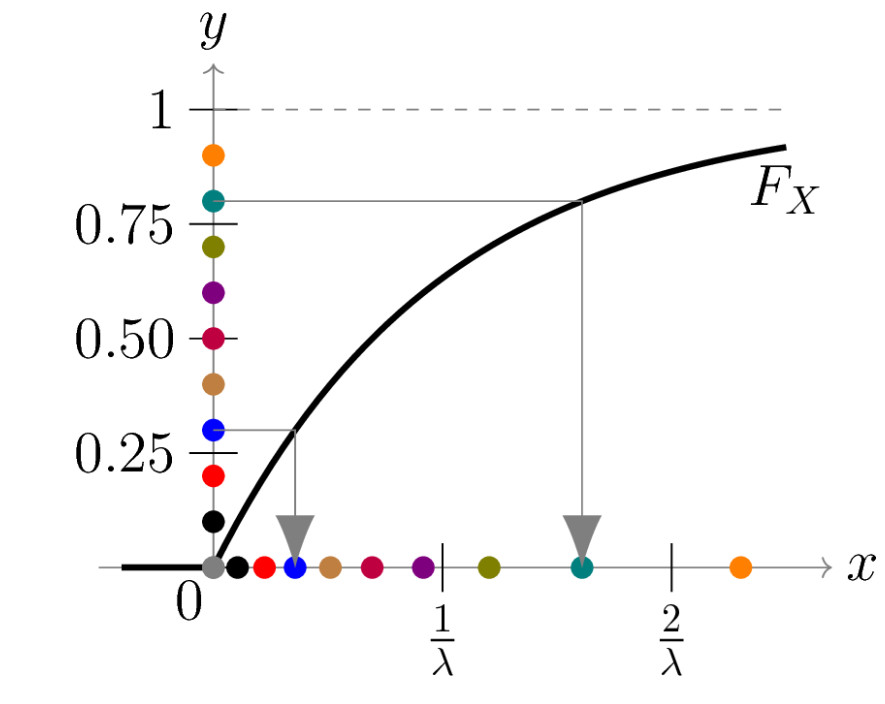 : Note that the distribution does not change if we start with 1-y instead of y. For computational purposes, it therefore suffices to generate random numbers y in
: Note that the distribution does not change if we start with 1-y instead of y. For computational purposes, it therefore suffices to generate random numbers y in , 1
The comma is a punctuation mark that appears in several variants in different languages. Some typefaces render it as a small line, slightly curved or straight, but inclined from the vertical; others give it the appearance of a miniature fille ...
and then simply calculate
: Proof of correctness
Letcumulative distribution function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ever ...
, and let infimum
In mathematics, the infimum (abbreviated inf; : infima) of a subset S of a partially ordered set P is the greatest element in P that is less than or equal to each element of S, if such an element exists. If the infimum of S exists, it is unique ...
because CDFs are weakly monotonic and right-continuous
In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as '' discontinuities''. More preci ...
):
:uniform
A uniform is a variety of costume worn by members of an organization while usually participating in that organization's activity. Modern uniforms are most often worn by armed forces and paramilitary organizations such as police, emergency serv ...
random variable on Truncated distribution
Inverse transform sampling can be simply extended to cases oftruncated distribution
In statistics, a truncated distribution is a conditional distribution that results from restricting the domain of some other probability distribution. Truncated distributions arise in practical statistics in cases where the ability to record, or ...
s on the interval Reduction of the number of inversions
In order to obtain a large number of samples, one needs to perform the same number of inversions of the distribution. One possible way to reduce the number of inversions while obtaining a large number of samples is the application of the so-called Stochastic Collocation Monte Carlo sampler (SCMC sampler) within apolynomial chaos
Polynomial chaos (PC), also called polynomial chaos expansion (PCE) and Wiener chaos expansion, is a method for representing a random variable in terms of a polynomial function of other random variables. The polynomials are chosen to be orthogonal ...
expansion framework. This allows us to generate any number of Monte Carlo samples with only a few inversions of the original distribution with independent samples of a variable for which the inversions are analytically available, for example the standard normal variable.
Software implementations
There are software implementations available for applying the inverse sampling method by using numerical approximations of the inverse in the case that it is not available in closed form. For example, an approximation of the inverse can be computed if the user provides some information about the distributions such as the PDF or the CDF. * C library UNU.RAN * R library Runuran * Python subpackage sampling in scipy.statsSee also
*Probability integral transform
In probability theory, the probability integral transform (also known as universality of the uniform) relates to the result that data values that are modeled as being random variables from any given continuous distribution can be converted to rando ...
* Copula, defined by means of probability integral transform.
* Quantile function
In probability and statistics, the quantile function is a function Q: ,1\mapsto \mathbb which maps some probability x \in ,1/math> of a random variable v to the value of the variable y such that P(v\leq y) = x according to its probability distr ...
, for the explicit construction of inverse CDFs.
* Inverse distribution function
In probability and statistics, the quantile function is a function Q: ,1\mapsto \mathbb which maps some probability x \in ,1/math> of a random variable v to the value of the variable y such that P(v\leq y) = x according to its probability distr ...
for a precise mathematical definition for distributions with discrete components.
* Rejection sampling
In numerical analysis and computational statistics, rejection sampling is a basic technique used to generate observations from a distribution. It is also commonly called the acceptance-rejection method or "accept-reject algorithm" and is a type o ...
is another common technique to generate random variates that does not rely on inversion of the CDF.
References