Instantaneous Axis Of Rotation on:
[Wikipedia]
[Google]
[Amazon]
The instant center of rotation (also known as instantaneous velocity center, instantaneous center, or pole of planar displacement) of a body undergoing planar movement is a point that has zero velocity at a particular instant of time. At this instant, the velocity vectors of the other points in the body generate a circular field around this
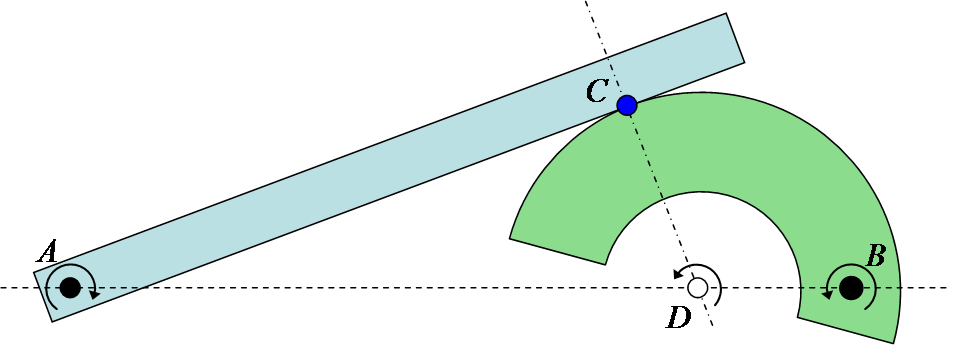 If two planar rigid bodies are in contact, and each body has its own distinct center of rotation, then the relative center of rotation between the bodies has to lie somewhere on the line connecting the two centers. As a result, since pure rolling can only exist when the center of rotation is at the point of contact (as seen above with the wheel on the road), it is only when the point of contact goes through the line connecting the two rotation centers that pure rolling can be achieved. This is known in
If two planar rigid bodies are in contact, and each body has its own distinct center of rotation, then the relative center of rotation between the bodies has to lie somewhere on the line connecting the two centers. As a result, since pure rolling can only exist when the center of rotation is at the point of contact (as seen above with the wheel on the road), it is only when the point of contact goes through the line connecting the two rotation centers that pure rolling can be achieved. This is known in
center of rotation
Rotation in mathematics is a concept originating in geometry. Any rotation is a motion of a certain space that preserves at least one point. It can describe, for example, the motion of a rigid body around a fixed point. Rotation can have a s ...
which is identical to what is generated by a pure rotation
Rotation or rotational/rotary motion is the circular movement of an object around a central line, known as an ''axis of rotation''. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersect ...
.
Planar movement of a body is often described using a plane figure moving in a two-dimensional plane. The instant center is the point in the moving plane around which all other points are rotating at a specific instant of time.
The continuous movement of a plane has an instant center for every value of the time parameter. This generates a curve called the moving centrode. The points in the fixed plane corresponding to these instant centers form the fixed centrode.
The generalization of this concept to 3-dimensional space is that of a twist around a screw. The screw has an axis which is a line in 3D space (not necessarily through the origin), the axis of rotation
Rotation or rotational/rotary motion is the circular movement of an object around a central line, known as an ''axis of rotation''. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersect ...
; the screw also has a finite pitch (a fixed translation along its axis corresponding to a rotation about the screw axis).
Pole of a planar displacement
The instant center can be considered the limiting case of the pole of a planar displacement. The planar displacement of a body from position 1 to position 2 is defined by the combination of a planarrotation
Rotation or rotational/rotary motion is the circular movement of an object around a central line, known as an ''axis of rotation''. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersect ...
and planar translation
Translation is the communication of the semantics, meaning of a #Source and target languages, source-language text by means of an Dynamic and formal equivalence, equivalent #Source and target languages, target-language text. The English la ...
. For any planar displacement there is a point in the moving body that is in the same place before and after the displacement. The displacement can be viewed as a rotation around this pole.
Construction for the pole of a planar displacement
First, select two points A and B in the moving body and locate the corresponding points in the two positions; see the illustration. Construct the perpendicular bisectors to the two segments A1A2 and B1B2. The intersection P of these two bisectors is the pole of the planar displacement. Notice that A1 and A2 lie on a circle around P. This is true for the corresponding positions of every point in the body.
If the two positions of a body are separated by an instant of time in a planar movement, then the pole of a displacement becomes the instant center. In this case, the segments constructed between the instantaneous positions of the points A and B become the velocity vectors VA and VB. The lines perpendicular to these velocity vectors intersect in the instant center.
The algebraic construction of the Cartesian coordinates can be arranged as follows: The midpoint between and
has the Cartesian coordinates
:
and the midpoint between and has the Cartesian coordinates
:
The two angles from to and from to measured counter-clockwise relative to the horizontal are determined by
:
Find the position of
Method 1:
Taking the correct branches of the:tangent In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points o .... Let the center of the rotation have distances and to the two midpoints. Assuming clockwise rotation (otherwise switch the sign of ):
Rewrite this as a 4 × 4 inhomogeneousMethod 2:system of linear equations In mathematics, a system of linear equations (or linear system) is a collection of two or more linear equations involving the same variable (math), variables. For example, : \begin 3x+2y-z=1\\ 2x-2y+4z=-2\\ -x+\fracy-z=0 \end is a system of th ...with 4 unknowns (the two distances and the two coordinates of the center): : The coordinates of the center of the rotation are the first two components of the solution vector :
Find equations of the bisectors of two segments A1A2 and B1B2 as follows The equation of a straight line in point- slope form is: where is the point and is the slope. The equation of the bisector of A1A2 is The equation of the bisector of B1B2 is These two bisectors intersect at so a system of ''2'' equations with ''2'' unknowns andPure translation If the displacement between two positions is a pure translation, then the perpendicular bisectors of the segments A1B1 and A2B2 form parallel lines. These lines are considered to intersect at a point on thecoefficients In mathematics, a coefficient is a multiplicative factor involved in some term of a polynomial, a series, or any other type of expression. It may be a number without units, in which case it is known as a numerical factor. It may also be a ...can be written The solution of this system is
line at infinity
In geometry and topology, the line at infinity is a projective line that is added to the affine plane in order to give closure to, and remove the exceptional cases from, the incidence properties of the resulting projective plane. The line at ...
, thus the pole of this planar displacement is said to "lie at infinity" in the direction of the perpendicular bisectors.
In the limit, pure translation becomes planar movement with point velocity vectors that are parallel. In this case, the instant center is said to lie at infinity in the direction perpendicular to the velocity vectors.
Instant center of a wheel rolling without slipping
Consider the planar movement of a circular wheel rolling without slipping on a linear road; see sketch 3. The wheel rotates around its axis M, which translates in a direction parallel to the road. The point of contact P of the wheel with road does not slip, which means the point P has zero velocity with respect to the road. Thus, at the instant the point P on the wheel comes in contact with the road it becomes an instant center. The set of points of the moving wheel that become instant centers is the circle itself, which defines the moving centrode. The points in the fixed plane that correspond to these instant centers is the line of the road, which defines the fixed centrode. The velocity vector of a point A in the wheel is perpendicular to the segment AP and is proportional to the length of this segment. In particular, the velocities of points in the wheel are determined by the angular velocity of the wheel in rotation around P. The velocity vectors of a number of points are illustrated in sketch 3 and can be calculated using the following equation: : where is velocity of point A, angular velocity of wheel and vector from point P to A. The further a point in the wheel is from the instant center P, the proportionally larger its speed. Therefore, the point at the top of the wheel moves in the same direction as the center M of the wheel, but twice as fast, since it is twice the distance away from P. All points that are a distance equal to the radius of the wheel 'r' from point P move at the same speed as the point M but in different directions. This is shown for a point on the wheel that has the same speed as M but moves in the direction tangent to the circle around P.Relative center of rotation for two contacting planar bodies
 If two planar rigid bodies are in contact, and each body has its own distinct center of rotation, then the relative center of rotation between the bodies has to lie somewhere on the line connecting the two centers. As a result, since pure rolling can only exist when the center of rotation is at the point of contact (as seen above with the wheel on the road), it is only when the point of contact goes through the line connecting the two rotation centers that pure rolling can be achieved. This is known in
If two planar rigid bodies are in contact, and each body has its own distinct center of rotation, then the relative center of rotation between the bodies has to lie somewhere on the line connecting the two centers. As a result, since pure rolling can only exist when the center of rotation is at the point of contact (as seen above with the wheel on the road), it is only when the point of contact goes through the line connecting the two rotation centers that pure rolling can be achieved. This is known in involute gear
The involute gear profile is the most commonly used system for gearing today, with cycloid gearing still used for some specialties such as clocks. In an involute gear, the profiles of the teeth are ''involutes of a circle.'' The involute of a ...
design as the pitch point, where there is no relative sliding between the gears. In fact, the gearing ratio between the two rotating parts is found by the ratio of the two distances to the relative center. In the example in Sketch 4 the gearing ratio is
Instant center of rotation and mechanisms
Sketch 1 above shows afour-bar linkage
In the study of Mechanism (engineering), mechanisms, a four-bar linkage, also called a four-bar, is the simplest closed-Kinematic chain, chain movable linkage (mechanical), linkage. It consists of four Rigid body, bodies, called ''bars'' or ''link ...
where a number of instant centers of rotation are illustrated. The rigid body noted by the letters BAC is connected with links P1-A and P2-B to a base or frame.
The three moving parts of this mechanism (the base is not moving) are: link P1-A, link P2-B, and body BAC. For each of these three parts an instant center of rotation may be determined.
Considering first link P1-A: all points on this link, including point A, rotate around point P1. Since P1 is the only point not moving in the given plane it may be called the instant center of rotation for this link. Point A, at distance P1-A from P1, moves in a circular motion in a direction perpendicular to the link P1-A, as indicated by vector VA.
The same applies to link P2-B: point P2 is the instant center of rotation for this link and point B moves in the direction as indicated by vector VB.
For determining the instant center of rotation of the third element of the linkage, the body BAC, the two points A and B are used because its moving characteristics are known, as derived from the information about the links P1-A and P2-B.
The direction of speed of point A is indicated by vector VA. Its instant center of rotation must be perpendicular to this vector (as VA is tangentially located on the circumference of a circle). The only line that fills the requirement is a line colinear with link P1-A. Somewhere on this line there is a point P, the instant center of rotation for the body BAC.
What applies to point A also applies to point B, therefore this instant center of rotation P is located on a line perpendicular to vector VB, a line colinear with link P2-B. Therefore, the instant center of rotation P of body BAC is the point where the lines through P1-A and P2-B cross.
Since this instant center of rotation P is the center for all points on the body BAC for any random point, say point C, the speed and direction of movement may be determined: connect P to C. The direction of movement of point C is perpendicular to this connection. The speed is proportional to the distance to point P.
Continuing this approach with the two links P1-A and P2-B rotating around their own instant centers of rotation the centrode for instant center of rotation P may be determined. From this the path of movement for C or any other point on body BAC may be determined.
Examples of application
In biomechanical research the instant center of rotation is observed for the functioning of the joints in the upper and lower extremities. For example, in analysing theknee
In humans and other primates, the knee joins the thigh with the leg and consists of two joints: one between the femur and tibia (tibiofemoral joint), and one between the femur and patella (patellofemoral joint). It is the largest joint in the hu ...
,
ankle
The ankle, the talocrural region or the jumping bone (informal) is the area where the foot and the leg meet. The ankle includes three joints: the ankle joint proper or talocrural joint, the subtalar joint, and the inferior tibiofibular joint. The ...
, or shoulder
The human shoulder is made up of three bones: the clavicle (collarbone), the scapula (shoulder blade), and the humerus (upper arm bone) as well as associated muscles, ligaments and tendons.
The articulations between the bones of the shoulder m ...
joints.
Such knowledge assists in developing artificial joint
Joint replacement is a procedure of orthopedic surgery known also as arthroplasty, in which an arthritic or dysfunctional joint surface is replaced with an orthopedic prosthesis. Joint replacement is considered as a treatment when severe joint pai ...
s and prosthesis
In medicine, a prosthesis (: prostheses; from ), or a prosthetic implant, is an artificial device that replaces a missing body part, which may be lost through physical trauma, disease, or a condition present at birth (Congenital, congenital disord ...
, such as elbow or finger joints.
Study of the joints of horses: "...velocity vectors determined from the instant centers of rotation indicated that the joint surfaces slide on each other."
Studies on turning a vessel moving through water.
The braking
A brake is a mechanical device that inhibits motion by absorbing energy from a moving system. It is used for slowing or stopping a moving vehicle, wheel, axle, or to prevent its motion, most often accomplished by means of friction.
Background
...
characteristics of a car may be improved by varying the design of a brake pedal mechanism.
Designing the suspension of a bicycle, or of a car.
In the case of the coupler link in a four-bar linkage
In the study of Mechanism (engineering), mechanisms, a four-bar linkage, also called a four-bar, is the simplest closed-Kinematic chain, chain movable linkage (mechanical), linkage. It consists of four Rigid body, bodies, called ''bars'' or ''link ...
, such as a double wishbone suspension in front view, the perpendiculars to the velocity lie along the links joining the grounded link to the coupler link. This construction is used to establish the kinematic
In physics, kinematics studies the geometrical aspects of motion of physical objects independent of forces that set them in motion. Constrained motion such as linked machine parts are also described as kinematics.
Kinematics is concerned with s ...
roll center
The roll center of a vehicle is the notional point at which the cornering forces in the suspension are reacted to the vehicle body.
There are two definitions of roll center. The most commonly used is the geometric (or kinematic) roll center, whe ...
of the suspension.
See also
*Angular velocity
In physics, angular velocity (symbol or \vec, the lowercase Greek letter omega), also known as the angular frequency vector,(UP1) is a pseudovector representation of how the angular position or orientation of an object changes with time, i ...
* Burmester's theory
In kinematics, Burmester theory comprises geometric techniques for synthesis of linkages. It was introduced in the late 19th century by Ludwig Burmester (1840–1927). His approach was to compute the geometric constraints of the linkage directly ...
* Centrode
* Point reflection group
* Rigid body
In physics, a rigid body, also known as a rigid object, is a solid body in which deformation is zero or negligible, when a deforming pressure or deforming force is applied on it. The distance between any two given points on a rigid body rema ...
* Roll center
The roll center of a vehicle is the notional point at which the cornering forces in the suspension are reacted to the vehicle body.
There are two definitions of roll center. The most commonly used is the geometric (or kinematic) roll center, whe ...
* Rotation around a fixed axis
Rotation around a fixed axis or axial rotation is a special case of rotational motion around an ''axis of rotation'' fixed, stationary, or static in three-dimensional space. This type of motion excludes the possibility of the instantaneous axis ...
* Screw axis
A screw axis (helical axis or twist axis) is a line that is simultaneously the axis of rotation and the line along which translation of a body occurs. Chasles' theorem shows that each Euclidean displacement in three-dimensional space has a screw ...
* Two-dimensional rotation
In Euclidean geometry, two-dimensional rotations and reflections are two kinds of Euclidean plane isometries which are related to one another.
Process
A rotation in the plane can be formed by composing a pair of reflections. First reflect a p ...
References
{{DEFAULTSORT:Instant centre Of Rotation Classical mechanics Kinematics Rotation Geometric centers