heat capacity

Heat capacity or thermal capacity is a physical property of matter, defined as the amount of heat to be supplied to an object to produce a unit change in its temperature. The SI unit of heat capacity is joule per kelvin (J/K).

Heat capacity is an extensive property. The corresponding intensive property is the specific heat capacity, found by dividing the heat capacity of an object by its mass. Dividing the heat capacity by the amount of substance in moles yields its molar heat capacity. The volumetric heat capacity measures the heat capacity per volume. In architecture and civil engineering, the heat capacity of a building is often referred to as its thermal mass.

Definition

Basic definition

The heat capacity of an object, denoted by $C$, is the limit
: $C = \lim_\frac,$
where $\Delta Q$ is the amount of heat that must be added to the object (of mass ''M'') in order to raise its temperature by $\Delta T$.

The value of this parameter usually varies considerably depending on the starting temperature $T$ of the object and the pressure $P$ applied to it. In particular, it typically varies dramatically with phase transitions such as melting or vaporization (see enthalpy of fusion and enthalpy of vaporization). Therefore, it should be considered a function $C(P,T)$ of those two variables.

Variation with temperature

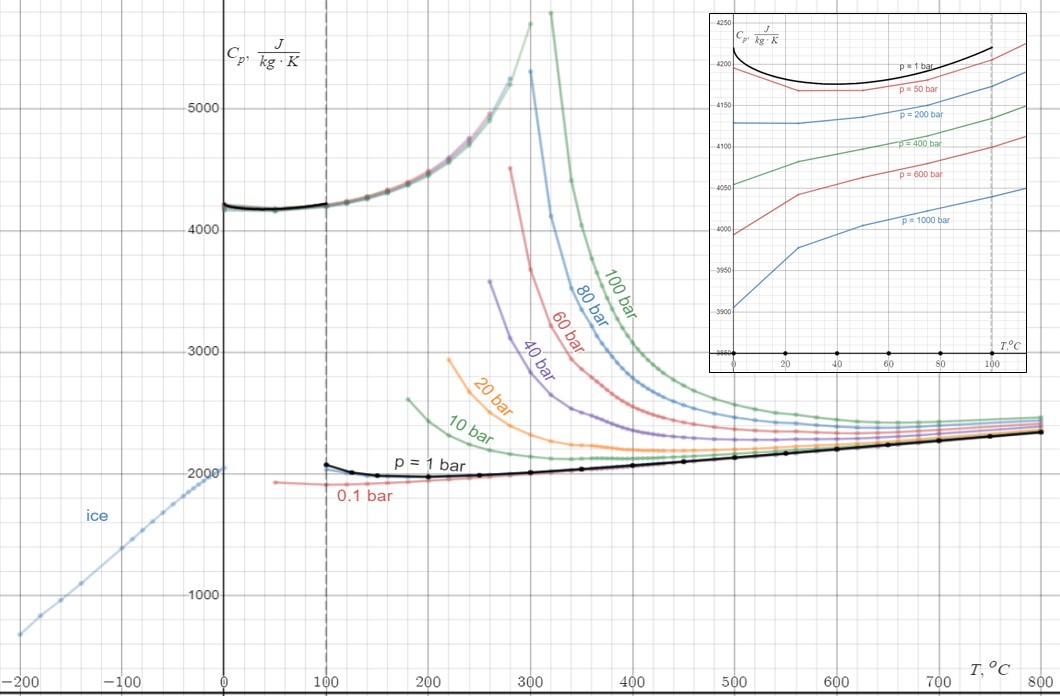
The variation can be ignored in contexts when working with objects in narrow ranges of temperature and pressure. For example, the heat capacity of a block of iron weighing one pound is about 204 J/K when measured from a starting temperature ''T'' = 25 °C and ''P'' = 1 atm of pressure. That approximate value is adequate for temperatures between 15 °C and 35 °C, and surrounding pressures from 0 to 10 atmospheres, because the exact value varies very little in those ranges. One can trust that the same heat input of 204 J will raise the temperature of the block from 15 °C to 16 °C, or from 34 °C to 35 °C, with negligible error.

Heat capacities of a homogeneous system undergoing different thermodynamic processes

At constant pressure, ''δQ'' = ''dU'' + ''PdV'' (

isobaric process)

At constant pressure, heat supplied to the system contributes to both the work done and the change in internal energy, according to the first law of thermodynamics. The heat capacity is called $C_P.$

At constant volume, ''dV'' = 0, ''δQ'' = ''dU'' (

isochoric process)

A system undergoing a process at constant volume implies that no expansion work is done, so the heat supplied contributes only to the change in internal energy. The heat capacity obtained this way is denoted $C_V.$ The value of $C_V$ is always less than the value of $C_P.$ ($C_V$ < $C_P.$)

Calculating ''C_P'' and ''C_V'' for an ideal gas

Mayer's relation:

: $C_P - C_V = nR.$

: $C_P/C_V = \gamma,$

where

: $n$ is the number of moles of the gas,
: $R$ is the universal gas constant,
: $\gamma$ is the heat capacity ratio (which can be calculated by knowing the number of degrees of freedom of the gas molecule).

Using the above two relations, the specific heats can be deduced as follows:

: $C_V = \frac,$

: $C_P = \gamma \frac.$

At constant temperature ( Isothermal process)

No change in internal energy (as the temperature of the system is constant throughout the process) leads to only work done by the total supplied heat, and thus an infinite amount of heat is required to increase the temperature of the system by a unit temperature, leading to infinite or undefined heat capacity of the system.

At the time of phase change (

Phase transition)

Heat capacity of a system undergoing phase transition is infinite, because the heat is utilized in changing the state of the material rather than raising the overall temperature.

Heterogeneous objects

The heat capacity may be well-defined even for heterogeneous objects, with separate parts made of different materials; such as an electric motor, a crucible with some metal, or a whole building. In many cases, the (isobaric) heat capacity of such objects can be computed by simply adding together the (isobaric) heat capacities of the individual parts.

However, this computation is valid only when all parts of the object are at the same external pressure before and after the measurement. That may not be possible in some cases. For example, when heating an amount of gas in an elastic container, its volume ''and pressure'' will both increase, even if the atmospheric pressure outside the container is kept constant. Therefore, the effective heat capacity of the gas, in that situation, will have a value intermediate between its isobaric and isochoric capacities $C_\mathrm$ and $C_\mathrm$.

For complex thermodynamic systems with several interacting parts and state variables, or for measurement conditions that are neither constant pressure nor constant volume, or for situations where the temperature is significantly non-uniform, the simple definitions of heat capacity above are not useful or even meaningful. The heat energy that is supplied may end up as kinetic energy (energy of motion) and potential energy (energy stored in force fields), both at macroscopic and atomic scales. Then the change in temperature will depends on the particular path that the system followed through its phase space between the initial and final states. Namely, one must somehow specify how the positions, velocities, pressures, volumes, etc. changed between the initial and final states; and use the general tools of thermodynamics to predict the system's reaction to a small energy input. The "constant volume" and "constant pressure" heating modes are just two among infinitely many paths that a simple homogeneous system can follow.

Measurement

The heat capacity can usually be measured by the method implied by its definition: start with the object at a known uniform temperature, add a known amount of heat energy to it, wait for its temperature to become uniform, and measure the change in its temperature. This method can give moderately accurate values for many solids; however, it cannot provide very precise measurements, especially for gases.

Units

International system

The SI unit for heat capacity of an object is joule per kelvin (J/K or J⋅K⁻¹). Since an increment of temperature of one degree Celsius is the same as an increment of one kelvin, that is the same unit as J/°C.

The heat capacity of an object is an amount of energy divided by a temperature change, which has the dimension L²⋅M⋅T⁻²⋅Θ⁻¹. Therefore, the SI unit J/K is equivalent to kilogram meter squared per second squared per kelvin (kg⋅m²⋅s⁻²⋅K⁻¹ ).

English (Imperial) engineering units

Professionals in construction, civil engineering, chemical engineering, and other technical disciplines, especially in the United States, may use the so-called English Engineering units, that include the pound (lb = 0.45359237 kg) as the unit of mass, the degree Fahrenheit or Rankine (°K, about 0.55556 °K) as the unit of temperature increment, and the British thermal unit (BTU ≈ 1055.06 J),
Published under the auspices of the ''Verein Deutscher Ingenieure'' (VDI).
as the unit of heat. In those contexts, the unit of heat capacity is 1 BTU/°R ≈ 1900 J/°K. The BTU was in fact defined so that the average heat capacity of one pound of water would be 1 BTU/°F. In this regard, with respect to mass, note conversion of 1 Btu/lb⋅°R ≈ 4,187 J/kg⋅°K and the calorie (below).

Calories

In chemistry, heat amounts are often measured in calories. Confusingly, two units with that name, denoted "cal" or "Cal", have been commonly used to measure amounts of heat:
* The "small calorie" (or "gram-calorie", "cal") is 4.184 J, exactly. It was originally defined so that the heat capacity of 1 gram of liquid water would be 1 cal/°C.
* The "grand calorie" (also "kilocalorie", "kilogram-calorie", or "food calorie"; "kcal" or "Cal") is 1000 cal, that is, 4184 J, exactly. It was originally defined so that the heat capacity of 1 kg of water would be 1 kcal/°C.
With these units of heat energy, the units of heat capacity are
:: 1 cal/°C = 4.184 J/K
:: 1 kcal/°C = 4184 J/K

Physical basis

Negative heat capacity

Most physical systems exhibit a positive heat capacity; constant-volume and constant-pressure heat capacities, rigorously defined as partial derivatives, are always positive for homogeneous bodies.Landau, L. D.; Lifshitz, E. M. (reprinted 2011). ''Statistical Physics Part 1'', Ch.II §21, 3rd edition, Elsevier ISBN 978-0-7506-3372-7 However, even though it can seem paradoxical at first, there are some systems for which the heat capacity $Q$/$\Delta T$ is ''negative''. Examples include a reversibly and nearly adiabatically expanding ideal gas, which cools, $\Delta T$< 0, while a small amount of heat $Q$ > 0 is put in, or combusting methane with increasing temperature, $\Delta T$> 0, and giving off heat, $Q$ < 0. Others are inhomogeneous systems that do not meet the strict definition of thermodynamic equilibrium. They include gravitating objects such as stars and galaxies, and also some nano-scale clusters of a few tens of atoms close to a phase transition. A negative heat capacity can result in a negative temperature.

Stars and black holes

According to the virial theorem, for a self-gravitating body like a star or an interstellar gas cloud, the average potential energy ''U''_pot and the average kinetic energy ''U''_kin are locked together in the relation

:$U_\text = -2 U_\text.$

The total energy ''U'' (= ''U''_pot + ''U''_kin) therefore obeys

:$U = - U_\text.$

If the system loses energy, for example, by radiating energy into space, the average kinetic energy actually increases. If a temperature is defined by the average kinetic energy, then the system therefore can be said to have a negative heat capacity.See e.g., Section 4 and onwards.

A more extreme version of this occurs with black holes. According to black-hole thermodynamics, the more mass and energy a black hole absorbs, the colder it becomes. In contrast, if it is a net emitter of energy, through Hawking radiation, it will become hotter and hotter until it boils away.

Consequences

According to the Second Law of Thermodynamics, when two systems with different temperatures interact via a purely thermal connection, heat will flow from the hotter system to the cooler one (this can also be understood from a statistical point of view). Therefore, if such systems have equal temperatures, they are at thermal equilibrium. However, this equilibrium is stable only if the systems have ''positive'' heat capacities. For such systems, when heat flows from a higher temperature system to a lower temperature one, the temperature of the first decreases and that of the latter increases, so that both approach equilibrium. In contrast, for systems with ''negative'' heat capacities, the temperature of the hotter system will further increase as it loses heat, and that of the colder will further decrease, so that they will move farther from equilibrium. This means that the equilibrium is unstable.

For example, according to theory, the smaller (less massive) a black hole is, the smaller its Schwarzschild radius will be and therefore the greater the curvature of its event horizon will be, as well as its temperature. Thus, the smaller the black hole, the more thermal radiation it will emit and the more quickly it will evaporate.

See also

* Quantum statistical mechanics
* Heat capacity ratio
* Statistical mechanics
* Thermodynamic equations
* Thermodynamic databases for pure substances
* Heat equation
* Heat transfer coefficient
* Heat of mixing
* Latent heat
* Material properties (thermodynamics)
* Joback method (estimation of heat capacities)
* Specific heat of melting (enthalpy of fusion)
* Specific heat of vaporization (enthalpy of vaporization)
* Volumetric heat capacity
* Thermal mass
* R-value (insulation)
* Storage heater
* Frenkel line
* Table of specific heat capacities

References

Further reading

* Encyclopædia Britannica, 2015,
Heat capacity (Alternate title: thermal capacity)
.

{{Authority control

Physical quantities
Thermodynamic properties