Hyperbolic Orthogonality on:
[Wikipedia]
[Google]
[Amazon]
 In
In
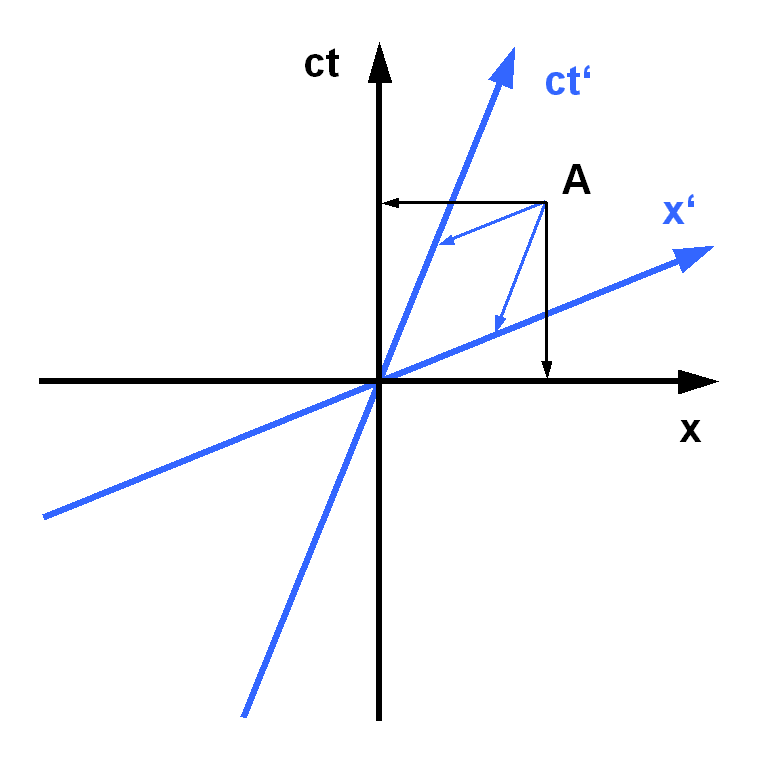 One of the premises of relativity is that the
One of the premises of relativity is that the
geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, the relation of hyperbolic orthogonality between two lines separated by the asymptotes of a hyperbola is a concept used in special relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory of the relationship between Spacetime, space and time. In Albert Einstein's 1905 paper, Annus Mirabilis papers#Special relativity,
"On the Ele ...
to define simultaneous events. Two events will be simultaneous when they are on a line hyperbolically orthogonal to a particular timeline. This dependence on a certain timeline is determined by velocity, and is the basis for the relativity of simultaneity. Furthermore, keeping time and space axes hyperbolically orthogonal, as in Minkowski space, gives a constant result when measurements are taken of the speed of light.
Geometry
Two lines are hyperbolic orthogonal when they are reflections of each other over the asymptote of a given hyperbola. Two particular hyperbolas are frequently used in the plane: The relation of hyperbolic orthogonality actually applies to classes of parallel lines in the plane, where any particular line can represent the class. Thus, for a given hyperbola and asymptote ''A'', a pair of lines (''a'', ''b'') are hyperbolic orthogonal if there is a pair (''c'', ''d'') such that , and ''c'' is the reflection of ''d'' across ''A''. Similar to the perpendularity of a circle radius to thetangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points o ...
, a radius to a hyperbola is hyperbolic orthogonal to a tangent to the hyperbola.
A bilinear form
In mathematics, a bilinear form is a bilinear map on a vector space (the elements of which are called '' vectors'') over a field ''K'' (the elements of which are called '' scalars''). In other words, a bilinear form is a function that is linea ...
is used to describe orthogonality in analytic geometry, with two elements orthogonal when their bilinear form vanishes. In the plane of complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s , the bilinear form is , while in the plane of hyperbolic numbers the bilinear form is
:The vectors ''z''1 and ''z''2 in the complex number plane, and ''w''1 and ''w''2 in the hyperbolic number plane are said to be respectively ''Euclidean orthogonal'' or ''hyperbolic orthogonal'' if their respective inner products ilinear formsare zero.
The bilinear form may be computed as the real part of the complex product of one number with the conjugate of the other. Then
: entails perpendicularity in the complex plane, while
: implies the ''ws are hyperbolic orthogonal.
The notion of hyperbolic orthogonality arose in analytic geometry
In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.
Analytic geometry is used in physics and engineering, and als ...
in consideration of conjugate diameters
In geometry, two diameters of a conic section are said to be conjugate if each chord (geometry), chord parallel (geometry), parallel to one diameter is bisection, bisected by the other diameter. For example, two diameters of a circle are conjugate ...
of ellipses and hyperbolas. If ''g'' and ''g''′ represent the slopes of the conjugate diameters, then in the case of an ellipse and in the case of a hyperbola. When ''a'' = ''b'' the ellipse is a circle and the conjugate diameters are perpendicular while the hyperbola is rectangular and the conjugate diameters are hyperbolic-orthogonal.
In the terminology of projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting (''p ...
, the operation of taking the hyperbolic orthogonal line is an involution. Suppose the slope of a vertical line is denoted ∞ so that all lines have a slope in the projectively extended real line. Then whichever hyperbola (A) or (B) is used, the operation is an example of a hyperbolic involution where the asymptote is invariant. Hyperbolically orthogonal lines lie in different sectors of the plane, determined by the asymptotes of the hyperbola, thus the relation of hyperbolic orthogonality is a heterogeneous relation
In mathematics, a binary relation associates some elements of one set called the ''domain'' with some elements of another set called the ''codomain''. Precisely, a binary relation over sets X and Y is a set of ordered pairs (x, y), where x i ...
on sets of lines in the plane.
Constant light speed
 One of the premises of relativity is that the
One of the premises of relativity is that the speed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant exactly equal to ). It is exact because, by international agreement, a metre is defined as the length of the path travelled by light in vacuum during a time i ...
does not depend on the inertial frame of reference
In classical physics and special relativity, an inertial frame of reference (also called an inertial space or a Galilean reference frame) is a frame of reference in which objects exhibit inertia: they remain at rest or in uniform motion relative ...
in which the measurements are done. This premise has been associated with null results in the Michaelson–Morley experiment. As long as space and time axes are hyperbolically orthogonal, the measurement of the speed of light will give the same result. The seeming paradox of light speed invariance with respect to moving observers is resolved in special relativity by this feature of Minkowski space.
Simultaneity
Since Hermann Minkowski's foundation forspacetime
In physics, spacetime, also called the space-time continuum, is a mathematical model that fuses the three dimensions of space and the one dimension of time into a single four-dimensional continuum. Spacetime diagrams are useful in visualiz ...
study in 1908, the concept of points in a spacetime plane being hyperbolic-orthogonal to a timeline (tangent to a world line
The world line (or worldline) of an object is the path that an object traces in 4-dimensional spacetime. It is an important concept of modern physics, and particularly theoretical physics.
The concept of a "world line" is distinguished from c ...
) has been used to define simultaneity of events relative to the timeline, or relativity of simultaneity. In Minkowski's development the hyperbola of type (B) above is in use. Two vectors (, , , ) and (, , , ) are ''normal'' (meaning hyperbolic orthogonal) when
:
When = 1 and the s and s are zero, ≠ 0, ≠ 0, then .
Given a hyperbola with asymptote ''A'', its reflection in ''A'' produces the conjugate hyperbola. Any diameter of the original hyperbola is reflected to a conjugate diameter. The directions indicated by conjugate diameters are taken for space and time axes in relativity.
As E. T. Whittaker wrote in 1910, " hehyperbola is unaltered when any pair of conjugate diameters are taken as new axes, and a new unit of length is taken proportional to the length of either of these diameters." E. T. Whittaker (1910) A History of the Theories of Aether and Electricity Dublin: Longmans, Green and Co. (see page 441) On this principle of relativity
In physics, the principle of relativity is the requirement that the equations describing the laws of physics have the same form in all admissible frames of reference.
For example, in the framework of special relativity, the Maxwell equations ...
, he then wrote the Lorentz transformation in the modern form using rapidity
In special relativity, the classical concept of velocity is converted to rapidity to accommodate the limit determined by the speed of light. Velocities must be combined by Einstein's velocity-addition formula. For low speeds, rapidity and velo ...
.
Edwin Bidwell Wilson and Gilbert N. Lewis developed the concept within synthetic geometry
Synthetic geometry (sometimes referred to as axiomatic geometry or even pure geometry) is geometry without the use of coordinates. It relies on the axiomatic method for proving all results from a few basic properties initially called postulates ...
in 1912. They note "in our plane no pair of perpendicular yperbolic-orthogonallines is better suited to serve as coordinate axes than any other pair"Edwin B. Wilson & Gilbert N. Lewis (1912) "The Space-time Manifold of Relativity. The Non-Euclidean Geometry of Mechanics and Electromagnetics" Proceedings of the American Academy of Arts and Sciences
The American Academy of Arts and Sciences (The Academy) is one of the oldest learned societies in the United States. It was founded in 1780 during the American Revolution by John Adams, John Hancock, James Bowdoin, Andrew Oliver, and other ...
48:387–507, esp. 415
References
* G. D. Birkhoff (1923) ''Relativity and Modern Physics'', pages 62,3,Harvard University Press
Harvard University Press (HUP) is an academic publishing house established on January 13, 1913, as a division of Harvard University. It is a member of the Association of University Presses. Its director since 2017 is George Andreou.
The pres ...
.
* Francesco Catoni, Dino Boccaletti, & Roberto Cannata (2008) ''Mathematics of Minkowski Space'', Birkhäuser Verlag, Basel. See page 38, Pseudo-orthogonality.
* Robert Goldblatt (1987) ''Orthogonality and Spacetime Geometry'', chapter 1: A Trip on Einstein's Train, Universitext Springer-Verlag
*
{{Relativity
Minkowski spacetime
Angle