Hydrological model on:
[Wikipedia]
[Google]
[Amazon]
A hydrologic model is a simplification of a real-world system (e.g., surface water, soil water, wetland, groundwater, estuary) that aids in understanding, predicting, and managing water resources. Both the flow and quality of water are commonly studied using hydrologic models.

 Scale models offer a useful approximation of physical or chemical processes at a size that allows for greater ease of visualization. The model may be created in one (core, column), two (plan, profile), or three dimensions, and can be designed to represent a variety of specific initial and boundary conditions as needed to answer a question.
Scale models commonly use physical properties that are similar to their natural counterparts (e.g., gravity, temperature). Yet, maintaining some properties at their natural values can lead to erroneous predictions. Properties such as viscosity, friction, and surface area must be adjusted to maintain appropriate flow and transport behavior. This usually involves matching dimensionless ratios (e.g.,
Scale models offer a useful approximation of physical or chemical processes at a size that allows for greater ease of visualization. The model may be created in one (core, column), two (plan, profile), or three dimensions, and can be designed to represent a variety of specific initial and boundary conditions as needed to answer a question.
Scale models commonly use physical properties that are similar to their natural counterparts (e.g., gravity, temperature). Yet, maintaining some properties at their natural values can lead to erroneous predictions. Properties such as viscosity, friction, and surface area must be adjusted to maintain appropriate flow and transport behavior. This usually involves matching dimensionless ratios (e.g.,  Groundwater flow can be visualized using a scale model built of acrylic and filled with sand, silt, and clay. Water and tracer dye may be pumped through this system to represent the flow of the simulated groundwater. Some physical aquifer models are between two and three dimensions, with simplified boundary conditions simulated using pumps and barriers.
Groundwater flow can be visualized using a scale model built of acrylic and filled with sand, silt, and clay. Water and tracer dye may be pumped through this system to represent the flow of the simulated groundwater. Some physical aquifer models are between two and three dimensions, with simplified boundary conditions simulated using pumps and barriers.

 :
:
 Example 2
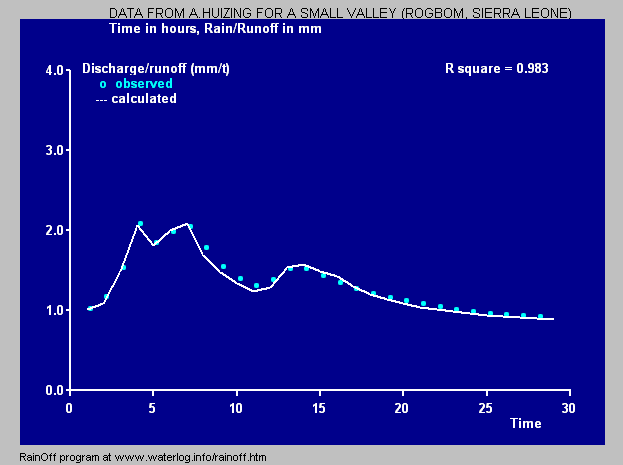
Instead of using a series of linear reservoirs, also the model of a non-linear reservoir can be used.
In such a model the constant K in the above equation, that may also be called ''reaction factor'', needs to be replaced by another symbol, say α (Alpha), to indicate the dependence of this factor on storage (S) and discharge (q).
In the left figure the relation is quadratic:
:α = 0.0123 q2 + 0.138 q - 0.112
Example 2
Instead of using a series of linear reservoirs, also the model of a non-linear reservoir can be used.
In such a model the constant K in the above equation, that may also be called ''reaction factor'', needs to be replaced by another symbol, say α (Alpha), to indicate the dependence of this factor on storage (S) and discharge (q).
In the left figure the relation is quadratic:
:α = 0.0123 q2 + 0.138 q - 0.112
PORFLOW
MIKE SHE, and WEAP.
 Physical models use
Physical models use

Analog models
Prior to the advent of computer models, hydrologic modeling used analog models to simulate flow and transport systems. Unlikemathematical models
A mathematical model is an abstract description of a concrete system using mathematical concepts and language. The process of developing a mathematical model is termed ''mathematical modeling''. Mathematical models are used in applied mathemati ...
that use equations to describe, predict, and manage hydrologic systems, analog models use non-mathematical approaches to simulate hydrology.
Two general categories of analog models are common; scale analogs that use miniaturized versions of the physical system and process analogs that use comparable physics (e.g., electricity, heat, diffusion) to mimic the system of interest.
Scale analogs
 Scale models offer a useful approximation of physical or chemical processes at a size that allows for greater ease of visualization. The model may be created in one (core, column), two (plan, profile), or three dimensions, and can be designed to represent a variety of specific initial and boundary conditions as needed to answer a question.
Scale models commonly use physical properties that are similar to their natural counterparts (e.g., gravity, temperature). Yet, maintaining some properties at their natural values can lead to erroneous predictions. Properties such as viscosity, friction, and surface area must be adjusted to maintain appropriate flow and transport behavior. This usually involves matching dimensionless ratios (e.g.,
Scale models offer a useful approximation of physical or chemical processes at a size that allows for greater ease of visualization. The model may be created in one (core, column), two (plan, profile), or three dimensions, and can be designed to represent a variety of specific initial and boundary conditions as needed to answer a question.
Scale models commonly use physical properties that are similar to their natural counterparts (e.g., gravity, temperature). Yet, maintaining some properties at their natural values can lead to erroneous predictions. Properties such as viscosity, friction, and surface area must be adjusted to maintain appropriate flow and transport behavior. This usually involves matching dimensionless ratios (e.g., Reynolds number
In fluid dynamics, the Reynolds number () is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between Inertia, inertial and viscous forces. At low Reynolds numbers, flows tend to ...
, Froude number
In continuum mechanics, the Froude number (, after William Froude, ) is a dimensionless number defined as the ratio of the flow inertia to the external force field (the latter in many applications simply due to gravity). The Froude number is ba ...
).
 Groundwater flow can be visualized using a scale model built of acrylic and filled with sand, silt, and clay. Water and tracer dye may be pumped through this system to represent the flow of the simulated groundwater. Some physical aquifer models are between two and three dimensions, with simplified boundary conditions simulated using pumps and barriers.
Groundwater flow can be visualized using a scale model built of acrylic and filled with sand, silt, and clay. Water and tracer dye may be pumped through this system to represent the flow of the simulated groundwater. Some physical aquifer models are between two and three dimensions, with simplified boundary conditions simulated using pumps and barriers.
Process analogs
Process analogs are used in hydrology to represent fluid flow using the similarity between Darcy's law,Ohm's law
Ohm's law states that the electric current through a Electrical conductor, conductor between two Node (circuits), points is directly Proportionality (mathematics), proportional to the voltage across the two points. Introducing the constant of ...
, Fourier's law
Thermal conduction is the diffusion of thermal energy (heat) within one material or between materials in contact. The higher temperature object has molecules with more kinetic energy; collisions between molecules distributes this kinetic energy ...
, and Fick's law
Fick's laws of diffusion describe diffusion and were first posited by Adolf Fick in 1855 on the basis of largely experimental results. They can be used to solve for the diffusion coefficient, . Fick's first law can be used to derive his second ...
. The analogs to fluid flow are the flux
Flux describes any effect that appears to pass or travel (whether it actually moves or not) through a surface or substance. Flux is a concept in applied mathematics and vector calculus which has many applications in physics. For transport phe ...
of electricity
Electricity is the set of physical phenomena associated with the presence and motion of matter possessing an electric charge. Electricity is related to magnetism, both being part of the phenomenon of electromagnetism, as described by Maxwel ...
, heat
In thermodynamics, heat is energy in transfer between a thermodynamic system and its surroundings by such mechanisms as thermal conduction, electromagnetic radiation, and friction, which are microscopic in nature, involving sub-atomic, ato ...
, and solutes
In chemistry, a solution is defined by IUPAC as "A liquid or solid phase containing more than one substance, when for convenience one (or more) substance, which is called the solvent, is treated differently from the other substances, which are ...
, respectively. The corresponding analogs to fluid potential are voltage
Voltage, also known as (electrical) potential difference, electric pressure, or electric tension, is the difference in electric potential between two points. In a Electrostatics, static electric field, it corresponds to the Work (electrical), ...
, temperature
Temperature is a physical quantity that quantitatively expresses the attribute of hotness or coldness. Temperature is measurement, measured with a thermometer. It reflects the average kinetic energy of the vibrating and colliding atoms making ...
, and solute concentration
In chemistry, concentration is the abundance of a constituent divided by the total volume of a mixture. Several types of mathematical description can be distinguished: '' mass concentration'', '' molar concentration'', '' number concentration'', ...
(or chemical potential
In thermodynamics, the chemical potential of a Chemical specie, species is the energy that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition. The chemical potent ...
). The analogs to hydraulic conductivity
In science and engineering, hydraulic conductivity (, in SI units of meters per second), is a property of porous materials, soils and Rock (geology), rocks, that describes the ease with which a fluid (usually water) can move through the porosity, ...
are electrical conductivity
Electrical resistivity (also called volume resistivity or specific electrical resistance) is a fundamental specific property of a material that measures its electrical resistance or how strongly it resists electric current. A low resistivity in ...
, thermal conductivity
The thermal conductivity of a material is a measure of its ability to heat conduction, conduct heat. It is commonly denoted by k, \lambda, or \kappa and is measured in W·m−1·K−1.
Heat transfer occurs at a lower rate in materials of low ...
, and the solute diffusion coefficient
Diffusivity, mass diffusivity or diffusion coefficient is usually written as the proportionality constant between the molar flux due to molecular diffusion and the negative value of the gradient in the concentration of the species. More accurate ...
.
An early process analog model was an electrical network model of an aquifer composed of resistors in a grid. Voltages were assigned along the outer boundary, and then measured within the domain. Electrical conductivity paper can also be used instead of resistors.
Statistical models
Statistical models
A statistical model is a mathematical model that embodies a set of statistical assumptions concerning the generation of sample data (and similar data from a larger population). A statistical model represents, often in considerably idealized form ...
are a type of mathematical model
A mathematical model is an abstract and concrete, abstract description of a concrete system using mathematics, mathematical concepts and language of mathematics, language. The process of developing a mathematical model is termed ''mathematical m ...
that are commonly used in hydrology to describe data, as well as relationships between data. Using statistical methods, hydrologists develop empirical relationship
In science
Science is a systematic discipline that builds and organises knowledge in the form of testable hypotheses and predictions about the universe. Modern science is typically divided into twoor threemajor branches: the natural science ...
s between observed variables, find trends in historical data, or forecast probable storm or drought events.
Moments
Statistical moments (e.g.,mean
A mean is a quantity representing the "center" of a collection of numbers and is intermediate to the extreme values of the set of numbers. There are several kinds of means (or "measures of central tendency") in mathematics, especially in statist ...
, standard deviation
In statistics, the standard deviation is a measure of the amount of variation of the values of a variable about its Expected value, mean. A low standard Deviation (statistics), deviation indicates that the values tend to be close to the mean ( ...
, skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined.
For a unimodal ...
, kurtosis
In probability theory and statistics, kurtosis (from , ''kyrtos'' or ''kurtos'', meaning "curved, arching") refers to the degree of “tailedness” in the probability distribution of a real-valued random variable. Similar to skewness, kurtos ...
) are used to describe the information content of data. These moments can then be used to determine an appropriate frequency distribution Distribution may refer to:
Mathematics
*Distribution (mathematics), generalized functions used to formulate solutions of partial differential equations
*Probability distribution, the probability of a particular value or value range of a varia ...
, which can then be used as a probability model. Two common techniques include L-moment ratios and Moment-Ratio Diagrams.
The frequency of extremal events, such as severe droughts and storms, often requires the use of distributions that focus on the tail of the distribution, rather than the data nearest the mean. These techniques, collectively known as extreme value analysis, provide a methodology for identifying the likelihood and uncertainty of extreme events. Examples of extreme value distributions include the Gumbel, Pearson, and generalized extreme value. The standard method for determining peak discharge uses the log-Pearson Type III (log-gamma) distribution and observed annual flow peaks.
Correlation analysis
The degree and nature of correlation may be quantified, by using a method such as thePearson correlation coefficient
In statistics, the Pearson correlation coefficient (PCC) is a correlation coefficient that measures linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviatio ...
, autocorrelation
Autocorrelation, sometimes known as serial correlation in the discrete time case, measures the correlation of a signal with a delayed copy of itself. Essentially, it quantifies the similarity between observations of a random variable at differe ...
, or the T-test
Student's ''t''-test is a statistical test used to test whether the difference between the response of two groups is Statistical significance, statistically significant or not. It is any statistical hypothesis testing, statistical hypothesis test ...
. The degree of randomness or uncertainty in the model may also be estimated using stochastic Stochastic (; ) is the property of being well-described by a random probability distribution. ''Stochasticity'' and ''randomness'' are technically distinct concepts: the former refers to a modeling approach, while the latter describes phenomena; i ...
s, or residual analysis. These techniques may be used in the identification of flood dynamics, storm characterization, and groundwater flow in karst systems.
Regression analysis is used in hydrology to determine whether a relationship may exist between independent and dependent variables. Bivariate diagrams are the most commonly used statistical regression model in the physical sciences, but there are a variety of models available from simplistic to complex. In a bivariate diagram, a linear
In mathematics, the term ''linear'' is used in two distinct senses for two different properties:
* linearity of a '' function'' (or '' mapping'');
* linearity of a '' polynomial''.
An example of a linear function is the function defined by f(x) ...
or higher-order model may be fitted to the data.
Factor analysis
Factor analysis is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved variables called factors. For example, it is possible that variations in six observe ...
and principal component analysis
Principal component analysis (PCA) is a linear dimensionality reduction technique with applications in exploratory data analysis, visualization and data preprocessing.
The data is linearly transformed onto a new coordinate system such that th ...
are multivariate statistical procedures used to identify relationships between hydrologic variables.
Convolution
In mathematics (in particular, functional analysis), convolution is a operation (mathematics), mathematical operation on two function (mathematics), functions f and g that produces a third function f*g, as the integral of the product of the two ...
is a mathematical operation on two different functions to produce a third function. With respect to hydrologic modeling, convolution can be used to analyze stream discharge's relationship to precipitation. Convolution is used to predict discharge downstream after a precipitation event. This type of model would be considered a “lag convolution”, because of the predicting of the “lag time” as water moves through the watershed using this method of modeling.
Time-series
In mathematics, a time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. E ...
analysis is used to characterize temporal correlation within a data series as well as between different time series. Many hydrologic phenomena are studied within the context of historical probability. Within a temporal dataset, event frequencies, trends, and comparisons may be made by using the statistical techniques of time series analysis. The questions that are answered through these techniques are often important for municipal planning, civil engineering, and risk assessments.
Markov chains
In probability theory and statistics, a Markov chain or Markov process is a stochastic process describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally, ...
are a mathematical technique for determine the probability of a state or event based on a previous state or event. The event must be dependent, such as rainy weather. Markov Chains were first used to model rainfall event length in days in 1976, and continues to be used for flood risk assessment and dam management.
Data-driven models
Data-driven model
Data-driven models are a class of computational models that primarily rely on historical data collected throughout a system's or process' lifetime to establish relationships between input, internal, and output variables. Commonly found in numerou ...
s in hydrology emerged as an alternative approach to traditional statistical models, offering a more flexible and adaptable methodology for analysing and predicting various aspects of hydrological processes. While statistical models rely on rigorous assumptions about probability distributions, data-driven models leverage techniques from artificial intelligence, machine learning, and statistical analysis, including correlation analysis, time series analysis, and statistical moments, to learn complex patterns and dependencies from historical data. This allows them to make more accurate predictions and provide insights into the underlying processes.
Since their inception in the latter half of the 20th century, data-driven models have gained popularity in the water domain, as they help improve forecasting, decision-making, and management of water resources. A couple of notable publications that use data-driven models in hydrology include "Application of machine learning techniques for rainfall-runoff modelling" by Solomatine and Siek (2004), and "Data-driven modelling approaches for hydrological forecasting and prediction" by Valipour et al. (2021). These models are commonly used for predicting rainfall, runoff, groundwater levels, and water quality, and have proven to be valuable tools for optimizing water resource management strategies.
Conceptual models

Conceptual model
The term conceptual model refers to any model that is formed after a wikt:concept#Noun, conceptualization or generalization process. Conceptual models are often abstractions of things in the real world, whether physical or social. Semantics, Semant ...
s represent hydrologic systems using physical concepts. The conceptual model is used as the starting point for defining the important model components. The relationships between model components are then specified using algebraic equations
In mathematics, an algebraic equation or polynomial equation is an equation of the form P = 0, where ''P'' is a polynomial with coefficients in some field, often the field of the rational numbers.
For example, x^5-3x+1=0 is an algebraic equation ...
, ordinary or partial differential equations
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives.
The function is often thought of as an "unknown" that solves the equation, similar to how ...
, or integral equations
In mathematical analysis, integral equations are equations in which an unknown Function (mathematics), function appears under an integral sign. In mathematical notation, integral equations may thus be expressed as being of the form: f(x_1,x_2,x_3 ...
. The model is then solved using analytical or numerical procedures.
Conceptual models are commonly used to represent the important components (e.g., features, events, and processes) that relate hydrologic inputs to outputs. These components describe the important functions of the system
A system is a group of interacting or interrelated elements that act according to a set of rules to form a unified whole. A system, surrounded and influenced by its open system (systems theory), environment, is described by its boundaries, str ...
of interest, and are often constructed using entities (stores of water) and relationships between these entitites (flows or fluxes between stores). The conceptual model is coupled with scenarios to describe specific events (either input or outcome scenarios).
For example, a watershed model could be represented using tributaries
A tributary, or an ''affluent'', is a stream or river that flows into a larger stream ('' main stem'' or ''"parent"''), river, or a lake. A tributary does not flow directly into a sea or ocean. Tributaries, and the main stem river into which the ...
as boxes with arrows pointing toward a box that represents the main river. The conceptual model would then specify the important watershed features (e.g., land use, land cover, soils, subsoil
Subsoil is the layer of soil under the topsoil on the surface of the ground. Like topsoil, it is composed of a variable mixture of small particles such as sand, silt and clay, but with a much lower percentage of organic matter and humus. The su ...
s, geology, wetlands, lakes), atmospheric exchanges (e.g., precipitation, evapotranspiration), human uses (e.g., agricultural, municipal, industrial, navigation, thermo- and hydro-electric power generation), flow processes (e.g., overland, interflow, baseflow, channel flow), transport processes (e.g.,
sediments, nutrients, pathogens), and events (e.g., low-, flood-, and mean-flow conditions).
Model scope and complexity is dependent on modeling objectives, with greater detail required if human or environmental systems are subject to greater risk. Systems modeling
A system is a group of interacting or interrelated elements that act according to a set of rules to form a unified whole. A system, surrounded and influenced by its environment, is described by its boundaries, structure and purpose and is exp ...
can be used for building conceptual models that are then populated using mathematical relationships.
Example 1
The linear-reservoir model (or Nash model) is widely used for rainfall-runoff analysis. The model uses a cascade of linear reservoirs along with a constant first-order storage coefficient, ''K'', to predict the outflow from each reservoir (which is then used as the input to the next in the series).
The model combines continuity and storage-discharge equations, which yields an ordinary differential equation that describes outflow from each reservoir. The continuity equation for tank models is:
:
which indicates that the change in storage over time is the difference between inflows and outflows. The storage-discharge relationship is:
:
where K is a constant that indicates how quickly the reservoir drains; a smaller value indicates more rapid outflow. Combining these two equation yields
:
and has the solution:
 :
:
 Example 2
Instead of using a series of linear reservoirs, also the model of a non-linear reservoir can be used.
In such a model the constant K in the above equation, that may also be called ''reaction factor'', needs to be replaced by another symbol, say α (Alpha), to indicate the dependence of this factor on storage (S) and discharge (q).
In the left figure the relation is quadratic:
:α = 0.0123 q2 + 0.138 q - 0.112
Example 2
Instead of using a series of linear reservoirs, also the model of a non-linear reservoir can be used.
In such a model the constant K in the above equation, that may also be called ''reaction factor'', needs to be replaced by another symbol, say α (Alpha), to indicate the dependence of this factor on storage (S) and discharge (q).
In the left figure the relation is quadratic:
:α = 0.0123 q2 + 0.138 q - 0.112
Governing equations
Governing equation
The governing equations of a mathematical model describe how the values of the unknown variables (i.e. the dependent variables) change when one or more of the known (i.e. independent) variables change.
Physical systems can be modeled phenomenol ...
s are used to mathematically define the behavior of the system. Algebraic equations are likely often used for simple systems, while ordinary and partial differential equations are often used for problems that change in space in time. Examples of governing equations include:
Manning's equation is an algebraic equation that predicts stream velocity as a function of channel roughness, the hydraulic radius, and the channel slope:
:
Darcy's law describes steady, one-dimensional groundwater flow using the hydraulic conductivity and the hydraulic gradient:
:
Groundwater flow equation Used in hydrogeology, the groundwater flow equation is the mathematical relationship which is used to describe the flow of groundwater through an aquifer. The transient flow of groundwater is described by a form of the diffusion equation, similar ...
describes time-varying, multidimensional groundwater flow using the aquifer transmissivity and storativity:
:
Advection-Dispersion equation describes solute movement in steady, one-dimensional flow using the solute dispersion coefficient and the groundwater velocity:
:
Poiseuille's law describes laminar, steady, one-dimensional fluid flow using the shear stress
Shear stress (often denoted by , Greek alphabet, Greek: tau) is the component of stress (physics), stress coplanar with a material cross section. It arises from the shear force, the component of force vector parallel to the material cross secti ...
:
:
Cauchy's integral is an integral method for solving boundary value problems:
:
Solution algorithms
Analytic methods
Exact solutions for algebraic, differential, and integral equations can often be found using specified boundary conditions and simplifying assumptions.Laplace
Pierre-Simon, Marquis de Laplace (; ; 23 March 1749 – 5 March 1827) was a French polymath, a scholar whose work has been instrumental in the fields of physics, astronomy, mathematics, engineering, statistics, and philosophy. He summariz ...
and Fourier transform methods are widely used to find analytic solutions to differential and integral equations.
Numeric methods
Many real-world mathematical models are too complex to meet the simplifying assumptions required for an analytic solution. In these cases, the modeler develops a numerical solution that approximates the exact solution. Solution techniques include the finite-difference and finite-element methods, among many others. Specialized software may also be used to solve sets of equations using a graphical user interface and complex code, such that the solutions are obtained relatively rapidly and the program may be operated by a layperson or an end user without a deep knowledge of the system. There are model software packages for hundreds of hydrologic purposes, such as surface water flow, nutrient transport and fate, and groundwater flow. Commonly used numerical models includeSWAT
A SWAT (''Special Weapons and Tactics'') team is a generic term for a police tactical unit within the United States, though the term has also been used by other nations.
SWAT units are generally trained, equipped, and deployed to res ...
, MODFLOW, FEFLOWPORFLOW
MIKE SHE, and WEAP.
Model calibration and evaluation
 Physical models use
Physical models use parameters
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when ...
to characterize the unique aspects of the system being studied. These parameters can be obtained using laboratory and field studies, or estimated by finding the best correspondence between observed and modelled behavior. Between neighbouring catchments which have physical and hydrological similarities, the model parameters varies smoothly suggesting the spatial transferability of parameters.
Model evaluation
In common usage, evaluation is a systematic determination and assessment of a subject's merit, worth and significance, using criteria governed by a set of Standardization, standards. It can assist an organization, program, design, project or any o ...
is used to determine the ability of the calibrated model to meet the needs of the modeler. A commonly used measure of hydrologic model fit is the Nash-Sutcliffe efficiency coefficient.
See also
*Hydrological optimization Hydrological optimization applies mathematical optimization techniques (such as dynamic programming, linear programming, integer programming, or quadratic programming) to water-related problems. These problems may be for surface water, groundwate ...
*Scientific modelling
Scientific modelling is an activity that produces models representing empirical objects, phenomena, and physical processes, to make a particular part or feature of the world easier to understand, define, quantify, visualize, or simulate. It ...
* Soil and Water Assessment Tool
References
External links
* http://drought.unl.edu/MonitoringTools/DownloadableSPIProgram.aspx {{Computer modeling Water resources management