Hook Length Formula on:
[Wikipedia]
[Google]
[Amazon]
In combinatorial mathematics, the hook length formula is a formula for the number of
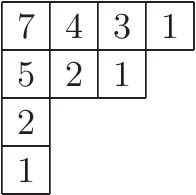 The figure on the right shows hook lengths for the cells in the
The figure on the right shows hook lengths for the cells in the
 where the sum runs over all Young diagrams obtained from by deleting one corner cell. (The maximal entry of the Young tableau of shape occurs at one of its corner cells, so deleting it gives a Young tableaux of shape .)
We define and , so it is enough to show the same recurrence
:
which would imply by induction. The above sum can be viewed as a sum of probabilities by writing it as
:
We therefore need to show that the numbers define a probability measure on the set of Young diagrams with . This is done in a constructive way by defining a random walk, called the hook walk, on the cells of the Young diagram , which eventually selects one of the corner cells of (which are in bijection with diagrams for which ). The hook walk is defined by the following rules.
# Pick a cell uniformly at random from cells. Start the random walk from there.
# Successor of current cell is chosen uniformly at random from the hook .
# Continue until you reach a corner cell .
Proposition: For a given corner cell of , we have
:
where .
Given this, summing over all corner cells gives as claimed.
where the sum runs over all Young diagrams obtained from by deleting one corner cell. (The maximal entry of the Young tableau of shape occurs at one of its corner cells, so deleting it gives a Young tableaux of shape .)
We define and , so it is enough to show the same recurrence
:
which would imply by induction. The above sum can be viewed as a sum of probabilities by writing it as
:
We therefore need to show that the numbers define a probability measure on the set of Young diagrams with . This is done in a constructive way by defining a random walk, called the hook walk, on the cells of the Young diagram , which eventually selects one of the corner cells of (which are in bijection with diagrams for which ). The hook walk is defined by the following rules.
# Pick a cell uniformly at random from cells. Start the random walk from there.
# Successor of current cell is chosen uniformly at random from the hook .
# Continue until you reach a corner cell .
Proposition: For a given corner cell of , we have
:
where .
Given this, summing over all corner cells gives as claimed.
The Surprising Mathematics of Longest Increasing Subsequences
by Dan Romik. Contains discussions of the hook length formula and several of its variants, with applications to the mathematics of longest increasing subsequences. Combinatorics
standard Young tableaux In mathematics, a Young tableau (; plural: tableaux) is a combinatorial object useful in representation theory and Schubert calculus. It provides a convenient way to describe the group representations of the symmetric and general linear groups ...
whose shape is a given Young diagram In mathematics, a Young tableau (; plural: tableaux) is a combinatorial object useful in representation theory and Schubert calculus. It provides a convenient way to describe the group representations of the symmetric and general linear groups ...
.
It has applications in diverse areas such as representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by ''representing'' their elements as linear transformations of vector spaces, and studies modules over these abstract algebraic structures. In essen ...
, probability
Probability is the branch of mathematics concerning numerical descriptions of how likely an Event (probability theory), event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and ...
, and algorithm analysis; for example, the problem of longest increasing subsequences. A related formula gives the number of semi-standard Young tableaux, which is a specialization of a Schur polynomial.
Definitions and statement
Let be a partition of . It is customary to interpret graphically as aYoung diagram In mathematics, a Young tableau (; plural: tableaux) is a combinatorial object useful in representation theory and Schubert calculus. It provides a convenient way to describe the group representations of the symmetric and general linear groups ...
, namely a left-justified array of square cells with rows of lengths .
A (standard) Young tableau of shape is a filling of the cells of the Young diagram with all the integers , with no repetition, such that each row and each column form increasing sequences.
For the cell in position , in the th row and th column, the hook is the set of cells such that and or and .
The hook length is the number of cells in .
The hook length formula expresses the number of standard Young tableaux of shape , denoted by or , as
:
where the product is over all cells of the Young diagram.
Examples
 The figure on the right shows hook lengths for the cells in the
The figure on the right shows hook lengths for the cells in the Young diagram In mathematics, a Young tableau (; plural: tableaux) is a combinatorial object useful in representation theory and Schubert calculus. It provides a convenient way to describe the group representations of the symmetric and general linear groups ...
, corresponding to the partition 9 = 4 + 3 + 1 + 1. The hook length formula gives the number of standard Young tableaux as:
:
A Catalan number
In combinatorial mathematics, the Catalan numbers are a sequence of natural numbers that occur in various counting problems, often involving recursively defined objects. They are named after the French-Belgian mathematician Eugène Charles C ...
counts Dyck paths with steps going up (U) interspersed with steps going down (D), such that at each step there are never more preceding D's than U's. These are in bijection with the Young tableaux of shape : a Dyck path corresponds to the tableau whose first row lists the positions of the U-steps, while the second row lists the positions of the D-steps. For example, UUDDUD correspond to the tableaux with rows 125 and 346.
This shows that , so the hook formula specializes to the well-known product formula
:
History
There are other formulas for , but the hook length formula is particularly simple and elegant. A less convenient formula expressing in terms of adeterminant
In mathematics, the determinant is a scalar value that is a function of the entries of a square matrix. It characterizes some properties of the matrix and the linear map represented by the matrix. In particular, the determinant is nonzero if ...
was deduced independently by Frobenius and Young in 1900 and 1902 respectively using algebraic methods.
MacMahon found an alternate proof for the Young–Frobenius formula in 1916 using difference methods.
The hook length formula itself was discovered in 1953 by Frame, Robinson, and Thrall as an improvement to the Young–Frobenius formula. Sagan describes the discovery as follows.
Despite the simplicity of the hook length formula, the Frame–Robinson–Thrall proof is not very insightful and does not provide any intuition for the role of the hooks. The search for a short, intuitive explanation befitting such a simple result gave rise to many alternate proofs.
Hillman and Grassl gave the first proof that illuminates the role of hooks in 1976 by proving a special case of the Stanley hook-content formula, which is known to imply the hook length formula.
Greene, Nijenhuis, and Wilf Wilf is a masculine given name, most commonly a diminutive form of Wilfred or Wilfrid. It is also a nickname and a surname.
People
Given name
* Wilfred Arthur (1919–2000), Australian World War II fighter ace
* Wilf Barber (1901–1968), Engl ...
found a probabilistic proof using the hook walk in which the hook lengths appear naturally in 1979.Greene, C., Nijenhuis, A. and Wilf, H. S. (1979). A probabilistic proof of a formula for the number of Young tableaux of a given shape. Advances in Mathematics
''Advances in Mathematics'' is a peer-reviewed scientific journal covering research on pure mathematics. It was established in 1961 by Gian-Carlo Rota. The journal publishes 18 issues each year, in three volumes.
At the origin, the journal aimed ...
31, 104–109.
Remmel adapted the original Frame–Robinson–Thrall proof into the first bijective proof for the hook length formula in 1982.
A direct bijective proof was first discovered by Franzblau and Zeilberger in 1982.
Zeilberger also converted the Greene–Nijenhuis–Wilf hook walk proof into a bijective proof in 1984. A simpler direct bijection was announced by Pak
Pak or PAK may refer to:
Places
* Pakistan (country code PAK)
* Pak, Afghanistan
* Pak Island, in the Admiralty Islands group of Papua New Guinea
* Pak Tea House, a café in Lahore, Punjab, Pakistan
Arts and entertainment
* PAK (band), an Amer ...
and Stoyanovskii in 1992, and its complete proof was presented by the pair and Novelli in 1997.
Meanwhile, the hook length formula has been generalized in several ways.
R. M. Thrall found the analogue to the hook length formula for shifted Young Tableaux in 1952. Sagan gave a shifted hook walk proof for the hook length formula for shifted Young tableaux in 1980.
Sagan and Yeh proved the hook length formula for binary trees using the hook walk in 1989. Proctor gave a poset generalization (see below).
Probabilistic proof
Knuth's heuristic argument
The hook length formula can be understood intuitively using the following heuristic, but incorrect, argument suggested by D. E. Knuth. Given that each element of a tableau is the smallest in its hook and filling the tableau shape at random, the probability that cell will contain the minimum element of the corresponding hook is the reciprocal of the hook length. Multiplying these probabilities over all and gives the formula. This argument is fallacious since the events are not independent. Knuth's argument is however correct for the enumeration of labellings on trees satisfying monotonicity properties analogous to those of a Young tableau. In this case, the 'hook' events in question are in fact independent events.Probabilistic proof using the hook walk
This is a probabilistic proof found by C. Greene, A. Nijenhuis, and H. S. Wilf in 1979. Define : We wish to show that . First, : where the sum runs over all Young diagrams obtained from by deleting one corner cell. (The maximal entry of the Young tableau of shape occurs at one of its corner cells, so deleting it gives a Young tableaux of shape .)
We define and , so it is enough to show the same recurrence
:
which would imply by induction. The above sum can be viewed as a sum of probabilities by writing it as
:
We therefore need to show that the numbers define a probability measure on the set of Young diagrams with . This is done in a constructive way by defining a random walk, called the hook walk, on the cells of the Young diagram , which eventually selects one of the corner cells of (which are in bijection with diagrams for which ). The hook walk is defined by the following rules.
# Pick a cell uniformly at random from cells. Start the random walk from there.
# Successor of current cell is chosen uniformly at random from the hook .
# Continue until you reach a corner cell .
Proposition: For a given corner cell of , we have
:
where .
Given this, summing over all corner cells gives as claimed.
where the sum runs over all Young diagrams obtained from by deleting one corner cell. (The maximal entry of the Young tableau of shape occurs at one of its corner cells, so deleting it gives a Young tableaux of shape .)
We define and , so it is enough to show the same recurrence
:
which would imply by induction. The above sum can be viewed as a sum of probabilities by writing it as
:
We therefore need to show that the numbers define a probability measure on the set of Young diagrams with . This is done in a constructive way by defining a random walk, called the hook walk, on the cells of the Young diagram , which eventually selects one of the corner cells of (which are in bijection with diagrams for which ). The hook walk is defined by the following rules.
# Pick a cell uniformly at random from cells. Start the random walk from there.
# Successor of current cell is chosen uniformly at random from the hook .
# Continue until you reach a corner cell .
Proposition: For a given corner cell of , we have
:
where .
Given this, summing over all corner cells gives as claimed.
Connection to representations of the symmetric group
The hook length formula is of great importance in the representation theory of the symmetric group , where the number is known to be equal to the dimension of the complex irreducible representation associated to .Detailed discussion
The complex irreducible representations of the symmetric group are indexed by partitions of (see Specht module) . Their characters are related to the theory of symmetric functions via the Hall inner product: : where is the Schur function associated to and is the power-sum symmetric function of the partition associated to the cycle decomposition of . For example, if then . Since the identity permutation has the form in cycle notation, , the formula says : The expansion of Schur functions in terms of monomial symmetric functions uses the Kostka numbers: : Then the inner product with is , because . Note that is equal to , so that from considering theregular representation
In mathematics, and in particular the theory of group representations, the regular representation of a group ''G'' is the linear representation afforded by the group action of ''G'' on itself by translation.
One distinguishes the left regular r ...
of , or combinatorially from the Robinson–Schensted–Knuth correspondence.
The computation also shows that:
:
This is the expansion of in terms of Schur functions using the coefficients given by the inner product, since .
The above equality can be proven also checking the coefficients of each monomial at both sides and using the Robinson–Schensted–Knuth correspondence or, more conceptually, looking at the decomposition of by irreducible modules, and taking characters. See Schur–Weyl duality.
Proof of hook formula using Frobenius formula
By the above considerations : so that : where is the Vandermonde determinant. For the partition , define for . For the following we need at least as many variables as rows in the partition, so from now on we work with variables . Each term is equal to : (See Schur function.) Since the vector is different for each partition, this means that the coefficient of in , denoted , is equal to . This is known as theFrobenius Character Formula In mathematics, specifically in representation theory, the Frobenius formula, introduced by G. Frobenius, computes the characters of irreducible representations of the symmetric group ''S'n''. Among the other applications, the formula can be use ...
, which gives one of the earliest proofs.
It remains only to simplify this coefficient. Multiplying
:
and
:
we conclude that our coefficient as
:
which can be written as
:
The latter sum is equal to the following determinant
:
which column-reduces to a Vandermonde determinant, and we obtain the formula
:
Note that is the hook length of the first box in each row of the Young diagram, and this expression is easily transformed into the desired form : one shows , where the latter product runs over the th row of the Young diagram.
Connection to longest increasing subsequences
The hook length formula also has important applications to the analysis of longest increasing subsequences in random permutations. If denotes a uniformly random permutation of order , denotes the maximal length of an increasing subsequence of , and denotes the expected (average) value of , Anatoly Vershik andSergei Kerov
Sergius is a male given name of Ancient Roman origin after the name of the Latin ''gens'' Sergia or Sergii of regal and republican ages. It is a common Christian name, in honor of Saint Sergius, or in Russia, of Saint Sergius of Radonezh, an ...
and independently Benjamin F. Logan and Lawrence A. Shepp showed that when is large, is approximately equal to . This answers a question originally posed by Stanislaw Ulam
Stanisław Marcin Ulam (; 13 April 1909 – 13 May 1984) was a Polish-American scientist in the fields of mathematics and nuclear physics. He participated in the Manhattan Project, originated the Teller–Ulam design of thermonuclear weapo ...
. The proof is based on translating the question via the Robinson–Schensted correspondence to a problem about the limiting shape of a random Young tableau chosen according to Plancherel measure. Since the definition of Plancherel measure involves the quantity , the hook length formula can then be used to perform an asymptotic analysis of the limit shape and thereby also answer the original question.
The ideas of Vershik–Kerov and Logan–Shepp were later refined by Jinho Baik, Percy Deift and Kurt Johansson, who were able to achieve a much more precise analysis of the limiting behavior of the maximal increasing subsequence length, proving an important result now known as the Baik–Deift–Johansson theorem. Their analysis again makes crucial use of the fact that has a number of good formulas, although instead of the hook length formula it made use of one of the determinantal expressions.
Related formulas
The formula for the number of Young tableaux of shape was originally derived from the Frobenius determinant formula in connection to representation theory: : Hook lengths can also be used to give a product representation to the generating function for the number of reverse plane partitions of a given shape. If is a partition of some integer , a reverse plane partition of with shape is obtained by filling in the boxes in the Young diagram with non-negative integers such that the entries add to and are non-decreasing along each row and down each column. The hook lengths can be defined as with Young tableaux. If denotes the number of reverse plane partitions of with shape , then the generating function can be written as : Stanley discovered another formula for the same generating function. In general, if is any poset with elements, the generating function for reverse -partitions is : where is a polynomial such that is the number oflinear extension
In order theory, a branch of mathematics, a linear extension of a partial order is a total order (or linear order) that is compatible with the partial order. As a classic example, the lexicographic order of totally ordered sets is a linear ext ...
s of .
In the case of a partition , we are considering the poset in its cells given by the relation
:.
So a linear extension is simply a standard Young tableau, i.e.
Proof of hook formula using Stanley's formula
Combining the two formulas for the generating functions we have : Both sides converge inside the disk of radius one and the following expression makes sense for : It would be violent to plug in 1, but the right hand side is a continuous function inside the unit disk and a polynomial is continuous everywhere so at least we can say : ApplyingL'Hôpital's rule
In calculus, l'Hôpital's rule or l'Hospital's rule (, , ), also known as Bernoulli's rule, is a theorem which provides a technique to evaluate limits of indeterminate forms. Application (or repeated application) of the rule often converts an ...
times yields the hook length formula
:
Semi-standard tableaux hook length formula
The Schur polynomial is the generating function of semistandard Young tableaux with shape and entries in . Specializing this to gives the number of semi-standard tableaux, which can be written in terms of hook lengths:The Young diagram corresponds to an irreducible representation of thespecial linear group
In mathematics, the special linear group of degree ''n'' over a field ''F'' is the set of matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion. This is the normal subgroup of the gen ...
, and the Schur polynomial is also the character of the diagonal matrix acting on this representation. The above specialization is thus the dimension of the irreducible representation, and the formula is an alternative to the more general Weyl dimension formula
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by . There is a closely related formula for the ch ...
.
We may refine this by taking the principal specialization of the Schur function in the variables :
:
where for the conjugate partition .
Skew shape formula
There is a generalization of this formula for skew shapes, : where the sum is taken over ''excited diagrams'' of shape and boxes distributed according to .Generalization to ''d''-complete posets
Young diagrams can be considered as finite order ideals in the poset , and standard Young tableaux are theirlinear extension
In order theory, a branch of mathematics, a linear extension of a partial order is a total order (or linear order) that is compatible with the partial order. As a classic example, the lexicographic order of totally ordered sets is a linear ext ...
s. Robert Proctor has given a generalization of the hook length formula to count linear extensions of a larger class of posets generalizing both trees and skew diagrams.
References
{{reflistExternal links
The Surprising Mathematics of Longest Increasing Subsequences
by Dan Romik. Contains discussions of the hook length formula and several of its variants, with applications to the mathematics of longest increasing subsequences. Combinatorics