History Of Lorentz Transformations

The history of Lorentz transformations comprises the development of linear transformations forming the Lorentz group or Poincaré group preserving the Lorentz interval $-x_^+\cdots+x_^$ and the Minkowski inner product $-x_y_+\cdots+x_y_$.

In mathematics, transformations equivalent to what was later known as Lorentz transformations in various dimensions were discussed in the 19th century in relation to the theory of quadratic forms, hyperbolic geometry, Möbius geometry, and sphere geometry, which is connected to the fact that the group of motions in hyperbolic space, the Möbius group or projective special linear group, and the Laguerre group are isomorphic to the Lorentz group.

In physics, Lorentz transformations became known at the beginning of the 20th century, when it was discovered that they exhibit the symmetry of Maxwell's equations. Subsequently, they became fundamental to all of physics, because they formed the basis of special relativity in which they exhibit the symmetry of Minkowski spacetime, making the speed of light invariant between different inertial frames. They relate the spacetime coordinates of two arbitrary inertial frames of reference with constant relative speed ''v''. In one frame, the position of an event is given by ''x,y,z'' and time ''t'', while in the other frame the same event has coordinates ''x′,y′,z′'' and ''t′''.

Mathematical prehistory

Using the coefficients of a symmetric matrix A, the associated bilinear form, and a linear transformations in terms of transformation matrix g, the Lorentz transformation is given if the following conditions are satisfied:

:$\begin\begin-x_^+\cdots+x_^ & =-x_^+\dots+x_^\\ -x_y_+\cdots+x_y_ & =-x_^y_^+\cdots+x_^y_^ \end \\ \hline \begin\mathbf'=\mathbf\cdot\mathbf\\ \mathbf=\mathbf^\cdot\mathbf' \end\\ \hline \begin\begin\mathbf\cdot\mathbf^\cdot\mathbf & =\mathbf^\\ \mathbf^\cdot\mathbf\cdot\mathbf & =\mathbf\\ \mathbf\cdot\mathbf\cdot\mathbf^ & =\mathbf \end \end\\ \hline \mathbf=(-1,1,\dots,1)\\ \det \mathbf=\pm1 \end$

It forms an indefinite orthogonal group called the Lorentz group O(1,n), while the case det g=+1 forms the restricted Lorentz group SO(1,n). The quadratic form becomes the Lorentz interval in terms of an indefinite quadratic form of Minkowski space (being a special case of pseudo-Euclidean space), and the associated bilinear form becomes the Minkowski inner product.Ratcliffe (1994), 3.1 and Theorem 3.1.4 and Exercise 3.1 Long before the advent of special relativity it was used in topics such as the Cayley–Klein metric, hyperboloid model and other models of hyperbolic geometry, computations of elliptic functions and integrals, transformation of indefinite quadratic forms, squeeze mappings of the hyperbola, group theory, Möbius transformations, spherical wave transformation, transformation of the Sine-Gordon equation, Biquaternion algebra, split-complex numbers, Clifford algebra, and others.

Electrodynamics and special relativity

Overview

In the special relativity, Lorentz transformations exhibit the symmetry of Minkowski spacetime by using a constant ''c'' as the speed of light, and a parameter ''v'' as the relative velocity between two inertial reference frames. Using the above conditions, the Lorentz transformation in 3+1 dimensions assume the form:

:$\begin-c^t^+x^+y^+z^=-c^t^+x^+y^+z^\\ \hline \left.\begint' & =\gamma\left(t-x\frac\right)\\ x' & =\gamma(x-vt)\\ y' & =y\\ z' & =z \end \\begint & =\gamma\left(t'+x\frac\right)\\ x & =\gamma(x'+vt')\\ y & =y'\\ z & =z' \end \end\Rightarrow\begin(ct'+x') & =(ct+x)\sqrt\\ (ct'-x') & =(ct-x)\sqrt \end$

In physics, analogous transformations have been introduced by Voigt (1887) related to an incompressible medium, and by Heaviside (1888), Thomson (1889), Searle (1896) and Lorentz (1892, 1895) who analyzed Maxwell's equations. They were completed by Larmor (1897, 1900) and Lorentz (1899, 1904), and brought into their modern form by Poincaré (1905) who gave the transformation the name of Lorentz. Eventually, Einstein (1905) showed in his development of special relativity that the transformations follow from the principle of relativity and constant light speed alone by modifying the traditional concepts of space and time, without requiring a mechanical aether in contradistinction to Lorentz and Poincaré. Minkowski (1907–1908) used them to argue that space and time are inseparably connected as spacetime.

Regarding special representations of the Lorentz transformations: Minkowski (1907–1908) and Sommerfeld (1909) used imaginary trigonometric functions, Frank (1909) and Varićak (1910) used hyperbolic functions, Bateman and Cunningham (1909–1910) used spherical wave transformations, Herglotz (1909–10) used Möbius transformations, Plummer (1910) and Gruner (1921) used trigonometric Lorentz boosts, Ignatowski (1910) derived the transformations without light speed postulate, Noether (1910) and Klein (1910) as well Conway (1911) and Silberstein (1911) used Biquaternions, Ignatowski (1910/11), Herglotz (1911), and others used vector transformations valid in arbitrary directions, Borel (1913–14) used Cayley–Hermite parameter,

Voigt (1887)

Woldemar Voigt (1887)Voigt (1887), p. 45 developed a transformation in connection with the Doppler effect and an incompressible medium, being in modern notation:Pais (1982), Kap. 6b

:$\begin\text & \text\\ \hline \left.\begin\xi_ & =x_-\varkappa t\\ \eta_ & =y_q\\ \zeta_ & =z_q\\ \tau & =t-\frac\\ q & =\sqrt \end \ & \beginx^ & =x-vt\\ y^ & =\frac\\ z^ & =\frac\\ t^ & =t-\frac\\ \frac & =\sqrt \end \end$

If the right-hand sides of his equations are multiplied by γ they are the modern Lorentz transformation. In Voigt's theory the speed of light is invariant, but his transformations mix up a relativistic boost together with a rescaling of space-time. Optical phenomena in free space are scale, conformal, and Lorentz invariant, so the combination is invariant too. For instance, Lorentz transformations can be extended by using factor $l$:Lorentz (1915/16), p. 197

:$x^=\gamma l\left(x-vt\right),\quad y^=ly,\quad z^=lz,\quad t^=\gamma l\left(t-x\frac\right)$.

''l''=1/γ gives the Voigt transformation, ''l''=1 the Lorentz transformation. But scale transformations are not a symmetry of all the laws of nature, only of electromagnetism, so these transformations cannot be used to formulate a principle of relativity in general. It was demonstrated by Poincaré and Einstein that one has to set ''l''=1 in order to make the above transformation symmetric and to form a group as required by the relativity principle, therefore the Lorentz transformation is the only viable choice.

Voigt sent his 1887 paper to Lorentz in 1908, and that was acknowledged in 1909:

Also Hermann Minkowski said in 1908 that the transformations which play the main role in the principle of relativity were first examined by Voigt in 1887. Voigt responded in the same paper by saying that his theory was based on an elastic theory of light, not an electromagnetic one. However, he concluded that some results were actually the same.Bucherer (1908), p. 762

Heaviside (1888), Thomson (1889), Searle (1896)

In 1888, Oliver HeavisideHeaviside (1888), p. 324 investigated the properties of charges in motion according to Maxwell's electrodynamics. He calculated, among other things, anisotropies in the electric field of moving bodies represented by this formula:

:$\mathrm=\left(\frac\right)\left(1-\frac\right)^$.

Consequently, Joseph John Thomson (1889)Thomson (1889), p. 12 found a way to substantially simplify calculations concerning moving charges by using the following mathematical transformation (like other authors such as Lorentz or Larmor, also Thomson implicitly used the Galilean transformation ''z-vt'' in his equation):

:$\begin\text & \text\\ \hline \left.\beginz & =\left\ ^z'\end \ & \beginz^=z-vt & =\frac\end \end$

Thereby, inhomogeneous electromagnetic wave equations are transformed into a Poisson equation.Miller (1981), 98–99 Eventually, George Frederick Charles SearleSearle (1886), p. 333 noted in (1896) that Heaviside's expression leads to a deformation of electric fields which he called "Heaviside-Ellipsoid" of axial ratio

:$\begin\text & \text\\ \hline \left.\begin & \sqrt:1:1\\ \alpha= & 1-\frac \end \ & \begin & \frac:1:1\\ \frac & =1-\frac \end \end$

Lorentz (1892, 1895)

In order to explain the aberration of light and the result of the Fizeau experiment in accordance with Maxwell's equations, Lorentz in 1892 developed a model ("Lorentz ether theory") in which the aether is completely motionless, and the speed of light in the aether is constant in all directions. In order to calculate the optics of moving bodies, Lorentz introduced the following quantities to transform from the aether system into a moving system (it's unknown whether he was influenced by Voigt, Heaviside, and Thomson)Lorentz (1892a), p. 141Miller (1982), 1.4 & 1.5

:$\begin\text & \text\\ \hline \left.\begin\mathfrak & =\fracx\\ t' & =t-\frac\mathfrak\\ \varepsilon & =\frac \end \ & \beginx^ & =\gamma x^=\gamma(x-vt)\\ t^ & =t-\frac=\gamma^\left(t-\frac\right)\\ \gamma\frac & =\frac \end \end$

where ''x^*'' is the Galilean transformation ''x-vt''. Except the additional γ in the time transformation, this is the complete Lorentz transformation. While ''t'' is the "true" time for observers resting in the aether, ''t′'' is an auxiliary variable only for calculating processes for moving systems. It is also important that Lorentz and later also Larmor formulated this transformation in two steps. At first an implicit Galilean transformation, and later the expansion into the "fictitious" electromagnetic system with the aid of the Lorentz transformation. In order to explain the negative result of the Michelson–Morley experiment, he (1892b)Lorentz (1892b), p. 141 introduced the additional hypothesis that also intermolecular forces are affected in a similar way and introduced length contraction in his theory (without proof as he admitted). The same hypothesis had been made previously by George FitzGerald in 1889 based on Heaviside's work. While length contraction was a real physical effect for Lorentz, he considered the time transformation only as a heuristic working hypothesis and a mathematical stipulation.

In 1895, Lorentz further elaborated on his theory and introduced the "theorem of corresponding states". This theorem states that a moving observer (relative to the ether) in his "fictitious" field makes the same observations as a resting observers in his "real" field for velocities to first order in ''v/c''. Lorentz showed that the dimensions of electrostatic systems in the ether and a moving frame are connected by this transformation:Lorentz (1895), p. 37

:$\begin\text & \text\\ \hline \left.\beginx & =x^\sqrt\\ y & =y^\\ z & =z^\\ t & =t^ \end \ & \beginx^=x-vt & =\frac\\ y & =y^\\ z & =z^\\ t & =t^ \end \end$

For solving optical problems Lorentz used the following transformation, in which the modified time variable was called "local time" () by him:Lorentz (1895), p. 49 for local time and p. 56 for spatial coordinates.

:$\begin\text & \text\\ \hline \left.\beginx & =\mathrm-\mathfrak_t\\ y & =\mathrm-\mathfrak_t\\ z & =\mathrm-\mathfrak_t\\ t^ & =t-\fracx-\fracy-\fracz \end \ & \beginx^ & =x-v_t\\ y^ & =y-v_t\\ z^ & =z-v_t\\ t^ & =t-\fracx'-\fracy'-\fracz' \end \end$

With this concept Lorentz could explain the Doppler effect, the aberration of light, and the Fizeau experiment.

Larmor (1897, 1900)

In 1897, Larmor extended the work of Lorentz and derived the following transformationLarmor (1897), p. 229

:$\begin\text & \text\\ \hline \left.\beginx_ & =x\varepsilon^\\ y_ & =y\\ z_ & =z\\ t^ & =t-vx/c^\\ dt_ & =dt^\varepsilon^\\ \varepsilon & =\left(1-v^/c^\right)^ \end \ & \beginx_ & =\gamma x^=\gamma(x-vt)\\ y_ & =y\\ z_ & =z\\ t^ & =t-\frac=t-\frac\\ dt_ & =\frac\\ \gamma^ & =\frac \end \end$

Larmor noted that if it is assumed that the constitution of molecules is electrical then the FitzGerald–Lorentz contraction is a consequence of this transformation, explaining the Michelson–Morley experiment. It's notable that Larmor was the first who recognized that some sort of time dilation is a consequence of this transformation as well, because "individual electrons describe corresponding parts of their orbits in times shorter for the estsystem in the ratio 1/γ". Larmor wrote his electrodynamical equations and transformations neglecting terms of higher order than ''(v/c)''² – when his 1897 paper was reprinted in 1929, Larmor added the following comment in which he described how they can be made valid to all orders of ''v/c'':Larmor (1897/1929), p. 39

In line with that comment, in his book Aether and Matter published in 1900, Larmor used a modified local time ''t″=t′-εvx′/c²'' instead of the 1897 expression ''t′=t-vx/c²'' by replacing ''v/c''² with ''εv/c''², so that ''t″'' is now identical to the one given by Lorentz in 1892, which he combined with a Galilean transformation for the ''x′, y′, z′, t′'' coordinates:Larmor (1900), p. 168

:$\begin\text & \text\\ \hline \left.\beginx^ & =x-vt\\ y^ & =y\\ z^ & =z\\ t^ & =t\\ t^ & =t^-\varepsilon vx^/c^ \end \ & \beginx^ & =x-vt\\ y^ & =y\\ z^ & =z\\ t^ & =t\\ t^=t^-\frac & =\gamma^\left(t-\frac\right) \end \end$

Larmor knew that the Michelson–Morley experiment was accurate enough to detect an effect of motion depending on the factor ''(v/c)''², and so he sought the transformations which were "accurate to second order" (as he put it). Thus he wrote the final transformations (where ''x′=x-vt'' and ''t″'' as given above) as:Larmor (1900), p. 174

:$\begin\text & \text\\ \hline \left.\beginx_ & =\varepsilon^x^\\ y_ & =y^\\ z_ & =z^\\ dt_ & =\varepsilon^dt^=\varepsilon^\left(dt^-\frac\varepsilon dx^\right)\\ t_ & =\varepsilon^t^-\frac\varepsilon^x^ \end \ & \beginx_ & =\gamma x^=\gamma(x-vt)\\ y_ & =y'=y\\ z_ & =z'=z\\ dt_ & =\frac=\frac\left(dt^-\frac\right)=\gamma\left(dt-\frac\right)\\ t_ & =\frac-\frac=\gamma\left(t-\frac\right) \end \end$

by which he arrived at the complete Lorentz transformation. Larmor showed that Maxwell's equations were invariant under this two-step transformation, "to second order in ''v/c''" – it was later shown by Lorentz (1904) and Poincaré (1905) that they are indeed invariant under this transformation to all orders in ''v/c''.

Larmor gave credit to Lorentz in two papers published in 1904, in which he used the term "Lorentz transformation" for Lorentz's first order transformations of coordinates and field configurations:

Lorentz (1899, 1904)

Also Lorentz extended his theorem of corresponding states in 1899. First he wrote a transformation equivalent to the one from 1892 (again, ''x''* must be replaced by ''x-vt''):Lorentz (1899), p. 429

:$\begin\text & \text\\ \hline \left.\beginx^ & =\fracx\\ y^ & =y\\ z^ & =z\\ t^ & =t-\fracx \end \ & \beginx^ & =\gamma x^=\gamma(x-vt)\\ y^ & =y\\ z^ & =z\\ t^ & =t-\frac=\gamma^\left(t-\frac\right) \end \end$

Then he introduced a factor ε of which he said he has no means of determining it, and modified his transformation as follows (where the above value of ''t′'' has to be inserted):Lorentz (1899), p. 439

:$\begin\text & \text\\ \hline \left.\beginx & =\fracx^\\ y & =\varepsilon y^\\ z & =\varepsilon x^\\ t^ & =k\varepsilon t^\\ k & =\frac \end \ & \beginx^=x-vt & =\fracx^\\ y & =\varepsilon y^\\ z & =\varepsilon z^\\ t^=\gamma^\left(t-\frac\right) & =\gamma\varepsilon t^\\ \gamma & =\frac \end \end$

This is equivalent to the complete Lorentz transformation when solved for ''x″'' and ''t″'' and with ε=1. Like Larmor, Lorentz noticed in 1899Lorentz (1899), p. 442 also some sort of time dilation effect in relation to the frequency of oscillating electrons ''"that in ''S'' the time of vibrations be ''kε'' times as great as in ''S₀''"'', where ''S₀'' is the aether frame.

In 1904 he rewrote the equations in the following form by setting ''l''=1/ε (again, ''x''* must be replaced by ''x-vt''):Lorentz (1904), p. 812

:$\begin\text & \text\\ \hline \left.\beginx^ & =klx\\ y^ & =ly\\ z^ & =lz\\ t' & =\fract-kl\fracx \end \ & \beginx^ & =\gamma lx^=\gamma l(x-vt)\\ y^ & =ly\\ z^ & =lz\\ t^ & =\frac-\frac=\gamma l\left(t-\frac\right) \end \end$

Under the assumption that ''l=1'' when ''v''=0, he demonstrated that ''l=1'' must be the case at all velocities, therefore length contraction can only arise in the line of motion. So by setting the factor ''l'' to unity, Lorentz's transformations now assumed the same form as Larmor's and are now completed. Unlike Larmor, who restricted himself to show the covariance of Maxwell's equations to second order, Lorentz tried to widen its covariance to all orders in ''v/c''. He also derived the correct formulas for the velocity dependence of electromagnetic mass, and concluded that the transformation formulas must apply to all forces of nature, not only electrical ones.Lorentz (1904), p. 826 However, he didn't achieve full covariance of the transformation equations for charge density and velocity. When the 1904 paper was reprinted in 1913, Lorentz therefore added the following remark:

Lorentz's 1904 transformation was cited and used by Alfred Bucherer in July 1904:Bucherer, p. 129; Definition of s on p. 32

:$x^=\sqrtx,\quad y^=y,\quad z^=z,\quad t'=\frac-\sqrt\fracx,\quad s=1-\frac$

or by Wilhelm Wien in July 1904:Wien (1904), p. 394

:$x=kx',\quad y=y',\quad z=z',\quad t'=kt-\fracx$

or by Emil Cohn in November 1904 (setting the speed of light to unity):Cohn (1904a), pp. 1296-1297

:$x=\frac,\quad y=y_,\quad z=z_,\quad t=kt_,\quad t_=t_-w\cdot r_,\quad k^=\frac$

or by Richard Gans in February 1905:Gans (1905), p. 169

:$x^=kx,\quad y^=y,\quad z^=z,\quad t'=\frac-\frac,\quad k^=\frac$

Poincaré (1900, 1905)

Local time

Neither Lorentz or Larmor gave a clear physical interpretation of the origin of local time. However, Henri Poincaré in 1900 commented on the origin of Lorentz's "wonderful invention" of local time. He remarked that it arose when clocks in a moving reference frame are synchronised by exchanging signals which are assumed to travel with the same speed $c$ in both directions, which lead to what is nowadays called relativity of simultaneity, although Poincaré's calculation does not involve length contraction or time dilation.Poincaré (1900), pp. 272–273 In order to synchronise the clocks here on Earth (the ''x*, t''* frame) a light signal from one clock (at the origin) is sent to another (at ''x''*), and is sent back. It's supposed that the Earth is moving with speed ''v'' in the ''x''-direction (= ''x''*-direction) in some rest system (''x, t'') (''i.e.'' the luminiferous aether system for Lorentz and Larmor). The time of flight outwards is

:$\delta t_=\frac$

and the time of flight back is

:$\delta t_=\frac$.

The elapsed time on the clock when the signal is returned is ''δt_a+δt_b'' and the time ''t*=(δt_a+δt_b)/2'' is ascribed to the moment when the light signal reached the distant clock. In the rest frame the time ''t=δt_a'' is ascribed to that same instant. Some algebra gives the relation between the different time coordinates ascribed to the moment of reflection. Thus

:$t^=t-\frac$

identical to Lorentz (1892). By dropping the factor γ² under the assumption that $\tfrac\ll1$, Poincaré gave the result ''t*=t-vx*/c²'', which is the form used by Lorentz in 1895.

Similar physical interpretations of local time were later given by Emil Cohn (1904)Cohn (1904b), p. 1408 and Max Abraham (1905).Abraham (1905), § 42

Lorentz transformation

On June 5, 1905 (published June 9) Poincaré formulated transformation equations which are algebraically equivalent to those of Larmor and Lorentz and gave them the modern form:Poincaré (1905), p. 1505

:$\beginx^ & =kl(x+\varepsilon t)\\ y^ & =ly\\ z^ & =lz\\ t' & =kl(t+\varepsilon x)\\ k & =\frac \end$.

Apparently Poincaré was unaware of Larmor's contributions, because he only mentioned Lorentz and therefore used for the first time the name "Lorentz transformation". Poincaré set the speed of light to unity, pointed out the group characteristics of the transformation by setting ''l''=1, and modified/corrected Lorentz's derivation of the equations of electrodynamics in some details in order to fully satisfy the principle of relativity, ''i.e.'' making them fully Lorentz covariant.

In July 1905 (published in January 1906)Poincaré (1905/06), pp. 129ff Poincaré showed in detail how the transformations and electrodynamic equations are a consequence of the principle of least action; he demonstrated in more detail the group characteristics of the transformation, which he called Lorentz group, and he showed that the combination ''x²+y²+z²-t²'' is invariant. He noticed that the Lorentz transformation is merely a rotation in four-dimensional space about the origin by introducing $ct\sqrt$ as a fourth imaginary coordinate, and he used an early form of four-vectors. He also formulated the velocity addition formula, which he had already derived in unpublished letters to Lorentz from May 1905:Poincaré (1905/06), p. 144

:$\xi'=\frac,\ \eta'=\frac$.

Einstein (1905) – Special relativity

On June 30, 1905 (published September 1905) Einstein published what is now called special relativity and gave a new derivation of the transformation, which was based only on the principle of relativity and the principle of the constancy of the speed of light. While Lorentz considered "local time" to be a mathematical stipulation device for explaining the Michelson-Morley experiment, Einstein showed that the coordinates given by the Lorentz transformation were in fact the inertial coordinates of relatively moving frames of reference. For quantities of first order in ''v/c'' this was also done by Poincaré in 1900, while Einstein derived the complete transformation by this method. Unlike Lorentz and Poincaré who still distinguished between real time in the aether and apparent time for moving observers, Einstein showed that the transformations applied to the kinematics of moving frames.

The notation for this transformation is equivalent to Poincaré's of 1905, except that Einstein didn't set the speed of light to unity:Einstein (1905), p. 902

:$\begin\tau & =\beta\left(t-\fracx\right)\\ \xi & =\beta(x-vt)\\ \eta & =y\\ \zeta & =z\\ \beta & =\frac \end$

Einstein also defined the velocity addition formula:Einstein (1905), § 5 and § 9

:$\beginx=\fract,\ y=\fracw_t\\ U^=\left(\frac\right)^+\left(\frac\right)^,\ w^=w_^+w_^,\ \alpha=\operatorname\frac\\ U=\frac \end\left, \begin\frac=u_\\ \frac=u_\\ \frac=u_ \end\right.$

and the light aberration formula:Einstein (1905), § 7

:$\cos\varphi'=\frac$

Minkowski (1907–1908) – Spacetime

The work on the principle of relativity by Lorentz, Einstein, Planck, together with Poincaré's four-dimensional approach, were further elaborated and combined with the hyperboloid model by Hermann Minkowski in 1907 and 1908.Minkowski (1907/15), pp. 927ffMinkowski (1907/08), pp. 53ff Minkowski particularly reformulated electrodynamics in a four-dimensional way (Minkowski spacetime). For instance, he wrote ''x, y, z, it'' in the form ''x₁, x₂, x₃, x₄''. By defining ψ as the angle of rotation around the ''z''-axis, the Lorentz transformation assumes the form (with ''c''=1):Minkowski (1907/08), p. 59

:$\beginx'_ & =x_\\ x'_ & =x_\\ x'_ & =x_\cos i\psi+x_\sin i\psi\\ x'_ & =-x_\sin i\psi+x_\cos i\psi\\ \cos i\psi & =\frac \end$

Even though Minkowski used the imaginary number iψ, he for once directly used the tangens hyperbolicus in the equation for velocity

:$-i\tan i\psi=\frac=q$ with $\psi=\frac\ln\frac$.

Minkowski's expression can also by written as ψ=atanh(q) and was later called rapidity. He also wrote the Lorentz transformation in matrix form:Minkowski (1907/08), pp. 65–66, 81–82

:$\beginx_^+x_^+x_^+x_^=x_^+x_^+x_^+x_^\\ \left(x_^=x',\ x_^=y',\ x_^=z',\ x_^=it'\right)\\ -x^-y^-z^+t^=-x^-y^-z^+t^\\ \hline x_=\alpha_x_^+\alpha_x_^+\alpha_x_^+\alpha_x_^\\ \mathrm=\mathrm \end$

As a graphical representation of the Lorentz transformation he introduced the Minkowski diagram, which became a standard tool in textbooks and research articles on relativity:Minkowski (1908/09), p. 77

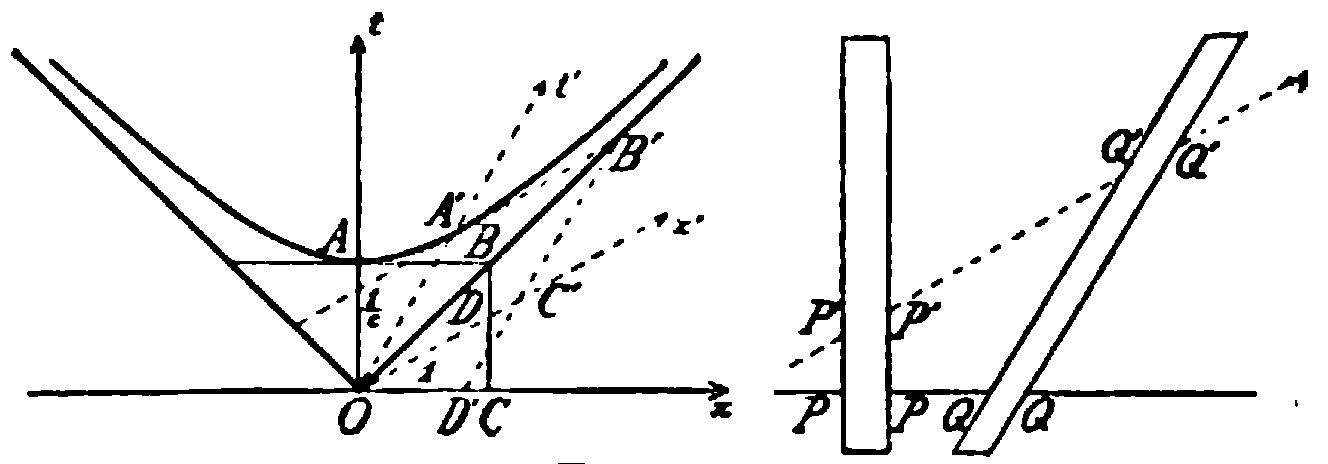
Sommerfeld (1909) – Spherical trigonometry

Using an imaginary rapidity such as Minkowski, Arnold Sommerfeld (1909) formulated the Lorentz boost and the relativistic velocity addition in terms of trigonometric functions and the spherical law of cosines:Sommerfeld (1909), p. 826ff.

:$\begin\left.\begin x'= & x\ \cos\varphi+l\ \sin\varphi, & y'=y\\ l'= & -x\ \sin\varphi+l\ \cos\varphi, & z'=z \end\right\} \\ \left(\operatorname\varphi=i\beta,\ \cos\varphi=\frac,\ \sin\varphi=\frac\right)\\ \hline \beta=\frac\operatorname\left(\varphi_+\varphi_\right)=\frac\frac=\frac\\ \cos\varphi=\cos\varphi_\cos\varphi_-\sin\varphi_\sin\varphi_\cos\alpha\\ v^=\frac \end$

Frank (1909) – Hyperbolic functions

Hyperbolic functions were used by Philipp Frank (1909), who derived the Lorentz transformation using ''ψ'' as rapidity:Frank (1909), pp. 423-425

:$\beginx'=x\varphi(a)\,\,\psi+t\varphi(a)\,\,\psi\\ t'=-x\varphi(a)\,\,\psi+t\varphi(a)\,\,\psi\\ \hline \,\psi=-a,\ \,\psi=\frac,\ \,\psi=\frac,\ \varphi(a)=1\\ \hline x'=\frac,\ y'=y,\ z'=z,\ t'=\frac \end$

Bateman and Cunningham (1909–1910) – Spherical wave transformation

In line with Sophus Lie's (1871) research on the relation between sphere transformations with an imaginary radius coordinate and 4D conformal transformations, it was pointed out by Bateman and Cunningham (1909–1910), that by setting ''u=ict'' as the imaginary fourth coordinates one can produce spacetime conformal transformations. Not only the quadratic form $\lambda\left(dx^+dy^+dz^+du^\right)$, but also Maxwells equations are covariant with respect to these transformations, irrespective of the choice of λ. These variants of conformal or Lie sphere transformations were called spherical wave transformations by Bateman.Bateman (1909/10), pp. 223ffCunningham (1909/10), pp. 77ff However, this covariance is restricted to certain areas such as electrodynamics, whereas the totality of natural laws in inertial frames is covariant under the Lorentz group.Klein (1910) In particular, by setting λ=1 the Lorentz group can be seen as a 10-parameter subgroup of the 15-parameter spacetime conformal group .

Bateman (1910–12) also alluded to the identity between the Laguerre inversion and the Lorentz transformations. In general, the isomorphism between the Laguerre group and the Lorentz group was pointed out by Élie Cartan (1912, 1915–55),Cartan (1912), p. 23 Henri Poincaré (1912–21)Poincaré (1912/21), p. 145 and others.

Herglotz (1909/10) – Möbius transformation

Following Felix Klein (1889–1897) and Fricke & Klein (1897) concerning the Cayley absolute, hyperbolic motion and its transformation, Gustav Herglotz (1909–10) classified the one-parameter Lorentz transformations as loxodromic, hyperbolic, parabolic and elliptic. The general case (on the left) and the hyperbolic case equivalent to Lorentz transformations or squeeze mappings are as follows:Herglotz (1909/10), pp. 404-408

:$\left.\beginz_^+z_^+z_^-z_^=0\\ z_=x,\ z_=y,\ z_=z,\ z_=t\\ Z=\frac=\frac,\ Z'=\frac\\ Z=\frac \end\\beginZ=Z'e^\\ \beginx & =x', & t-z & =(t'-z')e^\\ y & =y', & t+z & =(t'+z')e^ \end \end$

Varićak (1910) – Hyperbolic functions

Following Sommerfeld (1909), hyperbolic functions were used by Vladimir Varićak in several papers starting from 1910, who represented the equations of special relativity on the basis of hyperbolic geometry in terms of Weierstrass coordinates. For instance, by setting ''l=ct'' and ''v/c=tanh(u)'' with ''u'' as rapidity he wrote the Lorentz transformation:Varićak (1910), p. 93

:$\beginl' & =-x\operatornameu+l\operatornameu,\\ x' & =x\operatornameu-l\operatornameu,\\ y' & =y,\quad z'=z,\\ \operatornameu & =\frac \end$

and showed the relation of rapidity to the Gudermannian function and the angle of parallelism:

:$\frac=\operatornameu=\operatorname\psi=\sin\operatorname(u)=\cos\Pi(u)$

He also related the velocity addition to the hyperbolic law of cosines:Varićak (1910), p. 94

:$\begin\operatorname=\operatorname\operatorname ch+\operatorname\operatorname\cos\alpha\\ \operatorname=\frac,\ \operatorname=\frac\\ v=\sqrt\ \left(a=\frac\right) \end$

Subsequently, other authors such as E. T. Whittaker (1910) or Alfred Robb (1911, who coined the name rapidity) used similar expressions, which are still used in modern textbooks.

Plummer (1910) – Trigonometric Lorentz boosts

w:Henry Crozier Keating Plummer (1910) defined the Lorentz boost in terms of trigonometric functionsPlummer (1910), p. 256

:$\begin\tau=t\sec\beta-x\tan\beta/U\\ \xi=x\sec\beta-Ut\tan\beta\\ \eta=y,\ \zeta=z,\\ \hline \sin\beta=v/U \end$

Ignatowski (1910)

While earlier derivations and formulations of the Lorentz transformation relied from the outset on optics, electrodynamics, or the invariance of the speed of light, Vladimir Ignatowski (1910) showed that it is possible to use the principle of relativity (and related group theoretical principles) alone, in order to derive the following transformation between two inertial frames:Ignatowski (1910), pp. 973–974Ignatowski (1910/11), p. 13

:$\begindx' & =p\ dx-pq\ dt\\ dt' & =-pqn\ dx+p\ dt\\ p & =\frac \end$

The variable ''n'' can be seen as a space-time constant whose value has to be determined by experiment or taken from a known physical law such as electrodynamics. For that purpose, Ignatowski used the above-mentioned Heaviside ellipsoid representing a contraction of electrostatic fields by ''x''/γ in the direction of motion. It can be seen that this is only consistent with Ignatowski's transformation when ''n=1/c''², resulting in ''p''=γ and the Lorentz transformation. With ''n''=0, no length changes arise and the Galilean transformation follows. Ignatowski's method was further developed and improved by Philipp Frank and Hermann Rothe (1911, 1912),Frank & Rothe (1911), pp. 825ff; (1912), p. 750ff. with various authors developing similar methods in subsequent years.Baccetti (2011), see references 1–25 therein.

Noether (1910), Klein (1910) – Quaternions

Felix Klein (1908) described Cayley's (1854) 4D quaternion multiplications as "Drehstreckungen" (orthogonal substitutions in terms of rotations leaving invariant a quadratic form up to a factor), and pointed out that the modern principle of relativity as provided by Minkowski is essentially only the consequent application of such Drehstreckungen, even though he didn't provide details.Klein (1908), p. 165

In an appendix to Klein's and Sommerfeld's "Theory of the top" (1910), Fritz Noether showed how to formulate hyperbolic rotations using biquaternions with $\omega=\sqrt$, which he also related to the speed of light by setting ω²=-''c''². He concluded that this is the principal ingredient for a rational representation of the group of Lorentz transformations:Noether (1910), pp. 939–943

:$\beginV=\frac\\ \hline X^+Y^+Z^+\omega^S^=x^+y^+z^+\omega^s^\\ \hline \beginV & =Xi+Yj+Zk+\omega S\\ v & =xi+yj+zk+\omega s\\ Q_ & =(+Ai+Bj+Ck+D)+\omega(A'i+B'j+C'k+D')\\ Q_ & =(-Ai-Bj-Ck+D)+\omega(A'i+B'j+C'k-D')\\ T_T_ & =T_^=T_^=A^+B^+C^+D^+\omega^\left(A^+B^+C^+D^\right) \end \end$

Besides citing quaternion related standard works by Arthur Cayley (1854), Noether referred to the entries in Klein's encyclopedia by Eduard Study (1899) and the French version by Élie Cartan (1908). Cartan's version contains a description of Study's dual numbers, Clifford's biquaternions (including the choice $\omega=\sqrt$ for hyperbolic geometry), and Clifford algebra, with references to Stephanos (1883), Buchheim (1884–85), Vahlen (1901–02) and others.

Citing Noether, Klein himself published in August 1910 the following quaternion substitutions forming the group of Lorentz transformations:Klein (1910), p. 300

:$\begin\begin & \left(i_x'+i_y'+i_z'+ict'\right)\\ & \quad-\left(i_x_+i_y_+i_z_+ict_\right) \end =\frac\\ \hline \text\\ AA'+BB'+CC'+DD'=0\\ A^+B^+C^+D^>A^+B^+C^+D^ \end$

or in March 1911Klein (1911), pp. 602ff.

:$\beging'=\frac\\ \hline \beging & =\sqrtct+ix+jy+kz\\ g' & =\sqrtct'+ix'+jy'+kz'\\ p & =(D+\sqrtD')+i(A+\sqrtA')+j(B+\sqrtB')+k(C+\sqrtC')\\ \pi & =(D-\sqrtD')-i(A-\sqrtA')-j(B-\sqrtB')-k(C-\sqrtC')\\ M & =\left(A^+B^+C^+D^\right)-\left(A^+B^+C^+D^\right)\\ & AA'+BB'+CC'+DD'=0\\ & A^+B^+C^+D^>A^+B^+C^+D^ \end \end$

Conway (1911), Silberstein (1911) – Quaternions

Arthur W. Conway in February 1911 explicitly formulated quaternionic Lorentz transformations of various electromagnetic quantities in terms of velocity λ:Conway (1911), p. 8

:$\begin\begin\mathtt & =\mathbf^\mathtt'\mathbf^\\ \mathtt & =\mathbf\mathtt'\mathbf^ \end \\ e=\mathbf^e'\mathbf^\\ \hline a=\left(1-hc^\lambda\right)^\left(1+c^\lambda^\right)^ \end$

Also Ludwik Silberstein in November 1911Silberstein (1911/12), p. 793 as well as in 1914, formulated the Lorentz transformation in terms of velocity ''v'':

:$\beginq'=QqQ\\ \hline \beginq & =\mathbf+l=xi+yj+zk+\iota ct\\ q & '=\mathbf'+l'=x'i+y'j+z'k+\iota ct'\\ Q & =\frac\left(\sqrt+\mathrm\sqrt\right)\\ & =\cos\alpha+\mathrm\sin\alpha=e^\\ & \left\ \end \end$

Silberstein cites Cayley (1854, 1855) and Study's encyclopedia entry (in the extended French version of Cartan in 1908), as well as the appendix of Klein's and Sommerfeld's book.

Ignatowski (1910/11), Herglotz (1911), and others – Vector transformation

Vladimir Ignatowski (1910, published 1911) showed how to reformulate the Lorentz transformation in order to allow for arbitrary velocities and coordinates:Ignatowski (1910/11a), p. 23; (1910/11b), p. 22

:\begin\begin\mathfrak =\frac & \left, \begin\mathfrak' & =\mathfrak+(p-1)\mathfrak_\cdot\mathfrak_\mathfrak-pqb\mathfrak_\\
b' & =pb-pqn\mathfrak\mathfrak_\\
\\
\mathfrak & =\mathfrak'+(p-1)\mathfrak_\cdot\mathfrak_\mathfrak'+pqb'\mathfrak_\\
b & =pb'+pqn\mathfrak'\mathfrak_
\end
\right.\end\\
\left mathfrak=\mathbf,\ \mathfrak=\mathbf,\ b=t,\ \mathfrak_=\frac,\ p=\gamma,\ n=\frac\right\end

Gustav Herglotz (1911)Herglotz (1911), p. 497 also showed how to formulate the transformation in order to allow for arbitrary velocities and coordinates v=''(v_x, v_y, v_z)'' and r=''(x, y, z)'':

:$\begin\text & \text\\ \hline \left.\beginx^ & =x+\alpha u(ux+vy+wz)-\beta ut\\ y^ & =y+\alpha v(ux+vy+wz)-\beta vt\\ z^ & =z+\alpha w(ux+vy+wz)-\beta wt\\ t^ & =-\beta(ux+vy+wz)+\beta t\\ & \alpha=\frac,\ \beta=\frac \end \ & \beginx' & =x+\alpha v_\left(v_x+v_y+v_z\right)-\gamma v_t\\ y' & =y+\alpha v_\left(v_x+v_y+v_z\right)-\gamma v_t\\ z' & =z+\alpha v_\left(v_x+v_y+v_z\right)-\gamma v_t\\ t' & =-\gamma\left(v_x+v_y+v_z\right)+\gamma t\\ & \alpha=\frac,\ \gamma=\frac \end \end$

This was simplified using vector notation by Ludwik Silberstein (1911 on the left, 1914 on the right):Silberstein (1911/12), p. 792; (1914), p. 123

:\begin
\begin\mathbf' & =\mathbf+(\gamma-1)(\mathbf)\mathbf+i\beta\gamma lu\\
l' & =\gamma\left -i\beta(\mathbf)\right\end
& \begin\mathbf' & =\mathbf+\left frac(\mathbf)-\gamma t\rightmathbf\\
t' & =\gamma\left -\frac(\mathbf)\right\end
\end

Equivalent formulas were also given by Wolfgang Pauli (1921), with Erwin Madelung (1922) providing the matrix form

:$\begin & x & y & z & t\\ \hline x' & 1-\frac\left(1-\frac\right) & -\frac\left(1-\frac\right) & -\frac\left(1-\frac\right) & \frac\\ y' & -\frac\left(1-\frac\right) & 1-\frac\left(1-\frac\right) & -\frac\left(1-\frac\right) & \frac\\ z' & -\frac\left(1-\frac\right) & -\frac\left(1-\frac\right) & 1-\frac\left(1-\frac\right) & \frac\\ t' & \frac & \frac & \frac & \frac \end$

These formulas were called "general Lorentz transformation without rotation" by Christian Møller (1952),Møller (1952/55), pp. 41–43 who in addition gave an even more general Lorentz transformation in which the Cartesian axes have different orientations, using a rotation operator $\mathfrak$. In this case, v′=''(v′_x, v′_y, v′_z)'' is not equal to -v=''(-v_x, -v_y, -v_z)'', but the relation $\mathbf'=-\mathfrak\mathbf$ holds instead, with the result

:$\begin \begin\mathbf' & =\mathfrak^\mathbf-\mathbf'\left\ \\ t' & =\gamma\left(t-(\mathbf\cdot\mathbf)/c^\right) \end \end$

Borel (1913–14) – Cayley–Hermite parameter

Émile Borel (1913) started by demonstrating Euclidean motions using Euler-Rodrigues parameter in three dimensions, and Cayley's (1846) parameter in four dimensions. Then he demonstrated the connection to indefinite quadratic forms expressing hyperbolic motions and Lorentz transformations. In three dimensions:Borel (1913/14), p. 39

:$\beginx^+y^-z^-1=0\\ \hline \\ \left(\delta=\lambda^+\mu^-\rho^-\nu^\right)\\ \lambda=\nu=0\rightarrow\text \end$

In four dimensions:Borel (1913/14), p. 41

:$\beginF=\left(x_-x_\right)^+\left(y_-y_\right)^+\left(z_-z_\right)^-\left(t_-t_\right)^\\ \hline \\ \left(\alpha^+\beta^+\gamma^-\lambda^-\mu^-\nu^=-1\right) \end$

Gruner (1921) – Trigonometric Lorentz boosts

In order to simplify the graphical representation of Minkowski space, Paul Gruner (1921) (with the aid of Josef Sauter) developed what is now called Loedel diagrams, using the following relations:Gruner (1921a),

:$\beginv=\alpha\cdot c;\quad\beta=\frac\\ \sin\varphi=\alpha;\quad\beta=\frac;\quad\alpha\beta=\tan\varphi\\ \hline x'=\frac-t\cdot\tan\varphi,\quad t'=\frac-x\cdot\tan\varphi \end$

In another paper Gruner used the alternative relations:Gruner (1921b)

:$\begin\alpha=\frac;\ \beta=\frac;\\ \cos\theta=\alpha=\frac;\ \sin\theta=\frac;\ \cot\theta=\alpha\cdot\beta\\ \hline x'=\frac-t\cdot\cot\theta,\quad t'=\frac-x\cdot\cot\theta \end$

See also

* Derivations of the Lorentz transformations
* History of special relativity

References

Historical mathematical sources

Historical relativity sources

*
*
*
*
*
*
*. For Minkowski's and Voigt's statements see p. 762.
*
*
*
*
*
*. See also
English translation

*
*
*
*
*
*
*
*
*; English translation by David Delphenich
On the mechanics of deformable bodies from the standpoint of relativity theory

*
*
*
*
*
*
*
*
* (Reprint of Larmor (1897) with new annotations by Larmor.)
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*. See also th
English translation

*
*
*
* Written by Poincaré in 1912, printed in Acta Mathematica in 1914 though belatedly published in 1921.
*
*
*
*
*
*
*
*

Secondary sources

*
*
*
*
*
*
*
* See also "Michelson, FitzGerald and Lorentz: the origins of relativity revisited"
Online

*
* (Only pages 1–21 were published in 1915, the entire article including pp. 39–43 concerning the groups of Laguerre and Lorentz was posthumously published in 1955 in Cartan's collected papers, and was reprinted in the Encyclopédie in 1991.)
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*; First edition 1911, second expanded edition 1913, third expanded edition 1919.
*
*
*
*
*
*
*
*
*
*
*
*
*
In English:
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*

External links

*Mathpages

{{DEFAULTSORT:Lorentz transformations
Equations
History of physics
Hendrik Lorentz
Historical treatment of quaternions