Gibbs Sampling on:
[Wikipedia]
[Google]
[Amazon]
In statistics, Gibbs sampling or a Gibbs sampler is a
 The following algorithm details a generic Gibbs sampler:
Note that Gibbs sampler is operated by the iterative Monte Carlo scheme within a cycle. The number of samples drawn by the above algorithm formulates Markov Chains with the invariant distribution to be the target density .
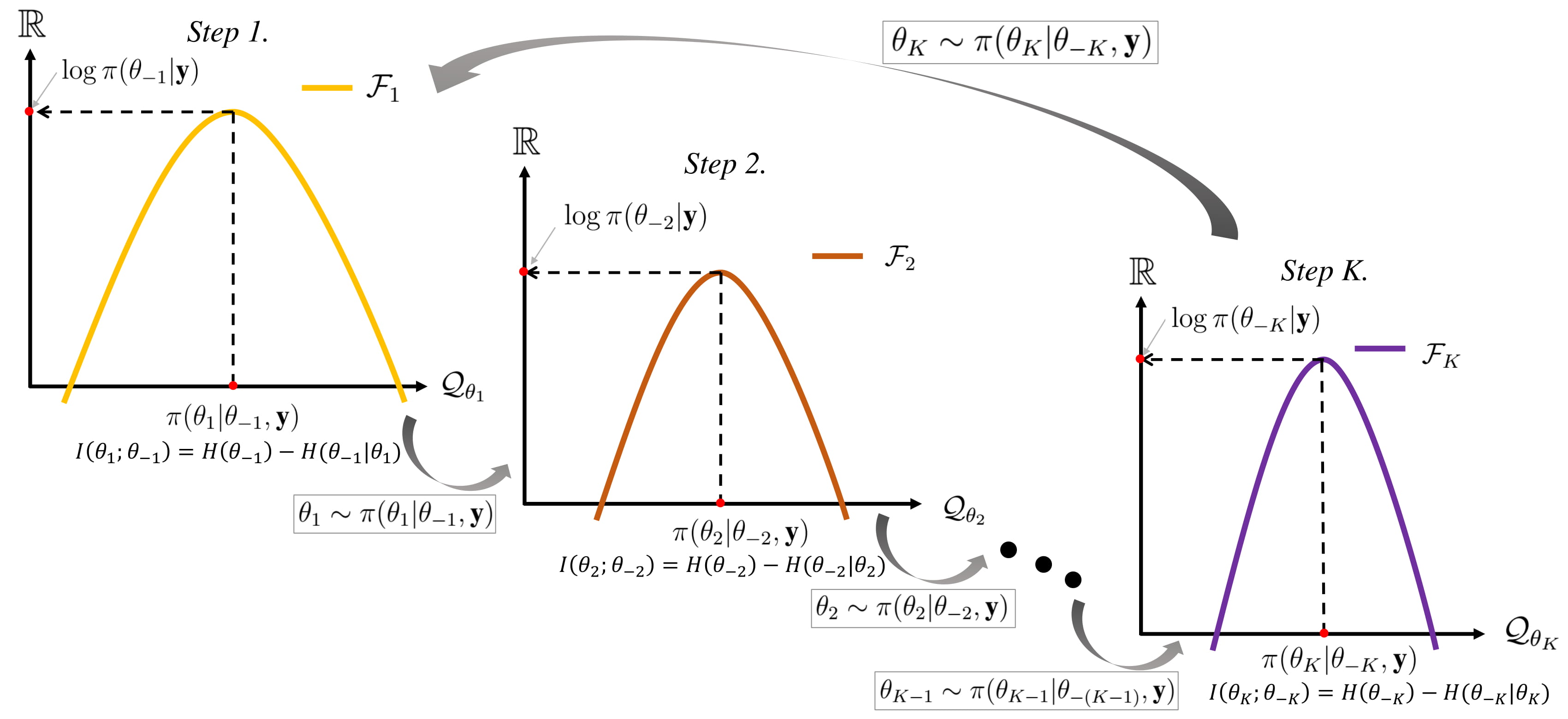
Now, for each , define the following information theoretic quantities:
namely, posterior mutual information, posterior differential entropy, and posterior conditional differential entropy, respectively. We can similarly define information theoretic quantities , , and by interchanging the and in the defined quantities. Then, the following equations hold.
.
The mutual information quantifies the reduction in uncertainty of random quantity once we know , a posteriori. It vanishes if and only if and are marginally independent, a posterior. The mutual information can be interpreted as the quantity that is transmitted from the -th step to the -th step within a single cycle of the Gibbs sampler.
The following algorithm details a generic Gibbs sampler:
Note that Gibbs sampler is operated by the iterative Monte Carlo scheme within a cycle. The number of samples drawn by the above algorithm formulates Markov Chains with the invariant distribution to be the target density .
Now, for each , define the following information theoretic quantities:
namely, posterior mutual information, posterior differential entropy, and posterior conditional differential entropy, respectively. We can similarly define information theoretic quantities , , and by interchanging the and in the defined quantities. Then, the following equations hold.
.
The mutual information quantifies the reduction in uncertainty of random quantity once we know , a posteriori. It vanishes if and only if and are marginally independent, a posterior. The mutual information can be interpreted as the quantity that is transmitted from the -th step to the -th step within a single cycle of the Gibbs sampler.
Turing
is an open source
Markov chain Monte Carlo
In statistics, Markov chain Monte Carlo (MCMC) methods comprise a class of algorithms for sampling from a probability distribution. By constructing a Markov chain that has the desired distribution as its equilibrium distribution, one can obtain ...
(MCMC) algorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific problems or to perform a computation. Algorithms are used as specifications for performing ...
for obtaining a sequence of observations which are approximated from a specified multivariate probability distribution, when direct sampling is difficult. This sequence can be used to approximate the joint distribution (e.g., to generate a histogram of the distribution); to approximate the marginal distribution of one of the variables, or some subset of the variables (for example, the unknown parameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when ...
s or latent variable
In statistics, latent variables (from Latin: present participle of ''lateo'', “lie hidden”) are variables that can only be inferred indirectly through a mathematical model from other observable variables that can be directly observed or me ...
s); or to compute an integral
In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along wit ...
(such as the expected value of one of the variables). Typically, some of the variables correspond to observations whose values are known, and hence do not need to be sampled.
Gibbs sampling is commonly used as a means of statistical inference, especially Bayesian inference. It is a randomized algorithm (i.e. an algorithm that makes use of random numbers), and is an alternative to deterministic algorithm
In computer science, a deterministic algorithm is an algorithm that, given a particular input, will always produce the same output, with the underlying machine always passing through the same sequence of states. Deterministic algorithms are by far ...
s for statistical inference such as the expectation-maximization algorithm (EM).
As with other MCMC algorithms, Gibbs sampling generates a Markov chain of samples, each of which is correlated with nearby samples. As a result, care must be taken if independent samples are desired. Generally, samples from the beginning of the chain (the ''burn-in period'') may not accurately represent the desired distribution and are usually discarded.
Introduction
Gibbs sampling is named after the physicistJosiah Willard Gibbs
Josiah Willard Gibbs (; February 11, 1839 – April 28, 1903) was an American scientist who made significant theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in t ...
, in reference to an analogy between the sampling algorithm and statistical physics
Statistical physics is a branch of physics that evolved from a foundation of statistical mechanics, which uses methods of probability theory and statistics, and particularly the mathematical tools for dealing with large populations and approxim ...
. The algorithm was described by brothers Stuart and Donald Geman in 1984, some eight decades after the death of Gibbs.
In its basic version, Gibbs sampling is a special case of the Metropolis–Hastings algorithm. However, in its extended versions (see below), it can be considered a general framework for sampling from a large set of variables by sampling each variable (or in some cases, each group of variables) in turn, and can incorporate the Metropolis–Hastings algorithm (or methods such as slice sampling
Slice sampling is a type of Markov chain Monte Carlo algorithm for pseudo-random number sampling, i.e. for drawing random samples from a statistical distribution. The method is based on the observation that to sample a random variable one can sampl ...
) to implement one or more of the sampling steps.
Gibbs sampling is applicable when the joint distribution is not known explicitly or is difficult to sample from directly, but the conditional distribution of each variable is known and is easy (or at least, easier) to sample from. The Gibbs sampling algorithm generates an instance from the distribution of each variable in turn, conditional on the current values of the other variables. It can be shown that the sequence of samples constitutes a Markov chain, and the stationary distribution of that Markov chain is just the sought-after joint distribution.
Gibbs sampling is particularly well-adapted to sampling the posterior distribution
The posterior probability is a type of conditional probability that results from updating the prior probability with information summarized by the likelihood via an application of Bayes' rule. From an epistemological perspective, the posterior p ...
of a Bayesian network
A Bayesian network (also known as a Bayes network, Bayes net, belief network, or decision network) is a probabilistic graphical model that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG). Bay ...
, since Bayesian networks are typically specified as a collection of conditional distributions.
Implementation
Gibbs sampling, in its basic incarnation, is a special case of the Metropolis–Hastings algorithm. The point of Gibbs sampling is that given amultivariate distribution
Given two random variables that are defined on the same probability space, the joint probability distribution is the corresponding probability distribution on all possible pairs of outputs. The joint distribution can just as well be considered ...
it is simpler to sample from a conditional distribution than to marginalize by integrating over a joint distribution
Given two random variables that are defined on the same probability space, the joint probability distribution is the corresponding probability distribution on all possible pairs of outputs. The joint distribution can just as well be considered ...
. Suppose we want to obtain samples of from a joint distribution . Denote the th sample by . We proceed as follows:
#We begin with some initial value .
#We want the next sample. Call this next sample . Since is a vector, we sample each component of the vector, , from the distribution of that component conditioned on all other components sampled so far. But there is a catch: we condition on 's components ''up to'' , and thereafter condition on 's components, starting from to . To achieve this, we sample the components in order, starting from the first component. More formally, to sample , we update it according to the distribution specified by . We use the value that the th component had in the th sample, not the th sample.
#Repeat the above step times.
If such sampling is performed, these important facts hold:
* The samples approximate the joint distribution of all variables.
* The marginal distribution of any subset of variables can be approximated by simply considering the samples for that subset of variables, ignoring the rest.
* The expected value of any variable can be approximated by averaging over all the samples.
When performing the sampling:
*The initial values of the variables can be determined randomly or by some other algorithm such as expectation-maximization.
*It is not actually necessary to determine an initial value for the first variable sampled.
*It is common to ignore some number of samples at the beginning (the so-called ''burn-in period''), and then consider only every th sample when averaging values to compute an expectation. For example, the first 1,000 samples might be ignored, and then every 100th sample averaged, throwing away all the rest. The reason for this is that (1) the stationary distribution Stationary distribution may refer to:
* A special distribution for a Markov chain such that if the chain starts with its stationary distribution, the marginal distribution of all states at any time will always be the stationary distribution. Assum ...
of the Markov chain is the desired joint distribution over the variables, but it may take a while for that stationary distribution to be reached; (2) successive samples are not independent of each other but form a Markov chain with some amount of correlation. Sometimes, algorithms can be used to determine the amount of autocorrelation between samples and the value of (the period between samples that are actually used) computed from this, but in practice there is a fair amount of "black magic
Black magic, also known as dark magic, has traditionally referred to the use of supernatural powers or magic for evil and selfish purposes, specifically the seven magical arts prohibited by canon law, as expounded by Johannes Hartlieb in 14 ...
" involved.
*The process of simulated annealing
Simulated annealing (SA) is a probabilistic technique for approximating the global optimum of a given function. Specifically, it is a metaheuristic to approximate global optimization in a large search space for an optimization problem. ...
is often used to reduce the "random walk
In mathematics, a random walk is a random process that describes a path that consists of a succession of random steps on some mathematical space.
An elementary example of a random walk is the random walk on the integer number line \mathbb Z ...
" behavior in the early part of the sampling process (i.e. the tendency to move slowly around the sample space, with a high amount of autocorrelation between samples, rather than moving around quickly, as is desired). Other techniques that may reduce autocorrelation are ''collapsed Gibbs sampling'', ''blocked Gibbs sampling'', and ''ordered overrelaxation''; see below.
Relation of conditional distribution and joint distribution
Furthermore, the conditional distribution of one variable given all others is proportional to the joint distribution: : "Proportional to" in this case means that the denominator is not a function of and thus is the same for all values of ; it forms part of thenormalization constant
The concept of a normalizing constant arises in probability theory and a variety of other areas of mathematics. The normalizing constant is used to reduce any probability function to a probability density function with total probability of one.
...
for the distribution over . In practice, to determine the nature of the conditional distribution of a factor , it is easiest to factor the joint distribution according to the individual conditional distributions defined by the graphical model
A graphical model or probabilistic graphical model (PGM) or structured probabilistic model is a probabilistic model for which a graph expresses the conditional dependence structure between random variables. They are commonly used in probabili ...
over the variables, ignore all factors that are not functions of (all of which, together with the denominator above, constitute the normalization constant), and then reinstate the normalization constant at the end, as necessary. In practice, this means doing one of three things:
#If the distribution is discrete, the individual probabilities of all possible values of are computed, and then summed to find the normalization constant.
#If the distribution is continuous and of a known form, the normalization constant will also be known.
#In other cases, the normalization constant can usually be ignored, as most sampling methods do not require it.
Inference
Gibbs sampling is commonly used for statistical inference (e.g. determining the best value of a parameter, such as determining the number of people likely to shop at a particular store on a given day, the candidate a voter will most likely vote for, etc.). The idea is that observed data is incorporated into the sampling process by creating separate variables for each piece of observed data and fixing the variables in question to their observed values, rather than sampling from those variables. The distribution of the remaining variables is then effectively aposterior distribution
The posterior probability is a type of conditional probability that results from updating the prior probability with information summarized by the likelihood via an application of Bayes' rule. From an epistemological perspective, the posterior p ...
conditioned on the observed data.
The most likely value of a desired parameter (the mode
Mode ( la, modus meaning "manner, tune, measure, due measure, rhythm, melody") may refer to:
Arts and entertainment
* '' MO''D''E (magazine)'', a defunct U.S. women's fashion magazine
* ''Mode'' magazine, a fictional fashion magazine which is ...
) could then simply be selected by choosing the sample value that occurs most commonly; this is essentially equivalent to maximum a posteriori
In Bayesian statistics, a maximum a posteriori probability (MAP) estimate is an estimate of an unknown quantity, that equals the mode of the posterior distribution. The MAP can be used to obtain a point estimate of an unobserved quantity on the ...
estimation of a parameter. (Since the parameters are usually continuous, it is often necessary to "bin" the sampled values into one of a finite number of ranges or "bins" in order to get a meaningful estimate of the mode.) More commonly, however, the expected value (mean
There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value (magnitude and sign) of a given data set.
For a data set, the '' ari ...
or average) of the sampled values is chosen; this is a Bayes estimator that takes advantage of the additional data about the entire distribution that is available from Bayesian sampling, whereas a maximization algorithm such as expectation maximization
Expectation or Expectations may refer to:
Science
* Expectation (epistemic)
* Expected value, in mathematical probability theory
* Expectation value (quantum mechanics)
* Expectation–maximization algorithm, in statistics
Music
* ''Expectati ...
(EM) is capable of only returning a single point from the distribution. For example, for a unimodal distribution the mean (expected value) is usually similar to the mode (most common value), but if the distribution is skewed
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined.
For a unimoda ...
in one direction, the mean will be moved in that direction, which effectively accounts for the extra probability mass in that direction. (If a distribution is multimodal, the expected value may not return a meaningful point, and any of the modes is typically a better choice.)
Although some of the variables typically correspond to parameters of interest, others are uninteresting ("nuisance") variables introduced into the model to properly express the relationships among variables. Although the sampled values represent the joint distribution
Given two random variables that are defined on the same probability space, the joint probability distribution is the corresponding probability distribution on all possible pairs of outputs. The joint distribution can just as well be considered ...
over all variables, the nuisance variables can simply be ignored when computing expected values or modes; this is equivalent to marginalizing over the nuisance variables. When a value for multiple variables is desired, the expected value is simply computed over each variable separately. (When computing the mode, however, all variables must be considered together.)
Supervised learning
Supervised learning (SL) is a machine learning paradigm for problems where the available data consists of labelled examples, meaning that each data point contains features (covariates) and an associated label. The goal of supervised learning alg ...
, unsupervised learning
Unsupervised learning is a type of algorithm that learns patterns from untagged data. The hope is that through mimicry, which is an important mode of learning in people, the machine is forced to build a concise representation of its world and t ...
and semi-supervised learning Weak supervision is a branch of machine learning where noisy, limited, or imprecise sources are used to provide supervision signal for labeling large amounts of training data in a supervised learning setting. This approach alleviates the burden of ...
(aka learning with missing values) can all be handled by simply fixing the values of all variables whose values are known, and sampling from the remainder.
For observed data, there will be one variable for each observation—rather than, for example, one variable corresponding to the sample mean
The sample mean (or "empirical mean") and the sample covariance are statistics computed from a sample of data on one or more random variables.
The sample mean is the average value (or mean value) of a sample of numbers taken from a larger popu ...
or sample variance
In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its population mean or sample mean. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbe ...
of a set of observations. In fact, there generally will be no variables at all corresponding to concepts such as "sample mean" or "sample variance". Instead, in such a case there will be variables representing the unknown true mean and true variance, and the determination of sample values for these variables results automatically from the operation of the Gibbs sampler.
Generalized linear models (i.e. variations of linear regression) can sometimes be handled by Gibbs sampling as well. For example, probit regression
In statistics, a probit model is a type of regression where the dependent variable can take only two values, for example married or not married. The word is a portmanteau, coming from ''probability'' + ''unit''. The purpose of the model is to e ...
for determining the probability of a given binary (yes/no) choice, with normally distributed priors placed over the regression coefficients, can be implemented with Gibbs sampling because it is possible to add additional variables and take advantage of conjugacy. However, logistic regression
In statistics, the logistic model (or logit model) is a statistical model that models the probability of an event taking place by having the log-odds for the event be a linear combination of one or more independent variables. In regression a ...
cannot be handled this way. One possibility is to approximate the logistic function with a mixture (typically 7–9) of normal distributions. More commonly, however, Metropolis–Hastings is used instead of Gibbs sampling.
Mathematical background
Suppose that a sample is taken from a distribution depending on a parameter vector of length , with prior distribution . It may be that is very large and that numerical integration to find the marginal densities of the would be computationally expensive. Then an alternative method of calculating the marginal densities is to create a Markov chain on the space by repeating these two steps: # Pick a random index # Pick a new value for according to These steps define a reversible Markov chain with the desired invariant distribution . This can be proved as follows. Define if for all and let denote the probability of a jump from to . Then, the transition probabilities are : So : since is an equivalence relation. Thus the detailed balance equations are satisfied, implying the chain is reversible and it has invariant distribution . In practice, the index is not chosen at random, and the chain cycles through the indexes in order. In general this gives a non-stationary Markov process, but each individual step will still be reversible, and the overall process will still have the desired stationary distribution (as long as the chain can access all states under the fixed ordering).Gibbs sampler in Bayesian inference and its relation to information theory
Let denote observations generated from the sampling distribution and be a prior supported on the parameter space . Then one of the central goals of theBayesian statistics
Bayesian statistics is a theory in the field of statistics based on the Bayesian interpretation of probability where probability expresses a ''degree of belief'' in an event. The degree of belief may be based on prior knowledge about the event, ...
is to approximate the posterior density
:
where the marginal likelihood is assumed to be finite for all .
To explain the Gibbs sampler, we additionally assume that the parameter space is decomposed as
:,
where represents the Cartesian product. Each component parameter space can be a set of scalar components, subvectors, or matrices.
Define a set that complements the . Essential ingredients of the Gibbs sampler is the -th full conditional posterior distribution for each
:.

 The following algorithm details a generic Gibbs sampler:
Note that Gibbs sampler is operated by the iterative Monte Carlo scheme within a cycle. The number of samples drawn by the above algorithm formulates Markov Chains with the invariant distribution to be the target density .
Now, for each , define the following information theoretic quantities:
namely, posterior mutual information, posterior differential entropy, and posterior conditional differential entropy, respectively. We can similarly define information theoretic quantities , , and by interchanging the and in the defined quantities. Then, the following equations hold.
.
The mutual information quantifies the reduction in uncertainty of random quantity once we know , a posteriori. It vanishes if and only if and are marginally independent, a posterior. The mutual information can be interpreted as the quantity that is transmitted from the -th step to the -th step within a single cycle of the Gibbs sampler.
The following algorithm details a generic Gibbs sampler:
Note that Gibbs sampler is operated by the iterative Monte Carlo scheme within a cycle. The number of samples drawn by the above algorithm formulates Markov Chains with the invariant distribution to be the target density .
Now, for each , define the following information theoretic quantities:
namely, posterior mutual information, posterior differential entropy, and posterior conditional differential entropy, respectively. We can similarly define information theoretic quantities , , and by interchanging the and in the defined quantities. Then, the following equations hold.
.
The mutual information quantifies the reduction in uncertainty of random quantity once we know , a posteriori. It vanishes if and only if and are marginally independent, a posterior. The mutual information can be interpreted as the quantity that is transmitted from the -th step to the -th step within a single cycle of the Gibbs sampler.
Variations and extensions
Numerous variations of the basic Gibbs sampler exist. The goal of these variations is to reduce the autocorrelation between samples sufficiently to overcome any added computational costs.Blocked Gibbs sampler
*A blocked Gibbs sampler groups two or more variables together and samples from theirjoint distribution
Given two random variables that are defined on the same probability space, the joint probability distribution is the corresponding probability distribution on all possible pairs of outputs. The joint distribution can just as well be considered ...
conditioned on all other variables, rather than sampling from each one individually. For example, in a hidden Markov model
A hidden Markov model (HMM) is a statistical Markov model in which the system being modeled is assumed to be a Markov process — call it X — with unobservable ("''hidden''") states. As part of the definition, HMM requires that there be an o ...
, a blocked Gibbs sampler might sample from all the latent variable
In statistics, latent variables (from Latin: present participle of ''lateo'', “lie hidden”) are variables that can only be inferred indirectly through a mathematical model from other observable variables that can be directly observed or me ...
s making up the Markov chain in one go, using the forward-backward algorithm.
Collapsed Gibbs sampler
*A collapsed Gibbs sampler integrates out ( marginalizes over) one or more variables when sampling for some other variable. For example, imagine that a model consists of three variables ''A'', ''B'', and ''C''. A simple Gibbs sampler would sample from ''p''(''A'' , ''B'',''C''), then ''p''(''B'' , ''A'',''C''), then ''p''(''C'' , ''A'',''B''). A collapsed Gibbs sampler might replace the sampling step for ''A'' with a sample taken from the marginal distribution ''p''(''A'' , ''C''), with variable ''B'' integrated out in this case. Alternatively, variable ''B'' could be collapsed out entirely, alternately sampling from ''p''(''A'' , ''C'') and ''p''(''C'' , ''A'') and not sampling over ''B'' at all. The distribution over a variable ''A'' that arises when collapsing a parent variable ''B'' is called acompound distribution In probability and statistics, a compound probability distribution (also known as a mixture distribution or contagious distribution) is the probability distribution that results from assuming that a random variable is distributed according to som ...
; sampling from this distribution is generally tractable when ''B'' is the conjugate prior
In Bayesian probability theory, if the posterior distribution p(\theta \mid x) is in the same probability distribution family as the prior probability distribution p(\theta), the prior and posterior are then called conjugate distributions, and th ...
for ''A'', particularly when ''A'' and ''B'' are members of the exponential family
In probability and statistics, an exponential family is a parametric set of probability distributions of a certain form, specified below. This special form is chosen for mathematical convenience, including the enabling of the user to calculate ...
. For more information, see the article on compound distribution In probability and statistics, a compound probability distribution (also known as a mixture distribution or contagious distribution) is the probability distribution that results from assuming that a random variable is distributed according to som ...
s or Liu (1994).
Implementing a collapsed Gibbs sampler
= Collapsing Dirichlet distributions
= Inhierarchical Bayesian model
A Bayesian network (also known as a Bayes network, Bayes net, belief network, or decision network) is a probabilistic graphical model that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG). Bay ...
s with categorical variables, such as latent Dirichlet allocation
In natural language processing, Latent Dirichlet Allocation (LDA) is a generative statistical model that explains a set of observations through unobserved groups, and each group explains why some parts of the data are similar. The LDA is an ex ...
and various other models used in natural language processing, it is quite common to collapse out the Dirichlet distribution
In probability and statistics, the Dirichlet distribution (after Peter Gustav Lejeune Dirichlet), often denoted \operatorname(\boldsymbol\alpha), is a family of continuous multivariate probability distributions parameterized by a vector \bold ...
s that are typically used as prior distribution
In Bayesian statistical inference, a prior probability distribution, often simply called the prior, of an uncertain quantity is the probability distribution that would express one's beliefs about this quantity before some evidence is taken int ...
s over the categorical variables. The result of this collapsing introduces dependencies among all the categorical variables dependent on a given Dirichlet prior, and the joint distribution of these variables after collapsing is a Dirichlet-multinomial distribution
In probability theory and statistics, the Dirichlet-multinomial distribution is a family of discrete multivariate probability distributions on a finite support of non-negative integers. It is also called the Dirichlet compound multinomial distribut ...
. The conditional distribution of a given categorical variable in this distribution, conditioned on the others, assumes an extremely simple form that makes Gibbs sampling even easier than if the collapsing had not been done. The rules are as follows:
#Collapsing out a Dirichlet prior node affects only the parent and children nodes of the prior. Since the parent is often a constant, it is typically only the children that we need to worry about.
#Collapsing out a Dirichlet prior introduces dependencies among all the categorical children dependent on that prior — but ''no'' extra dependencies among any other categorical children. (This is important to keep in mind, for example, when there are multiple Dirichlet priors related by the same hyperprior. Each Dirichlet prior can be independently collapsed and affects only its direct children.)
#After collapsing, the conditional distribution of one dependent children on the others assumes a very simple form: The probability of seeing a given value is proportional to the sum of the corresponding hyperprior for this value, and the count of all of the ''other dependent nodes'' assuming the same value. Nodes not dependent on the same prior must not be counted. The same rule applies in other iterative inference methods, such as variational Bayes
Variational Bayesian methods are a family of techniques for approximating intractable integrals arising in Bayesian inference and machine learning. They are typically used in complex statistical models consisting of observed variables (usuall ...
or expectation maximization
Expectation or Expectations may refer to:
Science
* Expectation (epistemic)
* Expected value, in mathematical probability theory
* Expectation value (quantum mechanics)
* Expectation–maximization algorithm, in statistics
Music
* ''Expectati ...
; however, if the method involves keeping partial counts, then the partial counts for the value in question must be summed across all the other dependent nodes. Sometimes this summed up partial count is termed the ''expected count'' or similar. The probability is ''proportional to'' the resulting value; the actual probability must be determined by normalizing across all the possible values that the categorical variable can take (i.e. adding up the computed result for each possible value of the categorical variable, and dividing all the computed results by this sum).
#If a given categorical node has dependent children (e.g. when it is a latent variable
In statistics, latent variables (from Latin: present participle of ''lateo'', “lie hidden”) are variables that can only be inferred indirectly through a mathematical model from other observable variables that can be directly observed or me ...
in a mixture model
In statistics, a mixture model is a probabilistic model for representing the presence of subpopulations within an overall population, without requiring that an observed data set should identify the sub-population to which an individual observatio ...
), the value computed in the previous step (expected count plus prior, or whatever is computed) must be multiplied by the actual conditional probabilities (''not'' a computed value that is proportional to the probability!) of all children given their parents. See the article on the Dirichlet-multinomial distribution
In probability theory and statistics, the Dirichlet-multinomial distribution is a family of discrete multivariate probability distributions on a finite support of non-negative integers. It is also called the Dirichlet compound multinomial distribut ...
for a detailed discussion.
#In the case where the group membership of the nodes dependent on a given Dirichlet prior may change dynamically depending on some other variable (e.g. a categorical variable indexed by another latent categorical variable, as in a topic model
In statistics and natural language processing, a topic model is a type of statistical model for discovering the abstract "topics" that occur in a collection of documents. Topic modeling is a frequently used text-mining tool for discovery of hidden ...
), the same expected counts are still computed, but need to be done carefully so that the correct set of variables is included. See the article on the Dirichlet-multinomial distribution
In probability theory and statistics, the Dirichlet-multinomial distribution is a family of discrete multivariate probability distributions on a finite support of non-negative integers. It is also called the Dirichlet compound multinomial distribut ...
for more discussion, including in the context of a topic model.
= Collapsing other conjugate priors
= In general, any conjugate prior can be collapsed out, if its only children have distributions conjugate to it. The relevant math is discussed in the article oncompound distribution In probability and statistics, a compound probability distribution (also known as a mixture distribution or contagious distribution) is the probability distribution that results from assuming that a random variable is distributed according to som ...
s. If there is only one child node, the result will often assume a known distribution. For example, collapsing an inverse-gamma-distributed variance
In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its population mean or sample mean. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbe ...
out of a network with a single Gaussian
Carl Friedrich Gauss (1777–1855) is the eponym of all of the topics listed below.
There are over 100 topics all named after this German mathematician and scientist, all in the fields of mathematics, physics, and astronomy. The English eponymo ...
child will yield a Student's t-distribution. (For that matter, collapsing both the mean and variance of a single Gaussian child will still yield a Student's t-distribution, provided both are conjugate, i.e. Gaussian mean, inverse-gamma variance.)
If there are multiple child nodes, they will all become dependent, as in the Dirichlet
Johann Peter Gustav Lejeune Dirichlet (; 13 February 1805 – 5 May 1859) was a German mathematician who made deep contributions to number theory (including creating the field of analytic number theory), and to the theory of Fourier series and ...
- categorical case. The resulting joint distribution
Given two random variables that are defined on the same probability space, the joint probability distribution is the corresponding probability distribution on all possible pairs of outputs. The joint distribution can just as well be considered ...
will have a closed form that resembles in some ways the compound distribution, although it will have a product of a number of factors, one for each child node, in it.
In addition, and most importantly, the resulting conditional distribution of one of the child nodes given the others (and also given the parents of the collapsed node(s), but ''not'' given the children of the child nodes) will have the same density as the posterior predictive distribution of all the remaining child nodes. Furthermore, the posterior predictive distribution has the same density as the basic compound distribution of a single node, although with different parameters. The general formula is given in the article on compound distribution In probability and statistics, a compound probability distribution (also known as a mixture distribution or contagious distribution) is the probability distribution that results from assuming that a random variable is distributed according to som ...
s.
For example, given a Bayes network with a set of conditionally independent identically distributed
In probability theory and statistics, a collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent. This property is us ...
Gaussian-distributed nodes with conjugate prior
In Bayesian probability theory, if the posterior distribution p(\theta \mid x) is in the same probability distribution family as the prior probability distribution p(\theta), the prior and posterior are then called conjugate distributions, and th ...
distributions placed on the mean and variance, the conditional distribution of one node given the others after compounding out both the mean and variance will be a Student's t-distribution. Similarly, the result of compounding out the gamma prior of a number of Poisson-distributed nodes causes the conditional distribution of one node given the others to assume a negative binomial distribution.
In these cases where compounding produces a well-known distribution, efficient sampling procedures often exist, and using them will often (although not necessarily) be more efficient than not collapsing, and instead sampling both prior and child nodes separately. However, in the case where the compound distribution is not well-known, it may not be easy to sample from, since it generally will not belong to the exponential family
In probability and statistics, an exponential family is a parametric set of probability distributions of a certain form, specified below. This special form is chosen for mathematical convenience, including the enabling of the user to calculate ...
and typically will not be log-concave (which would make it easy to sample using adaptive rejection sampling
In numerical analysis and computational statistics, rejection sampling is a basic technique used to generate observations from a distribution. It is also commonly called the acceptance-rejection method or "accept-reject algorithm" and is a type of ...
, since a closed form always exists).
In the case where the child nodes of the collapsed nodes themselves have children, the conditional distribution of one of these child nodes given all other nodes in the graph will have to take into account the distribution of these second-level children. In particular, the resulting conditional distribution will be proportional to a product of the compound distribution as defined above, and the conditional distributions of all of the child nodes given their parents (but not given their own children). This follows from the fact that the full conditional distribution is proportional to the joint distribution. If the child nodes of the collapsed nodes are continuous
Continuity or continuous may refer to:
Mathematics
* Continuity (mathematics), the opposing concept to discreteness; common examples include
** Continuous probability distribution or random variable in probability and statistics
** Continuous ...
, this distribution will generally not be of a known form, and may well be difficult to sample from despite the fact that a closed form can be written, for the same reasons as described above for non-well-known compound distributions. However, in the particular case that the child nodes are discrete
Discrete may refer to:
*Discrete particle or quantum in physics, for example in quantum theory
*Discrete device, an electronic component with just one circuit element, either passive or active, other than an integrated circuit
*Discrete group, a g ...
, sampling is feasible, regardless of whether the children of these child nodes are continuous or discrete. In fact, the principle involved here is described in fair detail in the article on the Dirichlet-multinomial distribution
In probability theory and statistics, the Dirichlet-multinomial distribution is a family of discrete multivariate probability distributions on a finite support of non-negative integers. It is also called the Dirichlet compound multinomial distribut ...
.
Gibbs sampler with ordered overrelaxation
*A Gibbs sampler with ordered overrelaxation samples a given odd number of candidate values for at any given step and sorts them, along with the single value for according to some well-defined ordering. If is the ''s''th smallest in the sorted list then the is selected as the ''s''th largest in the sorted list. For more information, see Neal (1995).Other extensions
It is also possible to extend Gibbs sampling in various ways. For example, in the case of variables whose conditional distribution is not easy to sample from, a single iteration ofslice sampling
Slice sampling is a type of Markov chain Monte Carlo algorithm for pseudo-random number sampling, i.e. for drawing random samples from a statistical distribution. The method is based on the observation that to sample a random variable one can sampl ...
or the Metropolis–Hastings algorithm can be used to sample from the variables in question.
It is also possible to incorporate variables that are not random variables, but whose value is deterministically computed from other variables. Generalized linear models, e.g. logistic regression
In statistics, the logistic model (or logit model) is a statistical model that models the probability of an event taking place by having the log-odds for the event be a linear combination of one or more independent variables. In regression a ...
(aka " maximum entropy models"), can be incorporated in this fashion. (BUGS, for example, allows this type of mixing of models.)
Failure modes
There are two ways that Gibbs sampling can fail. The first is when there are islands of high-probability states, with no paths between them. For example, consider a probability distribution over 2-bit vectors, where the vectors (0,0) and (1,1) each have probability ½, but the other two vectors (0,1) and (1,0) have probability zero. Gibbs sampling will become trapped in one of the two high-probability vectors, and will never reach the other one. More generally, for any distribution over high-dimensional, real-valued vectors, if two particular elements of the vector are perfectly correlated (or perfectly anti-correlated), those two elements will become stuck, and Gibbs sampling will never be able to change them. The second problem can happen even when all states have nonzero probability and there is only a single island of high-probability states. For example, consider a probability distribution over 100-bit vectors, where the all-zeros vector occurs with probability ½, and all other vectors are equally probable, and so have a probability of each. If you want to estimate the probability of the zero vector, it would be sufficient to take 100 or 1000 samples from the true distribution. That would very likely give an answer very close to ½. But you would probably have to take more than samples from Gibbs sampling to get the same result. No computer could do this in a lifetime. This problem occurs no matter how long the burn-in period is. This is because in the true distribution, the zero vector occurs half the time, and those occurrences are randomly mixed in with the nonzero vectors. Even a small sample will see both zero and nonzero vectors. But Gibbs sampling will alternate between returning only the zero vector for long periods (about in a row), then only nonzero vectors for long periods (about in a row). Thus convergence to the true distribution is extremely slow, requiring much more than steps; taking this many steps is not computationally feasible in a reasonable time period. The slow convergence here can be seen as a consequence of thecurse of dimensionality
The curse of dimensionality refers to various phenomena that arise when analyzing and organizing data in high-dimensional spaces that do not occur in low-dimensional settings such as the three-dimensional physical space of everyday experience. T ...
.
A problem like this can be solved by block sampling the entire 100-bit vector at once. (This assumes that the 100-bit vector is part of a larger set of variables. If this vector is the only thing being sampled, then block sampling is equivalent to not doing Gibbs sampling at all, which by hypothesis would be difficult.)Software
* TheOpenBUGS
OpenBUGS is a software application for the Bayesian analysis of complex statistical models using Markov chain Monte Carlo (MCMC) methods. OpenBUGS is the open source variant of WinBUGS ( Bayesian inference Using Gibbs Sampling). It runs under ...
software (''Bayesian inference Using Gibbs Sampling'') does a Bayesian analysis
Bayesian inference is a method of statistical inference in which Bayes' theorem is used to update the probability for a hypothesis as more evidence or information becomes available. Bayesian inference is an important technique in statistics, and e ...
of complex statistical models using Markov chain Monte Carlo
In statistics, Markov chain Monte Carlo (MCMC) methods comprise a class of algorithms for sampling from a probability distribution. By constructing a Markov chain that has the desired distribution as its equilibrium distribution, one can obtain ...
.
* JAGS (''Just another Gibbs sampler'') is a GPL program for analysis of Bayesian hierarchical models using Markov Chain Monte Carlo.
* Church
Church may refer to:
Religion
* Church (building), a building for Christian religious activities
* Church (congregation), a local congregation of a Christian denomination
* Church service, a formalized period of Christian communal worship
* C ...
is free software for performing Gibbs inference over arbitrary distributions that are specified as probabilistic programs.
* PyMC is an open source Python
Python may refer to:
Snakes
* Pythonidae, a family of nonvenomous snakes found in Africa, Asia, and Australia
** ''Python'' (genus), a genus of Pythonidae found in Africa and Asia
* Python (mythology), a mythical serpent
Computing
* Python (pro ...
library for Bayesian learning
Bayesian inference is a method of statistical inference in which Bayes' theorem is used to update the probability for a hypothesis as more evidence or information becomes available. Bayesian inference is an important technique in statistics, and e ...
of general Probabilistic Graphical Models.Turing
is an open source
Julia
Julia is usually a feminine given name. It is a Latinate feminine form of the name Julio and Julius. (For further details on etymology, see the Wiktionary entry "Julius".) The given name ''Julia'' had been in use throughout Late Antiquity (e.g ...
library for Bayesian Inference using probabilistic programming
Probabilistic programming (PP) is a programming paradigm in which probabilistic models are specified and inference for these models is performed automatically.
It represents an attempt to unify probabilistic modeling and traditional general pur ...
.
Notes
References
* * Bolstad, William M. (2010), ''Understanding Computational Bayesian Statistics'', John Wiley * (Contains a basic summary and many references.) * {{Citation , first1=Alan E. , last1=Gelfand , first2=Adrian F. M. , last2=Smith , title=Sampling-Based Approaches to Calculating Marginal Densities , journal=Journal of the American Statistical Association
The ''Journal of the American Statistical Association (JASA)'' is the primary journal published by the American Statistical Association, the main professional body for statisticians in the United States. It is published four times a year in Mar ...
, volume=85 , issue=410 , pages=398–409 , year=1990
, mr=1141740 , doi=10.2307/2289776
, jstor=2289776
* Gelman, A., Carlin J. B., Stern H. S., Dunson D., Vehtari A., Rubin D. B. (2013), ''Bayesian Data Analysis'', third edition. London: Chapman & Hall
Chapman & Hall is an Imprint (trade name), imprint owned by CRC Press, originally founded as a United Kingdom, British publishing house in London in the first half of the 19th century by Edward Chapman (publisher), Edward Chapman and William Hall ...
.
* Levin, David A.; Peres, Yuval; Wilmer, Elizabeth L. (2008), "Markov Chains and Mixing Times
''Markov Chains and Mixing Times'' is a book on Markov chain mixing times. The second edition was written by David A. Levin, and Yuval Peres. Elizabeth Wilmer was a co-author on the first edition and is credited as a contributor to the second edi ...
", American Mathematical Society
The American Mathematical Society (AMS) is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, and serves the national and international community through its publications, meetings, ...
.
* Robert, C. P.; Casella, G. (2004), ''Monte Carlo Statistical Methods'' (second edition), Springer-Verlag.
Markov chain Monte Carlo