Geometric group theory is an area in

mathematics Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...

devoted to the study of

finitely generated group In algebra, a finitely generated group is a group ''G'' that has some finite generating set ''S'' so that every element of ''G'' can be written as the combination (under the group operation) of finitely many elements of ''S'' and of inverses o ...

s via exploring the connections between

algebra Algebra () is one of the broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics. Elementary ...

ic properties of such

groups A group is a number of persons or things that are located, gathered, or classed together. Groups of people * Cultural group, a group whose members share the same cultural identity * Ethnic group, a group whose members share the same ethnic ide ...

and

topological In mathematics, topology (from the Greek words , and ) is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing ...

and

geometric Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is ca ...

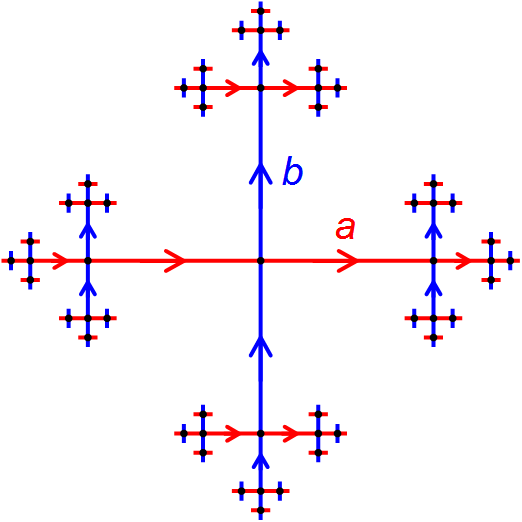
properties of spaces on which these groups act (that is, when the groups in question are realized as geometric symmetries or continuous transformations of some spaces). Another important idea in geometric group theory is to consider finitely generated groups themselves as geometric objects. This is usually done by studying the

Cayley graph In mathematics, a Cayley graph, also known as a Cayley color graph, Cayley diagram, group diagram, or color group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem (named after Arthur Cay ...

s of groups, which, in addition to the

graph Graph may refer to: Mathematics *Graph (discrete mathematics), a structure made of vertices and edges **Graph theory, the study of such graphs and their properties *Graph (topology), a topological space resembling a graph in the sense of discre ...

structure, are endowed with the structure of a

metric space In mathematics, a metric space is a set together with a notion of '' distance'' between its elements, usually called points. The distance is measured by a function called a metric or distance function. Metric spaces are the most general setti ...

, given by the so-called

word metric In group theory, a word metric on a discrete group G is a way to measure distance between any two elements of G . As the name suggests, the word metric is a metric on G , assigning to any two elements g , h of G a distance d(g,h) that m ...

. Geometric group theory, as a distinct area, is relatively new, and became a clearly identifiable branch of mathematics in the late 1980s and early 1990s. Geometric group theory closely interacts with

low-dimensional topology In mathematics, low-dimensional topology is the branch of topology that studies manifolds, or more generally topological spaces, of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot th ...

hyperbolic geometry In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai–Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with: :For any given line ''R'' and point ''P ...

algebraic topology Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify ...

computational group theory In mathematics, computational group theory is the study of groups by means of computers. It is concerned with designing and analysing algorithms and data structures to compute information about groups. The subject has attracted interest because f ...

and

differential geometry Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and mult ...

. There are also substantial connections with complexity theory,

mathematical logic Mathematical logic is the study of formal logic within mathematics. Major subareas include model theory, proof theory, set theory, and recursion theory. Research in mathematical logic commonly addresses the mathematical properties of forma ...

, the study of

Lie group In mathematics, a Lie group (pronounced ) is a group that is also a differentiable manifold. A manifold is a space that locally resembles Euclidean space, whereas groups define the abstract concept of a binary operation along with the addi ...

s and their discrete subgroups,

dynamical systems In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a ...

probability theory Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set ...

K-theory In mathematics, K-theory is, roughly speaking, the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is a cohomology theory known as topological K-theory. In algebra and algebraic geometr ...

, and other areas of mathematics. In the introduction to his book ''Topics in Geometric Group Theory'', Pierre de la Harpe wrote: "One of my personal beliefs is that fascination with symmetries and groups is one way of coping with frustrations of life's limitations: we like to recognize symmetries which allow us to recognize more than what we can see. In this sense the study of geometric group theory is a part of culture, and reminds me of several things that Georges de Rham practiced on many occasions, such as teaching mathematics, reciting Mallarmé, or greeting a friend".

History

Geometric group theory grew out of

combinatorial group theory In mathematics, combinatorial group theory is the theory of free groups, and the concept of a presentation of a group by generators and relations. It is much used in geometric topology, the fundamental group of a simplicial complex having in a nat ...

that largely studied properties of

discrete group In mathematics, a topological group ''G'' is called a discrete group if there is no limit point in it (i.e., for each element in ''G'', there is a neighborhood which only contains that element). Equivalently, the group ''G'' is discrete if and o ...

s via analyzing group presentations, that describe groups as quotients of

free group In mathematics, the free group ''F'S'' over a given set ''S'' consists of all words that can be built from members of ''S'', considering two words to be different unless their equality follows from the group axioms (e.g. ''st'' = ''suu''−1' ...

s; this field was first systematically studied by

Walther von Dyck Walther Franz Anton von Dyck (6 December 1856 – 5 November 1934), born Dyck () and later ennobled, was a German mathematician. He is credited with being the first to define a mathematical group, in the modern sense in . He laid the foundations ...

, student of

Felix Klein Christian Felix Klein (; 25 April 1849 – 22 June 1925) was a German mathematician and mathematics educator, known for his work with group theory, complex analysis, non-Euclidean geometry, and on the associations between geometry and grou ...

, in the early 1880s, while an early form is found in the 1856

icosian calculus The icosian calculus is a non-commutative algebraic structure discovered by the Irish mathematician William Rowan Hamilton in 1856. In modern terms, he gave a group presentation of the icosahedral rotation group by generators and relations. Ham ...

William Rowan Hamilton Sir William Rowan Hamilton Doctor of Law, LL.D, Doctor of Civil Law, DCL, Royal Irish Academy, MRIA, Royal Astronomical Society#Fellow, FRAS (3/4 August 1805 – 2 September 1865) was an Irish mathematician, astronomer, and physicist. He was the ...

, where he studied the

icosahedral symmetry In mathematics, and especially in geometry, an object has icosahedral symmetry if it has the same symmetries as a regular icosahedron. Examples of other polyhedra with icosahedral symmetry include the regular dodecahedron (the dual polyhedr ...

group via the edge graph of the

dodecahedron In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagon ...

. Currently combinatorial group theory as an area is largely subsumed by geometric group theory. Moreover, the term "geometric group theory" came to often include studying discrete groups using probabilistic, measure-theoretic, arithmetic, analytic and other approaches that lie outside of the traditional combinatorial group theory arsenal. In the first half of the 20th century, pioneering work of

Max Dehn Max Wilhelm Dehn (November 13, 1878 – June 27, 1952) was a German mathematician most famous for his work in geometry, topology and geometric group theory. Born to a Jewish family in Germany, Dehn's early life and career took place in Germany. ...

Jakob Nielsen Jacob or Jakob Nielsen may refer to: * Jacob Nielsen, Count of Halland (died c. 1309), great grandson of Valdemar II of Denmark * , Norway (1768-1822) * Jakob Nielsen (mathematician) (1890–1959), Danish mathematician known for work on automorphis ...

Kurt Reidemeister Kurt Werner Friedrich Reidemeister (13 October 1893 – 8 July 1971) was a mathematician born in Braunschweig (Brunswick), Germany. Life He was a brother of Marie Neurath. Beginning in 1912, he studied in Freiburg, Munich, Marburg, and G� ...

and Otto Schreier,

J. H. C. Whitehead John Henry Constantine Whitehead FRS (11 November 1904 – 8 May 1960), known as Henry, was a British mathematician and was one of the founders of homotopy theory. He was born in Chennai (then known as Madras), in India, and died in Princeton, ...

Egbert van Kampen Egbert Rudolf van Kampen (28 May 1908 – 11 February 1942) was a Dutch mathematician. He made important contributions to topology, especially to the study of fundamental groups. Life Van Kampen was born to Dutch parents in Belgium, wher ...

, amongst others, introduced some topological and geometric ideas into the study of discrete groups. Other precursors of geometric group theory include

small cancellation theory In the mathematical subject of group theory, small cancellation theory studies groups given by group presentations satisfying small cancellation conditions, that is where defining relations have "small overlaps" with each other. Small cancellation ...

and

Bass–Serre theory Bass–Serre theory is a part of the mathematical subject of group theory that deals with analyzing the algebraic structure of groups acting by automorphisms on simplicial trees. The theory relates group actions on trees with decomposing groups as i ...

. Small cancellation theory was introduced by Martin Grindlinger in the 1960s and further developed by

Roger Lyndon Roger Conant Lyndon (December 18, 1917 – June 8, 1988) was an American mathematician, for many years a professor at the University of Michigan.. He is known for Lyndon words, the Curtis–Hedlund–Lyndon theorem, Craig–Lyndon interpolation ...

and Paul Schupp. It studies

van Kampen diagram In the mathematical area of geometric group theory, a Van Kampen diagram (sometimes also called a Lyndon–Van Kampen diagram ) is a planar diagram used to represent the fact that a particular word in the generators of a group given by a grou ...

s, corresponding to finite group presentations, via combinatorial curvature conditions and derives algebraic and algorithmic properties of groups from such analysis. Bass–Serre theory, introduced in the 1977 book of Serre, derives structural algebraic information about groups by studying group actions on simplicial trees. External precursors of geometric group theory include the study of lattices in Lie groups, especially Mostow's rigidity theorem, the study of

Kleinian group In mathematics, a Kleinian group is a discrete subgroup of the group of orientation-preserving isometries of hyperbolic 3-space . The latter, identifiable with , is the quotient group of the 2 by 2 complex matrices of determinant 1 by their ...

s, and the progress achieved in

and hyperbolic geometry in the 1970s and early 1980s, spurred, in particular, by

William Thurston William Paul Thurston (October 30, 1946August 21, 2012) was an American mathematician. He was a pioneer in the field of low-dimensional topology and was awarded the Fields Medal in 1982 for his contributions to the study of 3-manifolds. Thursto ...

's Geometrization program. The emergence of geometric group theory as a distinct area of mathematics is usually traced to the late 1980s and early 1990s. It was spurred by the 1987 monograph of Mikhail Gromov ''"Hyperbolic groups"''Mikhail Gromov, ''Hyperbolic Groups'', in "Essays in Group Theory" (Steve M. Gersten, ed.), MSRI Publ. 8, 1987, pp. 75–263. that introduced the notion of a

hyperbolic group In group theory, more precisely in geometric group theory, a hyperbolic group, also known as a ''word hyperbolic group'' or ''Gromov hyperbolic group'', is a finitely generated group equipped with a word metric satisfying certain properties abstra ...

(also known as ''word-hyperbolic'' or ''Gromov-hyperbolic'' or ''negatively curved'' group), which captures the idea of a finitely generated group having large-scale negative curvature, and by his subsequent monograph ''Asymptotic Invariants of Infinite Groups'', that outlined Gromov's program of understanding discrete groups up to

quasi-isometry In mathematics, a quasi-isometry is a function between two metric spaces that respects large-scale geometry of these spaces and ignores their small-scale details. Two metric spaces are quasi-isometric if there exists a quasi-isometry between them. ...

. The work of Gromov had a transformative effect on the study of discrete groups and the phrase "geometric group theory" started appearing soon afterwards. (see e.g.).

Modern themes and developments

Notable themes and developments in geometric group theory in 1990s and 2000s include: *Gromov's program to study quasi-isometric properties of groups. :A particularly influential broad theme in the area is Gromov's program of classifying finitely generated groups according to their large scale geometry. Formally, this means classifying finitely generated groups with their

up to

. This program involves: :#The study of properties that are invariant under

. Examples of such properties of finitely generated groups include: the growth rate of a finitely generated group; the isoperimetric function or

Dehn function In the mathematical subject of geometric group theory, a Dehn function, named after Max Dehn, is an optimal function associated to a finite group presentation which bounds the ''area'' of a ''relation'' in that group (that is a freely reduced word ...

of a

finitely presented group In mathematics, a presentation is one method of specifying a group. A presentation of a group ''G'' comprises a set ''S'' of generators—so that every element of the group can be written as a product of powers of some of these generators—and ...

; the number of ends of a group; hyperbolicity of a group; the

homeomorphism In the mathematical field of topology, a homeomorphism, topological isomorphism, or bicontinuous function is a bijective and continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isom ...

type of the

Gromov boundary In mathematics, the Gromov boundary of a δ-hyperbolic space (especially a hyperbolic group) is an abstract concept generalizing the boundary sphere of hyperbolic space. Conceptually, the Gromov boundary is the set of all points at infinity. F ...

of a hyperbolic group;

asymptotic cone In mathematics, an ultralimit is a geometric construction that assigns to a sequence of metric spaces ''Xn'' a limiting metric space. The notion of an ultralimit captures the limiting behavior of finite configurations in the spaces ''Xn'' and use ...

s of finitely generated groups (see e.g.); amenability of a finitely generated group; being virtually

abelian Abelian may refer to: Mathematics Group theory * Abelian group, a group in which the binary operation is commutative ** Category of abelian groups (Ab), has abelian groups as objects and group homomorphisms as morphisms * Metabelian group, a grou ...

(that is, having an abelian subgroup of finite

index Index (or its plural form indices) may refer to: Arts, entertainment, and media Fictional entities * Index (''A Certain Magical Index''), a character in the light novel series ''A Certain Magical Index'' * The Index, an item on a Halo megastru ...

); being virtually

nilpotent In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n, called the index (or sometimes the degree), such that x^n=0. The term was introduced by Benjamin Peirce in the context of his work on the cl ...

; being virtually free; being finitely presentable; being a finitely presentable group with solvable Word Problem; and others. :#Theorems which use quasi-isometry invariants to prove algebraic results about groups, for example: Gromov's polynomial growth theorem; Stallings' ends theorem;

Mostow rigidity theorem Mostow may refer to: People * George Mostow (1923–2017), American mathematician ** Mostow rigidity theorem * Jonathan Mostow Jonathan Mostow (born November 28, 1961) is an American film director, screenwriter, and producer. He has directed f ...

. :#Quasi-isometric rigidity theorems, in which one classifies algebraically all groups that are quasi-isometric to some given group or metric space. This direction was initiated by the work of

Schwartz Schwartz may refer to: *Schwartz (surname), a surname (and list of people with the name) *Schwartz (brand), a spice brand *Schwartz's, a delicatessen in Montreal, Quebec, Canada *Schwartz Publishing, an Australian publishing house *"Danny Schwartz" ...

on quasi-isometric rigidity of rank-one lattices and the work of

Benson Farb Benson Stanley Farb (born October 25, 1967) is an American mathematician at the University of Chicago. His research fields include geometric group theory and low-dimensional topology. Early life A native of Norristown, Pennsylvania, Farb earned ...

and Lee Mosher on quasi-isometric rigidity of

Baumslag–Solitar group In the mathematical field of group theory, the Baumslag–Solitar groups are examples of two-generator one-relator groups that play an important role in combinatorial group theory and geometric group theory as (counter)examples and test-cases. ...

s. *The theory of word-hyperbolic and relatively hyperbolic groups. A particularly important development here is the work of Zlil Sela in 1990s resulting in the solution of the isomorphism problem for word-hyperbolic groups. The notion of a relatively hyperbolic groups was originally introduced by Gromov in 1987 and refined by Farb and

Brian Bowditch Brian Hayward Bowditch (born 1961
Bowditch's personal information page at the

, in the 1990s. The study of relatively hyperbolic groups gained prominence in the 2000s. *Interactions with mathematical logic and the study of the first-order theory of free groups. Particularly important progress occurred on the famous Tarski conjectures, due to the work of Sela as well as of Olga Kharlampovich and Alexei Myasnikov. The study of

limit group Limit or Limits may refer to: Arts and media * ''Limit'' (manga), a manga by Keiko Suenobu * ''Limit'' (film), a South Korean film * Limit (music), a way to characterize harmony * "Limit" (song), a 2016 single by Luna Sea * "Limits", a 2019 ...

s and introduction of the language and machinery of non-commutative algebraic geometry gained prominence. *Interactions with computer science, complexity theory and the theory of formal languages. This theme is exemplified by the development of the theory of automatic groups, a notion that imposes certain geometric and language theoretic conditions on the multiplication operation in a finitely generated group. *The study of isoperimetric inequalities, Dehn functions and their generalizations for finitely presented group. This includes, in particular, the work of Jean-Camille Birget, Aleksandr Olʹshanskiĭ,

Eliyahu Rips Eliyahu Rips ( he, אליהו ריפס; russian: Илья Рипс; lv, Iļja Ripss; born 12 December 1948) is an Israeli mathematician of Latvian origin known for his research in geometric group theory. He became known to the general public f ...

and Mark Sapir essentially characterizing the possible Dehn functions of finitely presented groups, as well as results providing explicit constructions of groups with fractional Dehn functions. *The theory of toral or JSJ-decompositions for

3-manifold In mathematics, a 3-manifold is a space that locally looks like Euclidean 3-dimensional space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane to a small enough observer, all 3-manifolds lo ...

s was originally brought into a group theoretic setting by Peter Kropholler. This notion has been developed by many authors for both finitely presented and finitely generated groups. *Connections with

geometric analysis Geometric analysis is a mathematical discipline where tools from differential equations, especially elliptic partial differential equations (PDEs), are used to establish new results in differential geometry and differential topology. The use of ...

, the study of C*-algebras associated with discrete groups and of the theory of free probability. This theme is represented, in particular, by considerable progress on the

Novikov conjecture The Novikov conjecture is one of the most important unsolved problems in topology. It is named for Sergei Novikov who originally posed the conjecture in 1965. The Novikov conjecture concerns the homotopy invariance of certain polynomials in the ...

and the

Baum–Connes conjecture In mathematics, specifically in operator K-theory, the Baum–Connes conjecture suggests a link between the K-theory of the reduced C*-algebra of a group and the K-homology of the classifying space of proper actions of that group. The conje ...

and the development and study of related group-theoretic notions such as topological amenability, asymptotic dimension, uniform embeddability into

Hilbert space In mathematics, Hilbert spaces (named after David Hilbert) allow generalizing the methods of linear algebra and calculus from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. Hilbert spaces arise natural ...

s, rapid decay property, and so on (see e.g.). *Interactions with the theory of quasiconformal analysis on metric spaces, particularly in relation to Cannon's conjecture about characterization of hyperbolic groups with

homeomorphic to the 2-sphere. * Finite subdivision rules, also in relation to Cannon's conjecture. *Interactions with

topological dynamics In mathematics, topological dynamics is a branch of the theory of dynamical systems in which qualitative, asymptotic properties of dynamical systems are studied from the viewpoint of general topology. Scope The central object of study in topolo ...

in the contexts of studying actions of discrete groups on various compact spaces and group compactifications, particularly convergence group methods *Development of the theory of group actions on

\mathbb R

-trees (particularly the

Rips machine In geometric group theory, the Rips machine is a method of studying the action of groups on R-trees. It was introduced in unpublished work of Eliyahu Rips in about 1991. An R-tree is a uniquely arcwise-connected metric space in which every arc ...

), and its applications. *The study of group actions on

CAT(0) space In mathematics, a \mathbf(k) space, where k is a real number, is a specific type of metric space. Intuitively, triangles in a \operatorname(k) space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature k. ...

s and CAT(0) cubical complexes, motivated by ideas from Alexandrov geometry. *Interactions with low-dimensional topology and hyperbolic geometry, particularly the study of 3-manifold groups (see, e.g.,),

mapping class group In mathematics, in the subfield of geometric topology, the mapping class group is an important algebraic invariant of a topological space. Briefly, the mapping class group is a certain discrete group corresponding to symmetries of the space. Mo ...

s of surfaces,

braid group A braid (also referred to as a plait) is a complex structure or pattern formed by interlacing two or more strands of flexible material such as textile yarns, wire, or hair. The simplest and most common version is a flat, solid, three-strande ...

s and

s. *Introduction of probabilistic methods to study algebraic properties of "random" group theoretic objects (groups, group elements, subgroups, etc.). A particularly important development here is the work of Gromov who used probabilistic methods to prove the existence of a finitely generated group that is not uniformly embeddable into a Hilbert space. Other notable developments include introduction and study of the notion of generic-case complexity for group-theoretic and other mathematical algorithms and algebraic rigidity results for generic groups. *The study of automata groups and iterated monodromy groups as groups of automorphisms of infinite rooted trees. In particular,

Grigorchuk's group In the mathematical area of group theory, the Grigorchuk group or the first Grigorchuk group is a finitely generated group constructed by Rostislav Grigorchuk that provided the first example of a finitely generated group of intermediate (that is ...

s of intermediate growth, and their generalizations, appear in this context. *The study of measure-theoretic properties of group actions on

measure space A measure space is a basic object of measure theory, a branch of mathematics that studies generalized notions of volumes. It contains an underlying set, the subsets of this set that are feasible for measuring (the -algebra) and the method that ...

s, particularly introduction and development of the notions of measure equivalence and orbit equivalence, as well as measure-theoretic generalizations of Mostow rigidity. *The study of unitary representations of discrete groups and Kazhdan's property (T) *The study of ''Out''(''F''_''n'') (the

outer automorphism group In mathematics, the outer automorphism group of a group, , is the quotient, , where is the automorphism group of and ) is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted . If is trivial and has a ...

of a

of rank ''n'') and of individual automorphisms of free groups. Introduction and the study of Culler-Vogtmann's

outer space Outer space, commonly shortened to space, is the expanse that exists beyond Earth and its atmosphere and between celestial bodies. Outer space is not completely empty—it is a near-perfect vacuum containing a low density of particles, pred ...

and of the theory of

train tracks A railway track (British English and UIC terminology) or railroad track (American English), also known as permanent way or simply track, is the structure on a railway or railroad consisting of the rails, fasteners, railroad ties (sleepers, ...

for free group automorphisms played a particularly prominent role here. *Development of

, particularly various accessibility results and the theory of tree lattices. Generalizations of Bass–Serre theory such as the theory of complexes of groups. *The study of

random walk In mathematics, a random walk is a random process that describes a path that consists of a succession of random steps on some mathematical space. An elementary example of a random walk is the random walk on the integer number line \mathbb Z ...

s on groups and related boundary theory, particularly the notion of Poisson boundary (see e.g.). The study of amenability and of groups whose amenability status is still unknown. *Interactions with finite group theory, particularly progress in the study of subgroup growth. *Studying subgroups and lattices in

linear group In mathematics, a matrix group is a group ''G'' consisting of invertible matrices over a specified field ''K'', with the operation of matrix multiplication. A linear group is a group that is isomorphic to a matrix group (that is, admitting a f ...

s, such as

SL(n, \mathbb R)

, and of other Lie groups, via geometric methods (e.g.

buildings A building, or edifice, is an enclosed structure with a roof and walls standing more or less permanently in one place, such as a house or factory (although there's also portable buildings). Buildings come in a variety of sizes, shapes, and func ...

), algebro-geometric tools (e.g.

algebraic group In mathematics, an algebraic group is an algebraic variety endowed with a group structure which is compatible with its structure as an algebraic variety. Thus the study of algebraic groups belongs both to algebraic geometry and group theory. Ma ...

s and representation varieties), analytic methods (e.g. unitary representations on Hilbert spaces) and arithmetic methods. *

Group cohomology In mathematics (more specifically, in homological algebra), group cohomology is a set of mathematical tools used to study groups using cohomology theory, a technique from algebraic topology. Analogous to group representations, group cohomology ...

, using algebraic and topological methods, particularly involving interaction with

and the use of morse-theoretic ideas in the combinatorial context; large-scale, or coarse (see e.g.) homological and cohomological methods. *Progress on traditional combinatorial group theory topics, such as the Burnside problem, the study of

Coxeter group In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean refle ...

s and Artin groups, and so on (the methods used to study these questions currently are often geometric and topological).

Examples

The following examples are often studied in geometric group theory: *

Amenable group In mathematics, an amenable group is a locally compact topological group ''G'' carrying a kind of averaging operation on bounded functions that is invariant under translation by group elements. The original definition, in terms of a finitely addit ...

s * Free Burnside groups * The infinite

cyclic group In group theory, a branch of abstract algebra in pure mathematics, a cyclic group or monogenous group is a group, denoted C''n'', that is generated by a single element. That is, it is a set of invertible elements with a single associative bina ...

Z *

Free group In mathematics, the free group ''F'S'' over a given set ''S'' consists of all words that can be built from members of ''S'', considering two words to be different unless their equality follows from the group axioms (e.g. ''st'' = ''suu''−1' ...

s *

Free product In mathematics, specifically group theory, the free product is an operation that takes two groups ''G'' and ''H'' and constructs a new The result contains both ''G'' and ''H'' as subgroups, is generated by the elements of these subgroups, and is ...

s *

Outer automorphism group In mathematics, the outer automorphism group of a group, , is the quotient, , where is the automorphism group of and ) is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted . If is trivial and has a ...

s Out(F_''n'') (via

) *

Hyperbolic group In group theory, more precisely in geometric group theory, a hyperbolic group, also known as a ''word hyperbolic group'' or ''Gromov hyperbolic group'', is a finitely generated group equipped with a word metric satisfying certain properties abstra ...

s *

Mapping class group In mathematics, in the subfield of geometric topology, the mapping class group is an important algebraic invariant of a topological space. Briefly, the mapping class group is a certain discrete group corresponding to symmetries of the space. Mo ...

s (automorphisms of surfaces) *

Symmetric group In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group ...

s *

Braid group A braid (also referred to as a plait) is a complex structure or pattern formed by interlacing two or more strands of flexible material such as textile yarns, wire, or hair. The simplest and most common version is a flat, solid, three-strande ...

s *

s * General Artin groups * Thompson's group ''F'' * CAT(0) groups *

Arithmetic group In mathematics, an arithmetic group is a group obtained as the integer points of an algebraic group, for example \mathrm_2(\Z). They arise naturally in the study of arithmetic properties of quadratic forms and other classical topics in number the ...

s * Automatic groups *

Fuchsian group In mathematics, a Fuchsian group is a discrete subgroup of PSL(2,R). The group PSL(2,R) can be regarded equivalently as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations o ...

s, and other groups acting properly discontinuously on symmetric spaces, in particular lattices in semisimple Lie groups. *

Wallpaper group A wallpaper is a mathematical object covering a whole Euclidean plane by repeating a motif indefinitely, in manner that certain isometries keep the drawing unchanged. To a given wallpaper there corresponds a group of such congruent transformati ...

s *

s * Fundamental groups of graphs of groups * Grigorchuk group

References

Books and monographs

These texts cover geometric group theory and related topics. * * * * * * * * * * * * * *{{cite book , first=John , last=Roe , title=Lectures on Coarse Geometry , url=https://books.google.com/books?id=jbsFCAAAQBAJ , year=2003 , series=University Lecture Series , volume=31 , publisher=American Mathematical Society , isbn=978-0-8218-3332-2

External links