Gekko (optimization software) on:
[Wikipedia]
[Google]
[Amazon]
The GEKKO Python package solves large-scale mixed-integer and differential algebraic equations with nonlinear programming solvers (
pip install gekko
GEKKO works on all platforms and with Python 2.7 and 3+. By default, the problem is sent to a public server where the solution is computed and returned to Python. There are Windows, MacOS, Linux, and ARM (Raspberry Pi) processor options to solve without an Internet connection. GEKKO is an extension of the APMonitor Optimization Suite but has integrated the modeling and solution visualization directly within Python. A mathematical model is expressed in terms of variables and equations such as the Hock & Schittkowski Benchmark Problem #71 used to test the performance of
from gekko import GEKKO
m = GEKKO() # Initialize gekko
# Initialize variables
x1 = m.Var(value=1, lb=1, ub=5)
x2 = m.Var(value=5, lb=1, ub=5)
x3 = m.Var(value=5, lb=1, ub=5)
x4 = m.Var(value=1, lb=1, ub=5)
# Equations
m.Equation(x1 * x2 * x3 * x4 >= 25)
m.Equation(x1 ** 2 + x2 ** 2 + x3 ** 2 + x4 ** 2 40)
m.Obj(x1 * x4 * (x1 + x2 + x3) + x3) # Objective
m.solve(disp=False) # Solve
print("x1: " + str(x1.value))
print("x2: " + str(x2.value))
print("x3: " + str(x3.value))
print("x4: " + str(x4.value))
print("Objective: " + str(m.options.objfcnval))
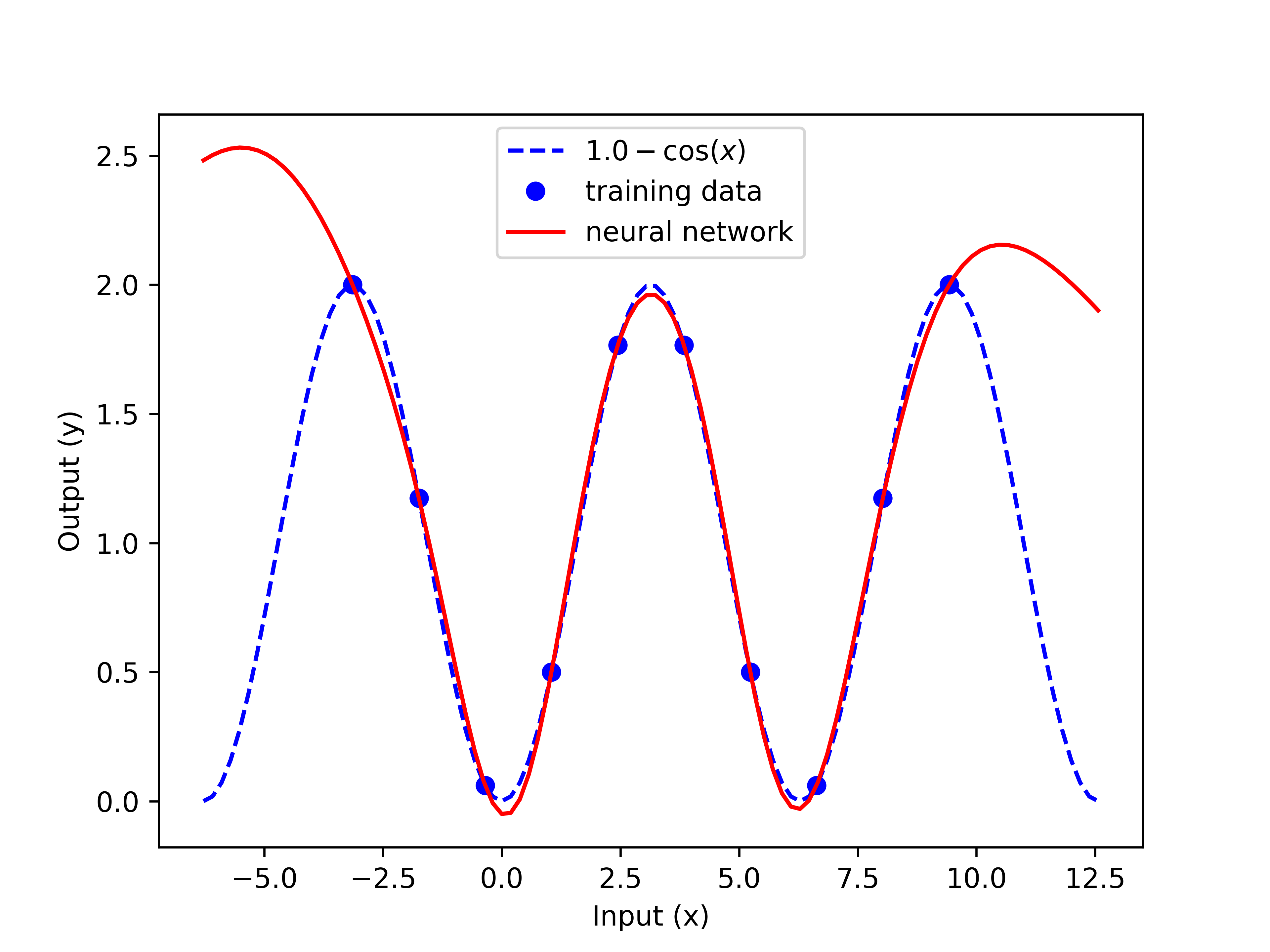 One application of
One application of
from gekko import brain
import numpy as np
b = brain.Brain()
b.input_layer(1)
b.layer(linear=3)
b.layer(tanh=3)
b.layer(linear=3)
b.output_layer(1)
x = np.linspace(-np.pi, 3 * np.pi, 20)
y = 1 - np.cos(x)
b.learn(x, y)
The neural network model is tested across the range of training data as well as for extrapolation to demonstrate poor predictions outside of the training data. Predictions outside the training data set are improved with hybrid machine learning that uses fundamental principles (if available) to impose a structure that is valid over a wider range of conditions. In the example above, the hyperbolic tangent activation function (hidden layer 2) could be replaced with a sine or cosine function to improve extrapolation. The final part of the script displays the neural network model, the original function, and the sampled data points used for fitting.
import matplotlib.pyplot as plt
xp = np.linspace(-2 * np.pi, 4 * np.pi, 100)
yp = b.think(xp)
plt.figure()
plt.plot(x, y, "bo")
plt.plot(xp, yp "r-")
plt.show()
 Optimal control is the use of
Optimal control is the use of
from gekko import GEKKO
import numpy as np
import matplotlib.pyplot as plt
m = GEKKO() # initialize gekko
nt = 101
m.time = np.linspace(0, 2, nt)
# Variables
x1 = m.Var(value=1)
x2 = m.Var(value=0)
u = m.Var(value=0, lb=-1, ub=1)
p = np.zeros(nt) # mark final time point
p 1= 1.0
final = m.Param(value=p)
# Equations
m.Equation(x1.dt() u)
m.Equation(x2.dt() 0.5 * x1 ** 2)
m.Obj(x2 * final) # Objective function
m.options.IMODE = 6 # optimal control mode
m.solve() # solve
plt.figure(1) # plot results
plt.plot(m.time, x1.value, "k-", label=r"$x_1$")
plt.plot(m.time, x2.value, "b-", label=r"$x_2$")
plt.plot(m.time, u.value, "r--", label=r"$u$")
plt.legend(loc="best")
plt.xlabel("Time")
plt.ylabel("Value")
plt.show()
GEKKO Overview with Machine Learning and Optimization
GEKKO Documentation
GEKKO Source Code
GEKKO on PyPI
for Python pip install * GEKKO is open-source product o
National Science Foundation (NSF) research grant 1547110
References to APMonitor and GEKKO
in the literature
18 examples of GEKKO
machine learning, optimal control, data regression {{DEFAULTSORT:Gekko Numerical programming languages Mathematical optimization software
IPOPT
IPOPT, short for "Interior Point OPTimizer, pronounced I-P-Opt", is a software library for large scale nonlinear optimization of continuous systems. It is written in Fortran and C and is released under the EPL (formerly CPL). IPOPT implement ...
, APOPT
APOPT (for Advanced Process OPTimizer) is a software package for solving large-scale optimization problems of any of these forms:
* Linear programming (LP)
* Quadratic programming (QP)
* Quadratically constrained quadratic program (QCQP)
* Nonli ...
, BPOPT, SNOPT, MINOS
In Greek mythology, Minos (; grc-gre, Μίνως, ) was a King of Crete, son of Zeus and Europa. Every nine years, he made King Aegeus pick seven young boys and seven young girls to be sent to Daedalus's creation, the labyrinth, to be eat ...
). Modes of operation include machine learning, data reconciliation, real-time optimization, dynamic simulation, and nonlinear model predictive control Model predictive control (MPC) is an advanced method of process control that is used to control a process while satisfying a set of constraints. It has been in use in the process industries in chemical plants and oil refineries since the 1980s. In r ...
. In addition, the package solves Linear programming
Linear programming (LP), also called linear optimization, is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements are represented by linear relationships. Linear programming is ...
(LP), Quadratic programming
Quadratic programming (QP) is the process of solving certain mathematical optimization problems involving quadratic functions. Specifically, one seeks to optimize (minimize or maximize) a multivariate quadratic function subject to linear constr ...
(QP), Quadratically constrained quadratic program In mathematical optimization, a quadratically constrained quadratic program (QCQP) is an optimization problem in which both the objective function and the constraints are quadratic functions. It has the form
: \begin
& \text && \tfrac12 x^\mathr ...
(QCQP), Nonlinear programming
In mathematics, nonlinear programming (NLP) is the process of solving an optimization problem where some of the constraints or the objective function are nonlinear. An optimization problem is one of calculation of the extrema (maxima, minima or st ...
(NLP), Mixed integer programming
Linear programming (LP), also called linear optimization, is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements are represented by linear relationships. Linear programming is ...
(MIP), and Mixed integer linear programming (MILP). GEKKO is available in Python and installed with pip from PyPI of the Python Software Foundation.
nonlinear programming
In mathematics, nonlinear programming (NLP) is the process of solving an optimization problem where some of the constraints or the objective function are nonlinear. An optimization problem is one of calculation of the extrema (maxima, minima or st ...
solvers. This particular optimization problem has an objective function and subject to the inequality constraint and equality constraint . The four variables must be between a lower bound of 1 and an upper bound of 5. The initial guess values are . This optimization problem is solved with GEKKO as shown below.
Applications of GEKKO
Applications include cogeneration (power and heat), drilling automation, severe slugging control, solar thermal energy production,solid oxide fuel cell
A solid oxide fuel cell (or SOFC) is an electrochemical conversion device that produces electricity directly from oxidizing a fuel. Fuel cells are characterized by their electrolyte material; the SOFC has a solid oxide or ceramic electrolyte.
A ...
s, flow assurance, Enhanced oil recovery
Enhanced oil recovery (abbreviated EOR), also called tertiary recovery, is the extraction of crude oil from an oil field that cannot be extracted otherwise. EOR can extract 30% to 60% or more of a reservoir's oil, compared to 20% to 40% using ...
, Essential oil extraction, and Unmanned Aerial Vehicles (UAVs). There are many other references to APMonitor and GEKKO as a sample of the types of applications that can be solved. GEKKO is developed from the National Science Foundation (NSF) research grant #1547110 and is detailed in a Special Issue collection on combined scheduling and control. Other notable mentions of GEKKO are the listing in the Decision Tree for Optimization Software, added support for APOPT
APOPT (for Advanced Process OPTimizer) is a software package for solving large-scale optimization problems of any of these forms:
* Linear programming (LP)
* Quadratic programming (QP)
* Quadratically constrained quadratic program (QCQP)
* Nonli ...
and BPOPT solvers, projects reports of the online Dynamic Optimization course from international participants. GEKKO is a topic in online forums where users are solving optimization and optimal control problems. GEKKO is used for advanced control in the Temperature Control Lab (TCLab) for process control education at 20 universities.
Machine Learning
 One application of
One application of machine learning
Machine learning (ML) is a field of inquiry devoted to understanding and building methods that 'learn', that is, methods that leverage data to improve performance on some set of tasks. It is seen as a part of artificial intelligence.
Machine ...
is to perform regression from training data to build a correlation. In this example, deep learning generates a model from training data that is generated with the function . An artificial neural network
Artificial neural networks (ANNs), usually simply called neural networks (NNs) or neural nets, are computing systems inspired by the biological neural networks that constitute animal brains.
An ANN is based on a collection of connected units ...
with three layers is used for this example. The first layer is linear, the second layer has a hyperbolic tangent activation function, and the third layer is linear. The program produces parameter weights that minimize the sum of squared errors between the measured data points and the neural network predictions at those points. GEKKO uses gradient-based optimizers to determine the optimal weight values instead of standard methods such as backpropagation
In machine learning, backpropagation (backprop, BP) is a widely used algorithm for training feedforward artificial neural networks. Generalizations of backpropagation exist for other artificial neural networks (ANNs), and for functions gener ...
. The gradients are determined by automatic differentiation, similar to other popular packages. The problem is solved as a constrained optimization problem and is converged when the solver satisfies Karush–Kuhn–Tucker conditions
In mathematical optimization, the Karush–Kuhn–Tucker (KKT) conditions, also known as the Kuhn–Tucker conditions, are first derivative tests (sometimes called first-order necessary conditions) for a solution in nonlinear programming to be ...
. Using a gradient-based optimizer allows additional constraints that may be imposed with domain knowledge of the data or system.
Optimal Control
 Optimal control is the use of
Optimal control is the use of mathematical optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfi ...
to obtain a policy that is constrained by differential , equality , or inequality equations and minimizes an objective/reward function . The basic optimal control is solved with GEKKO by integrating the objective and transcribing the differential equation into algebraic form with orthogonal collocation on finite elements.
See also
*APMonitor
Advanced process monitor (APMonitor) is a modeling language for differential algebraic ( DAE) equations. It is a free web-service or local server for solving representations of physical systems in the form of implicit DAE models. APMonitor is ...
and Python.
References
External links
GEKKO Overview with Machine Learning and Optimization
GEKKO Documentation
GEKKO Source Code
GEKKO on PyPI
for Python pip install * GEKKO is open-source product o
National Science Foundation (NSF) research grant 1547110
References to APMonitor and GEKKO
in the literature
18 examples of GEKKO
machine learning, optimal control, data regression {{DEFAULTSORT:Gekko Numerical programming languages Mathematical optimization software