Fibonacci sequence

In mathematics, the Fibonacci numbers, commonly denoted , form a sequence, the Fibonacci sequence, in which each number is the sum of the two preceding ones. The sequence commonly starts from 0 and 1, although some authors start the sequence from 1 and 1 or sometimes (as did Fibonacci) from 1 and 2.
Starting from 0 and 1, the first few values in the sequence are:
:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144.

The Fibonacci numbers were first described in Indian mathematics, as early as 200 BC in work by Pingala on enumerating possible patterns of Sanskrit poetry formed from syllables of two lengths. They are named after the Italian mathematician Leonardo of Pisa, later known as Fibonacci, who introduced the sequence to Western European mathematics in his 1202 book '' Liber Abaci''.

Fibonacci numbers appear unexpectedly often in mathematics, so much so that there is an entire journal dedicated to their study, the '' Fibonacci Quarterly''. Applications of Fibonacci numbers include computer algorithms such as the Fibonacci search technique and the Fibonacci heap data structure, and graphs called Fibonacci cubes used for interconnecting parallel and distributed systems. They also appear in biological settings, such as branching in trees, the arrangement of leaves on a stem, the fruit sprouts of a pineapple, the flowering of an artichoke, an uncurling fern, and the arrangement of a pine cone's bracts.

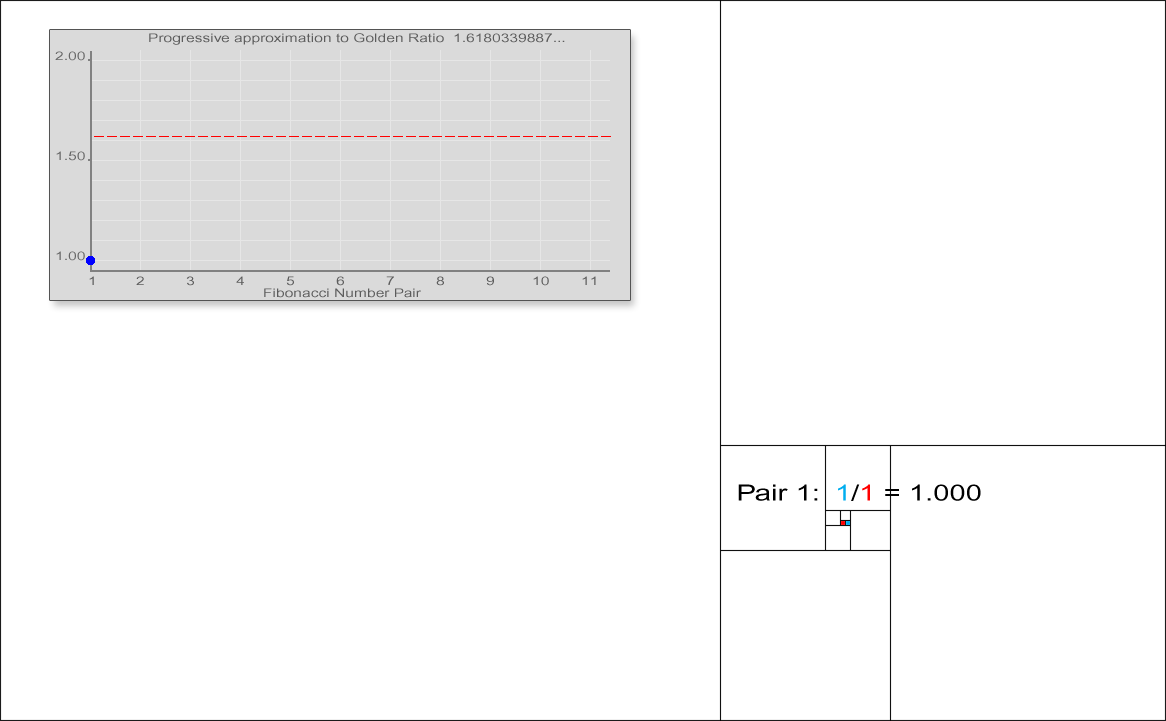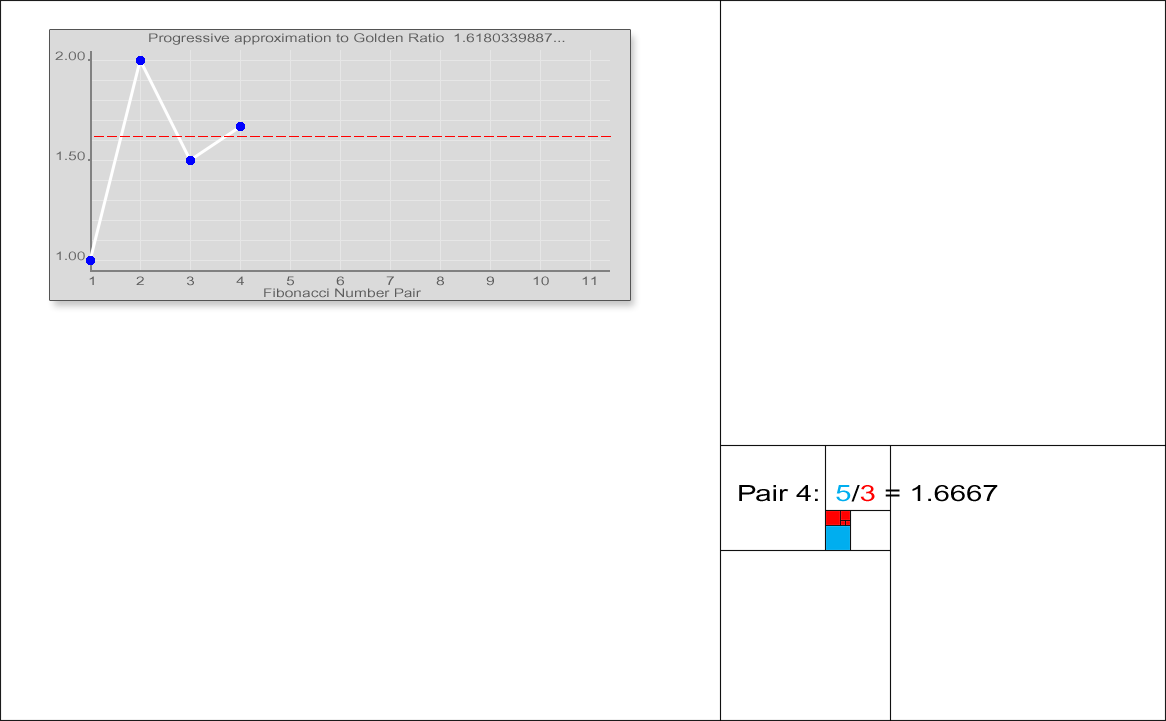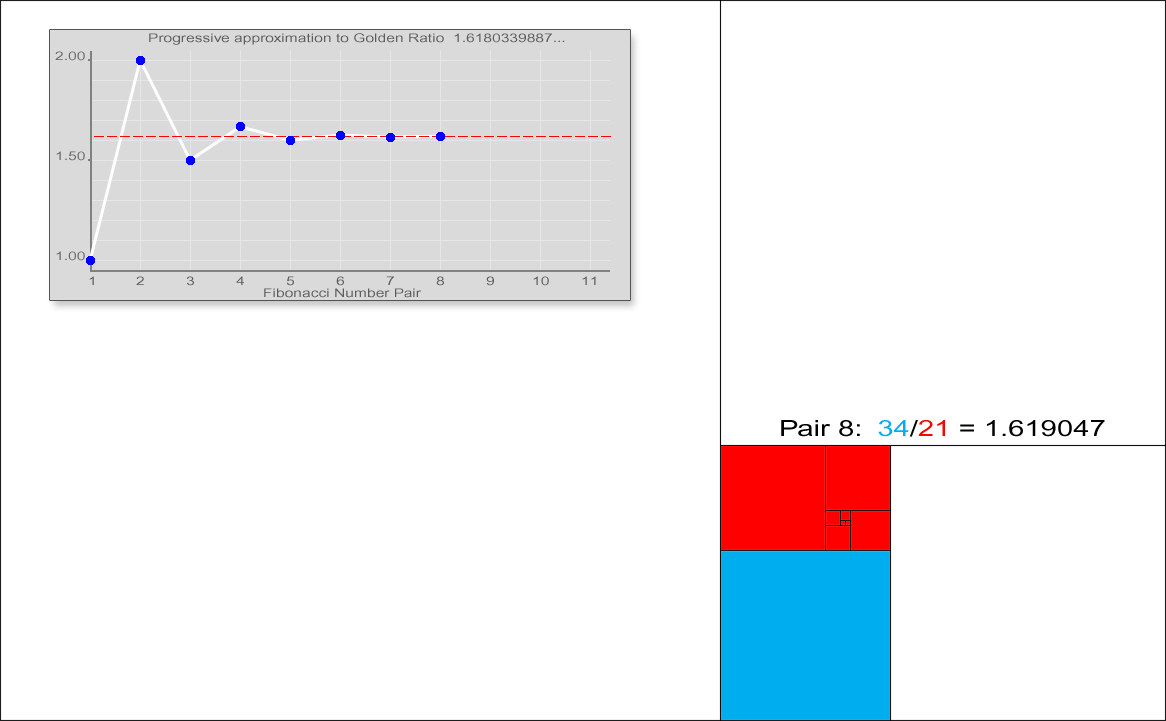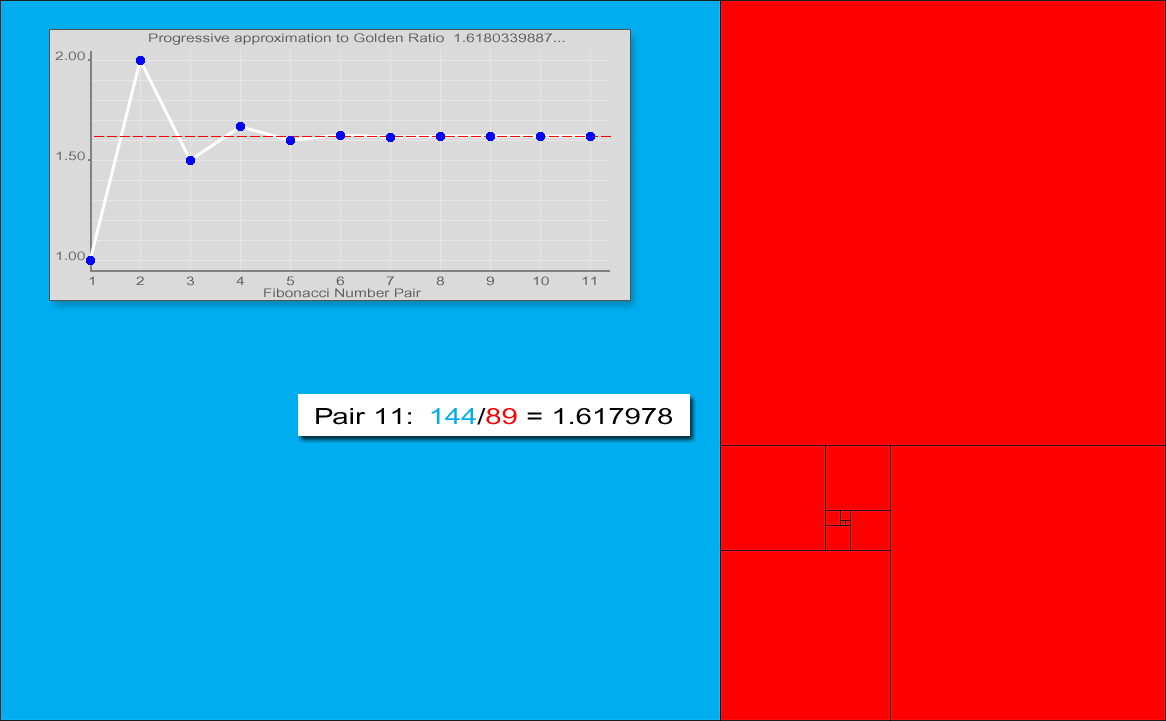
Fibonacci numbers are also strongly related to the golden ratio: Binet's formula expresses the th Fibonacci number in terms of and the golden ratio, and implies that the ratio of two consecutive Fibonacci numbers tends to the golden ratio as increases. Fibonacci numbers are also closely related to Lucas numbers, which obey the same recurrence relation and with the Fibonacci numbers form a complementary pair of Lucas sequences.

Definition

The Fibonacci numbers may be defined by the recurrence relation
$F_0=0,\quad F_1= 1,$
and
$F_n=F_ + F_$
for .

Under some older definitions, the value $F_0 = 0$ is omitted, so that the sequence starts with $F_1=F_2=1,$ and the recurrence $F_n=F_ + F_$ is valid for .

The first 20 Fibonacci numbers are:
:

History

The Fibonacci sequence appears in Indian mathematics, in connection with Sanskrit prosody. In the Sanskrit poetic tradition, there was interest in enumerating all patterns of long (L) syllables of 2 units duration, juxtaposed with short (S) syllables of 1 unit duration. Counting the different patterns of successive L and S with a given total duration results in the Fibonacci numbers: the number of patterns of duration units is .

Knowledge of the Fibonacci sequence was expressed as early as Pingala ( 450 BC–200 BC). Singh cites Pingala's cryptic formula ''misrau cha'' ("the two are mixed") and scholars who interpret it in context as saying that the number of patterns for beats () is obtained by adding one to the cases and one to the cases. Bharata Muni also expresses knowledge of the sequence in the '' Natya Shastra'' (c. 100 BC–c. 350 AD).
However, the clearest exposition of the sequence arises in the work of Virahanka (c. 700 AD), whose own work is lost, but is available in a quotation by Gopala (c. 1135):

Variations of two earlier meters s the variation.. For example, for meter of lengthfour, variations of meters of two ndthree being mixed, five happens. orks out examples 8, 13, 21.. In this way, the process should be followed in all ''mātrā-vṛttas'' rosodic combinations

Hemachandra (c. 1150) is credited with knowledge of the sequence as well, writing that "the sum of the last and the one before the last is the number ... of the next mātrā-vṛtta."

Outside India, the Fibonacci sequence first appears in the book '' Liber Abaci'' (''The Book of Calculation'', 1202) by Fibonacci where it is used to calculate the growth of rabbit populations. Fibonacci considers the growth of an idealized (biologically unrealistic) rabbit population, assuming that: a newly born breeding pair of rabbits are put in a field; each breeding pair mates at the age of one month, and at the end of their second month they always produce another pair of rabbits; and rabbits never die, but continue breeding forever. Fibonacci posed the puzzle: how many pairs will there be in one year?

* At the end of the first month, they mate, but there is still only 1 pair.
* At the end of the second month they produce a new pair, so there are 2 pairs in the field.
* At the end of the third month, the original pair produce a second pair, but the second pair only mate to gestate for a month, so there are 3 pairs in all.
* At the end of the fourth month, the original pair has produced yet another new pair, and the pair born two months ago also produces their first pair, making 5 pairs.

At the end of the th month, the number of pairs of rabbits is equal to the number of mature pairs (that is, the number of pairs in month ) plus the number of pairs alive last month (month ). The number in the th month is the th Fibonacci number.

The name "Fibonacci sequence" was first used by the 19th-century number theorist Édouard Lucas.

Relation to the golden ratio

Closed-form expression

Like every sequence defined by a linear recurrence with constant coefficients, the Fibonacci numbers have a closed-form expression. It has become known as Binet's formula, named after French mathematician Jacques Philippe Marie Binet, though it was already known by Abraham de Moivre and Daniel Bernoulli:

$F_n = \frac = \frac,$
where
$\varphi = \frac \approx 1.61803\,39887\ldots$
is the golden ratio, and is its conjugate:
$\psi = \frac = 1 - \varphi = - \approx -0.61803\,39887\ldots.$

Since $\psi = -\varphi^$, this formula can also be written as
$F_n = \frac = \frac.$

To see the relation between the sequence and these constants, note that and are both solutions of the equation
$x^2 = x + 1 \quad\text\quad x^n = x^ + x^,$
so the powers of and satisfy the Fibonacci recursion. In other words,
$\varphi^n = \varphi^ + \varphi^$
and
$\psi^n = \psi^ + \psi^.$

It follows that for any values and , the sequence defined by
$U_n=a \varphi^n + b \psi^n$
satisfies the same recurrence.
$U_n = a\varphi^n + b\psi^n = a(\varphi^ + \varphi^) + b(\psi^ + \psi^) = a\varphi^ + b\psi^ + a\varphi^ + b\psi^ = U_ + U_$

If and are chosen so that and then the resulting sequence must be the Fibonacci sequence. This is the same as requiring and satisfy the system of equations:
$\left\{\begin{array}{l} a + b = 0\\ \varphi a + \psi b = 1\end{array}\right.$
which has solution
$a = \frac{1}{\varphi-\psi} = \frac{1}{\sqrt 5},\quad b = -a,$
producing the required formula.

Taking the starting values and to be arbitrary constants, a more general solution is:
$U_n=a\varphi^n+b\psi^n$
where
$a=\frac{U_1-U_0\psi}{\sqrt 5}$
$b=\frac{U_0\varphi-U_1}{\sqrt 5}.$

Computation by rounding

Since
$\left, \frac{\psi^{n{\sqrt 5}\ < \frac{1}{2}$

for all , the number is the closest integer to $\frac{\varphi^n}{\sqrt 5}$. Therefore, it can be found by rounding, using the nearest integer function:
$F_n=\left\lfloor\frac{\varphi^n}{\sqrt 5}\right\rceil,\ n \geq 0.$

In fact, the rounding error is very small, being less than 0.1 for , and less than 0.01 for .

Fibonacci numbers can also be computed by truncation, in terms of the floor function:
$F_n=\left\lfloor\frac{\varphi^n}{\sqrt 5} + \frac{1}{2}\right\rfloor,\ n \geq 0.$

As the floor function is monotonic, the latter formula can be inverted for finding the index of the smallest Fibonacci number that is not less than a positive integer :
$n(F) = \left\lceil \log_\varphi \left(F\cdot\sqrt{5} - \frac{1}{2}\right) \right\rceil,$
where $\log_\varphi(x) = \ln(x)/\ln(\varphi) = \log_{10}(x)/\log_{10}(\varphi)$, $\ln(\varphi) = 0.481211\ldots$, and $\log_{10}(\varphi) = 0.208987\ldots$.

Magnitude

Since ''F_n'' is asymptotic to $\varphi^n/\sqrt5$, the number of digits in ''F''_''n'' is asymptotic to $n\log_{10}\varphi\approx 0.2090\, n$. As a consequence, for every integer ''d'' > 1 there are either 4 or 5 Fibonacci numbers with ''d'' decimal digits.

More generally, in the base ''b'' representation, the number of digits in ''F''_''n'' is asymptotic to $n\log_b\varphi.$

Limit of consecutive quotients

Johannes Kepler observed that the ratio of consecutive Fibonacci numbers converges. He wrote that "as 5 is to 8 so is 8 to 13, practically, and as 8 is to 13, so is 13 to 21 almost", and concluded that these ratios approach the golden ratio $\varphi\colon$
$\lim_{n\to\infty}\frac{F_{n+1{F_n}=\varphi.$

This convergence holds regardless of the starting values $U_0$ and $U_1$, unless $U_1 = -U_0/\varphi$. This can be verified using Binet's formula. For example, the initial values 3 and 2 generate the sequence 3, 2, 5, 7, 12, 19, 31, 50, 81, 131, 212, 343, 555, ... The ratio of consecutive terms in this sequence shows the same convergence towards the golden ratio.

In general, $\lim_{n\to\infty}\frac{F_{n+m{F_n}=\varphi^m$, because the ratios between consecutive Fibonacci numbers approaches $\varphi$.

:

Decomposition of powers

Since the golden ratio satisfies the equation
$\varphi^2 = \varphi + 1,$

this expression can be used to decompose higher powers $\varphi^n$ as a linear function of lower powers, which in turn can be decomposed all the way down to a linear combination of $\varphi$ and 1. The resulting recurrence relationships yield Fibonacci numbers as the linear coefficients:
$\varphi^n = F_n\varphi + F_{n-1}.$
This equation can be proved by induction on :
$\varphi^{n+1} = (F_n\varphi + F_{n-1})\varphi = F_n\varphi^2 + F_{n-1}\varphi = F_n(\varphi+1) + F_{n-1}\varphi = (F_n + F_{n-1})\varphi + F_n = F_{n+1}\varphi + F_n.$
For $\psi = -1/\varphi$, it is also the case that $\psi^2 = \psi + 1$ and it is also the case that
$\psi^n = F_n\psi + F_{n-1}.$

These expressions are also true for if the Fibonacci sequence ''F_n'' is extended to negative integers using the Fibonacci rule $F_n = F_{n+2} - F_{n+1}.$

Identification

Binet's formula provides a proof that a positive integer ''x'' is a Fibonacci number if and only if at least one of $5x^2+4$ or $5x^2-4$ is a perfect square. This is because Binet's formula, which can be written as $F_n = (\varphi^n - (-1)^n \varphi^{-n}) / \sqrt{5}$, can be multiplied by $\sqrt{5} \varphi^n$ and solved as a quadratic equation in $\varphi^n$ via the quadratic formula:

$\varphi^n = \frac{F_n\sqrt{5} \pm \sqrt{5{F_n}^2 + 4(-1)^n{2}.$

Comparing this to $\varphi^n = F_n \varphi + F_{n-1} = (F_n\sqrt{5} + F_n + 2 F_{n-1})/2$, it follows that
:$5{F_n}^2 + 4(-1)^n = (F_n + 2F_{n-1})^2\,.$
In particular, the left-hand side is a perfect square.

Matrix form

A 2-dimensional system of linear difference equations that describes the Fibonacci sequence is

${F_{k+2} \choose F_{k+1 = \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix} {F_{k+1} \choose F_{k$
alternatively denoted
$\vec F_{k+1} = \mathbf{A} \vec F_{k},$

which yields $\vec F_{n} = \mathbf{A}^n \vec F_{0}$. The eigenvalues of the matrix are $\varphi=\frac12(1+\sqrt5)$ and $\psi=-\varphi^{-1}=\frac12(1-\sqrt5)$ corresponding to the respective eigenvectors
$\vec \mu={\varphi \choose 1}$
and
$\vec\nu={-\varphi^{-1} \choose 1}.$
As the initial value is
$\vec F_0={1 \choose 0}=\frac{1}{\sqrt{5\vec{\mu}-\frac{1}{\sqrt{5\vec{\nu},$
it follows that the th term is
$\begin{align}\vec F_{n} &= \frac{1}{\sqrt{5A^n\vec\mu-\frac{1}{\sqrt{5A^n\vec\nu \\ &= \frac{1}{\sqrt{5\varphi^n\vec\mu-\frac{1}{\sqrt{5(-\varphi)^{-n}\vec\nu~\\ & =\cfrac{1}{\sqrt{5\left(\cfrac{1+\sqrt{5{2}\right)^n{\varphi \choose 1}-\cfrac{1}{\sqrt{5\left(\cfrac{1-\sqrt{5{2}\right)^n{-\varphi^{-1}\choose 1}, \end{align}$
From this, the th element in the Fibonacci series
may be read off directly as a closed-form expression:
$F_{n} = \cfrac{1}{\sqrt{5\left(\cfrac{1+\sqrt{5{2}\right)^n-\cfrac{1}{\sqrt{5\left(\cfrac{1-\sqrt{5{2}\right)^n.$

Equivalently, the same computation may performed by diagonalization of through use of its eigendecomposition:
$\begin{align} A & = S\Lambda S^{-1} ,\\ A^n & = S\Lambda^n S^{-1}, \end{align}$
where $\Lambda=\begin{pmatrix} \varphi & 0 \\ 0 & -\varphi^{-1} \end{pmatrix}$ and $S=\begin{pmatrix} \varphi & -\varphi^{-1} \\ 1 & 1 \end{pmatrix}.$
The closed-form expression for the th element in the Fibonacci series is therefore given by

$\begin{align} {F_{n+1} \choose F_{n & = A^{n} {F_1 \choose F_0} \\ & = S \Lambda^n S^{-1} {F_1 \choose F_0} \\ & = S \begin{pmatrix} \varphi^n & 0 \\ 0 & (-\varphi)^{-n} \end{pmatrix} S^{-1} {F_1 \choose F_0} \\ & = \begin{pmatrix} \varphi & -\varphi^{-1} \\ 1 & 1 \end{pmatrix} \begin{pmatrix} \varphi^n & 0 \\ 0 & (-\varphi)^{-n} \end{pmatrix} \frac{1}{\sqrt{5\begin{pmatrix} 1 & \varphi^{-1} \\ -1 & \varphi \end{pmatrix} {1 \choose 0}, \end{align}$

which again yields
$F_{n} = \cfrac{\varphi^n-(-\varphi)^{-n{\sqrt{5.$

The matrix has a determinant of −1, and thus it is a 2×2 unimodular matrix.

This property can be understood in terms of the continued fraction representation for the golden ratio:

$\varphi = 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \ddots}.$

The Fibonacci numbers occur as the ratio of successive convergents of the continued fraction for , and the matrix formed from successive convergents of any continued fraction has a determinant of +1 or −1. The matrix representation gives the following closed-form expression for the Fibonacci numbers:

$\begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix}^n = \begin{pmatrix} F_{n+1} & F_n \\ F_n & F_{n-1} \end{pmatrix}.$

For a given , this matrix can be computed in arithmetic operations, using the exponentiation by squaring method.

Taking the determinant of both sides of this equation yields Cassini's identity,
$(-1)^n = F_{n+1}F_{n-1} - {F_n}^2.$

Moreover, since for any square matrix , the following identities can be derived (they are obtained from two different coefficients of the matrix product, and one may easily deduce the second one from the first one by changing into ),
$\begin{align} {F_m}{F_n} + {F_{m-1{F_{n-1 &= F_{m+n-1},\\ F_{m} F_{n+1} + F_{m-1} F_n &= F_{m+n} . \end{align}$

In particular, with ,
$\begin{array}{ll} F_{2 n-1} &= {F_n}^2 + {F_{n-1^2\\ F_{2 n} &= (F_{n-1}+F_{n+1})F_n\\ &= (2 F_{n-1}+F_n)F_n\\ &= (2 F_{n+1}-F_n)F_n. \end{array}$

These last two identities provide a way to compute Fibonacci numbers recursively in arithmetic operations and in time , where is the time for the multiplication of two numbers of digits. This matches the time for computing the th Fibonacci number from the closed-form matrix formula, but with fewer redundant steps if one avoids recomputing an already computed Fibonacci number (recursion with memoization).

Combinatorial identities

Combinatorial proofs

Most identities involving Fibonacci numbers can be proved using combinatorial arguments using the fact that $F_n$ can be interpreted as the number of ossibly emptysequences of 1s and 2s whose sum is $n-1$. This can be taken as the definition of $F_{n}$ with the conventions $F_{0}=0$, meaning no such sequence exists whose sum is −1, and $F_{1}=1$, meaning the empty sequence "adds up" to 0. In the following, $, {...},$ is the cardinality of a set:

: $F_{0} = 0 = , \{\},$
: $F_{1} = 1 = , \{\{\}\},$
: $F_{2} = 1 = , \{\{1\}\},$
: $F_{3} = 2 = , \{\{1,1\},\{2\}\},$
: $F_{4} = 3 = , \{\{1,1,1\},\{1,2\},\{2,1\}\},$
: $F_{5} = 5 = , \{\{1,1,1,1\},\{1,1,2\},\{1,2,1\},\{2,1,1\},\{2,2\}\},$

In this manner the recurrence relation
$F_{n} = F_{n-1} + F_{n-2}$
may be understood by dividing the $F_{n}$ sequences into two non-overlapping sets where all sequences either begin with 1 or 2:
$F_{n} = , \{\{1,...\},\{1,...\},...\}, + , \{\{2,...\},\{2,...\},...\},$
Excluding the first element, the remaining terms in each sequence sum to $n-2$ or $n-3$ and the cardinality of each set is $F_{n-1}$ or $F_{n-2}$ giving a total of $F_{n-1}+F_{n-2}$ sequences, showing this is equal to $F_{n}$.

In a similar manner it may be shown that the sum of the first Fibonacci numbers up to the ''n''th is equal to the (''n'' + 2)-nd Fibonacci number minus 1. In symbols:
$\sum_{i=1}^n F_i = F_{n+2} - 1$

This may be seen by dividing all sequences summing to $n+1$ based on the location of the first 2. Specifically, each set consists of those sequences that start $\{2,...\}, \{1,2,...\}, ...,$ until the last two sets $\{\{1,1,...,1,2\}\}, \{\{1,1,...,1\}\}$ each with cardinality 1.

Following the same logic as before, by summing the cardinality of each set we see that
: $F_{n+2} = F_{n} + F_{n-1} + ... + , \{\{1,1,...,1,2\}\}, + , \{\{1,1,...,1\}\},$
... where the last two terms have the value $F_{1} = 1$. From this it follows that $\sum_{i=1}^n F_i = F_{n+2}-1$.

A similar argument, grouping the sums by the position of the first 1 rather than the first 2 gives two more identities:
$\sum_{i=0}^{n-1} F_{2 i+1} = F_{2 n}$
and
$\sum_{i=1}^{n} F_{2 i} = F_{2 n+1}-1.$
In words, the sum of the first Fibonacci numbers with odd index up to $F_{2 n-1}$ is the (2''n'')th Fibonacci number, and the sum of the first Fibonacci numbers with even index up to $F_{2 n}$ is the (2''n'' + 1)th Fibonacci number minus 1.

A different trick may be used to prove
$\sum_{i=1}^n {F_i}^2 = F_{n} F_{n+1}$
or in words, the sum of the squares of the first Fibonacci numbers up to $F_{n}$ is the product of the ''n''th and (''n'' + 1)th Fibonacci numbers. To see this, begin with a Fibonacci rectangle of size $F_{n} \times F_{n+1}$ and decompose it into squares of size $F_{n}, F_{n-1}, ..., F_{1}$; from this the identity follows by comparing areas:

Symbolic method

The sequence $(F_n)_{n\in\mathbb N}$ is also considered using the symbolic method. More precisely, this sequence corresponds to a specifiable combinatorial class. The specification of this sequence is $\operatorname{Seq}(\mathcal{Z+Z^2})$. Indeed, as stated above, the $n$-th Fibonacci number equals the number of combinatorial compositions (ordered partitions) of $n-1$ using terms 1 and 2.

It follows that the ordinary generating function of the Fibonacci sequence, i.e. $\sum_{i=0}^\infty F_iz^i$, is the complex function $\frac{z}{1-z-z^2}$.

Induction proofs

Fibonacci identities often can be easily proved using mathematical induction.

For example, reconsider
$\sum_{i=1}^n F_i = F_{n+2} - 1.$
Adding $F_{n+1}$ to both sides gives
:$\sum_{i=1}^n F_i + F_{n+1} = F_{n+1} + F_{n+2} - 1$
and so we have the formula for $n+1$
$\sum_{i=1}^{n+1} F_i = F_{n+3} - 1$

Similarly, add ${F_{n+1^2$ to both sides of
$\sum_{i=1}^n {F_i}^2 = F_{n} F_{n+1}$
to give
$\sum_{i=1}^n {F_i}^2 + {F_{n+1^2 = F_{n+1}\left(F_{n} + F_{n+1}\right)$
$\sum_{i=1}^{n+1} {F_i}^2 = F_{n+1}F_{n+2}$

Binet formula proofs

The Binet formula is
$\sqrt5F_n = \varphi^n - \psi^n.$
This can be used to prove Fibonacci identities.

For example, to prove that $\sum_{i=1}^n F_i = F_{n+2} - 1$
note that the left hand side multiplied by $\sqrt5$ becomes
$\begin{align} 1 +& \varphi + \varphi^2 + \dots + \varphi^n - \left(1 + \psi + \psi^2 + \dots + \psi^n \right)\\ &= \frac{\varphi^{n+1}-1}{\varphi-1} - \frac{\psi^{n+1}-1}{\psi-1}\\ &= \frac{\varphi^{n+1}-1}{-\psi} - \frac{\psi^{n+1}-1}{-\varphi}\\ &= \frac{-\varphi^{n+2}+\varphi + \psi^{n+2}-\psi}{\varphi\psi}\\ &= \varphi^{n+2}-\psi^{n+2}-(\varphi-\psi)\\ &= \sqrt5(F_{n+2}-1)\\ \end{align}$
as required, using the facts $\varphi\psi =- 1$ and $\varphi-\psi=\sqrt5$ to simplify the equations.

Other identities

Numerous other identities can be derived using various methods. Here are some of them:

Cassini's and Catalan's identities

Cassini's identity states that
${F_n}^2 - F_{n+1}F_{n-1} = (-1)^{n-1}$
Catalan's identity is a generalization:
${F_n}^2 - F_{n+r}F_{n-r} = (-1)^{n-r}{F_r}^2$

d'Ocagne's identity

$F_m F_{n+1} - F_{m+1} F_n = (-1)^n F_{m-n}$
$F_{2 n} = {F_{n+1^2 - {F_{n-1^2 = F_n \left (F_{n+1}+F_{n-1} \right ) = F_nL_n$
where ''L''_''n'' is the ''nth Lucas number. The last is an identity for doubling ''n''; other identities of this type are
$F_{3 n} = 2{F_n}^3 + 3 F_n F_{n+1} F_{n-1} = 5{F_n}^3 + 3 (-1)^n F_n$
by Cassini's identity.

$F_{3 n+1} = {F_{n+1^3 + 3 F_{n+1}{F_n}^2 - {F_n}^3$
$F_{3 n+2} = {F_{n+1^3 + 3 {F_{n+1^2 F_n + {F_n}^3$
$F_{4 n} = 4 F_n F_{n+1} \left ({F_{n+1^2 + 2{F_n}^2 \right ) - 3{F_n}^2 \left ({F_n}^2 + 2{F_{n+1^2 \right )$
These can be found experimentally using lattice reduction, and are useful in setting up the special number field sieve to factorize a Fibonacci number.

More generally,

$F_{k n+c} = \sum_{i=0}^k {k\choose i} F_{c-i} {F_n}^i {F_{n+1^{k-i}.$

or alternatively

$F_{k n+c} = \sum_{i=0}^k {k\choose i} F_{c+i} {F_n}^i {F_{n-1^{k-i}.$

Putting in this formula, one gets again the formulas of the end of above section Matrix form.

Generating function

The generating function of the Fibonacci sequence is the power series
$s(x)=\sum_{k=0}^{\infty} F_k x^k = \sum_{k=1}^{\infty} F_k x^k = 0+x+x^2+2 x^3+3 x^4+\dots.$

This series is convergent for $, x, < \frac{1}{\varphi},$ and its sum has a simple closed-form:
$s(x)=\frac{x}{1-x-x^2}$

This can be proved by using the Fibonacci recurrence to expand each coefficient in the infinite sum:
$\begin{align} s(x) &= \sum_{k=0}^{\infty} F_k x^k \\ &= F_0 + F_1x + \sum_{k=2}^{\infty} F_k x^k \\ &= 0 + 1x + \sum_{k=2}^{\infty} F_k x^k \\ &= x + \sum_{k=2}^{\infty} \left( F_{k-1} + F_{k-2} \right) x^k \\ &= x + \sum_{k=2}^{\infty} F_{k-1} x^k + \sum_{k=2}^{\infty} F_{k-2} x^k \\ &= x + x\sum_{k=2}^{\infty} F_{k-1} x^{k-1} + x^2\sum_{k=2}^{\infty} F_{k-2} x^{k-2} \\ &= x + x\sum_{k=1}^{\infty} F_k x^k + x^2\sum_{k=0}^{\infty} F_k x^k \\ &= x + x s(x) + x^2 s(x). \end{align}$

Solving the equation
$s(x)=x+xs(x)+x^2 s(x)$
for ''s''(''x'') results in the closed form.

The partial fraction decomposition is given by
$s(x) = \frac{1}{\sqrt5}\left(\frac{1}{1 - \varphi x} - \frac{1}{1 - \psi x}\right)$
where $\varphi = \frac{1 + \sqrt{5{2}$ is the golden ratio and $\psi = \frac{1 - \sqrt{5{2}$ is its conjugate.

$-s\left(-\frac{1}{x}\right)$ gives the generating function for the negafibonacci numbers, and $s(x)$ satisfies the functional equation
$s(x)=s\left(-\frac{1}{x}\right).$

Reciprocal sums

Infinite sums over reciprocal Fibonacci numbers can sometimes be evaluated in terms of theta functions. For example, the sum of every odd-indexed reciprocal Fibonacci number can be written as
$\sum_{k=1}^\infty \frac{1}{F_{2 k-1 = \frac{\sqrt{5{4} \;\, \vartheta_2\!\left(0, \frac{3-\sqrt 5}{2}\right)^2 ,$

and the sum of squared reciprocal Fibonacci numbers as
$\sum_{k=1}^\infty \frac{1} = \frac{\sqrt{5{2},$

and there is a ''nested'' sum of squared Fibonacci numbers giving the reciprocal of the golden ratio,
$\sum_{k=1}^\infty \frac{(-1)^{k+1{\sum_{j=1}^k {F_{j^2} = \frac{\sqrt{5}-1}{2} .$

The sum of all even-indexed reciprocal Fibonacci numbers is
$\sum_{k=1}^{\infty} \frac{1}{F_{2 k = \sqrt{5} \left(L\bigl(\psi^2\bigr) - L\bigl(\psi^4\bigr)\right)$
with the Lambert series   $\textstyle L(q) := \sum_{k=1}^{\infty} \frac{q^k}{1-q^k} ,$   since   $\textstyle \frac{1}{F_{2 k = \sqrt{5} \left(\frac{\psi^{2 k{1-\psi^{2 k - \frac{\psi^{4 k{1-\psi^{4 k \right).$

So the reciprocal Fibonacci constant is
$\sum_{k=1}^{\infty} \frac{1}{F_k} = \sum_{k=1}^\infty \frac{1}{F_{2 k-1 + \sum_{k=1}^{\infty} \frac {1}{F_{2 k = 3.359885666243 \dots$

Moreover, this number has been proved irrational by Richard André-Jeannin.

Millin's series gives the identity
$\sum_{k=0}^{\infty} \frac{1}{F_{2^k = \frac{7 - \sqrt{5{2},$
which follows from the closed form for its partial sums as ''N'' tends to infinity:
$\sum_{k=0}^N \frac{1}{F_{2^k = 3 - \frac{F_{2^N-1{F_{2^N.$

Primes and divisibility

Divisibility properties

Every third number of the sequence is even (a multiple of $F_3=2$) and, more generally, every ''k''th number of the sequence is a multiple of ''F_k''. Thus the Fibonacci sequence is an example of a divisibility sequence. In fact, the Fibonacci sequence satisfies the stronger divisibility property
$\gcd(F_a,F_b,F_c,\ldots) = F_{\gcd(a,b,c,\ldots)}\,$
where is the greatest common divisor function.

In particular, any three consecutive Fibonacci numbers are pairwise coprime because both $F_1=1$ and $F_2 = 1$. That is,
:$\gcd(F_n, F_{n+1}) = \gcd(F_n, F_{n+2}) = \gcd(F_{n+1}, F_{n+2}) = 1$
for every ''n''.

Every prime number ''p'' divides a Fibonacci number that can be determined by the value of ''p'' modulo 5. If ''p'' is congruent to 1 or 4 (mod 5), then ''p'' divides ''F''_{''p'' − 1}, and if ''p'' is congruent to 2 or 3 (mod 5), then, ''p'' divides ''F''_''p'' + 1. The remaining case is that ''p'' = 5, and in this case ''p'' divides ''F''_p.

$\begin{cases} p =5 & \Rightarrow p \mid F_{p}, \\ p \equiv \pm1 \pmod 5 & \Rightarrow p \mid F_{p-1}, \\ p \equiv \pm2 \pmod 5 & \Rightarrow p \mid F_{p+1}.\end{cases}$

These cases can be combined into a single, non-piecewise formula, using the Legendre symbol:
$p \mid F_{p-\left(\frac{5}{p}\right)}.$

Primality testing

The above formula can be used as a primality test in the sense that if
$n \mid F_{n-\left(\frac{5}{n}\right)},$
where the Legendre symbol has been replaced by the Jacobi symbol, then this is evidence that ''n'' is a prime, and if it fails to hold, then ''n'' is definitely not a prime. If ''n'' is composite and satisfies the formula, then ''n'' is a ''Fibonacci pseudoprime''. When ''m'' is largesay a 500-bit numberthen we can calculate ''F''_''m'' (mod ''n'') efficiently using the matrix form. Thus

$\begin{pmatrix} F_{m+1} & F_m \\ F_m & F_{m-1} \end{pmatrix} \equiv \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix}^m \pmod n.$
Here the matrix power ''A''^''m'' is calculated using modular exponentiation, which can be adapted to matrices.

Fibonacci primes

A ''Fibonacci prime'' is a Fibonacci number that is prime. The first few are:

: 2, 3, 5, 13, 89, 233, 1597, 28657, 514229, ...

Fibonacci primes with thousands of digits have been found, but it is not known whether there are infinitely many.

''F''_''kn'' is divisible by ''F''_''n'', so, apart from ''F''₄ = 3, any Fibonacci prime must have a prime index. As there are arbitrarily long runs of composite numbers, there are therefore also arbitrarily long runs of composite Fibonacci numbers.

No Fibonacci number greater than ''F''₆ = 8 is one greater or one less than a prime number.

The only nontrivial square Fibonacci number is 144. Attila Pethő proved in 2001 that there is only a finite number of perfect power Fibonacci numbers. In 2006, Y. Bugeaud, M. Mignotte, and S. Siksek proved that 8 and 144 are the only such non-trivial perfect powers.

1, 3, 21, and 55 are the only triangular Fibonacci numbers, which was conjectured by Vern Hoggatt and proved by Luo Ming.

No Fibonacci number can be a perfect number. More generally, no Fibonacci number other than 1 can be multiply perfect, and no ratio of two Fibonacci numbers can be perfect.

Prime divisors

With the exceptions of 1, 8 and 144 (''F''₁ = ''F''₂, ''F''₆ and ''F''₁₂) every Fibonacci number has a prime factor that is not a factor of any smaller Fibonacci number (Carmichael's theorem). As a result, 8 and 144 (''F''₆ and ''F''₁₂) are the only Fibonacci numbers that are the product of other Fibonacci numbers.

The divisibility of Fibonacci numbers by a prime ''p'' is related to the Legendre symbol $\left(\tfrac{p}{5}\right)$ which is evaluated as follows:
$\left(\frac{p}{5}\right) = \begin{cases} 0 & \text{if } p = 5\\ 1 & \text{if } p \equiv \pm 1 \pmod 5\\ -1 & \text{if } p \equiv \pm 2 \pmod 5.\end{cases}$

If ''p'' is a prime number then
$F_p \equiv \left(\frac{p}{5}\right) \pmod p \quad \text{and}\quad F_{p-\left(\frac{p}{5}\right)} \equiv 0 \pmod p.$

For example,
$\begin{align} (\tfrac{2}{5}) &= -1, &F_3 &= 2, &F_2&=1, \\ (\tfrac{3}{5}) &= -1, &F_4 &= 3,&F_3&=2, \\ (\tfrac{5}{5}) &= 0, &F_5 &= 5, \\ (\tfrac{7}{5}) &= -1, &F_8 &= 21,&F_7&=13, \\ (\tfrac{11}{5})& = +1, &F_{10}& = 55, &F_{11}&=89. \end{align}$

It is not known whether there exists a prime ''p'' such that

$F_{p-\left(\frac{p}{5}\right)} \equiv 0 \pmod{p^2}.$

Such primes (if there are any) would be called Wall–Sun–Sun primes.

Also, if ''p'' ≠ 5 is an odd prime number then:
$5 {F_{\frac{p \pm 1}{2}^2 \equiv \begin{cases} \tfrac{1}{2} \left (5\left(\frac{p}{5}\right)\pm 5 \right ) \pmod p & \text{if } p \equiv 1 \pmod 4\\ \tfrac{1}{2} \left (5\left(\frac{p}{5}\right)\mp 3 \right ) \pmod p & \text{if } p \equiv 3 \pmod 4. \end{cases}$

Example 1. ''p'' = 7, in this case ''p'' ≡ 3 (mod 4) and we have:
$(\tfrac{7}{5}) = -1: \qquad \tfrac{1}{2}\left (5(\tfrac{7}{5})+3 \right ) =-1, \quad \tfrac{1}{2} \left (5(\tfrac{7}{5})-3 \right )=-4.$
$F_3=2 \text{ and } F_4=3.$
$5{F_3}^2=20\equiv -1 \pmod {7}\;\;\text{ and }\;\;5{F_4}^2=45\equiv -4 \pmod {7}$

Example 2. ''p'' = 11, in this case ''p'' ≡ 3 (mod 4) and we have:
$(\tfrac{11}{5}) = +1: \qquad \tfrac{1}{2}\left (5(\tfrac{11}{5})+3 \right )=4, \quad \tfrac{1}{2} \left (5(\tfrac{11}{5})- 3 \right )=1.$
$F_5=5 \text{ and } F_6=8.$
$5{F_5}^2=125\equiv 4 \pmod {11} \;\;\text{ and }\;\;5{F_6}^2=320\equiv 1 \pmod {11}$

Example 3. ''p'' = 13, in this case ''p'' ≡ 1 (mod 4) and we have:
$(\tfrac{13}{5}) = -1: \qquad \tfrac{1}{2}\left (5(\tfrac{13}{5})-5 \right ) =-5, \quad \tfrac{1}{2}\left (5(\tfrac{13}{5})+ 5 \right )=0.$
$F_6=8 \text{ and } F_7=13.$
$5{F_6}^2=320\equiv -5 \pmod {13} \;\;\text{ and }\;\;5{F_7}^2=845\equiv 0 \pmod {13}$

Example 4. ''p'' = 29, in this case ''p'' ≡ 1 (mod 4) and we have:
$(\tfrac{29}{5}) = +1: \qquad \tfrac{1}{2}\left (5(\tfrac{29}{5})-5 \right )=0, \quad \tfrac{1}{2}\left (5(\tfrac{29}{5})+5 \right )=5.$
$F_{14}=377 \text{ and } F_{15}=610.$
$5{F_{14^2=710645\equiv 0 \pmod {29} \;\;\text{ and }\;\;5{F_{15^2=1860500\equiv 5 \pmod {29}$

For odd ''n'', all odd prime divisors of ''F''_''n'' are congruent to 1 modulo 4, implying that all odd divisors of ''F''_''n'' (as the products of odd prime divisors) are congruent to 1 modulo 4.

For example,
$F_1 = 1, F_3 = 2, F_5 = 5, F_7 = 13, F_9 = 34 = 2 \cdot 17, F_{11} = 89, F_{13} = 233, F_{15} = 610 = 2 \cdot 5 \cdot 61.$

All known factors of Fibonacci numbers ''F''(''i'') for all ''i'' < 50000 are collected at the relevant repositories.

Periodicity modulo ''n''

If the members of the Fibonacci sequence are taken mod ''n'', the resulting sequence is periodic with period at most ''6n''. The lengths of the periods for various ''n'' form the so-called Pisano periods. Determining a general formula for the Pisano periods is an open problem, which includes as a subproblem a special instance of the problem of finding the multiplicative order of a modular integer or of an element in a finite field. However, for any particular ''n'', the Pisano period may be found as an instance of cycle detection.

Generalizations

The Fibonacci sequence is one of the simplest and earliest known sequences defined by a recurrence relation, and specifically by a linear difference equation. All these sequences may be viewed as generalizations of the Fibonacci sequence. In particular, Binet's formula may be generalized to any sequence that is a solution of a homogeneous linear difference equation with constant coefficients.

Some specific examples that are close, in some sense, from Fibonacci sequence include:
* Generalizing the index to negative integers to produce the negafibonacci numbers.
* Generalizing the index to real numbers using a modification of Binet's formula.
* Starting with other integers. Lucas numbers have ''L''₁ = 1, ''L''₂ = 3, and ''L_n'' = ''L''_''n''−1 + ''L''_''n''−2. Primefree sequences use the Fibonacci recursion with other starting points to generate sequences in which all numbers are composite.
* Letting a number be a linear function (other than the sum) of the 2 preceding numbers. The Pell numbers have ''P_n'' = 2''P''_{''n'' − 1} + ''P''_{''n'' − 2}. If the coefficient of the preceding value is assigned a variable value ''x'', the result is the sequence of Fibonacci polynomials.
* Not adding the immediately preceding numbers. The Padovan sequence and Perrin numbers have ''P''(''n'') = ''P''(''n'' − 2) + ''P''(''n'' − 3).
* Generating the next number by adding 3 numbers (tribonacci numbers), 4 numbers (tetranacci numbers), or more. The resulting sequences are known as ''n-Step Fibonacci numbers''.

Applications

Mathematics

The Fibonacci numbers occur in the sums of "shallow" diagonals in Pascal's triangle (see binomial coefficient):

The generating function can be expanded into
$\frac{x}{1-x-x^2} = x + x^2(1+x) + x^3(1+x)^2 + \dots + x^{k+1}(1+x)^k + \dots = \sum\limits_{n=0}^\infty F_n x^n$
and collecting like terms of $x^n$, we have the identity
$F_n = \sum_{k=0}^{\left\lfloor\frac{n-1}{2}\right\rfloor} \binom{n-k-1}{k}.$

To see how the formula is used, we can arrange the sums by the number of terms present:
:{,
,
,
, -
,
,
,
,
,
, -
,
,
,
,

which is $\binom{5}{0}+\binom{4}{1}+\binom{3}{2}$, where we are choosing the positions of ''k'' twos from ''n-k-1'' terms.

These numbers also give the solution to certain enumerative problems, the most common of which is that of counting the number of ways of writing a given number as an ordered sum of 1s and 2s (called compositions); there are ways to do this (equivalently, it's also the number of domino tilings of the $2\times n$ rectangle). For example, there are ways one can climb a staircase of 5 steps, taking one or two steps at a time:
:{,
,
,
,
,
,
,
, -
,
,
,
,

The figure shows that 8 can be decomposed into 5 (the number of ways to climb 4 steps, followed by a single-step) plus 3 (the number of ways to climb 3 steps, followed by a double-step). The same reasoning is applied recursively until a single step, of which there is only one way to climb.

The Fibonacci numbers can be found in different ways among the set of binary strings, or equivalently, among the subsets of a given set.

* The number of binary strings of length without consecutive s is the Fibonacci number . For example, out of the 16 binary strings of length 4, there are without consecutive s – they are 0000, 0001, 0010, 0100, 0101, 1000, 1001, and 1010. Such strings are the binary representations of Fibbinary numbers. Equivalently, is the number of subsets of without consecutive integers, that is, those for which for every . A bijection with the sums to ''n+1'' is to replace ''1'' with ''0'' and ''2'' with ''10'', and drop the last zero.
* The number of binary strings of length without an odd number of consecutive s is the Fibonacci number . For example, out of the 16 binary strings of length 4, there are without an odd number of consecutive s – they are 0000, 0011, 0110, 1100, 1111. Equivalently, the number of subsets of without an odd number of consecutive integers is . A bijection with the sums to ''n'' is to replace ''1'' with ''0'' and ''2'' with ''11''.
* The number of binary strings of length without an even number of consecutive s or s is . For example, out of the 16 binary strings of length 4, there are without an even number of consecutive s or s – they are 0001, 0111, 0101, 1000, 1010, 1110. There is an equivalent statement about subsets.
* Yuri Matiyasevich was able to show that the Fibonacci numbers can be defined by a Diophantine equation, which led to his solving Hilbert's tenth problem.
*The Fibonacci numbers are also an example of a complete sequence. This means that every positive integer can be written as a sum of Fibonacci numbers, where any one number is used once at most.
*Moreover, every positive integer can be written in a unique way as the sum of ''one or more'' distinct Fibonacci numbers in such a way that the sum does not include any two consecutive Fibonacci numbers. This is known as Zeckendorf's theorem, and a sum of Fibonacci numbers that satisfies these conditions is called a Zeckendorf representation. The Zeckendorf representation of a number can be used to derive its Fibonacci coding.
*Starting with 5, every second Fibonacci number is the length of the hypotenuse of a right triangle with integer sides, or in other words, the largest number in a Pythagorean triple, obtained from the formula $(F_n F_{n+3})^2 + (2 F_{n+1}F_{n+2})^2 = {F_{2 n+3^2.$ The sequence of Pythagorean triangles obtained from this formula has sides of lengths (3,4,5), (5,12,13), (16,30,34), (39,80,89), ... The middle side of each of these triangles is the sum of the three sides of the preceding triangle.
*The Fibonacci cube is an undirected graph with a Fibonacci number of nodes that has been proposed as a network topology for parallel computing.
*Fibonacci numbers appear in the ring lemma, used to prove connections between the circle packing theorem and conformal maps.

Computer science

*The Fibonacci numbers are important in computational run-time analysis of Euclid's algorithm to determine the greatest common divisor of two integers: the worst case input for this algorithm is a pair of consecutive Fibonacci numbers.
*Fibonacci numbers are used in a polyphase version of the merge sort algorithm in which an unsorted list is divided into two lists whose lengths correspond to sequential Fibonacci numbers – by dividing the list so that the two parts have lengths in the approximate proportion ''φ''. A tape-drive implementation of the polyphase merge sort was described in ''The Art of Computer Programming''.
*A Fibonacci tree is a binary tree whose child trees (recursively) differ in height by exactly 1. So it is an AVL tree, and one with the fewest nodes for a given height — the "thinnest" AVL tree. These trees have a number of vertices that is a Fibonacci number minus one, an important fact in the analysis of AVL trees.
*Fibonacci numbers are used by some pseudorandom number generators.
*Fibonacci numbers arise in the analysis of the Fibonacci heap data structure.
*A one-dimensional optimization method, called the Fibonacci search technique, uses Fibonacci numbers.
*The Fibonacci number series is used for optional lossy compression in the IFF 8SVX audio file format used on Amiga computers. The number series compands the original audio wave similar to logarithmic methods such as μ-law.
*Some Agile teams use a modified series called the "Modified Fibonacci Series" in planning poker, as an estimation tool. Planning Poker is a formal part of the Scaled Agile Framework.
* Fibonacci coding
* NegaFibonacci coding

Nature

Fibonacci sequences appear in biological settings, such as branching in trees, arrangement of leaves on a stem, the fruitlets of a pineapple, the flowering of artichoke, an uncurling fern and the arrangement of a pine cone, and the family tree of honeybees. Kepler pointed out the presence of the Fibonacci sequence in nature, using it to explain the ( golden ratio-related) pentagonal form of some flowers. Field daisies most often have petals in counts of Fibonacci numbers. In 1830, K. F. Schimper and A. Braun discovered that the parastichies (spiral phyllotaxis) of plants were frequently expressed as fractions involving Fibonacci numbers.

Przemysław Prusinkiewicz advanced the idea that real instances can in part be understood as the expression of certain algebraic constraints on free groups, specifically as certain Lindenmayer grammars.

A model for the pattern of florets in the head of a sunflower was proposed by in 1979. This has the form

$\theta = \frac{2\pi}{\varphi^2} n,\ r = c \sqrt{n}$

where is the index number of the floret and is a constant scaling factor; the florets thus lie on Fermat's spiral. The divergence angle, approximately 137.51°, is the golden angle, dividing the circle in the golden ratio. Because this ratio is irrational, no floret has a neighbor at exactly the same angle from the center, so the florets pack efficiently. Because the rational approximations to the golden ratio are of the form , the nearest neighbors of floret number are those at for some index , which depends on , the distance from the center. Sunflowers and similar flowers most commonly have spirals of florets in clockwise and counter-clockwise directions in the amount of adjacent Fibonacci numbers, typically counted by the outermost range of radii.

Fibonacci numbers also appear in the pedigrees of idealized honeybees, according to the following rules:

* If an egg is laid by an unmated female, it hatches a male or drone bee.
* If, however, an egg was fertilized by a male, it hatches a female.

Thus, a male bee always has one parent, and a female bee has two. If one traces the pedigree of any male bee (1 bee), he has 1 parent (1 bee), 2 grandparents, 3 great-grandparents, 5 great-great-grandparents, and so on. This sequence of numbers of parents is the Fibonacci sequence. The number of ancestors at each level, , is the number of female ancestors, which is , plus the number of male ancestors, which is . This is under the unrealistic assumption that the ancestors at each level are otherwise unrelated.

It has been noticed that the number of possible ancestors on the human X chromosome inheritance line at a given ancestral generation also follows the Fibonacci sequence. A male individual has an X chromosome, which he received from his mother, and a Y chromosome, which he received from his father. The male counts as the "origin" of his own X chromosome ($F_1=1$), and at his parents' generation, his X chromosome came from a single parent ($F_2=1$). The male's mother received one X chromosome from her mother (the son's maternal grandmother), and one from her father (the son's maternal grandfather), so two grandparents contributed to the male descendant's X chromosome ($F_3=2$). The maternal grandfather received his X chromosome from his mother, and the maternal grandmother received X chromosomes from both of her parents, so three great-grandparents contributed to the male descendant's X chromosome ($F_4=3$). Five great-great-grandparents contributed to the male descendant's X chromosome ($F_5=5$), etc. (This assumes that all ancestors of a given descendant are independent, but if any genealogy is traced far enough back in time, ancestors begin to appear on multiple lines of the genealogy, until eventually a population founder appears on all lines of the genealogy.)

Other

*In optics, when a beam of light shines at an angle through two stacked transparent plates of different materials of different refractive indexes, it may reflect off three surfaces: the top, middle, and bottom surfaces of the two plates. The number of different beam paths that have reflections, for , is the $k$th Fibonacci number. (However, when , there are three reflection paths, not two, one for each of the three surfaces.)
* Fibonacci retracement levels are widely used in technical analysis for financial market trading.
*Since the conversion factor 1.609344 for miles to kilometers is close to the golden ratio, the decomposition of distance in miles into a sum of Fibonacci numbers becomes nearly the kilometer sum when the Fibonacci numbers are replaced by their successors. This method amounts to a radix 2 number register in golden ratio base ''φ'' being shifted. To convert from kilometers to miles, shift the register down the Fibonacci sequence instead.
*The measured values of voltages and currents in the infinite resistor chain circuit (also called the resistor ladder or infinite series-parallel circuit) follow the Fibonacci sequence. The intermediate results of adding the alternating series and parallel resistances yields fractions composed of consecutive Fibonacci numbers. The equivalent resistance of the entire circuit equals the golden ratio.
*Brasch et al. 2012 show how a generalised Fibonacci sequence also can be connected to the field of economics. In particular, it is shown how a generalised Fibonacci sequence enters the control function of finite-horizon dynamic optimisation problems with one state and one control variable. The procedure is illustrated in an example often referred to as the Brock–Mirman economic growth model.
* Mario Merz included the Fibonacci sequence in some of his artworks beginning in 1970.
* Joseph Schillinger (1895–1943) developed a system of composition which uses Fibonacci intervals in some of its melodies; he viewed these as the musical counterpart to the elaborate harmony evident within nature. See also .

See also

*
*
*
*
*

References

Footnotes

Citations

Works cited

* .
* .
* .
*
* .
*
* .
*

External links

*

Periods of Fibonacci Sequences Mod m
at MathPages


*
*
*

{{Interwiki extra, qid=Q23835349

Articles containing proofs