Farey sequence on:
[Wikipedia]
[Google]
[Amazon]
In mathematics, the Farey sequence of order ''n'' is the sequence of completely reduced

 There is a connection between Farey sequence and Ford circles.
For every fraction (in its lowest terms) there is a Ford circle C[], which is the circle with radius 1/(2''q''2) and centre at (, ). Two Ford circles for different fractions are either Disjoint sets, disjoint or they are tangent to one another—two Ford circles never intersect. If 0 < < 1 then the Ford circles that are tangent to C[] are precisely the Ford circles for fractions that are neighbours of in some Farey sequence.
Thus ''C''[] is tangent to ''C''[], ''C''[], ''C''[], ''C''[], etc.
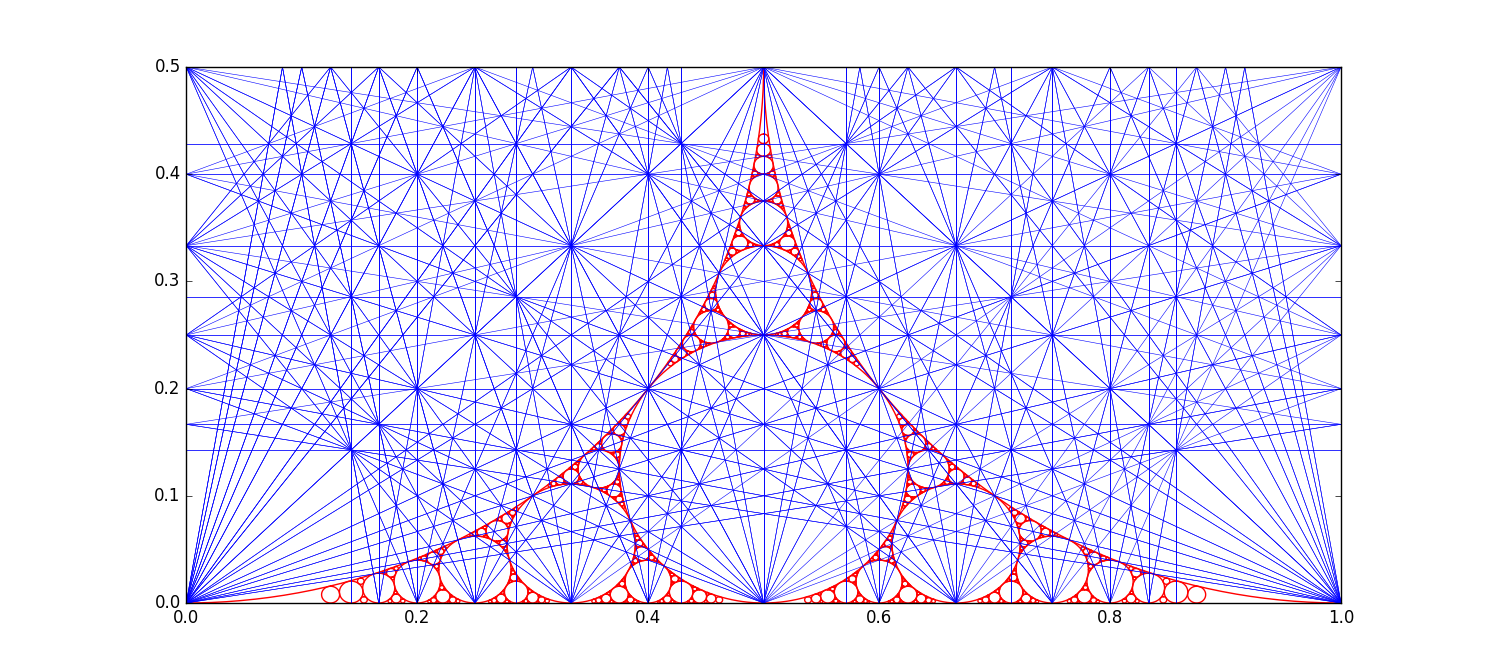
Ford circles appear also in the Apollonian gasket (0,0,1,1). The picture below illustrates this together with Farey resonance lines.
There is a connection between Farey sequence and Ford circles.
For every fraction (in its lowest terms) there is a Ford circle C[], which is the circle with radius 1/(2''q''2) and centre at (, ). Two Ford circles for different fractions are either Disjoint sets, disjoint or they are tangent to one another—two Ford circles never intersect. If 0 < < 1 then the Ford circles that are tangent to C[] are precisely the Ford circles for fractions that are neighbours of in some Farey sequence.
Thus ''C''[] is tangent to ''C''[], ''C''[], ''C''[], ''C''[], etc.
Ford circles appear also in the Apollonian gasket (0,0,1,1). The picture below illustrates this together with Farey resonance lines.
def farey_sequence(n: int, descending: bool = False) -> None:
"""Print the n'th Farey sequence. Allow for either ascending or descending."""
(a, b, c, d) = (0, 1, 1, n)
if descending:
(a, c) = (1, n - 1)
print("/".format(a, b))
while (c <= n and not descending) or (a > 0 and descending):
k = (n + b) // d
(a, b, c, d) = (c, d, k * c - a, k * d - b)
print("/".format(a, b))
Brute-force searches for solutions to Diophantine equations in rationals can often take advantage of the Farey series (to search only reduced forms). While this code uses the first two terms of the sequence to initialize ''a'', ''b'', ''c'', and ''d'', one could substitute any pair of adjacent terms in order to exclude those less than (or greater than) a particular threshold.
Errata + Code
Ghostarchive
and th
Wayback Machine
{{Authority control Fractions (mathematics) Number theory Sequences and series
fraction
A fraction (from la, fractus, "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight ...
s, either between 0 and 1, or without this restriction, which when in lowest terms
An irreducible fraction (or fraction in lowest terms, simplest form or reduced fraction) is a fraction in which the numerator and denominator are integers that have no other common divisors than 1 (and −1, when negative numbers are considered). I ...
have denominator
A fraction (from la, fractus, "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight ...
s less than or equal to ''n'', arranged in order of increasing size.
With the restricted definition, each Farey sequence starts with the value 0, denoted by the fraction , and ends with the value 1, denoted by the fraction (although some authors omit these terms).
A ''Farey sequence'' is sometimes called a Farey ''series'', which is not strictly correct, because the terms are not summed.
Examples
The Farey sequences of orders 1 to 8 are : :''F''1 = :''F''2 = :''F''3 = :''F''4 = :''F''5 = :''F''6 = :''F''7 = :''F''8 = Plotting the numerators versus the denominators of a Farey sequence gives a shape like the one to the right, shown for 6. Reflecting this shape around the diagonal and main axes generates the ''Farey sunburst'', shown below. The Farey sunburst of order connects the visible integer grid points from the origin in the square of side 2, centered at the origin. UsingPick's theorem
In geometry, Pick's theorem provides a formula for the area of a simple polygon with integer vertex coordinates, in terms of the number of integer points within it and on its boundary. The result was first described by Georg Alexander Pick i ...
the area of the sunburst is 4(, n, −1), where , n, is the number of fractions in n.
History
:''The history of 'Farey series' is very curious'' — Hardy & Wright (1979) :''... once again the man whose name was given to a mathematical relation was not the original discoverer so far as the records go.'' — Beiler (1964) Cited in Farey sequences are named after theBritish
British may refer to:
Peoples, culture, and language
* British people, nationals or natives of the United Kingdom, British Overseas Territories, and Crown Dependencies.
** Britishness, the British identity and common culture
* British English, ...
geologist
A geologist is a scientist who studies the solid, liquid, and gaseous matter that constitutes Earth and other terrestrial planets, as well as the processes that shape them. Geologists usually study geology, earth science, or geophysics, alth ...
John Farey, Sr., whose letter about these sequences was published in the ''Philosophical Magazine
The ''Philosophical Magazine'' is one of the oldest scientific journals published in English. It was established by Alexander Tilloch in 1798;John Burnett"Tilloch, Alexander (1759–1825)" Oxford Dictionary of National Biography, Oxford Unive ...
'' in 1816. Farey conjectured, without offering proof, that each new term in a Farey sequence expansion is the mediant of its neighbours. Farey's letter was read by Cauchy
Baron Augustin-Louis Cauchy (, ; ; 21 August 178923 May 1857) was a French mathematician, engineer, and physicist who made pioneering contributions to several branches of mathematics, including mathematical analysis and continuum mechanics. He w ...
, who provided a proof in his ''Exercices de mathématique'', and attributed this result to Farey. In fact, another mathematician, Charles Haros
Charles Haros was a geometer (mathematician) in the French Bureau du Cadastre at the end of the eighteenth century and the beginning of the nineteenth century.
Haros' conversion table
One of the primary tasks of the Bureau du Cadastre was the ...
, had published similar results in 1802 which were not known either to Farey or to Cauchy. Thus it was a historical accident that linked Farey's name with these sequences. This is an example of Stigler's law of eponymy
Stigler's law of eponymy, proposed by University of Chicago statistics professor Stephen Stigler in his 1980 publication ''Stigler’s law of eponymy'', states that no scientific discovery is named after its original discoverer. Examples include ...
.
Properties
Sequence length and index of a fraction
The Farey sequence of order ''n'' contains all of the members of the Farey sequences of lower orders. In particular ''Fn'' contains all of the members of ''F''''n''−1 and also contains an additional fraction for each number that is less than ''n'' andcoprime
In mathematics, two integers and are coprime, relatively prime or mutually prime if the only positive integer that is a divisor of both of them is 1. Consequently, any prime number that divides does not divide , and vice versa. This is equival ...
to ''n''. Thus ''F''6 consists of ''F''5 together with the fractions and .
The middle term of a Farey sequence ''F''''n'' is always ,
for ''n'' > 1. From this, we can relate the lengths of ''Fn'' and ''F''''n''−1 using Euler's totient function :
:
Using the fact that , ''F''1, = 2, we can derive an expression for the length of ''Fn'':
:
where is the summatory totient.
We also have :
:
and by a Möbius inversion formula :
:
where µ(''d'') is the number-theoretic Möbius function, and is the floor function.
The asymptotic behaviour of , ''Fn'', is :
:
The index of a fraction in the Farey sequence is simply the position that occupies in the sequence. This is of special relevance as it is used in an alternative formulation of the Riemann hypothesis, see below
Below may refer to:
*Earth
* Ground (disambiguation)
*Soil
*Floor
* Bottom (disambiguation)
*Less than
*Temperatures below freezing
*Hell or underworld
People with the surname
*Ernst von Below (1863–1955), German World War I general
*Fred Below ...
. Various useful properties follow:
:
:
:
:
:
The index of where and is the least common multiple of the first numbers, , is given by:
:
Farey neighbours
Fractions which are neighbouring terms in any Farey sequence are known as a ''Farey pair'' and have the following properties. If and are neighbours in a Farey sequence, with < , then their difference − is equal to . Since : this is equivalent to saying that :. Thus and are neighbours in ''F''5, and their difference is . The converse is also true. If : for positive integers ''a'',''b'',''c'' and ''d'' with ''a'' < ''b'' and ''c'' < ''d'' then and will be neighbours in the Farey sequence of order max(''b,d''). If has neighbours and in some Farey sequence, with : then is the mediant of and – in other words, : This follows easily from the previous property, since if , then , , . It follows that if and are neighbours in a Farey sequence then the first term that appears between them as the order of the Farey sequence is incremented is : which first appears in the Farey sequence of order . Thus the first term to appear between and is , which appears in ''F''8. The total number of Farey neighbour pairs in ''Fn'' is 2, ''Fn'', − 3. The '' Stern–Brocot tree'' is a data structure showing how the sequence is built up from 0 (= ) and 1 (= ), by taking successive mediants.Equivalent-area interpretation
Every consecutive pair of Farey rationals have an equivalent area of 1. See this by interpreting consecutive rationals ''r''1 = ''p''/''q'' and ''r''2 = ''p''′/''q''′ as vectors (''p'', ''q'') in the x–y plane. The area of ''A''(''p''/''q'', ''p''′/''q''′) is given by ''qp''′ − ''q''′''p''. As any added fraction in between two previous consecutive Farey sequence fractions is calculated as the mediant (⊕), then ''A''(''r''1, ''r''1 ⊕ ''r''2) = ''A''(''r''1, ''r''1) + ''A''(''r''1, ''r''2) = ''A''(''r''1, ''r''2) = 1 (since ''r''1 = 1/0 and ''r''2 = 0/1, its area must be 1).Farey neighbours and continued fractions
Fractions that appear as neighbours in a Farey sequence have closely relatedcontinued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer ...
expansions. Every fraction has two continued fraction expansions — in one the final term is 1; in the other the final term is greater than 1. If , which first appears in Farey sequence ''Fq'', has continued fraction expansions
: ; ''a''1, ''a''2, ..., ''a''''n'' − 1, ''a''''n'', 1: ; ''a''1, ''a''2, ..., ''a''''n'' − 1, ''a''''n'' + 1
then the nearest neighbour of in ''Fq'' (which will be its neighbour with the larger denominator) has a continued fraction expansion
: ; ''a''1, ''a''2, ..., ''a''''n''
and its other neighbour has a continued fraction expansion
: ; ''a''1, ''a''2, ..., ''a''''n'' − 1
For example, has the two continued fraction expansions and , and its neighbours in ''F''8 are , which can be expanded as ; and , which can be expanded as .
Farey fractions and the least common multiple
The lcm can be expressed as the products of Farey fractions as : where is the secondChebyshev function
In mathematics, the Chebyshev function is either a scalarising function (Tchebycheff function) or one of two related functions. The first Chebyshev function or is given by
:\vartheta(x)=\sum_ \ln p
where \ln denotes the natural logarithm, ...
.
Farey fractions and the greatest common divisor
Since the Euler's totient function is directly connected to the gcd so is the number of elements in ''Fn'', : For any 3 Farey fractions , and the following identity between the gcd's of the 2x2matrix determinant
In mathematics, the determinant is a scalar value that is a function of the entries of a square matrix. It characterizes some properties of the matrix and the linear map represented by the matrix. In particular, the determinant is nonzero if an ...
s in absolute value holds:
:
Applications
Farey sequences are very useful to find rational approximations of irrational numbers. For example, the construction by Eliahou of a lower bound on the length of non-trivial cycles in the 3''x''+1 process uses Farey sequences to calculate a continued fraction expansion of the number log2(3). In physical systems with resonance phenomena, Farey sequences provide a very elegant and efficient method to compute resonance locations in 1D and 2D. Farey sequences are prominent in studies of any-angle path planning on square-celled grids, for example in characterizing their computational complexity or optimality. The connection can be considered in terms of ''r''-constrained paths, namely paths made up of line segments that each traverse at most rows and at most columns of cells. Let be the set of vectors such that , , and , are coprime. Let be the result of reflecting in the line . Let . Then any ''r''-constrained path can be described as a sequence of vectors from . There is a bijection between and the Farey sequence of order given by mapping to .Ford circles

Riemann hypothesis
Farey sequences are used in two equivalent formulations of the Riemann hypothesis. Suppose the terms of are . Define , in other words is the difference between the ''k''th term of the ''n''th Farey sequence, and the ''k''th member of a set of the same number of points, distributed evenly on the unit interval. In 1924 Jérôme Franel proved that the statement : is equivalent to the Riemann hypothesis, and then Edmund Landau remarked (just after Franel's paper) that the statement : is also equivalent to the Riemann hypothesis.Other sums involving Farey fractions
The sum of all Farey fractions of order ''n'' is half the number of elements: : The sum of the denominators in the Farey sequence is twice the sum of the numerators and relates to Euler's totient function: : which was conjectured by Harold L. Aaron in 1962 and demonstrated by Jean A. Blake in 1966. A one line proof of the Harold L. Aaron conjecture is as follows. The sum of the numerators is . The sum of denominators is . The quotient of the first sum by the second sum is . Let ''b''''j'' be the ordered denominators of ''F''''n'', then: : and : Let ''a''''j''/''b''''j'' the ''j''th Farey fraction in ''F''''n'', then : which is demonstrated in. Also according to this reference the term inside the sum can be expressed in many different ways: : obtaining thus many different sums over the Farey elements with same result. Using the symmetry around 1/2 the former sum can be limited to half of the sequence as : The Mertens function can be expressed as a sum over Farey fractions as : where is the Farey sequence of order ''n''. This formula is used in the proof of the Franel–Landau theorem.Next term
A surprisingly simple algorithm exists to generate the terms of ''Fn'' in either traditional order (ascending) or non-traditional order (descending). The algorithm computes each successive entry in terms of the previous two entries using the mediant property given above. If and are the two given entries, and is the unknown next entry, then = . Since is in lowest terms, there must be an integer ''k'' such that ''kc'' = ''a'' + ''p'' and ''kd'' = ''b'' + ''q'', giving ''p'' = ''kc'' − ''a'' and ''q'' = ''kd'' − ''b''. If we consider ''p'' and ''q'' to be functions of ''k'', then : so the larger ''k'' gets, the closer gets to . To give the next term in the sequence ''k'' must be as large as possible, subject to ''kd'' − ''b'' ≤ ''n'' (as we are only considering numbers with denominators not greater than ''n''), so ''k'' is the greatest integer ≤ . Putting this value of ''k'' back into the equations for ''p'' and ''q'' gives : : This is implemented inPython
Python may refer to:
Snakes
* Pythonidae, a family of nonvenomous snakes found in Africa, Asia, and Australia
** ''Python'' (genus), a genus of Pythonidae found in Africa and Asia
* Python (mythology), a mythical serpent
Computing
* Python (pr ...
as follows:
See also
*ABACABA pattern
The ABACABA pattern is a recursive fractal pattern that shows up in many places in the real world (such as in geometry, art, music, poetry, number systems, literature and higher dimensions). Patterns often show a DABACABA type subset. ''AA'', ' ...
* Stern–Brocot tree
* Euler's totient function
Footnotes
References
Further reading
* * — in particular, see §4.5 (pp. 115–123), Bonus Problem 4.61 (pp. 150, 523–524), §4.9 (pp. 133–139), §9.3, Problem 9.3.6 (pp. 462–463). * — reviews the isomorphisms of the Stern-Brocot Tree. * — reviews connections between Farey Fractions and Fractals. * *Errata + Code
External links
* * * * * * * * * Archived aGhostarchive
and th
Wayback Machine
{{Authority control Fractions (mathematics) Number theory Sequences and series