Fair Coin on:
[Wikipedia]
[Google]
[Amazon]
In
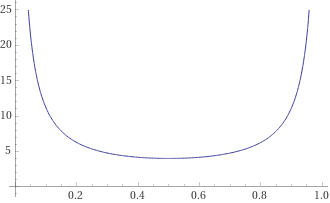 The more biased our coin is, the more likely it is that we will have to perform a greater number of trials before a fair result.
The more biased our coin is, the more likely it is that we will have to perform a greater number of trials before a fair result.
Available
from Andrew Gelman's website *{{cite news, title=Lifelong debunker takes on arbiter of neutral choices: Magician-turned-mathematician uncovers bias in a flip of a coin , url=http://news-service.stanford.edu/news/2004/june9/diaconis-69.html , work=Stanford Report, date= 2004-06-07 , access-date=2008-03-05 *John von Neumann, "Various techniques used in connection with random digits," in A.S. Householder, G.E. Forsythe, and H.H. Germond, eds., ''Monte Carlo Method'', National Bureau of Standards Applied Mathematics Series, 12 (Washington, D.C.: U.S. Government Printing Office, 1951): 36-38. Experiment (probability theory) Gambling mathematics Coin flipping
probability theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expre ...
and statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ...
, a sequence of independent
Independent or Independents may refer to:
Arts, entertainment, and media Artist groups
* Independents (artist group), a group of modernist painters based in Pennsylvania, United States
* Independentes (English: Independents), a Portuguese artist ...
Bernoulli trial
In the theory of probability and statistics, a Bernoulli trial (or binomial trial) is a random experiment with exactly two possible outcomes, "success" and "failure", in which the probability of success is the same every time the experiment is ...
s with probability 1/2 of success on each trial is metaphorically called a fair coin. One for which the probability is not 1/2 is called a biased or unfair coin. In theoretical studies, the assumption that a coin is fair is often made by referring to an ideal coin.
John Edmund Kerrich performed experiments in coin flipping and found that a coin made from a wooden disk about the size of a crown and coated on one side with lead
Lead () is a chemical element; it has Chemical symbol, symbol Pb (from Latin ) and atomic number 82. It is a Heavy metal (elements), heavy metal that is density, denser than most common materials. Lead is Mohs scale, soft and Ductility, malleabl ...
landed heads (wooden side up) 679 times out of 1000. In this experiment the coin was tossed by balancing it on the forefinger, flipping it using the thumb so that it spun through the air for about a foot before landing on a flat cloth spread over a table. Edwin Thompson Jaynes
Edwin Thompson Jaynes (July 5, 1922 – April 30, 1998) was the Wayman Crow Distinguished Professor of Physics at Washington University in St. Louis. He wrote extensively on statistical mechanics and on foundations of probability and statistic ...
claimed that when a coin is caught in the hand, instead of being allowed to bounce, the physical bias in the coin is insignificant compared to the method of the toss, where with sufficient practice a coin can be made to land heads 100% of the time. Exploring the problem of checking whether a coin is fair is a well-established pedagogical tool in teaching statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ...
.
Probability space definition
Inprobability theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expre ...
, a fair coin is defined as a probability space
In probability theory, a probability space or a probability triple (\Omega, \mathcal, P) is a mathematical construct that provides a formal model of a random process or "experiment". For example, one can define a probability space which models ...
, which is in turn defined by the sample space
In probability theory, the sample space (also called sample description space, possibility space, or outcome space) of an experiment or random trial is the set of all possible outcomes or results of that experiment. A sample space is usually den ...
, event space
Event may refer to:
Gatherings of people
* Ceremony, an event of ritual significance, performed on a special occasion
* Convention (meeting), a gathering of individuals engaged in some common interest
* Event management, the organization of e ...
, and probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a σ-algebra that satisfies Measure (mathematics), measure properties such as ''countable additivity''. The difference between a probability measure an ...
. Using for heads and for tails, the sample space of a coin is defined as:
The event space for a coin includes all sets of outcomes from the sample space which can be assigned a probability, which is the full power set
In mathematics, the power set (or powerset) of a set is the set of all subsets of , including the empty set and itself. In axiomatic set theory (as developed, for example, in the ZFC axioms), the existence of the power set of any set is po ...
. Thus, the event space is defined as:
is the event where neither outcome happens (which is impossible and can therefore be assigned 0 probability), and is the event where either outcome happens, (which is guaranteed and can be assigned 1 probability). Because the coin is fair, the possibility of any single outcome is 50-50. The probability measure is then defined by the function:
So the full probability space which defines a fair coin is the triplet as defined above. Note that this is not a random variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a Mathematics, mathematical formalization of a quantity or object which depends on randomness, random events. The term 'random variable' in its mathema ...
because heads and tails do not have inherent numerical values like you might find on a fair two-valued die. A random variable adds the additional structure of assigning a numerical value to each outcome. Common choices are or .
Role in statistical teaching and theory
The probabilistic and statistical properties of coin-tossing games are often used as examples in both introductory and advanced text books and these are mainly based in assuming that a coin is fair or "ideal". For example, Feller uses this basis to introduce both the idea ofrandom walk
In mathematics, a random walk, sometimes known as a drunkard's walk, is a stochastic process that describes a path that consists of a succession of random steps on some Space (mathematics), mathematical space.
An elementary example of a rand ...
s and to develop tests for homogeneity
Homogeneity and heterogeneity are concepts relating to the Uniformity (chemistry), uniformity of a Chemical substance, substance, process or image. A homogeneous feature is uniform in composition or character (i.e., color, shape, size, weight, ...
within a sequence of observations by looking at the properties of the runs of identical values within a sequence. The latter leads on to a runs test. A time-series consisting of the result from tossing a fair coin is called a Bernoulli process
In probability and statistics, a Bernoulli process (named after Jacob Bernoulli) is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1. The ...
.
Fair results from a biased coin
If a cheat has altered a coin to prefer one side over another (a biased coin), the coin can still be used for fair results by changing the game slightly.John von Neumann
John von Neumann ( ; ; December 28, 1903 – February 8, 1957) was a Hungarian and American mathematician, physicist, computer scientist and engineer. Von Neumann had perhaps the widest coverage of any mathematician of his time, in ...
gave the following procedure:
# Toss the coin twice.
# If the results match, start over, forgetting both results.
# If the results differ, use the first result, forgetting the second.
The reason this process produces a fair result is that the probability of getting heads and then tails must be the same as the probability of getting tails and then heads, as the coin is not changing its bias between flips and the two flips are independent. This works only if getting one result on a trial does not change the bias on subsequent trials, which is the case for most non-malleable
Ductility refers to the ability of a material to sustain significant plastic deformation before fracture. Plastic deformation is the permanent distortion of a material under applied stress, as opposed to elastic deformation, which is reversi ...
coins (but ''not'' for processes such as the Pólya urn). By excluding the events of two heads and two tails by repeating the procedure, the coin flipper is left with the only two remaining outcomes having equivalent probability. This procedure ''only'' works if the tosses are paired properly; if part of a pair is reused in another pair, the fairness may be ruined. Also, the coin must not be so biased that one side has a probability of zero.
This method may be extended by also considering sequences of four tosses. That is, if the coin is flipped twice but the results match, and the coin is flipped twice again but the results match now for the opposite side, then the first result can be used. This is because HHTT and TTHH are equally likely. This can be extended to any multiple of 2.
The expected value of flips at the n game is not hard to calculate, first notice that in step 3 whatever the event or we have flipped the coin twice so but in step 2 ( or ) we also have to redo things so we will have 2 flips plus the expected value of flips of the next game that is but as we start over the expected value of the next game is the same as the value of the previous game or any other game so it does not really depend on n thus (this can be understood the process being a martingale where taking the expectation again get us that but because of the law of total expectation
The proposition in probability theory known as the law of total expectation, the law of iterated expectations (LIE), Adam's law, the tower rule, and the smoothing property of conditional expectation, among other names, states that if X is a random ...
we get that ) hence we have:
 The more biased our coin is, the more likely it is that we will have to perform a greater number of trials before a fair result.
The more biased our coin is, the more likely it is that we will have to perform a greater number of trials before a fair result.
A better algorithm when ''P''(H) is known
Suppose that the bias is known. In this section, we provide a simple algorithmHenry Tsai, 2024 April 12. that improves the expected number of coin tosses. The algorithm allows simulating a coin with any probability , and the value of changes internally across iterations. To get a fair coin, the algorithm first sets and then executes the following steps. # Toss the biased coin. Let be the result. # If , use if the flip result is . Otherwise, set to and go back to step 1. # Otherwise, , use if the flip result is . Otherwise, set to and go back to step 1. Note that the above algorithm does not reach the optimal expected number of coin tosses, which is (here is thebinary entropy function
Binary may refer to:
Science and technology Mathematics
* Binary number, a representation of numbers using only two values (0 and 1) for each digit
* Binary function, a function that takes two arguments
* Binary operation, a mathematical op ...
).
There are algorithms that reach this optimal value in expectation. However, those algorithms are more sophisticated than the one above.
The above algorithm has an expected number of biased coinflips being , which is exactly half of the expected flips for von Neumann's approach.
Analysis
The correctness of the above algorithm is a perfect exercise of conditional expectation. We now analyze the expected number of coinflips. Given the bias and the current value of , one can define a function that represents the expected number of coin tosses before a result is returned. The recurrence relation of can be described as follows. This solves to the following function: When , the expected number of coinflips is as desired.See also
* Checking whether a coin is fair * Coin flipping * Feller's coin-tossing constantsReferences
Further reading
Available
from Andrew Gelman's website *{{cite news, title=Lifelong debunker takes on arbiter of neutral choices: Magician-turned-mathematician uncovers bias in a flip of a coin , url=http://news-service.stanford.edu/news/2004/june9/diaconis-69.html , work=Stanford Report, date= 2004-06-07 , access-date=2008-03-05 *John von Neumann, "Various techniques used in connection with random digits," in A.S. Householder, G.E. Forsythe, and H.H. Germond, eds., ''Monte Carlo Method'', National Bureau of Standards Applied Mathematics Series, 12 (Washington, D.C.: U.S. Government Printing Office, 1951): 36-38. Experiment (probability theory) Gambling mathematics Coin flipping