Euclidean metric on:
[Wikipedia]
[Google]
[Amazon]
 In
In
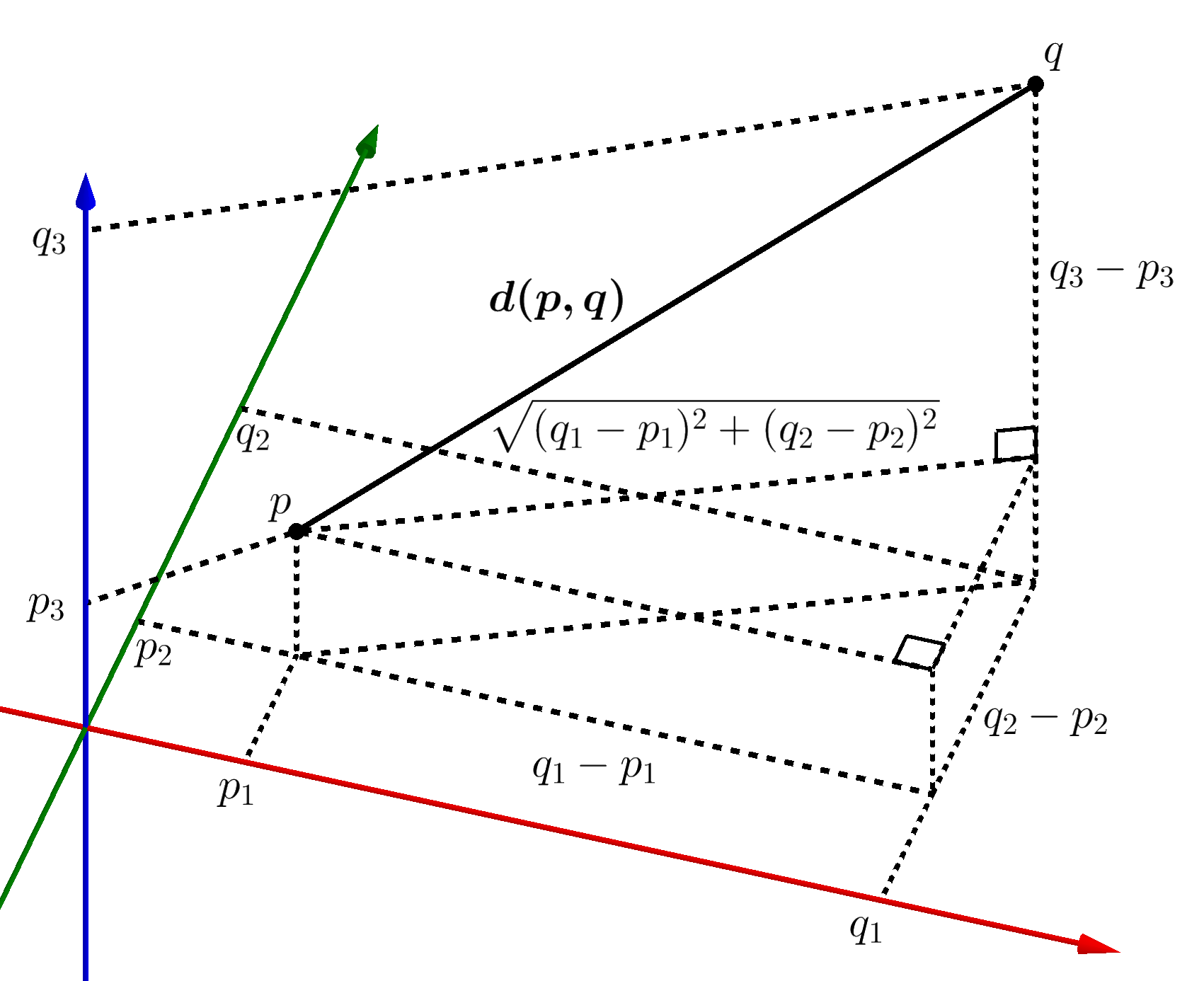 In three dimensions, for points given by their Cartesian coordinates, the distance is
In general, for points given by Cartesian coordinates in -dimensional Euclidean space, the distance is
The Euclidean distance may also be expressed more compactly in terms of the Euclidean norm of the
In three dimensions, for points given by their Cartesian coordinates, the distance is
In general, for points given by Cartesian coordinates in -dimensional Euclidean space, the distance is
The Euclidean distance may also be expressed more compactly in terms of the Euclidean norm of the
 Other common distances in
Other common distances in
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, the Euclidean distance between two points in Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
is the length
Length is a measure of distance. In the International System of Quantities, length is a quantity with Dimension (physical quantity), dimension distance. In most systems of measurement a Base unit (measurement), base unit for length is chosen, ...
of the line segment
In geometry, a line segment is a part of a line (mathematics), straight line that is bounded by two distinct endpoints (its extreme points), and contains every Point (geometry), point on the line that is between its endpoints. It is a special c ...
between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
, and therefore is occasionally called the Pythagorean distance.
These names come from the ancient Greek mathematicians Euclid
Euclid (; ; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the '' Elements'' treatise, which established the foundations of geometry that largely domina ...
and Pythagoras
Pythagoras of Samos (; BC) was an ancient Ionian Greek philosopher, polymath, and the eponymous founder of Pythagoreanism. His political and religious teachings were well known in Magna Graecia and influenced the philosophies of P ...
. In the Greek deductive
Deductive reasoning is the process of drawing valid inferences. An inference is valid if its conclusion follows logically from its premises, meaning that it is impossible for the premises to be true and the conclusion to be false. For example, th ...
geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
exemplified by Euclid's ''Elements'', distances were not represented as numbers but line segments of the same length, which were considered "equal". The notion of distance is inherent in the compass
A compass is a device that shows the cardinal directions used for navigation and geographic orientation. It commonly consists of a magnetized needle or other element, such as a compass card or compass rose, which can pivot to align itself with No ...
tool used to draw a circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
, whose points all have the same distance from a common center point. The connection from the Pythagorean theorem to distance calculation was not made until the 18th century.
The distance between two objects that are not points is usually defined to be the smallest distance among pairs of points from the two objects. Formulas are known for computing distances between different types of objects, such as the distance from a point to a line. In advanced mathematics, the concept of distance has been generalized to abstract metric space
In mathematics, a metric space is a Set (mathematics), set together with a notion of ''distance'' between its Element (mathematics), elements, usually called point (geometry), points. The distance is measured by a function (mathematics), functi ...
s, and other distances than Euclidean have been studied. In some applications in statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ...
and optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfiel ...
, the square of the Euclidean distance is used instead of the distance itself.
Distance formulas
One dimension
The distance between any two points on thereal line
A number line is a graphical representation of a straight line that serves as spatial representation of numbers, usually graduated like a ruler with a particular origin (geometry), origin point representing the number zero and evenly spaced mark ...
is the absolute value
In mathematics, the absolute value or modulus of a real number x, is the non-negative value without regard to its sign. Namely, , x, =x if x is a positive number, and , x, =-x if x is negative (in which case negating x makes -x positive), ...
of the numerical difference of their coordinates, their absolute difference. Thus if and are two points on the real line, then the distance between them is given by:
A more complicated formula, giving the same value, but generalizing more readily to higher dimensions, is:
In this formula, squaring and then taking the square root
In mathematics, a square root of a number is a number such that y^2 = x; in other words, a number whose ''square'' (the result of multiplying the number by itself, or y \cdot y) is . For example, 4 and −4 are square roots of 16 because 4 ...
leaves any positive number unchanged, but replaces any negative number by its absolute value.
Two dimensions
In theEuclidean plane
In mathematics, a Euclidean plane is a Euclidean space of Two-dimensional space, dimension two, denoted \textbf^2 or \mathbb^2. It is a geometric space in which two real numbers are required to determine the position (geometry), position of eac ...
, let point have Cartesian coordinates
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...
and let point have coordinates . Then the distance between and is given by:
This can be seen by applying the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
to a right triangle with horizontal and vertical sides, having the line segment from to as its hypotenuse. The two squared formulas inside the square root give the areas of squares on the horizontal and vertical sides, and the outer square root converts the area of the square on the hypotenuse into the length of the hypotenuse. In terms of the Pythagorean addition operation , available in many software libraries as hypot, the same formula can be expressed as:
It is also possible to compute the distance for points given by polar coordinates
In mathematics, the polar coordinate system specifies a given point (mathematics), point in a plane (mathematics), plane by using a distance and an angle as its two coordinate system, coordinates. These are
*the point's distance from a reference ...
. If the polar coordinates of are and the polar coordinates of are , then their distance is given by the law of cosines
In trigonometry, the law of cosines (also known as the cosine formula or cosine rule) relates the lengths of the sides of a triangle to the cosine of one of its angles. For a triangle with sides , , and , opposite respective angles , , and (see ...
:
When and are expressed as complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s in the complex plane
In mathematics, the complex plane is the plane (geometry), plane formed by the complex numbers, with a Cartesian coordinate system such that the horizontal -axis, called the real axis, is formed by the real numbers, and the vertical -axis, call ...
, the same formula for one-dimensional points expressed as real numbers can be used, although here the absolute value sign indicates the complex norm:
Higher dimensions
 In three dimensions, for points given by their Cartesian coordinates, the distance is
In general, for points given by Cartesian coordinates in -dimensional Euclidean space, the distance is
The Euclidean distance may also be expressed more compactly in terms of the Euclidean norm of the
In three dimensions, for points given by their Cartesian coordinates, the distance is
In general, for points given by Cartesian coordinates in -dimensional Euclidean space, the distance is
The Euclidean distance may also be expressed more compactly in terms of the Euclidean norm of the Euclidean vector
In mathematics, physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector or spatial vector) is a geometric object that has magnitude (or length) and direction. Euclidean vectors can be added and scal ...
difference:
Objects other than points
For pairs of objects that are not both points, the distance can most simply be defined as the smallest distance between any two points from the two objects, although more complicated generalizations from points to sets such as Hausdorff distance are also commonly used. Formulas for computing distances between different types of objects include: *The distance from a point to a line, in the Euclidean plane *The distance from a point to a plane in three-dimensional Euclidean space *The distance between two lines in three-dimensional Euclidean space The distance from a point to acurve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...
can be used to define its parallel curve, another curve all of whose points have the same distance to the given curve.
Properties
The Euclidean distance is the prototypical example of the distance in ametric space
In mathematics, a metric space is a Set (mathematics), set together with a notion of ''distance'' between its Element (mathematics), elements, usually called point (geometry), points. The distance is measured by a function (mathematics), functi ...
, and obeys all the defining properties of a metric space:
*It is ''symmetric'', meaning that for all points and , . That is (unlike road distance with one-way streets) the distance between two points does not depend on which of the two points is the start and which is the destination.
*It is ''positive'', meaning that the distance between every two distinct points is a positive number
In mathematics, the sign of a real number is its property of being either positive, negative, or 0. Depending on local conventions, zero may be considered as having its own unique sign, having no sign, or having both positive and negative sign. ...
, while the distance from any point to itself is zero.
*It obeys the triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side.
This statement permits the inclusion of Degeneracy (mathematics)#T ...
: for every three points , , and , . Intuitively, traveling from to via cannot be any shorter than traveling directly from to .
Another property, Ptolemy's inequality, concerns the Euclidean distances among four points , , , and . It states that
For points in the plane, this can be rephrased as stating that for every quadrilateral
In Euclidean geometry, geometry a quadrilateral is a four-sided polygon, having four Edge (geometry), edges (sides) and four Vertex (geometry), corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''l ...
, the products of opposite sides of the quadrilateral sum to at least as large a number as the product of its diagonals. However, Ptolemy's inequality applies more generally to points in Euclidean spaces of any dimension, no matter how they are arranged. For points in metric spaces that are not Euclidean spaces, this inequality may not be true. Euclidean distance geometry studies properties of Euclidean distance such as Ptolemy's inequality, and their application in testing whether given sets of distances come from points in a Euclidean space.
According to the Beckman–Quarles theorem, any transformation of the Euclidean plane or of a higher-dimensional Euclidean space that preserves unit distances must be an isometry
In mathematics, an isometry (or congruence, or congruent transformation) is a distance-preserving transformation between metric spaces, usually assumed to be bijective. The word isometry is derived from the Ancient Greek: ἴσος ''isos'' me ...
, preserving all distances.
Squared Euclidean distance
In many applications, and in particular when comparing distances, it may be more convenient to omit the final square root in the calculation of Euclidean distances, as the square root does not change the order ( if and only if ). The value resulting from this omission is thesquare
In geometry, a square is a regular polygon, regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal si ...
of the Euclidean distance, and is called the squared Euclidean distance. For instance, the Euclidean minimum spanning tree can be determined using only the ordering between distances, and not their numeric values. Comparing squared distances produces the same result but avoids an unnecessary square-root calculation and sidesteps issues of numerical precision. As an equation, the squared distance can be expressed as a sum of squares:
Beyond its application to distance comparison, squared Euclidean distance is of central importance in statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ...
, where it is used in the method of least squares, a standard method of fitting statistical estimates to data by minimizing the average of the squared distances between observed and estimated values, and as the simplest form of divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the rate that the vector field alters the volume in an infinitesimal neighborhood of each point. (In 2D this "volume" refers to ...
to compare probability distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical descri ...
s. The addition of squared distances to each other, as is done in least squares fitting, corresponds to an operation on (unsquared) distances called Pythagorean addition. In cluster analysis
Cluster analysis or clustering is the data analyzing technique in which task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more Similarity measure, similar (in some specific sense defined by the ...
, squared distances can be used to strengthen the effect of longer distances.
Squared Euclidean distance does not form a metric space, as it does not satisfy the triangle inequality. However it is a smooth, strictly convex function
In mathematics, a real-valued function is called convex if the line segment between any two distinct points on the graph of a function, graph of the function lies above or on the graph between the two points. Equivalently, a function is conve ...
of the two points, unlike the distance, which is non-smooth (near pairs of equal points) and convex but not strictly convex. The squared distance is thus preferred in optimization theory, since it allows convex analysis
Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex optimization, convex minimization, a subdomain of optimization (mathematics), optimization theor ...
to be used. Since squaring is a monotonic function
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of or ...
of non-negative values, minimizing squared distance is equivalent to minimizing the Euclidean distance, so the optimization problem is equivalent in terms of either, but easier to solve using squared distance.
The collection of all squared distances between pairs of points from a finite set may be stored in a Euclidean distance matrix, and is used in this form in distance geometry.
Generalizations
In more advanced areas of mathematics, when viewing Euclidean space as avector space
In mathematics and physics, a vector space (also called a linear space) is a set (mathematics), set whose elements, often called vector (mathematics and physics), ''vectors'', can be added together and multiplied ("scaled") by numbers called sc ...
, its distance is associated with a norm called the Euclidean norm, defined as the distance of each vector from the origin. One of the important properties of this norm, relative to other norms, is that it remains unchanged under arbitrary rotations of space around the origin. By Dvoretzky's theorem, every finite-dimensional normed vector space has a high-dimensional subspace on which the norm is approximately Euclidean; the Euclidean norm is the
only norm with this property. It can be extended to infinite-dimensional vector spaces as the norm or distance. The Euclidean distance gives Euclidean space the structure of a topological space
In mathematics, a topological space is, roughly speaking, a Geometry, geometrical space in which Closeness (mathematics), closeness is defined but cannot necessarily be measured by a numeric Distance (mathematics), distance. More specifically, a to ...
, the Euclidean topology
In mathematics, and especially general topology, the Euclidean topology is the natural topology induced on n-dimensional Euclidean space \R^n by the Euclidean metric.
Definition
The Euclidean norm on \R^n is the non-negative function \, \cdot ...
, with the open balls (subsets of points at less than a given distance from a given point) as its neighborhoods.
real coordinate space
In mathematics, the real coordinate space or real coordinate ''n''-space, of dimension , denoted or , is the set of all ordered -tuples of real numbers, that is the set of all sequences of real numbers, also known as '' coordinate vectors''.
...
s and function space
In mathematics, a function space is a set of functions between two fixed sets. Often, the domain and/or codomain will have additional structure which is inherited by the function space. For example, the set of functions from any set into a ve ...
s:
* Chebyshev distance ( distance), which measures distance as the maximum of the distances in each coordinate.
* Taxicab distance ( distance), also called Manhattan distance, which measures distance as the sum of the distances in each coordinate.
* Minkowski distance ( distance), a generalization that unifies Euclidean distance, taxicab distance, and Chebyshev distance.
For points on surfaces in three dimensions, the Euclidean distance should be distinguished from the geodesic distance, the length of a shortest curve that belongs to the surface. In particular, for measuring great-circle distances on the Earth or other spherical or near-spherical surfaces, distances that have been used include the haversine distance giving great-circle distances between two points on a sphere from their longitudes and latitudes, and Vincenty's formulae also known as "Vincent distance" for distance on a spheroid.
History
Euclidean distance is the distance inEuclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
. Both concepts are named after ancient Greek mathematician Euclid
Euclid (; ; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the '' Elements'' treatise, which established the foundations of geometry that largely domina ...
, whose ''Elements'' became a standard textbook in geometry for many centuries. Concepts of length
Length is a measure of distance. In the International System of Quantities, length is a quantity with Dimension (physical quantity), dimension distance. In most systems of measurement a Base unit (measurement), base unit for length is chosen, ...
and distance
Distance is a numerical or occasionally qualitative measurement of how far apart objects, points, people, or ideas are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria (e.g. "two co ...
are widespread across cultures, can be dated to the earliest surviving "protoliterate" bureaucratic documents from Sumer
Sumer () is the earliest known civilization, located in the historical region of southern Mesopotamia (now south-central Iraq), emerging during the Chalcolithic and Early Bronze Age, early Bronze Ages between the sixth and fifth millennium BC. ...
in the fourth millennium BC (far before Euclid), and have been hypothesized to develop in children earlier than the related concepts of speed and time. But the notion of a distance, as a number defined from two points, does not actually appear in Euclid's ''Elements''. Instead, Euclid approaches this concept implicitly, through the congruence of line segments, through the comparison of lengths of line segments, and through the concept of proportionality.
The Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
is also ancient, but it could only take its central role in the measurement of distances after the invention of Cartesian coordinates
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...
by René Descartes
René Descartes ( , ; ; 31 March 1596 – 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and Modern science, science. Mathematics was paramou ...
in 1637. The distance formula itself was first published in 1731 by Alexis Clairaut. Because of this formula, Euclidean distance is also sometimes called Pythagorean distance. Although accurate measurements of long distances on the Earth's surface, which are not Euclidean, had again been studied in many cultures since ancient times (see history of geodesy), the idea that Euclidean distance might not be the only way of measuring distances between points in mathematical spaces came even later, with the 19th-century formulation of non-Euclidean geometry. The definition of the Euclidean norm and Euclidean distance for geometries of more than three dimensions also first appeared in the 19th century, in the work of Augustin-Louis Cauchy
Baron Augustin-Louis Cauchy ( , , ; ; 21 August 1789 – 23 May 1857) was a French mathematician, engineer, and physicist. He was one of the first to rigorously state and prove the key theorems of calculus (thereby creating real a ...
.
References
{{Authority control, state=collapsed Distance Length Metric geometry Pythagorean theoremdistance
Distance is a numerical or occasionally qualitative measurement of how far apart objects, points, people, or ideas are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria (e.g. "two co ...