effective potential

The effective potential (also known as effective potential energy) combines multiple, perhaps opposing, effects into a single potential. In its basic form, it is the sum of the "opposing" centrifugal potential energy with the potential energy of a dynamical system. It may be used to determine the orbits of planets (both Newtonian and relativistic) and to perform semi-classical atomic calculations, and often allows problems to be reduced to fewer dimensions.

Definition

The basic form of potential $U_\text$ is defined as
$U_\text(\mathbf) = \frac + U(\mathbf),$
where
: ''L'' is the angular momentum,
: ''r'' is the distance between the two masses,
: ''μ'' is the reduced mass of the two bodies (approximately equal to the mass of the orbiting body if one mass is much larger than the other),
: ''U''(''r'') is the general form of the potential.

The effective force, then, is the negative gradient of the effective potential:
$\begin \mathbf_\text &= -\nabla U_\text(\mathbf) \\ &= \frac \hat - \nabla U(\mathbf), \end$
where $\hat$ denotes a unit vector in the radial direction.

Important properties

There are many useful features of the effective potential, such as
$U_\text \leq E.$

To find the radius of a circular orbit, simply minimize the effective potential with respect to $r$, or equivalently set the net force to zero and then solve for $r_0$:
$\frac = 0.$
After solving for $r_0$, plug this back into $U_\text$ to find the maximum value of the effective potential $U_\text^\text$.

A circular orbit may be either stable or unstable. If it is unstable, a small perturbation could destabilize the orbit, but a stable orbit would return to equilibrium. To determine the stability of a circular orbit, determine the concavity of the effective potential. If the concavity is positive,
$\frac > 0,$
the orbit is stable.

The frequency of small oscillations, using basic Hamiltonian analysis, is
$\omega = \sqrt,$
where the double prime indicates the second derivative of the effective potential with respect to $r$ and is evaluated at a minimum.

Gravitational potential

Consider a particle of mass ''m'' orbiting a much heavier object of mass ''M''. Assume Newtonian mechanics, which is both classical and non-relativistic. The conservation of energy and angular momentum give two constants ''E'' and ''L'', which have values
$E = \fracm \left(\dot^2 + r^2\dot^2\right) - \frac,$
$L = mr^2\dot,$
when the motion of the larger mass is negligible. In these expressions,
: $\dot$ is the derivative of ''r'' with respect to time,
: $\dot$ is the angular velocity of mass ''m'',
: ''G'' is the gravitational constant,
: ''E'' is the total energy,
: ''L'' is the angular momentum.

Only two variables are needed, since the motion occurs in a plane. Substituting the second expression into the first and rearranging gives
$m\dot^2 = 2E - \frac + \frac = 2E - \frac \left(\frac - 2GmMr\right),$
$\frac m \dot^2 = E - U_\text(r),$
where
$U_\text(r) = \frac - \frac$
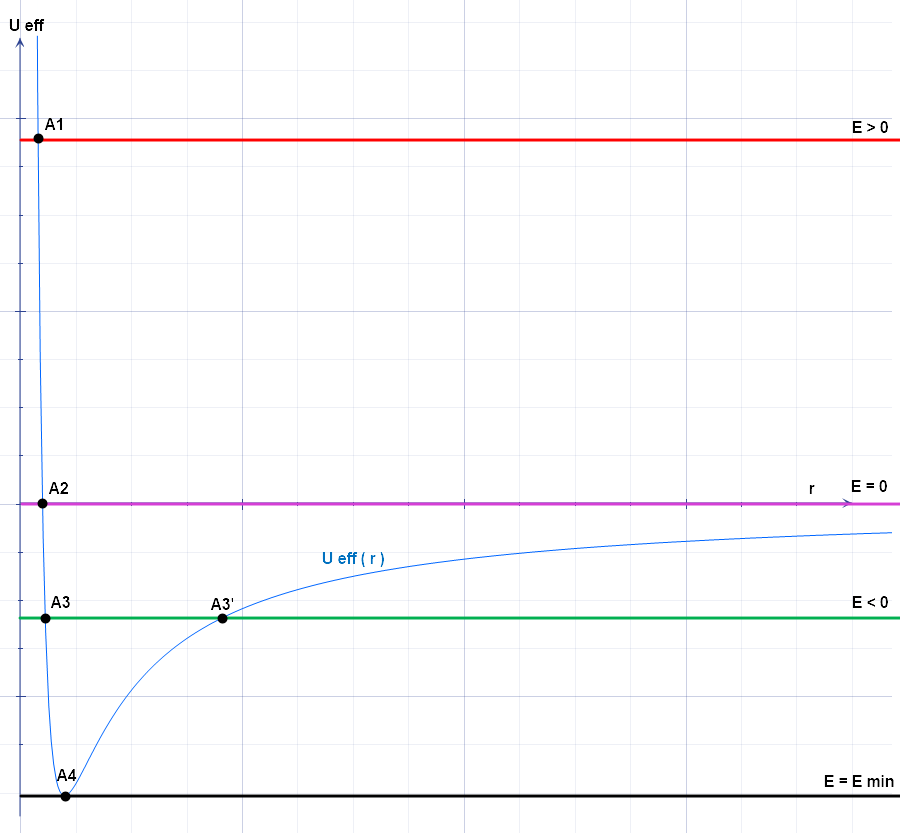
is the effective potential.A similar derivation may be found in José & Saletan, ''Classical Dynamics: A Contemporary Approach'', pp. 31–33. The original two-variable problem has been reduced to a one-variable problem. For many applications the effective potential can be treated exactly like the potential energy of a one-dimensional system: for instance, an energy diagram using the effective potential determines turning points and locations of stable and unstable equilibria. A similar method may be used in other applications, for instance, determining orbits in a general relativistic Schwarzschild metric.

Effective potentials are widely used in various condensed matter subfields, e.g. the Gauss-core potential (Likos 2002, Baeurle 2004) and the screened Coulomb potential (Likos 2001).

See also

* Geopotential

Notes

References

Further reading

* .
*
*
*

{{DEFAULTSORT:Effective Potential
Mechanics
Potentials