distributive lattice on:
[Wikipedia]
[Google]
[Amazon]
In
 Distributive lattices are ubiquitous but also rather specific structures. As already mentioned the main example for distributive lattices are lattices of sets, where join and meet are given by the usual set-theoretic operations. Further examples include:
* The Lindenbaum algebra of most
Distributive lattices are ubiquitous but also rather specific structures. As already mentioned the main example for distributive lattices are lattices of sets, where join and meet are given by the usual set-theoretic operations. Further examples include:
* The Lindenbaum algebra of most
Hasse diagrams of the two prototypical non-distributive lattices" align="center">
Image:M3 1xyz0.svg, The diamond lattice ''M''3 is non-distributive: = ''x'' ∧ 1 = ''x'' ≠ 0 = 0 ∨ 0 = .
Image:N5 1xyz0.svg, The pentagon lattice ''N''5 is non-distributive: = ''x'' ∧ 1 = ''x'' ≠ ''z'' = 0 ∨ ''z'' = .
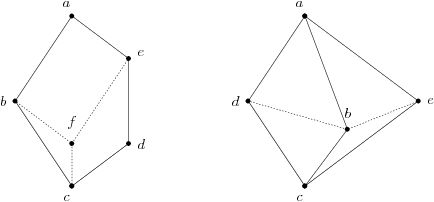 The simplest ''non-distributive'' lattices are ''M''3, the "diamond lattice", and ''N''5, the "pentagon lattice". A lattice is distributive if and only if none of its sublattices is isomorphic to ''M''3 or ''N''5; a sublattice is a subset that is closed under the meet and join operations of the original lattice. Note that this is not the same as being a subset that is a lattice under the original order (but possibly with different join and meet operations). Further characterizations derive from the representation theory in the next section.
An alternative way of stating the same fact is that every distributive lattice is a
The simplest ''non-distributive'' lattices are ''M''3, the "diamond lattice", and ''N''5, the "pentagon lattice". A lattice is distributive if and only if none of its sublattices is isomorphic to ''M''3 or ''N''5; a sublattice is a subset that is closed under the meet and join operations of the original lattice. Note that this is not the same as being a subset that is a lattice under the original order (but possibly with different join and meet operations). Further characterizations derive from the representation theory in the next section.
An alternative way of stating the same fact is that every distributive lattice is a
 The free distributive lattice over a set of generators ''G'' can be constructed much more easily than a general free lattice. The first observation is that, using the laws of distributivity, every term formed by the binary operations and on a set of generators can be transformed into the following equivalent ''normal form'':
:
where are finite meets of elements of ''G''. Moreover, since both meet and join are
The free distributive lattice over a set of generators ''G'' can be constructed much more easily than a general free lattice. The first observation is that, using the laws of distributivity, every term formed by the binary operations and on a set of generators can be transformed into the following equivalent ''normal form'':
:
where are finite meets of elements of ''G''. Moreover, since both meet and join are
mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, a distributive lattice is a lattice in which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection
In mathematics, the intersection of two or more objects is another object consisting of everything that is contained in all of the objects simultaneously. For example, in Euclidean geometry, when two lines in a plane are not parallel, thei ...
. Indeed, these lattices of sets describe the scenery completely: every distributive lattice is—up to isomorphism
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word i ...
—given as such a lattice of sets.
Definition
As in the case of arbitrary lattices, one can choose to consider a distributive lattice ''L'' either as a structure oforder theory
Order theory is a branch of mathematics that investigates the intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article intr ...
or of universal algebra
Universal algebra (sometimes called general algebra) is the field of mathematics that studies algebraic structures themselves, not examples ("models") of algebraic structures.
For instance, rather than take particular groups as the object of study ...
. Both views and their mutual correspondence are discussed in the article on lattices. In the present situation, the algebraic description appears to be more convenient.
A lattice (''L'',∨,∧) is distributive if the following additional identity holds for all ''x'', ''y'', and ''z'' in ''L'':
: ''x'' ∧ (''y'' ∨ ''z'') = (''x'' ∧ ''y'') ∨ (''x'' ∧ ''z'').
Viewing lattices as partially ordered sets, this says that the meet operation preserves
Fruit preserves are preparations of fruits whose main preserving agent is sugar and sometimes acid, often stored in glass jars and used as a condiment or spread.
There are many varieties of fruit preserves globally, distinguished by the met ...
non-empty finite joins. It is a basic fact of lattice theory that the above condition is equivalent to its dual:
: ''x'' ∨ (''y'' ∧ ''z'') = (''x'' ∨ ''y'') ∧ (''x'' ∨ ''z'') for all ''x'', ''y'', and ''z'' in ''L''.
In every lattice, defining ''p''≤''q'' as usual to mean ''p''∧''q''=''p'', the inequality ''x'' ∧ (''y'' ∨ ''z'') ≥ (''x'' ∧ ''y'') ∨ (''x'' ∧ ''z'') holds as well as its dual inequality ''x'' ∨ (''y'' ∧ ''z'') ≤ (''x'' ∨ ''y'') ∧ (''x'' ∨ ''z''). A lattice is distributive if one of the converse inequalities holds, too.
More information on the relationship of this condition to other distributivity conditions of order theory can be found in the article on distributivity (order theory)
In the mathematical area of order theory, there are various notions of the common concept of distributivity, applied to the formation of suprema and infima. Most of these apply to partially ordered sets that are at least lattices, but the concep ...
.
Morphisms
A morphism of distributive lattices is just a lattice homomorphism as given in the article on lattices, i.e. a function that is compatible with the two lattice operations. Because such a morphism of lattices preserves the lattice structure, it will consequently also preserve the distributivity (and thus be a morphism of distributive lattices).Examples
logic
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the science of deductively valid inferences or of logical truths. It is a formal science investigating how conclusions follow from prem ...
s that support conjunction
Conjunction may refer to:
* Conjunction (grammar), a part of speech
* Logical conjunction, a mathematical operator
** Conjunction introduction, a rule of inference of propositional logic
* Conjunction (astronomy), in which two astronomical bodies ...
and disjunction
In logic, disjunction is a logical connective typically notated as \lor and read aloud as "or". For instance, the English language sentence "it is raining or it is snowing" can be represented in logic using the disjunctive formula R \lor ...
is a distributive lattice, i.e. "and" distributes over "or" and vice versa.
* Every Boolean algebra
In mathematics and mathematical logic, Boolean algebra is a branch of algebra. It differs from elementary algebra in two ways. First, the values of the variables are the truth values ''true'' and ''false'', usually denoted 1 and 0, whereas i ...
is a distributive lattice.
* Every Heyting algebra In mathematics, a Heyting algebra (also known as pseudo-Boolean algebra) is a bounded lattice (with join and meet operations written ∨ and ∧ and with least element 0 and greatest element 1) equipped with a binary operation ''a'' → ''b'' of '' ...
is a distributive lattice. Especially this includes all locales and hence all open set
In mathematics, open sets are a generalization of open intervals in the real line.
In a metric space (a set along with a distance defined between any two points), open sets are the sets that, with every point , contain all points that are su ...
lattices of topological space
In mathematics, a topological space is, roughly speaking, a geometrical space in which closeness is defined but cannot necessarily be measured by a numeric distance. More specifically, a topological space is a set whose elements are called poin ...
s. Also note that Heyting algebras can be viewed as Lindenbaum algebras of intuitionistic logic
Intuitionistic logic, sometimes more generally called constructive logic, refers to systems of symbolic logic that differ from the systems used for classical logic by more closely mirroring the notion of constructive proof. In particular, systems ...
, which makes them a special case of the first example.
* Every totally ordered set
In mathematics, a total or linear order is a partial order in which any two elements are comparable. That is, a total order is a binary relation \leq on some set X, which satisfies the following for all a, b and c in X:
# a \leq a ( reflexive) ...
is a distributive lattice with max as join and min as meet.
* The natural number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country").
Numbers used for counting are called '' cardinal ...
s form a (conditionally complete) distributive lattice by taking the greatest common divisor
In mathematics, the greatest common divisor (GCD) of two or more integers, which are not all zero, is the largest positive integer that divides each of the integers. For two integers ''x'', ''y'', the greatest common divisor of ''x'' and ''y'' is ...
as meet and the least common multiple
In arithmetic and number theory, the least common multiple, lowest common multiple, or smallest common multiple of two integers ''a'' and ''b'', usually denoted by lcm(''a'', ''b''), is the smallest positive integer that is divisible by ...
as join. This lattice also has a least element, namely 1, which therefore serves as the identity element for joins.
* Given a positive integer ''n'', the set of all positive divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer m that may be multiplied by some integer to produce n. In this case, one also says that n is a multiple of m. An integer n is divisible or evenly divisible by ...
s of ''n'' forms a distributive lattice, again with the greatest common divisor as meet and the least common multiple as join. This is a Boolean algebra if and only if
In logic and related fields such as mathematics and philosophy, "if and only if" (shortened as "iff") is a biconditional logical connective between statements, where either both statements are true or both are false.
The connective is bic ...
''n'' is square-free.
* A lattice-ordered vector space is a distributive lattice.
* Young's lattice given by the inclusion ordering of Young diagrams representing integer partitions is a distributive lattice.
* The points of a distributive polytope (a convex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the n-dimensional Euclidean space \mathbb^n. Most texts. use the term "polytope" for a bounded convex polytope, and the w ...
closed under coordinatewise minimum and coordinatewise maximum operations), with these two operations as the join and meet operations of the lattice.
Early in the development of the lattice theory Charles S. Peirce
Charles Sanders Peirce ( ; September 10, 1839 – April 19, 1914) was an American philosopher, logician, mathematician and scientist who is sometimes known as "the father of pragmatism".
Educated as a chemist and employed as a scientist for t ...
believed that all lattices are distributive, that is, distributivity follows from the rest of the lattice axioms., p. xlvii.
However, independence proofs
Proof most often refers to:
* Proof (truth), argument or sufficient evidence for the truth of a proposition
* Alcohol proof, a measure of an alcoholic drink's strength
Proof may also refer to:
Mathematics and formal logic
* Formal proof, a co ...
were given by Schröder, Voigt,( de) Lüroth, Korselt, and Dedekind.
Characteristic properties
Various equivalent formulations to the above definition exist. For example, ''L'' is distributiveif and only if
In logic and related fields such as mathematics and philosophy, "if and only if" (shortened as "iff") is a biconditional logical connective between statements, where either both statements are true or both are false.
The connective is bic ...
the following holds for all elements ''x'', ''y'', ''z'' in ''L'':
: (''x''''y'')(''y''''z'')(''z''''x'') = (''x''''y'')(''y''''z'')(''z''''x'').
Similarly, ''L'' is distributive if and only if
: ''x''''z'' = ''y''''z'' and ''x''''z'' = ''y''''z'' always imply ''x''=''y''.
 The simplest ''non-distributive'' lattices are ''M''3, the "diamond lattice", and ''N''5, the "pentagon lattice". A lattice is distributive if and only if none of its sublattices is isomorphic to ''M''3 or ''N''5; a sublattice is a subset that is closed under the meet and join operations of the original lattice. Note that this is not the same as being a subset that is a lattice under the original order (but possibly with different join and meet operations). Further characterizations derive from the representation theory in the next section.
An alternative way of stating the same fact is that every distributive lattice is a
The simplest ''non-distributive'' lattices are ''M''3, the "diamond lattice", and ''N''5, the "pentagon lattice". A lattice is distributive if and only if none of its sublattices is isomorphic to ''M''3 or ''N''5; a sublattice is a subset that is closed under the meet and join operations of the original lattice. Note that this is not the same as being a subset that is a lattice under the original order (but possibly with different join and meet operations). Further characterizations derive from the representation theory in the next section.
An alternative way of stating the same fact is that every distributive lattice is a subdirect product In mathematics, especially in the areas of abstract algebra known as universal algebra, group theory, ring theory, and module theory, a subdirect product is a subalgebra of a direct product that depends fully on all its factors without however ne ...
of copies of the two-element chain, or that the only subdirectly irreducible member of the class of distributive lattices is the two-element chain. As a corollary, every Boolean lattice
In abstract algebra, a Boolean algebra or Boolean lattice is a complemented distributive lattice. This type of algebraic structure captures essential properties of both set operations and logic operations. A Boolean algebra can be seen as a ge ...
has this property as well.
Finally distributivity entails several other pleasant properties. For example, an element of a distributive lattice is meet-prime if and only if it is meet-irreducible, though the latter is in general a weaker property. By duality, the same is true for join-prime
A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every pair of elements has a unique supremum (also called a least upper bo ...
and join-irreducible elements. If a lattice is distributive, its covering relation forms a median graph..
Furthermore, every distributive lattice is also modular
Broadly speaking, modularity is the degree to which a system's components may be separated and recombined, often with the benefit of flexibility and variety in use. The concept of modularity is used primarily to reduce complexity by breaking a s ...
.
Representation theory
The introduction already hinted at the most important characterization for distributive lattices: a lattice is distributive if and only if it is isomorphic to a lattice of sets (closed underset union
In set theory, the union (denoted by ∪) of a collection of sets is the set of all elements in the collection. It is one of the fundamental operations through which sets can be combined and related to each other.
A refers to a union of ze ...
and intersection
In mathematics, the intersection of two or more objects is another object consisting of everything that is contained in all of the objects simultaneously. For example, in Euclidean geometry, when two lines in a plane are not parallel, thei ...
). (The latter structure is sometimes called a ring of sets
In mathematics, there are two different notions of a ring of sets, both referring to certain Family of sets, families of sets.
In order theory, a nonempty family of sets \mathcal is called a ring (of sets) if it is closure (mathematics), closed u ...
in this context.) That set union and intersection are indeed distributive in the above sense is an elementary fact. The other direction is less trivial, in that it requires the representation theorems stated below. The important insight from this characterization is that the identities (equations) that hold in all distributive lattices are exactly the ones that hold in all lattices of sets in the above sense.
Birkhoff's representation theorem
:''This is about lattice theory. For other similarly named results, see Birkhoff's theorem (disambiguation).''
In mathematics, Birkhoff's representation theorem for distributive lattices states that the elements of any finite distributive lattic ...
for distributive lattices states that every ''finite'' distributive lattice is isomorphic to the lattice of lower set
In mathematics, an upper set (also called an upward closed set, an upset, or an isotone set in ''X'') of a partially ordered set (X, \leq) is a subset S \subseteq X with the following property: if ''s'' is in ''S'' and if ''x'' in ''X'' is larger ...
s of the poset
In mathematics, especially order theory, a partially ordered set (also poset) formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary r ...
of its join-prime (equivalently: join-irreducible) elements. This establishes a bijection
In mathematics, a bijection, also known as a bijective function, one-to-one correspondence, or invertible function, is a function between the elements of two sets, where each element of one set is paired with exactly one element of the other ...
(up to isomorphism
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word i ...
) between the class of all finite posets and the class of all finite distributive lattices. This bijection can be extended to a duality of categories between homomorphisms of finite distributive lattices and monotone function
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order ...
s of finite posets. Generalizing this result to infinite lattices, however, requires adding further structure.
Another early representation theorem is now known as Stone's representation theorem for distributive lattices (the name honors Marshall Harvey Stone, who first proved it). It characterizes distributive lattices as the lattices of compact
Compact as used in politics may refer broadly to a pact or treaty; in more specific cases it may refer to:
* Interstate compact
* Blood compact, an ancient ritual of the Philippines
* Compact government, a type of colonial rule utilized in Britis ...
open
Open or OPEN may refer to:
Music
* Open (band), Australian pop/rock band
* The Open (band), English indie rock band
* Open (Blues Image album), ''Open'' (Blues Image album), 1969
* Open (Gotthard album), ''Open'' (Gotthard album), 1999
* Open (C ...
sets of certain topological space
In mathematics, a topological space is, roughly speaking, a geometrical space in which closeness is defined but cannot necessarily be measured by a numeric distance. More specifically, a topological space is a set whose elements are called poin ...
s. This result can be viewed both as a generalization of Stone's famous representation theorem for Boolean algebras and as a specialization of the general setting of Stone duality
In mathematics, there is an ample supply of categorical dualities between certain categories of topological spaces and categories of partially ordered sets. Today, these dualities are usually collected under the label Stone duality, since they f ...
.
A further important representation was established by Hilary Priestley in her representation theorem for distributive lattices. In this formulation, a distributive lattice is used to construct a topological space with an additional partial order on its points, yielding a (completely order-separated) ''ordered Stone space'' (or '' Priestley space''). The original lattice is recovered as the collection of clopen
In topology, a clopen set (a portmanteau of closed-open set) in a topological space is a set which is both open and closed. That this is possible may seem counter-intuitive, as the common meanings of and are antonyms, but their mathematical de ...
lower sets of this space.
As a consequence of Stone's and Priestley's theorems, one easily sees that any distributive lattice is really isomorphic to a lattice of sets. However, the proofs of both statements require the Boolean prime ideal theorem
In mathematics, the Boolean prime ideal theorem states that ideals in a Boolean algebra can be extended to prime ideals. A variation of this statement for filters on sets is known as the ultrafilter lemma. Other theorems are obtained by cons ...
, a weak form of the axiom of choice
In mathematics, the axiom of choice, or AC, is an axiom of set theory equivalent to the statement that ''a Cartesian product of a collection of non-empty sets is non-empty''. Informally put, the axiom of choice says that given any collection ...
.
Free distributive lattices
associative
In mathematics, the associative property is a property of some binary operations, which means that rearranging the parentheses in an expression will not change the result. In propositional logic, associativity is a valid rule of replacement ...
, commutative
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Most familiar as the name of ...
and idempotent
Idempotence (, ) is the property of certain operations in mathematics and computer science whereby they can be applied multiple times without changing the result beyond the initial application. The concept of idempotence arises in a number of pl ...
, one can ignore duplicates and order, and represent a join of meets like the one above as a set of sets:
:
where the are finite subsets of ''G''. However, it is still possible that two such terms denote the same element of the distributive lattice. This occurs when there are indices ''j'' and ''k'' such that is a subset of In this case the meet of will be below the meet of and hence one can safely remove the ''redundant'' set without changing the interpretation of the whole term. Consequently, a set of finite subsets of ''G'' will be called ''irredundant'' whenever all of its elements are mutually incomparable (with respect to the subset ordering); that is, when it forms an antichain of finite sets.
Now the free distributive lattice over a set of generators ''G'' is defined on the set of all finite irredundant sets of finite subsets of ''G''. The join of two finite irredundant sets is obtained from their union by removing all redundant sets. Likewise the meet of two sets ''S'' and ''T'' is the irredundant version of The verification that this structure is a distributive lattice with the required universal property
In mathematics, more specifically in category theory, a universal property is a property that characterizes up to an isomorphism the result of some constructions. Thus, universal properties can be used for defining some objects independently fr ...
is routine.
The number of elements in free distributive lattices with ''n'' generators is given by the Dedekind number
File:Monotone Boolean functions 0,1,2,3.svg, 400px, The free distributive lattices of monotonic Boolean functions on 0, 1, 2, and 3 arguments, with 2, 3, 6, and 20 elements respectively (move mouse over right diagram to see description)
circle 6 ...
s. These numbers grow rapidly, and are known only for ''n'' ≤ 8; they are
:2, 3, 6, 20, 168, 7581, 7828354, 2414682040998, 56130437228687557907788 .
The numbers above count the number of elements in free distributive lattices in which the lattice operations are joins and meets of finite sets of elements, including the empty set. If empty joins and empty meets are disallowed, the resulting free distributive lattices have two fewer elements; their numbers of elements form the sequence
:0, 1, 4, 18, 166, 7579, 7828352, 2414682040996, 56130437228687557907786 .
See also
*Completely distributive lattice In the mathematical area of order theory, a completely distributive lattice is a complete lattice in which arbitrary joins distribute over arbitrary meets.
Formally, a complete lattice ''L'' is said to be completely distributive if, for any doub ...
— a lattice in which infinite joins distribute over infinite meets
* Duality theory for distributive lattices In mathematics, duality theory for distributive lattices provides three different (but closely related) representations of bounded distributive lattices via Priestley spaces, spectral spaces, and pairwise Stone spaces. This duality, which is ori ...
* Spectral space In mathematics, a spectral space is a topological space that is homeomorphic to the spectrum of a commutative ring. It is sometimes also called a coherent space because of the connection to coherent topos.
Definition
Let ''X'' be a topological ...
References
Further reading
* * {{Order theory Lattice theory