Diffraction formalism on:
[Wikipedia]
[Google]
[Amazon]
Diffraction processes affecting 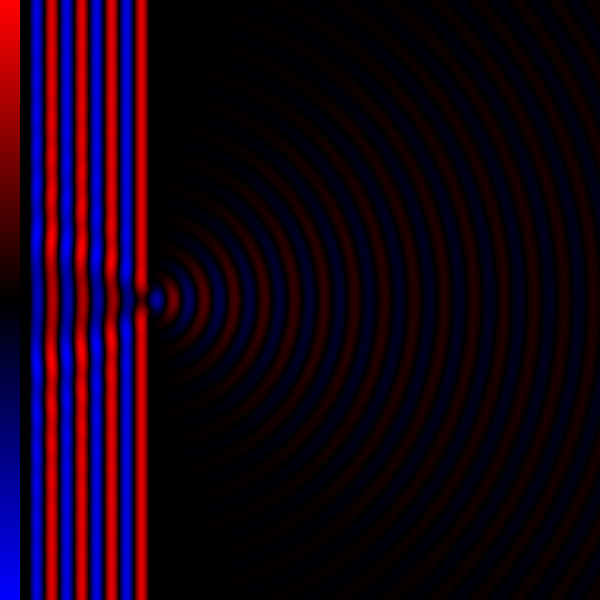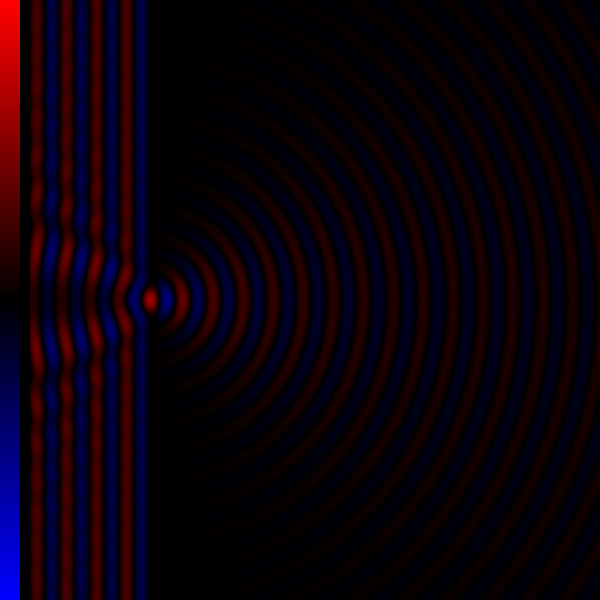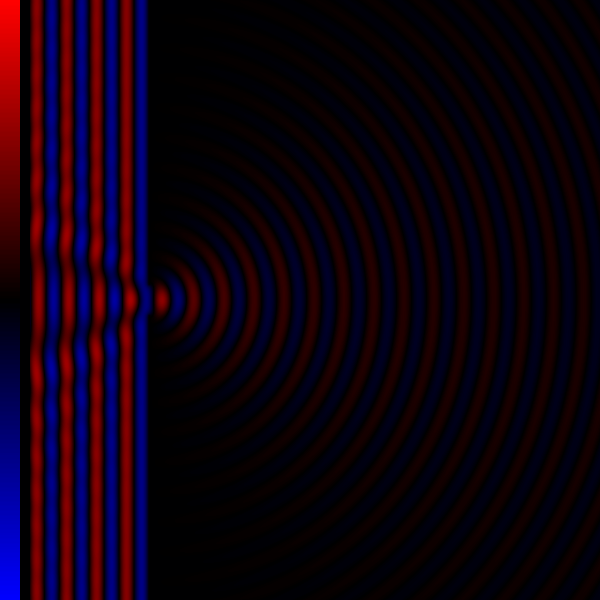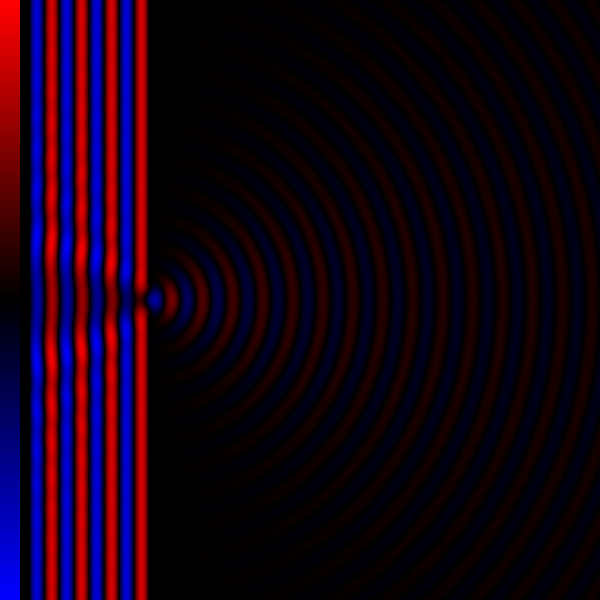

 As an example, an exact equation can now be derived for the intensity of the diffraction pattern as a function of angle in the case of single-slit diffraction.
A mathematical representation of Huygens' principle can be used to start an equation.
Consider a monochromatic complex plane wave of wavelength ''λ'' incident on a slit of width ''a''.
If the slit lies in the x′-y′ plane, with its center at the origin, then it can be assumed that diffraction generates a complex wave ψ, traveling radially in the r direction away from the slit, and this is given by:
Let be a point inside the slit over which it is being integrated. If is the location at which the intensity of the diffraction pattern is being computed, the slit extends from to , and from to .
The distance ''r'' from the slot is:
Assuming
As an example, an exact equation can now be derived for the intensity of the diffraction pattern as a function of angle in the case of single-slit diffraction.
A mathematical representation of Huygens' principle can be used to start an equation.
Consider a monochromatic complex plane wave of wavelength ''λ'' incident on a slit of width ''a''.
If the slit lies in the x′-y′ plane, with its center at the origin, then it can be assumed that diffraction generates a complex wave ψ, traveling radially in the r direction away from the slit, and this is given by:
Let be a point inside the slit over which it is being integrated. If is the location at which the intensity of the diffraction pattern is being computed, the slit extends from to , and from to .
The distance ''r'' from the slot is:
Assuming
wave
In physics, mathematics, and related fields, a wave is a propagating dynamic disturbance (change from equilibrium) of one or more quantities. Waves can be periodic, in which case those quantities oscillate repeatedly about an equilibrium (re ...
s are amenable to quantitative
Quantitative may refer to:
* Quantitative research, scientific investigation of quantitative properties
* Quantitative analysis (disambiguation)
* Quantitative verse, a metrical system in poetry
* Statistics, also known as quantitative analysis ...
description and analysis. Such treatments are applied to a wave passing through one or more slits whose width is specified as a proportion of the wavelength
In physics, the wavelength is the spatial period of a periodic wave—the distance over which the wave's shape repeats.
It is the distance between consecutive corresponding points of the same phase on the wave, such as two adjacent crests, t ...
. Numerical approximation
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods th ...
s may be used, including the Fresnel
Augustin-Jean Fresnel (10 May 1788 – 14 July 1827) was a French civil engineer and physicist whose research in optics led to the almost unanimous acceptance of the wave theory of light, excluding any remnant of Newton's corpuscular the ...
and Fraunhofer approximations.


General diffraction
Because diffraction is the result of addition of all waves (of given wavelength) along all unobstructed paths, the usual procedure is to consider the contribution of an infinitesimally small neighborhood around a certain path (this contribution is usually called awavelet
A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a "brief oscillation". A taxonomy of wavelets has been established, based on the num ...
) and then integrate over all paths (= add all wavelets) from the source to the detector (or given point on a screen).
Thus in order to determine the pattern produced by diffraction, the phase and the amplitude of each of the wavelets is calculated. That is, at each point in space we must determine the distance to each of the simple sources on the incoming wavefront. If the distance to each of the simple sources differs by an integer number of wavelengths, all the wavelets will be in phase, resulting in constructive interference. If the distance to each source is an integer plus one half of a wavelength, there will be complete destructive interference. Usually, it is sufficient to determine these minima and maxima to explain the observed diffraction effects.
The simplest descriptions of diffraction are those in which the situation can be reduced to a two-dimensional problem. For water waves, this is already the case, as water waves propagate only on the surface of the water. For light, we can often neglect one dimension if the diffracting object extends in that direction over a distance far greater than the wavelength. In the case of light shining through small circular holes we will have to take into account the full three-dimensional nature of the problem.
Several qualitative observations can be made of diffraction in general:
* The angular spacing of the features in the diffraction pattern is inversely proportional to the dimensions of the object causing the diffraction. In other words: the smaller the diffracting object, the wider the resulting diffraction pattern, and vice versa. (More precisely, this is true of the sines of the angles.)
* The diffraction angles are invariant under scaling; that is, they depend only on the ratio of the wavelength to the size of the diffracting object.
* When the diffracting object has a periodic structure, for example in a diffraction grating, the features generally become sharper. The fourth figure, for example, shows a comparison of a double-slit pattern with a pattern formed by five slits, both sets of slits having the same spacing between the center of one slit and the next.
Approximations
The problem of calculating what a diffracted wave looks like, is the problem of determining the phase of each of the simple sources on the incoming wave front. It is mathematically easier to consider the case of far-field orFraunhofer diffraction
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when plane waves are incident on a diffracting object, and the diffraction pattern is viewed at a sufficiently long distance (a distance satisfying Fraunhofer ...
, where the point of observation is far from that of the diffracting obstruction, and as a result, involves less complex mathematics than the more general case of near-field or Fresnel diffraction
In optics, the Fresnel diffraction equation for near-field diffraction is an approximation of the Kirchhoff–Fresnel diffraction that can be applied to the propagation of waves in the near field. It is used to calculate the diffraction pattern ...
. To make this statement more quantitative, consider a diffracting object at the origin that has a size . For definiteness let us say we are diffracting light and we are interested in what the intensity looks like on a screen a distance away from the object. At some point on the screen the path length to one side of the object is given by the Pythagorean theorem
:
If we now consider the situation where , the path length becomes
This is the Fresnel approximation. To further simplify things: If the diffracting object is much smaller than the distance , the last term will contribute much less than a wavelength to the path length, and will then not change the phase appreciably. That is . The result is the Fraunhofer approximation, which is only valid very far away from the object
Depending on the size of the diffraction object, the distance to the object and the wavelength of the wave, the Fresnel approximation, the Fraunhofer approximation or neither approximation may be valid. As the distance between the measured point of diffraction and the obstruction point increases, the diffraction patterns or results predicted converge towards those of Fraunhofer diffraction, which is more often observed in nature due to the extremely small wavelength of visible light.
Multiple narrow slits
A simple quantitative description
Multiple-slit arrangements can be mathematically considered as multiple simple wave sources, if the slits are narrow enough. For light, a slit is an opening that is infinitely extended in one dimension, and this has the effect of reducing a wave problem in 3D-space to a simpler problem in 2D-space. The simplest case is that of two narrow slits, spaced a distance apart. To determine the maxima and minima in the amplitude we must determine the path difference to the first slit and to the second one. In the Fraunhofer approximation, with the observer far away from the slits, the difference in path length to the two slits can be seen from the image to be Maxima in the intensity occur if this path length difference is an integer number of wavelengths. where * is aninteger
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the languag ...
that labels the ''order'' of each maximum,
* is the wavelength,
* is the distance between the slits, and
* is the angle at which constructive interference occurs.
The corresponding minima are at path differences of an integer number plus one half of the wavelength:
For an array of slits, positions of the minima and maxima are not changed, the ''fringes'' visible on a screen however do become sharper, as can be seen in the image.
Mathematical description
To calculate this intensity pattern, one needs to introduce some more sophisticated methods. The mathematical representation of a radial wave is given by where , is the wavelength, is frequency of the wave and is the phase of the wave at the slits at time ''t'' = 0. The wave at a screen some distance away from the plane of the slits is given by the sum of the waves emanating from each of the slits. To make this problem a little easier, we introduce the complex wave , the real part of which is equal to The absolute value of this function gives the wave amplitude, and the complex phase of the function corresponds to the phase of the wave. is referred to as the complex amplitude. With slits, the total wave at point on the screen is Since we are for the moment only interested in the amplitude and relative phase, we can ignore any overall phase factors that are not dependent on or . We approximate . In the Fraunhofer limit we can neglect terms of order in the exponential, and any terms involving or in the denominator. The sum becomes The sum has the form of ageometric sum
In mathematics, a geometric series is the sum of an infinite number of terms that have a constant ratio between successive terms. For example, the series
:\frac \,+\, \frac \,+\, \frac \,+\, \frac \,+\, \cdots
is geometric, because each succ ...
and can be evaluated to give
The intensity is given by the absolute value of the complex amplitude squared
where denotes the complex conjugate
In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, (if a and b are real, then) the complex conjugate of a + bi is equal to a - ...
of .
Single slit
 As an example, an exact equation can now be derived for the intensity of the diffraction pattern as a function of angle in the case of single-slit diffraction.
A mathematical representation of Huygens' principle can be used to start an equation.
Consider a monochromatic complex plane wave of wavelength ''λ'' incident on a slit of width ''a''.
If the slit lies in the x′-y′ plane, with its center at the origin, then it can be assumed that diffraction generates a complex wave ψ, traveling radially in the r direction away from the slit, and this is given by:
Let be a point inside the slit over which it is being integrated. If is the location at which the intensity of the diffraction pattern is being computed, the slit extends from to , and from to .
The distance ''r'' from the slot is:
Assuming
As an example, an exact equation can now be derived for the intensity of the diffraction pattern as a function of angle in the case of single-slit diffraction.
A mathematical representation of Huygens' principle can be used to start an equation.
Consider a monochromatic complex plane wave of wavelength ''λ'' incident on a slit of width ''a''.
If the slit lies in the x′-y′ plane, with its center at the origin, then it can be assumed that diffraction generates a complex wave ψ, traveling radially in the r direction away from the slit, and this is given by:
Let be a point inside the slit over which it is being integrated. If is the location at which the intensity of the diffraction pattern is being computed, the slit extends from to , and from to .
The distance ''r'' from the slot is:
Assuming Fraunhofer diffraction
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when plane waves are incident on a diffracting object, and the diffraction pattern is viewed at a sufficiently long distance (a distance satisfying Fraunhofer ...
will result in the conclusion . In other words, the distance to the target is much larger than the diffraction width on the target.
By the binomial expansion
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial into a sum involving terms of the form , where the ...
rule, ignoring terms quadratic and higher, the quantity on the right can be estimated to be:
It can be seen that 1/''r'' in front of the equation is non-oscillatory, i.e. its contribution to the magnitude of the intensity is small compared to our exponential factors. Therefore, we will lose little accuracy by approximating it as 1/''z''.
To make things cleaner, a placeholder ''C'' is used to denote constants in the equation. It is important to keep in mind that ''C'' can contain imaginary numbers, thus the wave function will be complex. However, at the end, the ''ψ'' will be bracketed, which will eliminate any imaginary components.
Now, in Fraunhofer diffraction, is small, so (note that participates in this exponential and it is being integrated).
In contrast the term can be eliminated from the equation, since when bracketed it gives 1.
(For the same reason we have also eliminated the term )
Taking results in:
It can be noted through Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that fo ...
and its derivatives that and .