Domain coloring

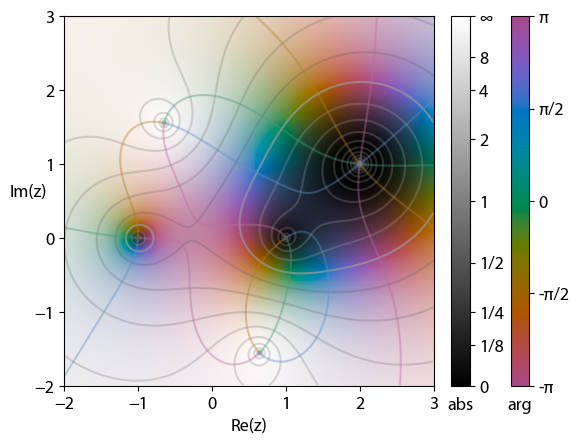
In complex analysis, domain coloring or a color wheel graph is a technique for visualizing complex functions by assigning a color to each point of the complex plane. By assigning points on the complex plane to different colors and brightness, domain coloring allows for a function from the complex plane to itself, whose graph would normally require four spatial dimensions, to be easily represented and understood. This provides insight to the fluidity of complex functions and shows natural geometric extensions of real functions.

Motivation

A graph of a real function can be drawn in two dimensions because there are two represented variables, $x$ and $y$. However, complex numbers are represented by two variables and therefore two dimensions; this means that representing a complex function (more precisely, a complex-valued function of one complex variable $f: \mathbb \to \mathbb$) requires the visualization of four dimensions. One way to achieve that is with a Riemann surface, but another method is by domain coloring.

History

The term "domain coloring" was coined by Frank Farris, possibly around 1998. Lundmark refers to Farris' coining the term "domain coloring" in this 2004 article. There were many earlier uses of color to visualize complex functions, typically mapping argument ( phase) to hue.
Larry Crone used the method in the late 1980s.
Dan Kucerovsky used it in 1990. The technique of using continuous color to map points from domain to codomain or image plane was used in 1999 by George Abdo and Paul Godfrey and colored grids were used in graphics by Doug Arnold that he dates to 1997.

Method

Representing a four dimensional complex mapping with only two variables is undesirable, as methods like projections can result in a loss of information. However, it is possible to add variables that keep the four-dimensional process without requiring a visualization of four dimensions. In this case, the two added variables are visual inputs such as color and brightness because they are naturally two variables easily processed and distinguished by the human eye. This assignment is called a "color function". There are many different color functions used. A common practice is to represent the complex argument, $\arg z$, (also known as "phase" or "angle") with a hue following the color wheel, and the magnitude by other means, such as brightness or saturation.

Simple color function

The following example colors the origin in black, in green, in magenta, and a point at infinity in white:
$\begin H & = \arg z + 2\pi / 3,\\ S & = 100\%,\\ L & = \ell(, z, ). \end$
Where H is hue, S is saturation, and L is lightness.
There are a number of choices for the function \ell: strictly monotonic and Continuous function">continuous.
Another desirable property is $\ell(1/r) = 1 - \ell(r)$ such that
the inverse of a function is exactly as light as the original function is dark (and the other way around). Possible choices include
* $\ell_1(r) = \frac \arctan(r)$ and
* $\ell_2(r) = \frac$ (with some parameter $a>0$). With $a=2$, this corresponds to the stereographic projection onto the Riemann sphere.

A widespread choice which does not have this property is the function $\ell_3(r) = 1 - a^$ (with some parameter $0 < a < 1$) which for $a=1/2$ and $0\le r \le 1$ is very close to $\ell_1$.

This approach uses the HSL (hue, saturation, lightness) color model. Saturation is always set at the maximum of 100%. Vivid colors of the rainbow are rotating in a continuous way on the complex unit circle, so the sixth roots of unity (starting with 1) are: green, cyan, blue, magenta, red, and yellow.

Since the HSL color space is not perceptually uniform, one can see streaks of perceived brightness at yellow, cyan, and magenta (even though their absolute values are the same as red, green, and blue) and a halo around . More modern color spaces, e.g, the Lab color space or CIECAM02, correct this, making the images more accurate and less saturated.

Discontinuous color changing

Many color graphs have discontinuities, where instead of evenly changing brightness and color, it suddenly changes, even when the function itself is still smooth. This is done for a variety of reasons such as showing more detail or highlighting certain aspects of a function, like level sets.

Magnitude growth

Unlike the argument, which has finite range, the magnitude of a complex number can range from to . Therefore, in functions that have large ranges of magnitude, changes in magnitude can sometimes be hard to differentiate when a very large change is also pictured in the graph. This can be remedied with a discontinuous color function which shows a repeating brightness pattern for the magnitude based on a given equation. This allows smaller changes to be easily seen as well as larger changes that "discontinuously jump" to a higher magnitude. In the graph on the right, these discontinuities occur in circles around the center, and show a dimming of the graph that can then start becoming brighter again. A similar color function has been used for the graph on top of the article.

Equations that determine the discontinuities may be linear, such as for every integer magnitude, exponential equations such as every magnitude $2^n$ where ''n'' is an integer, or any other equation.

Highlighting properties

Discontinuities may be placed where outputs have a certain property to highlight which parts of the graph have that property. For instance, a graph may, instead of showing the color cyan, jump from green to blue. This causes a discontinuity that is easy to spot, and can highlight lines such as where the argument is zero. Discontinuities may also affect large portions of a graph, such as a graph where the color wheel divides the graph into quadrants. In this way, it is easy to show where each quadrant ends up with relations to others.

Limitations

People who experience color blindness may have trouble interpreting such graphs when they are made with standard color maps. This issue can be partially fixed by creating alternate versions using color maps that fit within the color space discernible to those with color blindness. For example, for use by those with total deuteranopia, a color map based on blue/grey/yellow may be more readable than the conventional map based on blue/green/red.

References

External links

Samuel Li's function plotter

High-quality, browser-based interactive complex function plotter by Ricky Reusseur



Complex Mapper
by Alessandro Rosa
John Davis software
S-Lang script for domain coloring
Open source C and Python domain coloring softwareEnhanced 3D Domain coloringDomain Coloring Method on GPUJava domain coloring software (In development)
*MATLAB routine


Python script for GIMP by Michael J. Gruber
*Matplotlib and MayaVi implementation of domain coloring by E. Petriso

* MATLABbr>routines with user interface and various color schemes
* MATLABbr>routines for 3D-visualization of complex functions

Color wheel method

Real-Time Zooming Math Engine

Fractal Zoomer : Software that utilizes domain coloring

cplot, a domain-coloring package for Python

{{DEFAULTSORT:Domain Coloring
Complex analysis
Numerical function drawing