Delta-sigma Modulation on:
[Wikipedia]
[Google]
[Amazon]
 Delta-sigma (ΔΣ; or sigma-delta, ΣΔ) modulation is an oversampling method for encoding signals into low bit depth digital signals at a very high sample-frequency as part of the process of delta-sigma analog-to-digital converters (ADCs) and digital-to-analog converters (DACs). Delta-sigma modulation achieves high
Delta-sigma (ΔΣ; or sigma-delta, ΣΔ) modulation is an oversampling method for encoding signals into low bit depth digital signals at a very high sample-frequency as part of the process of delta-sigma analog-to-digital converters (ADCs) and digital-to-analog converters (DACs). Delta-sigma modulation achieves high
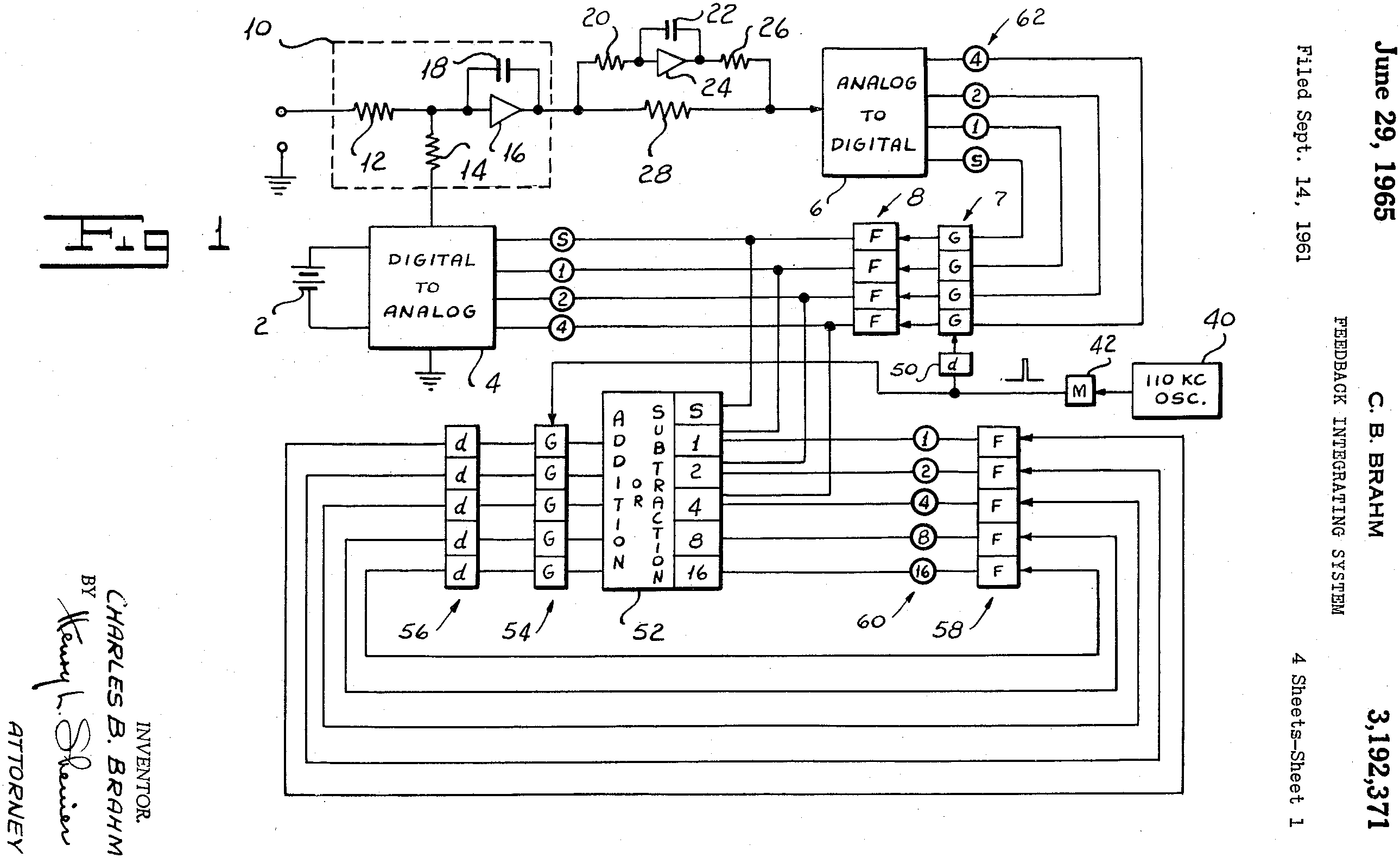 The principle of improving the resolution of a coarse quantizer by use of feedback, which is the basic principle of delta-sigma conversion, was first described in a 1954-filed patent by C. Chapin Cutler of
The principle of improving the resolution of a coarse quantizer by use of feedback, which is the basic principle of delta-sigma conversion, was first described in a 1954-filed patent by C. Chapin Cutler of
 Noise of the quantizer can be further shaped by replacing the quantizer itself with another ΔΣ modulator. This creates a 2-order modulator, which can be rearranged in a cascaded fashion (Figure 2). This process can be repeated to increase the order even more.
While 1-order modulators are unconditionally stable, stability analysis must be performed for higher-order noise-feedback modulators. Alternatively, noise-feedforward configurations are always stable and have simpler analysis.
Noise of the quantizer can be further shaped by replacing the quantizer itself with another ΔΣ modulator. This creates a 2-order modulator, which can be rearranged in a cascaded fashion (Figure 2). This process can be repeated to increase the order even more.
While 1-order modulators are unconditionally stable, stability analysis must be performed for higher-order noise-feedback modulators. Alternatively, noise-feedforward configurations are always stable and have simpler analysis.
by Jwin-Yen Guo and Teng-Hung Chang Higher bit quantizers inherently produce less quantization noise. One criticism of 1-bit quantization is that adequate amounts of
 When a signal is quantized, the resulting signal can be approximated by addition of white noise with approximately equal intensity across the entire spectrum. In reality, the quantization noise is, of course, not independent of the signal and this dependence results in limit cycles and is the source of idle tones and pattern noise in delta-sigma converters. However, adding dithering noise (Figure 3) reduces such
When a signal is quantized, the resulting signal can be approximated by addition of white noise with approximately equal intensity across the entire spectrum. In reality, the quantization noise is, of course, not independent of the signal and this dependence results in limit cycles and is the source of idle tones and pattern noise in delta-sigma converters. However, adding dithering noise (Figure 3) reduces such
 As illustrated in Figure 4, the total amount of quantization noise is the same both in a Nyquist converter (yellow + green areas) and in an oversampling converter (blue + green areas). But oversampling converters distribute that noise over a much wider frequency range. The benefit is that the total amount of noise in the frequency band of interest is dramatically smaller for oversampling converters (just the small green area), than for a Nyquist converter (yellow + green total area).
As illustrated in Figure 4, the total amount of quantization noise is the same both in a Nyquist converter (yellow + green areas) and in an oversampling converter (blue + green areas). But oversampling converters distribute that noise over a much wider frequency range. The benefit is that the total amount of noise in the frequency band of interest is dramatically smaller for oversampling converters (just the small green area), than for a Nyquist converter (yellow + green total area).
 The Laplace transform of integration of a function of time corresponds to simply multiplication by in Laplace notation. The integrator is assumed to be an ideal integrator to keep the math simple, but a real integrator (or similar filter) may have a more complicated expression.
The process of quantization is approximated as addition with a quantization error noise source. The noise is often assumed to be white and independent of the signal, though as explains that is not always a valid assumption (particularly for low-bit quantization).
Since the system and Laplace transform are linear, the total behavior of this system can be analyzed by separating how it affects the input from how it affects the noise:
The Laplace transform of integration of a function of time corresponds to simply multiplication by in Laplace notation. The integrator is assumed to be an ideal integrator to keep the math simple, but a real integrator (or similar filter) may have a more complicated expression.
The process of quantization is approximated as addition with a quantization error noise source. The noise is often assumed to be white and independent of the signal, though as explains that is not always a valid assumption (particularly for low-bit quantization).
Since the system and Laplace transform are linear, the total behavior of this system can be analyzed by separating how it affects the input from how it affects the noise:
 Integration in discrete-time can be an accumulator which repeatedly sums its input
Integration in discrete-time can be an accumulator which repeatedly sums its input
quality
Quality may refer to:
Concepts
*Quality (business), the ''non-inferiority'' or ''superiority'' of something
*Quality (philosophy), an attribute or a property
*Quality (physics), in response theory
*Energy quality, used in various science discipli ...
by utilizing a negative feedback
Negative feedback (or balancing feedback) occurs when some function (Mathematics), function of the output of a system, process, or mechanism is feedback, fed back in a manner that tends to reduce the fluctuations in the output, whether caused ...
loop during quantization to the lower bit depth that continuously corrects quantization errors and moves quantization noise to higher frequencies well above the original signal's bandwidth. Subsequent low-pass filtering for demodulation easily removes this high frequency noise and time averages to achieve high accuracy in amplitude, which can be ultimately encoded as pulse-code modulation (PCM).
Both ADCs and DACs can employ delta-sigma modulation. A delta-sigma ADC (e.g. Figure 1 top) encodes an analog signal using high-frequency delta-sigma modulation and then applies a digital filter
In signal processing, a digital filter is a system that performs mathematical operations on a Sampling (signal processing), sampled, discrete-time signal to reduce or enhance certain aspects of that signal. This is in contrast to the other ma ...
to demodulate it to a high-bit digital output at a lower sampling-frequency. A delta-sigma DAC (e.g. Figure 1 bottom) encodes a high-resolution digital input signal into a lower-resolution but higher sample-frequency signal that may then be mapped to voltage
Voltage, also known as (electrical) potential difference, electric pressure, or electric tension, is the difference in electric potential between two points. In a Electrostatics, static electric field, it corresponds to the Work (electrical), ...
s and smoothed with an analog filter for demodulation. In both cases, the temporary use of a low bit depth signal at a higher sampling frequency simplifies circuit design and takes advantage of the efficiency and high accuracy in time of digital electronics
Digital electronics is a field of electronics involving the study of digital signals and the engineering of devices that use or produce them. It deals with the relationship between Binary number, binary inputs and outputs by passing electrical s ...
.
Primarily because of its cost efficiency and reduced circuit complexity, this technique has found increasing use in modern electronic components such as DACs, ADCs, frequency synthesizers, switched-mode power supplies and motor controllers. The coarsely-quantized output of a delta-sigma ADC is occasionally used directly in signal processing or as a representation for signal storage (e.g., Super Audio CD
Super Audio CD (SACD) is an optical disc format for audio storage introduced in 1999. It was developed jointly by Sony and Philips Electronics and intended to be the successor to the compact disc (CD) format.
The SACD format allows multiple a ...
stores the raw output of a 1-bit delta-sigma modulator).
While this article focuses on synchronous modulation, which requires a precise clock for quantization, asynchronous delta-sigma modulation instead runs without a clock.
Motivation
When transmitting an analog signal directly, allnoise
Noise is sound, chiefly unwanted, unintentional, or harmful sound considered unpleasant, loud, or disruptive to mental or hearing faculties. From a physics standpoint, there is no distinction between noise and desired sound, as both are vibrat ...
in the system and transmission is added to the analog signal, reducing its quality. Digitizing
Digitization is the process of converting information into a digital (i.e. computer-readable) format.Collins Dictionary. (n.d.). Definition of 'digitize'. Retrieved December 15, 2021, from https://www.collinsdictionary.com/dictionary/english ...
it enables noise-free transmission, storage, and processing. There are many methods of digitization.
In Nyquist-rate ADCs, an analog signal is sampled at a relatively low sampling frequency just above its Nyquist rate (twice the signal's highest frequency) and quantized by a multi-level quantizer to produce a multi-bit digital signal
A digital signal is a signal that represents data as a sequence of discrete values; at any given time it can only take on, at most, one of a finite number of values. This contrasts with an analog signal, which represents continuous values; ...
. Such higher-bit methods seek accuracy in amplitude directly, but require extremely precise components and so may suffer from poor linearity.
Advantages of oversampling
Oversampling converters instead produce a lower bit depth result at a much higher sampling frequency. This can achieve comparable quality by taking advantage of: * Higher accuracy in time (afforded by high-speed digital circuits and highly accurate clocks). * Higher linearity afforded by low-bit ADCs and DACs (for instance, a 1-bit DAC that only outputs two values of a precise high voltage and a precise low voltage is perfectly linear, in principle). *Noise shaping
Noise shaping is a technique typically used in digital audio, Image processing, image, and video processing, usually in combination with dithering, as part of the process of Quantization (signal processing), quantization or Audio bit depth, bit-dep ...
: moving noise to higher frequencies above the signal of interest, so they can be easily removed with low-pass filtering.
* Reduced steepness requirement for the analog low-pass anti-aliasing filters. High-order filters with a flat passband cost more to make in the analog domain than in the digital domain.
Frequency/resolution tradeoff
Another key aspect given by oversampling is the frequency/resolution tradeoff. The decimation filter put after the modulator not only filters the whole sampled signal in the band of interest (cutting the noise at higher frequencies), but also reduces the sampling rate, and hence the representable frequency range, of the signal, while increasing the sample amplitude resolution. This improvement in amplitude resolution is obtained by a sort of ''averaging'' of the higher-data-rate bitstream.Improvement over delta modulation
Delta modulation is an earlier related low-bit oversampling method that also usesnegative feedback
Negative feedback (or balancing feedback) occurs when some function (Mathematics), function of the output of a system, process, or mechanism is feedback, fed back in a manner that tends to reduce the fluctuations in the output, whether caused ...
, but only encodes the derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is t ...
of the signal (its ''delta'') rather than its amplitude. The result is a stream of marks and spaces representing up or down of the signal's movement, which must be integrated to reconstruct the signal's amplitude. Delta modulation has several drawbacks. The differentiation alters the signal's spectrum by amplifying high-frequency noise, attenuating low-frequencies, and dropping the DC component. This makes its dynamic range and signal-to-noise ratio
Signal-to-noise ratio (SNR or S/N) is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. SNR is defined as the ratio of signal power to noise power, often expressed in deci ...
(SNR) inversely proportional to signal frequency. Delta modulation suffers from slope overload if signals move too fast. And it is susceptible to transmission disturbances that result in cumulative error.
Delta-sigma modulation rearranges the integrator and quantizer of a delta modulator so that the output carries information corresponding to the amplitude of the input signal instead of just its derivative. This also has the benefit of incorporating desirable noise shaping into the conversion process, to deliberately move quantization noise to frequencies higher than the signal. Since the accumulated error signal is lowpass filtered by the delta-sigma modulator's integrator before being quantized, the subsequent negative feedback of its quantized result effectively subtracts the low-frequency components of the quantization noise while leaving the higher frequency components of the noise.
1-bit delta-sigma modulation is pulse-density modulation
In the specific case of a single-bit synchronous ΔΣ ADC, an analog voltage signal is effectively converted into a pulse frequency, or pulse density, which can be understood as pulse-density modulation (PDM). A sequence of positive and negative pulses, representing bits at a known fixed rate, is very easy to generate, transmit, and accurately regenerate at the receiver, given only that the timing and sign of the pulses can be recovered. Given such a sequence of pulses from a delta-sigma modulator, the original waveform can be reconstructed with adequate precision. The use of PDM as a signal representation is an alternative to PCM. Alternatively, the high-frequency PDM can later be downsampled through decimation and requantized to convert it into a multi-bit PCM code at a lower sampling frequency closer to the Nyquist rate of the frequency band of interest.History and variations
The seminal paper combining feedback with oversampling to achieve delta modulation was by F. de Jager of Philips Research Laboratories in 1952. The principle of improving the resolution of a coarse quantizer by use of feedback, which is the basic principle of delta-sigma conversion, was first described in a 1954-filed patent by C. Chapin Cutler of
The principle of improving the resolution of a coarse quantizer by use of feedback, which is the basic principle of delta-sigma conversion, was first described in a 1954-filed patent by C. Chapin Cutler of Bell Labs
Nokia Bell Labs, commonly referred to as ''Bell Labs'', is an American industrial research and development company owned by Finnish technology company Nokia. With headquarters located in Murray Hill, New Jersey, Murray Hill, New Jersey, the compa ...
. It was not named as such until a 1962 paper by Inose et al. of University of Tokyo, which came up with the idea of adding a filter in the forward path of the delta modulator. However, Charles B Brahm of United Aircraft Corp in 1961 filed a patent "Feedback integrating system" with a feedback loop containing an integrator with multi-bit quantization shown in its Fig 1.
Wooley's "The Evolution of Oversampling Analog-to-Digital Converters" gives more history and references to relevant patents. Some avenues of variation (which may be applied in different combinations) are the modulator's order, the quantizer's bit depth, the manner of decimation, and the oversampling ratio.
Higher-order modulator
Multi-bit quantizer
The modulator can also be classified by the bit depth of its quantizer. A quantizer that distinguishes between ''N-levels'' is called a ''log2N'' bit quantizer. For example, a simple comparator has 2 levels and so is 1 bit quantizer; a 3-level quantizer is called a ''1.5'' bit quantizer; a 4-level quantizer is a 2-bit quantizer; a 5-level quantizer is called a ''2.5-bit'' quantizer.Sigma-delta class-D amplifier and control method for a sigma-delta class-D amplifierby Jwin-Yen Guo and Teng-Hung Chang Higher bit quantizers inherently produce less quantization noise. One criticism of 1-bit quantization is that adequate amounts of
dither
Dither is an intentionally applied form of noise used to randomize quantization error, preventing large-scale patterns such as color banding in images. Dither is routinely used in processing of both digital audio and video data, and is ofte ...
cannot be used in the feedback loop, so distortion can be heard under some conditions (more discussion at ).
Subsequent decimation
Decimation is strongly associated with delta-sigma modulation, but is distinct and outside the scope of this article. The original 1962 paper didn't describe decimation. Oversampled data in the early days was sent as is. The proposal to decimate oversampled delta-sigma data usingdigital filter
In signal processing, a digital filter is a system that performs mathematical operations on a Sampling (signal processing), sampled, discrete-time signal to reduce or enhance certain aspects of that signal. This is in contrast to the other ma ...
ing before converting it into PCM audio was made by D. J. Goodman at Bell Labs in 1969, to reduce the ΔΣ signal from its high sampling rate while increasing its bit depth. Decimation may be done in a separate chip on the receiving end of the delta-sigma bit stream, sometimes by a dedicated module inside of a microcontroller
A microcontroller (MC, uC, or μC) or microcontroller unit (MCU) is a small computer on a single integrated circuit. A microcontroller contains one or more CPUs (processor cores) along with memory and programmable input/output peripherals. Pro ...
, which is useful for interfacing with PDM MEMS microphones, though many ΔΣ ADC integrated circuits include decimation. Some microcontrollers even incorporate both the modulator and decimator.
Decimation filters most commonly used for ΔΣ ADCs, in order of increasing complexity and quality, are:
# Boxcar moving average filter ( simple moving average or sinc-in-frequency or sinc filter): This is the easiest digital filter and retains a sharp step response, but is mediocre at separating frequency bands and suffers from intermodulation distortion. The filter can be implemented by simply counting how many samples during a larger sampling interval are high. The 1974 paper from another Bell Labs researcher, J. C. Candy, "A Use of Limit Cycle Oscillations to Obtain Robust Analog-to-Digital Converters" was one of the early examples of this.
# Cascaded integrator–comb filters: These are called sinc filters, equivalent to cascading the above sinc filter N times and rearranging the order of operations for computational efficiency. Lower N filters are simpler, settle faster, and have less attenuation in the baseband, while higher N filters are slightly more complex and settle slower and have more droop in the passband, but better attenuate undesired high frequency noise. Compensation filters can however be applied to counteract undesired passband attenuation. Sinc filters are appropriate for decimating sigma delta modulation down to four times the Nyquist rate. The height of the first sideload is -13·N dB and the height of successive lobes fall off gradually, but only the areas around the nulls will alias into the low frequency band of interest; for instance when downsampling by 8, the largest ''aliased'' high frequency component may be -16 dB below the peak of the band of interest with a sinc filter but -40 dB below for a sinc filter, and if only interested in a narrower bandwidth, even fewer high frequency components will alias into it (see Figures 7–9 of Lyons article).
# Windowed sinc-in-time (brick-wall in frequency) filters: Although the sinc function's infinite support prevents it from being realizable in finite time, the sinc function can instead be windowed to realize finite impulse response filters. This approximated filter design, while maintaining ''almost no'' attenuation of the lower-frequency band of interest, still removes ''almost all'' undesired high-frequency noise. The downside is poor performance in the time domain (e.g. step response overshoot and ripple), higher delay (i.e. their convolution
In mathematics (in particular, functional analysis), convolution is a operation (mathematics), mathematical operation on two function (mathematics), functions f and g that produces a third function f*g, as the integral of the product of the two ...
time is inversely proportional to their cutoff transition steepness), and higher computational requirements. They are the de facto standard for high fidelity
High fidelity (hi-fi or, rarely, HiFi) is the high-quality reproduction of sound. It is popular with audiophiles and home audio enthusiasts. Ideally, high-fidelity equipment has inaudible noise and distortion, and a flat (neutral, uncolored) ...
digital audio converters.
Other loop filters
Most commercial ΔΣ modulators use integrators as the loop filter, because as low-pass filters they push quantization noise up in frequency, which is useful for baseband signals. But a ΔΣ modulator's filter does not necessarily need to be a low-pass filter. If a band-pass filter is used instead, then quantization noise is moved up and down in frequency away from the filter's pass-band, so a subsequent pass-band decimation filter will result in a ΔΣ ADC with a bandpass characteristic.Reduction of baseband noise by increasing oversampling ratio and ΔΣM order
 When a signal is quantized, the resulting signal can be approximated by addition of white noise with approximately equal intensity across the entire spectrum. In reality, the quantization noise is, of course, not independent of the signal and this dependence results in limit cycles and is the source of idle tones and pattern noise in delta-sigma converters. However, adding dithering noise (Figure 3) reduces such
When a signal is quantized, the resulting signal can be approximated by addition of white noise with approximately equal intensity across the entire spectrum. In reality, the quantization noise is, of course, not independent of the signal and this dependence results in limit cycles and is the source of idle tones and pattern noise in delta-sigma converters. However, adding dithering noise (Figure 3) reduces such distortion
In signal processing, distortion is the alteration of the original shape (or other characteristic) of a signal. In communications and electronics it means the alteration of the waveform of an information-bearing signal, such as an audio signal ...
by making quantization noise more random.
ΔΣ ADCs reduce the amount of this noise in the baseband by spreading it out and shaping it so it is mostly in higher frequencies. It can then be easily filtered out with inexpensive digital filters, without high-precision analog circuits needed by Nyquist ADCs.
Oversampling to spread out quantization noise
Quantization noise in the baseband frequency range (from DC to ) may be reduced by increasing the oversampling ratio (OSR) defined by : where is the sampling frequency and is the Nyquist rate (the minimum sampling rate needed to avoid aliasing, which is twice the original signal's maximum frequency ). Since oversampling is typically done in powers of two, represents how many times OSR is doubled.Noise shaping
Figure 4 shows how ΔΣ modulation shapes noise to further reduce the amount of quantization noise in the baseband in exchange for increasing noise at higher frequencies (where it can be easily filtered out). The curves of higher-order ΔΣ modulators achieve even greater reduction of noise in the baseband. These curves are derived using mathematical tools called theLaplace transform
In mathematics, the Laplace transform, named after Pierre-Simon Laplace (), is an integral transform that converts a Function (mathematics), function of a Real number, real Variable (mathematics), variable (usually t, in the ''time domain'') to a f ...
(for continuous-time signals, e.g. in an ADC's modulation loop) or the Z-transform (for discrete-time signals, e.g. in a DAC's modulation loop). These transforms are useful for converting harder math from the time domain into simpler math in the complex frequency domain of the complex variable (in the Laplace domain) or (in the z-domain).
Analysis of ΔΣ ADC modulation loop in Laplace domain
Figure 5 represents the 1-order ΔΣ ADC modulation loop (from Figure 1) as a continuous-time linear time-invariant system in the Laplace domain with the equation:= Low-pass filter on input
= To understand how the system affect the input signal only, the noise is temporarily imagined to be 0: which can be rearranged to yield the followingtransfer function
In engineering, a transfer function (also known as system function or network function) of a system, sub-system, or component is a function (mathematics), mathematical function that mathematical model, models the system's output for each possible ...
:
This transfer function has a single pole at in the complex plane, so it effectively acts as a 1-order low-pass filter on the input signal. (Note: its cutoff frequency could be adjusted as desired by including multiplication by a constant in the loop).
= High-pass filter on noise
= To understand how the system affects the noise only, the input instead is temporarily imagined to be 0: which can be rearranged to yield the following transfer function: This transfer function has a single zero at and a single pole at so the system effectively acts as a high-pass filter on the noise that starts at 0 at DC, then gradually rises until it reaches the cutoff frequency, and then levels off.Analysis of synchronous ΔΣ modulation loop in z-domain
The synchronous ΔΣ DAC's modulation loop (Figure 6) meanwhile is in discrete-time and so its analysis is in the z-domain. It is very similar to the above analysis in Laplace domain and produces similar curves. Note: many sources also analyze a ΔΣ ADC's modulation loop in the z-domain, which implicitly treats the continuous analog input as a discrete-time signal. This may be a valid approximation provided that the input signal is already bandlimited and can be assumed to be not changing on time scales higher than the sampling rate. It is particularly appropriate when the modulator is implemented as a switched capacitor circuit, which work by transferring charge between capacitors in clocked time steps.