Complex Polytope

In geometry, a complex polytope is a generalization of a polytope in real space to an analogous structure in a complex Hilbert space, where each real dimension is accompanied by an imaginary one.

A complex polytope may be understood as a collection of complex points, lines, planes, and so on, where every point is the junction of multiple lines, every line of multiple planes, and so on.

Precise definitions exist only for the regular complex polytopes, which are configurations. The regular complex polytopes have been completely characterized, and can be described using a symbolic notation developed by Coxeter.

Some complex polytopes which are not fully regular have also been described.

Definitions and introduction

The complex line $\mathbb^1$ has one dimension with real coordinates and another with imaginary coordinates. Applying real coordinates to both dimensions is said to give it two dimensions over the real numbers. A real plane, with the imaginary axis labelled as such, is called an Argand diagram. Because of this it is sometimes called the complex plane. Complex 2-space (also sometimes called the complex plane) is thus a four-dimensional space over the reals, and so on in higher dimensions.

A complex ''n''-polytope in complex ''n''-space is the analogue of a real ''n''- polytope in real ''n''-space.

There is no natural complex analogue of the ordering of points on a real line (or of the associated combinatorial properties). Because of this a complex polytope cannot be seen as a contiguous surface and it does not bound an interior in the way that a real polytope does.

In the case of ''regular'' polytopes, a precise definition can be made by using the notion of symmetry. For any regular polytope the symmetry group (here a complex reflection group, called a Shephard group) acts transitively on the flags, that is, on the nested sequences of a point contained in a line contained in a plane and so on.

More fully, say that a collection ''P'' of affine subspaces (or ''flats'') of a complex unitary space ''V'' of dimension ''n'' is a regular complex polytope if it meets the following conditions:
* for every , if is a flat in ''P'' of dimension ''i'' and is a flat in ''P'' of dimension ''k'' such that then there are at least two flats ''G'' in ''P'' of dimension ''j'' such that ;
* for every such that , if are flats of ''P'' of dimensions ''i'', ''j'', then the set of flats between ''F'' and ''G'' is connected, in the sense that one can get from any member of this set to any other by a sequence of containments; and
* the subset of unitary transformations of ''V'' that fix ''P'' are transitive on the ''flags'' of flats of ''P'' (with of dimension ''i'' for all ''i'').

(Here, a flat of dimension −1 is taken to mean the empty set.) Thus, by definition, regular complex polytopes are configurations in complex unitary space.

The regular complex polytopes were discovered by Shephard (1952), and the theory was further developed by Coxeter (1974).

A complex polytope exists in the complex space of equivalent dimension. For example, the vertices of a complex polygon are points in the complex plane $\mathbb^2$, and the edges are complex lines $\mathbb^1$ existing as (affine) subspaces of the plane and intersecting at the vertices. Thus, an edge can be given a coordinate system consisting of a single complex number.

In a regular complex polytope the vertices incident on the edge are arranged symmetrically about their centroid, which is often used as the origin of the edge's coordinate system (in the real case the centroid is just the midpoint of the edge). The symmetry arises from a complex reflection about the centroid; this reflection will leave the magnitude of any vertex unchanged, but change its argument by a fixed amount, moving it to the coordinates of the next vertex in order. So we may assume (after a suitable choice of scale) that the vertices on the edge satisfy the equation $x^p - 1 = 0$ where ''p'' is the number of incident vertices. Thus, in the Argand diagram of the edge, the vertex points lie at the vertices of a regular polygon centered on the origin.

Three real projections of regular complex polygon 42 are illustrated above, with edges ''a, b, c, d, e, f, g, h''. It has 16 vertices, which for clarity have not been individually marked. Each edge has four vertices and each vertex lies on two edges, hence each edge meets four other edges. In the first diagram, each edge is represented by a square. The sides of the square are ''not'' parts of the polygon but are drawn purely to help visually relate the four vertices. The edges are laid out symmetrically. (Note that the diagram looks similar to the B₄ Coxeter plane projection of the tesseract, but it is structurally different).

The middle diagram abandons octagonal symmetry in favour of clarity. Each edge is shown as a real line, and each meeting point of two lines is a vertex. The connectivity between the various edges is clear to see.

The last diagram gives a flavour of the structure projected into three dimensions: the two cubes of vertices are in fact the same size but are seen in perspective at different distances away in the fourth dimension.

Regular complex one-dimensional polytopes

A real 1-dimensional polytope exists as a closed segment in the real line $\mathbb^1$, defined by its two end points or vertices in the line. Its Schläfli symbol is .

Analogously, a complex 1-polytope exists as a set of ''p'' vertex points in the complex line $\mathbb^1$. These may be represented as a set of points in an Argand diagram (''x'',''y'')=''x''+''iy''. A regular complex 1-dimensional polytope _''p'' has ''p'' (''p'' ≥ 2) vertex points arranged to form a convex regular polygon in the Argand plane.

Unlike points on the real line, points on the complex line have no natural ordering. Thus, unlike real polytopes, no interior can be defined. Despite this, complex 1-polytopes are often drawn, as here, as a bounded regular polygon in the Argand plane.

A regular real 1-dimensional polytope is represented by an empty Schläfli symbol , or Coxeter-Dynkin diagram . The dot or node of the Coxeter-Dynkin diagram itself represents a reflection generator while the circle around the node means the generator point is not on the reflection, so its reflective image is a distinct point from itself. By extension, a regular complex 1-dimensional polytope in $\mathbb^1$ has Coxeter-Dynkin diagram , for any positive integer ''p'', 2 or greater, containing ''p'' vertices. ''p'' can be suppressed if it is 2. It can also be represented by an empty Schläfli symbol _''p'', }_''p'' {, or ₁{2}₁.)

The symmetry is denoted by the Coxeter diagram , and can alternatively be described in Coxeter notation as _''p''[], []_''p'' or ]_''p''[, _''p'' sub>1 or _''p''[1]_''p''. The symmetry is isomorphic to the cyclic group, order ''p''. The subgroups of _''p''[] are any whole divisor ''d'', _''d''[], where ''d''≥2.

A unitary operator generator for is seen as a rotation by 2π/''p'' radians counter clockwise, and a edge is created by sequential applications of a single unitary reflection. A unitary reflection generator for a 1-polytope with ''p'' vertices is . When ''p'' = 2, the generator is ''e''^π''i'' = –1, the same as a point reflection in the real plane.

In higher complex polytopes, 1-polytopes form ''p''-edges. A 2-edge is similar to an ordinary real edge, in that it contains two vertices, but need not exist on a real line.

Regular complex polygons

While 1-polytopes can have unlimited ''p'', finite regular complex polygons, excluding the double prism polygons _''p''{4}₂, are limited to 5-edge (pentagonal edges) elements, and infinite regular apeirogons also include 6-edge (hexagonal edges) elements.

Notations

Shephard's modified Schläfli notation

Shephard originally devised a modified form of Schläfli's notation for regular polytopes. For a polygon bounded by ''p''₁-edges, with a ''p''₂-set as vertex figure and overall symmetry group of order ''g'', we denote the polygon as ''p''₁(''g'')''p''₂.

The number of vertices ''V'' is then ''g''/''p''₂ and the number of edges ''E'' is ''g''/''p''₁.

The complex polygon illustrated above has eight square edges (''p''₁=4) and sixteen vertices (''p''₂=2). From this we can work out that ''g'' = 32, giving the modified Schläfli symbol 4(32)2.

Coxeter's revised modified Schläfli notation

A more modern notation _''p''1{''q''}_''p''2 is due to Coxeter, and is based on group theory. As a symmetry group, its symbol is _''p''1 'q''sub>''p''₂.

The symmetry group _''p''1 'q''sub>''p''₂ is represented by 2 generators R₁, R₂, where: R₁^''p''₁ = R₂^''p''₂ = I. If ''q'' is even, (R₂R₁)^''q''/2 = (R₁R₂)^''q''/2. If ''q'' is odd, (R₂R₁)^(q−1)/2R₂ = (R₁R₂)^{(''q''−1)/2}R₁. When ''q'' is odd, ''p''₁=''p''₂.

For ₄ sub>2 has R₁⁴ = R₂² = I, (R₂R₁)² = (R₁R₂)².

For ₃ sub>3 has R₁³ = R₂³ = I, (R₂R₁)²R₂ = (R₁R₂)²R₁.

Coxeter-Dynkin diagrams

Coxeter also generalised the use of Coxeter-Dynkin diagrams to complex polytopes, for example the complex polygon _''p''{''q''}_''r'' is represented by and the equivalent symmetry group, _''p'' 'q''sub>''r'', is a ringless diagram . The nodes ''p'' and ''r'' represent mirrors producing ''p'' and ''r'' images in the plane. Unlabeled nodes in a diagram have implicit 2 labels. For example, a real regular polygon is ₂{''q''}₂ or {''q''} or .

One limitation, nodes connected by odd branch orders must have identical node orders. If they do not, the group will create "starry" polygons, with overlapping element. So and are ordinary, while is starry.

12 Irreducible Shephard groups

Coxeter enumerated this list of regular complex polygons in $\mathbb{C}^2$. A regular complex polygon, _''p''{''q''}_''r'' or , has ''p''-edges, and ''r''-gonal vertex figures. _''p''{''q''}_''r'' is a finite polytope if (''p''+''r'')''q''>''pr''(''q''-2).

Its symmetry is written as _''p'' 'q''sub>''r'', called a '' Shephard group'', analogous to a Coxeter group, while also allowing unitary reflections.

For nonstarry groups, the order of the group _''p'' 'q''sub>''r'' can be computed as $g = 8/q \cdot (1/p+2/q+1/r-1)^{-2}$.

The Coxeter number for _''p'' 'q''sub>''r'' is $h = 2/(1/p+2/q+1/r-1)$, so the group order can also be computed as $g = 2h^2/q$. A regular complex polygon can be drawn in orthogonal projection with ''h''-gonal symmetry.

The rank 2 solutions that generate complex polygons are:
{, class=wikitable
, - align=center
!rowspan=3, Group
, G₃=G(''q'',1,1) , , G₂=G(''p'',1,2), , G₄, , G₆, , G₅, , G₈, , G₁₄, , G₉, , G₁₀, , G₂₀, , G₁₆, , G₂₁, , G₁₇, , G₁₈
, - align=center
, ₂ 'q''sub>2, ''q''=3,4..., , _''p'' sub>2, ''p''=2,3..., , ₃ sub>3, , ₃ sub>2, , ₃ sub>3, , ₄ sub>4, , ₃ sub>2, , ₄ sub>2, , ₄ sub>3, , ₃ sub>3, , ₅ sub>5, , ₃ 0sub>2, , ₅ sub>2, , ₅ sub>3
, - align=center
, , , , , , , , , , , , , , , , , , , , , , , , , , ,
, - align=center
!Order
, 2''q'', , 2''p''², , 24, , 48, , 72, , 96, , 144, , 192, , 288, , 360, , 600, , 720, , 1200, , 1800
, - align=center
! h
, ''q'', , 2''p'', , 6, , colspan=3, 12, , colspan=3, 24, , colspan=2, 30, , colspan=3, 60

Excluded solutions with odd ''q'' and unequal ''p'' and ''r'' are: ₆ sub>2, ₆ sub>3, ₉ sub>3, ₁₂ sub>3, ..., ₅ sub>2, ₆ sub>2, ₈ sub>2, ₉ sub>2, ₄ sub>2, ₉ sub>2, ₃ sub>2, and ₃ 1sub>2.

Other whole ''q'' with unequal ''p'' and ''r'', create starry groups with overlapping fundamental domains: , , , , , and .

The dual polygon of _''p''{''q''}_''r'' is _''r''{''q''}_''p''. A polygon of the form _''p''{''q''}_''p'' is self-dual. Groups of the form _''p'' ''q''sub>2 have a half symmetry _''p'' 'q''sub>''p'', so a regular polygon is the same as quasiregular . As well, regular polygon with the same node orders, , have an alternated construction , allowing adjacent edges to be two different colors.

The group order, ''g'', is used to compute the total number of vertices and edges. It will have ''g''/''r'' vertices, and ''g''/''p'' edges. When ''p''=''r'', the number of vertices and edges are equal. This condition is required when ''q'' is odd.

Matrix generators

The group ''p'' 'q'''r'', , can be represented by two matrices:
{, class=wikitable
, +
!Name, , R₁
, , R₂

, - align=center
!Order
, ''p''
, ''r''
, -
!Matrix
,
\left begin{smallmatrix}
e^{2\pi i/p} & 0 \\
(e^{2\pi i/p}-1)k & 1 \\
\end{smallmatrix}\right
,
\left begin{smallmatrix}
1 & (e^{2\pi i/r}-1)k \\
0 & e^{2\pi i/r} \\
\end{smallmatrix}\right

With
: k=$\sqrt \frac{ cos(\frac{\pi}{p}-\frac{\pi}{r})+cos(\frac{2\pi}{q}) }{2\sin\frac{\pi}{p}\sin\frac{\pi}{r} }$

;Examples
{, class=wikitable
, - valign=top
,
{, class=wikitable
, +
!Name, , R₁
, , R₂

, - align=center
!Order
, ''p''
, ''q''
, -
!Matrix
,
\left begin{smallmatrix}
e^{2\pi i/p} & 0 \\
0 & 1 \\
\end{smallmatrix}\right
,
\left begin{smallmatrix}
1 & 0 \\
0 & e^{2\pi i/q} \\
\end{smallmatrix}\right

,
{, class=wikitable
, +
!Name, , R₁
, , R₂

, - align=center
!Order
, ''p''
, 2
, -
!Matrix
,
\left begin{smallmatrix}
e^{2\pi i/p} & 0 \\
0 & 1 \\
\end{smallmatrix}\right
,
\left begin{smallmatrix}
0 & 1 \\
1 & 0 \\
\end{smallmatrix}\right

,
{, class=wikitable
, +
!Name, , R₁
, , R₂

, - align=center
!Order
, 3
, 3
, -
!Matrix
,
\left begin{smallmatrix}
\frac{-1+\sqrt3 i}{2} & 0 \\
\frac{-3+\sqrt3 i}{2} & 1 \\
\end{smallmatrix}\right
,
\left begin{smallmatrix}
1 & \frac{-3+\sqrt3 i}{2} \\
0 & \frac{-1+\sqrt3 i}{2} \\
\end{smallmatrix}\right

, - valign=top
,
{, class=wikitable
, +
!Name, , R₁
, , R₂

, - align=center
!Order
, 4
, 4
, -
!Matrix
,
\left begin{smallmatrix}
i & 0 \\
0 & 1 \\
\end{smallmatrix}\right
,
\left begin{smallmatrix}
1 & 0 \\
0 & i \\
\end{smallmatrix}\right

,
{, class=wikitable
, +
!Name, , R₁
, , R₂

, - align=center
!Order
, 4
, 2
, -
!Matrix
,
\left begin{smallmatrix}
i & 0 \\
0 & 1 \\
\end{smallmatrix}\right
,
\left begin{smallmatrix}
0 & 1 \\
1 & 0 \\
\end{smallmatrix}\right

,
{, class=wikitable
, +
!Name, , R₁
, , R₂

, - align=center
!Order
, 3
, 2
, -
!Matrix
,
\left begin{smallmatrix}
\frac{-1+\sqrt3 i}{2} & 0 \\
\frac{-3+\sqrt3 i}{2} & 1 \\
\end{smallmatrix}\right
,
\left begin{smallmatrix}
1 & -2 \\
0 & -1 \\
\end{smallmatrix}\right

Enumeration of regular complex polygons

Coxeter enumerated the complex polygons in Table III of Regular Complex Polytopes.
{, class="wikitable sortable"
!Group, , data-sort-type="number", Order, , data-sort-type="number", Coxeter
number, , colspan=2, Polygon, , data-sort-type="number", Vertices, , colspan=2 data-sort-type="number", Edges, , Notes
, - align=center BGCOLOR="#ffe0e0"
, G(q,q,2)
₂ 'q''sub>2 = 'q''BR>q=2,3,4,..., , 2''q'', , ''q'' , , ₂{''q''}₂, , , , ''q'', , ''q'', , {} , , align=left, Real regular polygons
Same as
Same as if ''q'' even

{, class="wikitable sortable"
!Group, , data-sort-type="number", Order, , data-sort-type="number", Coxeter
number, , colspan=3, Polygon, , data-sort-type="number", Vertices, , colspan=2 data-sort-type="number", Edges, , Notes
, - align=center BGCOLOR="#ffffe0"
, rowspan=2, G(''p'',1,2)
_''p'' sub>2
p=2,3,4,... , , rowspan=2, 2''p''² , , rowspan=2, 2''p'' , , ''p''(2''p''²)2, , _''p''{4}₂, ,          
, , ''p''² , , 2''p'', , _''p''{} , , align=left, same as _''p''{}×_''p''{} or
$\mathbb{R}^4$ representation as ''p''-''p'' duoprism
, - align=center BGCOLOR="#ffffe0"
, 2(2''p''²)''p'', , ₂{4}_''p'' , , , , 2''p'' , , ''p''², , {} , , align=left, $\mathbb{R}^4$ representation as ''p''-''p'' duopyramid

, - align=center BGCOLOR="#ffe0e0"
, G(2,1,2)
₂ sub>2 = , , 8 , , 4 , , , , ₂{4}₂ = {4}, , , , 4 , , 4, , {} , , align=left, same as {}×{} or
Real square

, - align=center BGCOLOR="#e0ffff"
, rowspan=2, G(3,1,2)
₃ sub>2 , , rowspan=2, 18 , , rowspan=2, 6 , , 6(18)2, , ₃{4}₂, , , , 9 , , 6, , ₃{} , , align=left, same as ₃{}×₃{} or
$\mathbb{R}^4$ representation as 3-3 duoprism
, - align=center BGCOLOR="#e0ffff"
, 2(18)3, , ₂{4}₃ , , , , 6 , , 9, , {} , , align=left, $\mathbb{R}^4$ representation as 3-3 duopyramid

, - align=center BGCOLOR="#e0ffff"
, rowspan=2, G(4,1,2)
₄ sub>2 , , rowspan=2, 32 , , rowspan=2, 8 , , 8(32)2, , ₄{4}₂, , , , 16 , , 8, , ₄{} , , align=left, same as ₄{}×₄{} or
$\mathbb{R}^4$ representation as 4-4 duoprism or {4,3,3}
, - align=center BGCOLOR="#e0ffff"
, 2(32)4, , ₂{4}₄ , , , , 8 , , 16, , {} , , align=left, $\mathbb{R}^4$ representation as 4-4 duopyramid or {3,3,4}

, - align=center BGCOLOR="#e0ffff"
, rowspan=2, G(5,1,2)
₅ sub>2 , , rowspan=2, 50 , , rowspan=2, 25 , , 5(50)2, , ₅{4}₂, , , , 25 , , 10, , ₅{} , , align=left, same as ₅{}×₅{} or
$\mathbb{R}^4$ representation as 5-5 duoprism
, - align=center BGCOLOR="#e0ffff"
, 2(50)5, , ₂{4}₅ , , , , 10 , , 25, , {} , , align=left, $\mathbb{R}^4$ representation as 5-5 duopyramid

, - align=center BGCOLOR="#e0ffff"
, rowspan=2, G(6,1,2)
₆ sub>2 , , rowspan=2, 72 , , rowspan=2, 36 , , 6(72)2, , ₆{4}₂, , , , 36 , , 12, , ₆{} , , align=left, same as ₆{}×₆{} or
$\mathbb{R}^4$ representation as 6-6 duoprism
, - align=center BGCOLOR="#e0ffff"
, 2(72)6, , ₂{4}₆ , , , , 12 , , 36, , {} , , align=left, $\mathbb{R}^4$ representation as 6-6 duopyramid

, - align=center BGCOLOR="#e0f0ff"
, G₄=G(1,1,2)
₃ sub>3
<2,3,3> , , 24 , , 6 , , 3(24)3 , , ₃{3}₃, , , , 8 , , 8, , ₃{} , , align=left, Möbius–Kantor configuration
self-dual, same as
$\mathbb{R}^4$ representation as {3,3,4}
, - align=center BGCOLOR="#e0f0ff"
, rowspan=4, G_6
3 sub>2, , rowspan=4, 48 , , rowspan=4, 12 , , 3(48)2 , , ₃{6}₂, , , , rowspan=2, 24, , rowspan=2, 16, , rowspan=2, ₃{} , , align=left, same as
, - align=center BGCOLOR="#e0ffe0"
, , , ₃{3}₂, , , , align=left, starry polygon
, - align=center BGCOLOR="#e0f0ff"
, 2(48)3, , ₂{6}₃, , , , rowspan=2, 16, , rowspan=2, 24, , rowspan=2, {} , ,
, - align=center BGCOLOR="#e0ffe0"
, , , ₂{3}₃, , , , align=left, starry polygon

, - align=center BGCOLOR="#e0f0ff"
, G_5
3 sub>3 , , 72 , , 12 , , 3(72)3 , , ₃{4}₃, , , , 24 , , 24, , ₃{} , , align=left , self-dual, same as
$\mathbb{R}^4$ representation as {3,4,3}
, - align=center BGCOLOR="#e0f0ff"
, G_8
4 sub>4 , , 96 , , 12 , , 4(96)4 , , ₄{3}₄, , , , 24 , , 24, , ₄{}, , align=left, self-dual, same as
$\mathbb{R}^4$ representation as {3,4,3}
, - align=center BGCOLOR="#e0f0ff"
, rowspan=4, G_14
3 sub>2 , , rowspan=4, 144 , , rowspan=4, 24 , , 3(144)2 , , ₃{8}₂, , , , rowspan=2, 72 , , rowspan=2, 48, , rowspan=2, ₃{} , , align=left, same as
, - align=center BGCOLOR="#e0ffe0"
, , , ₃{8/3}₂, , , , align=left, starry polygon, same as
, - align=center BGCOLOR="#e0f0ff"
, 2(144)3, , ₂{8}₃, , , , rowspan=2, 48 , , rowspan=2, 72, , rowspan=2, {} , ,
, - align=center BGCOLOR="#e0ffe0"
, , , ₂{8/3}₃, , , , align=left, starry polygon

, - align=center BGCOLOR="#e0f0ff"
, rowspan=4, G_9
4 sub>2 , , rowspan=4, 192 , , rowspan=4, 24 , , 4(192)2 , , ₄{6}₂, , , , 96 , , 48, , ₄{} , , align=left, same as
, - align=center BGCOLOR="#e0f0ff"
, 2(192)4, , ₂{6}₄, , , , 48 , , 96, , {} , ,
, - align=center BGCOLOR="#e0ffe0"
, , , ₄{3}₂, , , , 96 , , 48, , {} , , align=left, starry polygon
, - align=center BGCOLOR="#e0ffe0"
, , , ₂{3}₄, , , , 48 , , 96, , {} , , align=left, starry polygon
, - align=center BGCOLOR="#e0f0ff"
, rowspan=4, G_10
4 sub>3 , , rowspan=4, 288 , , 24 , , 4(288)3 , , ₄{4}₃, , , , rowspan=2, 96 , , rowspan=2, 72, , rowspan=2, ₄{} , ,
, - align=center BGCOLOR="#e0ffe0"
, 12, , , , ₄{8/3}₃, , , , align=left, starry polygon
, - align=center BGCOLOR="#e0f0ff"
, 24, , 3(288)4, , ₃{4}₄, , , , rowspan=2, 72 , , rowspan=2, 96, , rowspan=2, ₃{} , ,
, - align=center BGCOLOR="#e0ffe0"
, 12, , , , ₃{8/3}₄, , , , align=left, starry polygon

, - align=center BGCOLOR="#e0f0ff"
, rowspan=2, G_20
3 sub>3 , , rowspan=2, 360 , , rowspan=2, 30 , , 3(360)3 , , ₃{5}₃, , , , rowspan=2, 120 , , rowspan=2, 120, , rowspan=2, ₃{}, , align=left , self-dual, same as
$\mathbb{R}^4$ representation as {3,3,5}
, - align=center BGCOLOR="#e0ffe0"
, , , ₃{5/2}₃, , , , align=left, self-dual, starry polygon

, - align=center BGCOLOR="#e0f0ff"
, rowspan=2, G_16
5 sub>5 , , rowspan=2, 600 , , 30 , , 5(600)5 , , ₅{3}₅, , , , rowspan=2, 120 , , rowspan=2, 120, , rowspan=2, ₅{} , , align=left , self-dual, same as
$\mathbb{R}^4$ representation as {3,3,5}
, - align=center BGCOLOR="#e0ffe0"
, 10, , , , ₅{5/2}₅, , , , align=left, self-dual, starry polygon

, - align=center BGCOLOR="#e0f0ff"
, rowspan=8, G_21
3 0sub>2 , , rowspan=8, 720 , , rowspan=8, 60 , , 3(720)2 , , ₃{10}₂, , , , rowspan=4, 360 , , rowspan=4, 240, , rowspan=4, ₃{} , , align=left, same as
, - align=center BGCOLOR="#e0ffe0"
, , , , ₃{5}₂, , , , align=left, starry polygon
, - align=center BGCOLOR="#e0ffe0"
, , , , ₃{10/3}₂, , , , align=left, starry polygon, same as
, - align=center BGCOLOR="#e0ffe0"
, , , , ₃{5/2}₂, , , , align=left, starry polygon
, - align=center BGCOLOR="#e0f0ff"
, 2(720)3, , ₂{10}₃, , , , rowspan=4, 240 , , rowspan=4, 360, , rowspan=4, {} , ,
, - align=center BGCOLOR="#e0ffe0"
, , , ₂{5}₃, , , , align=left, starry polygon
, - align=center BGCOLOR="#e0ffe0"
, , , ₂{10/3}₃, , , , align=left, starry polygon
, - align=center BGCOLOR="#e0ffe0"
, , , ₂{5/2}₃, , , , align=left, starry polygon

, - align=center BGCOLOR="#e0f0ff"
, rowspan=8, G_17
5 sub>2 , , rowspan=8, 1200 , , 60 , , 5(1200)2 , , ₅{6}₂, , , , rowspan=4, 600 , , rowspan=4, 240, , rowspan=4, ₅{} , , align=left, same as
, - align=center BGCOLOR="#e0ffe0"
, 20, , , , ₅{5}₂, , , , align=left, starry polygon
, - align=center BGCOLOR="#e0ffe0"
, 20 , , , , ₅{10/3}₂, , , , align=left, starry polygon
, - align=center BGCOLOR="#e0ffe0"
, 60, , , , ₅{3}₂, , , , align=left, starry polygon
, - align=center BGCOLOR="#e0f0ff"
, 60, , 2(1200)5, , ₂{6}₅, , , , rowspan=4, 240 , , rowspan=4, 600, , rowspan=4, {} , ,
, - align=center BGCOLOR="#e0ffe0"
, 20, , , , ₂{5}₅, , , , align=left, starry polygon
, - align=center BGCOLOR="#e0ffe0"
, 20, , , , ₂{10/3}₅, , , , align=left, starry polygon
, - align=center BGCOLOR="#e0ffe0"
, 60, , , , ₂{3}₅, , , , align=left, starry polygon

, - align=center BGCOLOR="#e0f0ff"
, rowspan=8, G_18
5 sub>3 , , rowspan=8, 1800 , , 60 , , 5(1800)3 , , ₅{4}₃, , , , rowspan=4, 600 , , rowspan=4, 360, , rowspan=4, ₅{} , , align=left,
, - align=center BGCOLOR="#e0ffe0"
, , 15 , , , , ₅{10/3}₃, , , , align=left, starry polygon
, - align=center BGCOLOR="#e0ffe0"
, , 30 , , , , ₅{3}₃, , , , align=left, starry polygon
, - align=center BGCOLOR="#e0ffe0"
, , 30 , , , , ₅{5/2}₃, , , , align=left, starry polygon

, - align=center BGCOLOR="#e0f0ff"
, 60, , 3(1800)5, , ₃{4}₅, , , , rowspan=4, 360 , , rowspan=4, 600, , rowspan=4, ₃{} , ,
, - align=center BGCOLOR="#e0ffe0"
, 15, , , , ₃{10/3}₅, , , , align=left, starry polygon
, - align=center BGCOLOR="#e0ffe0"
, 30, , , , ₃{3}₅, , , , align=left, starry polygon
, - align=center BGCOLOR="#e0ffe0"
, 30 , , , , ₃{5/2}₅, , , , align=left, starry polygon

Visualizations of regular complex polygons

Polygons of the form _''p''{2''r''}_''q'' can be visualized by ''q'' color sets of ''p''-edge. Each ''p''-edge is seen as a regular polygon, while there are no faces.

;2D orthogonal projections of complex polygons ₂{''r''}_''q'':

Polygons of the form ₂{4}_''q'' are called generalized orthoplexes. They share vertices with the 4D ''q''-''q'' duopyramids, vertices connected by 2-edges.

Complex bipartite graph square.svg, ₂{4}₂, , with 4 vertices, and 4 edges
Complex polygon 2-4-3-bipartite graph.png, ₂{4}₃, , with 6 vertices, and 9 edgesCoxeter, Regular Complex Polytopes, p. 108
Complex polygon 2-4-4 bipartite graph.png, ₂{4}₄, , with 8 vertices, and 16 edges
Complex polygon 2-4-5-bipartite graph.png, ₂{4}₅, , with 10 vertices, and 25 edges
6-generalized-2-orthoplex.svg, ₂{4}₆, , with 12 vertices, and 36 edges
7-generalized-2-orthoplex.svg, ₂{4}₇, , with 14 vertices, and 49 edges
8-generalized-2-orthoplex.svg, ₂{4}₈, , with 16 vertices, and 64 edges
9-generalized-2-orthoplex.svg, ₂{4}₉, , with 18 vertices, and 81 edges
10-generalized-2-orthoplex.svg, ₂{4}₁₀, , with 20 vertices, and 100 edges

;Complex polygons _''p''{4}₂:

Polygons of the form _''p''{4}₂ are called generalized hypercubes (squares for polygons). They share vertices with the 4D ''p''-''p'' duoprisms, vertices connected by p-edges. Vertices are drawn in green, and ''p''-edges are drawn in alternate colors, red and blue. The perspective is distorted slightly for odd dimensions to move overlapping vertices from the center.

2-generalized-2-cube.svg, ₂{4}₂, or , with 4 vertices, and 4 2-edges
3-generalized-2-cube_skew.svg, ₃{4}₂, or , with 9 vertices, and 6 (triangular) 3-edges
4-generalized-2-cube.svg, ₄{4}₂, or , with 16 vertices, and 8 (square) 4-edges
5-generalized-2-cube_skew.svg, ₅{4}₂, or , with 25 vertices, and 10 (pentagonal) 5-edges
6-generalized-2-cube.svg, ₆{4}₂, or , with 36 vertices, and 12 (hexagonal) 6-edges
7-generalized-2-cube_skew.svg, ₇{4}₂, or , with 49 vertices, and 14 (heptagonal)7-edges
8-generalized-2-cube.svg, ₈{4}₂, or , with 64 vertices, and 16 (octagonal) 8-edges
9-generalized-2-cube_skew.svg, ₉{4}₂, or , with 81 vertices, and 18 (enneagonal) 9-edges
10-generalized-2-cube.svg, ₁₀{4}₂, or , with 100 vertices, and 20 (decagonal) 10-edges

;3D perspective projections of complex polygons _''p''{4}₂. The duals ₂{4}_''p'': are seen by adding vertices inside the edges, and adding edges in place of vertices.

Complex polygon 3-4-2-stereographic3.png, ₃{4}₂, or with 9 vertices, 6 3-edges in 2 sets of colors
Complex polygon 2-4-3-stereographic0.png, ₂{4}₃, with 6 vertices, 9 edges in 3 sets
Complex polygon 4-4-2-stereographic3.svg, ₄{4}₂, or with 16 vertices, 8 4-edges in 2 sets of colors and filled square 4-edges
Complex_polygon_5-4-2-stereographic3.png, ₅{4}₂, or with 25 vertices, 10 5-edges in 2 sets of colors

;Other Complex polygons _''p''{''r''}₂:

Complex_polygon_3-6-2.png, ₃{6}₂, or , with 24 vertices in black, and 16 3-edges colored in 2 sets of 3-edges in red and blue
Complex_polygon_3-8-2.png, ₃{8}₂, or , with 72 vertices in black, and 48 3-edges colored in 2 sets of 3-edges in red and blue

;2D orthogonal projections of complex polygons, _''p''{''r''}_''p'':

Polygons of the form _''p''{''r''}_''p'' have equal number of vertices and edges. They are also self-dual.

Complex polygon 3-3-3.png, ₃{3}₃, or , with 8 vertices in black, and 8 3-edges colored in 2 sets of 3-edges in red and blue
Complex_polygon_3-4-3-fill1.png, ₃{4}₃, or , with 24 vertices and 24 3-edges shown in 3 sets of colors, one set filledCoxeter, Regular Complex Polytopes, p. 110
Complex polygon 4-3-4.png, ₄{3}₄, or , with 24 vertices and 24 4-edges shown in 4 sets of colors
Complex polygon 3-5-3.png, ₃{5}₃, or , with 120 vertices and 120 3-edges
Complex polygon 5-3-5.png, ₅{3}₅, or , with 120 vertices and 120 5-edges

Regular complex polytopes

In general, a regular complex polytope is represented by Coxeter as _''p''{''z''₁}_''q''{z₂}_''r''{z₃}_''s''… or Coxeter diagram …, having symmetry _''p'' 'z''₁sub>''q'' 'z''₂sub>''r'' 'z''₃sub>''s''… or ….

There are infinite families of regular complex polytopes that occur in all dimensions, generalizing the hypercubes and cross polytopes in real space. Shephard's "generalized orthotope" generalizes the hypercube; it has symbol given by γ = _''p''{4}₂{3}₂…₂{3}₂ and diagram …. Its symmetry group has diagram _''p'' sub>2 sub>2…₂ sub>2; in the Shephard–Todd classification, this is the group G(''p'', 1, ''n'') generalizing the signed permutation matrices. Its dual regular polytope, the "generalized cross polytope", is represented by the symbol β = ₂{3}₂{3}₂…₂{4}_''p'' and diagram ….Coxeter, Regular Complex Polytopes, pp. 118–119.

A 1-dimensional ''regular complex polytope'' in $\mathbb{C}^1$ is represented as , having ''p'' vertices, with its real representation a regular polygon, {''p''}. Coxeter also gives it symbol γ or β as 1-dimensional generalized hypercube or cross polytope. Its symmetry is _''p''[] or , a cyclic group of order ''p''. In a higher polytope, _''p''{} or represents a ''p''-edge element, with a 2-edge, {} or , representing an ordinary real edge between two vertices.

A dual complex polytope is constructed by exchanging ''k'' and (''n''-1-''k'')-elements of an ''n''-polytope. For example, a dual complex polygon has vertices centered on each edge, and new edges are centered at the old vertices. A ''v''-valence vertex creates a new ''v''-edge, and ''e''-edges become ''e''-valence vertices. The dual of a regular complex polytope has a reversed symbol. Regular complex polytopes with symmetric symbols, i.e. _''p''{''q''}_''p'', _''p''{''q''}_''r''{''q''}_''p'', _''p''{''q''}_''r''{''s''}_''r''{''q''}_''p'', etc. are self dual.

Enumeration of regular complex polyhedra

Coxeter enumerated this list of nonstarry regular complex polyhedra in $\mathbb{C}^3$, including the 5 platonic solids in $\mathbb{R}^3$.Coxeter, Regular Complex Polytopes, Table V. The nonstarry regular polyhedra and 4-polytopes. p. 180.

A regular complex polyhedron, _''p''{''n''₁}_''q''{''n''₂}_''r'' or , has faces, edges, and vertex figures.

A complex regular polyhedron _''p''{''n''₁}_''q''{''n''₂}_''r'' requires both ''g''₁ = order(_''p'' 'n''₁sub>''q'') and ''g''₂ = order(_''q'' 'n''₂sub>''r'') be finite.

Given ''g'' = order(_''p'' 'n''₁sub>''q'' 'n''₂sub>''r''), the number of vertices is ''g''/''g''₂, and the number of faces is ''g''/''g''₁. The number of edges is ''g''/''pr''.

{, class="wikitable sortable"
!Space, , Group, , data-sort-type="number", Order, , Coxeter number, , colspan=2, Polygon, , data-sort-type="number", Vertices, , colspan=2 data-sort-type="number" , Edges, , colspan=2 data-sort-type="number", Faces, , data-sort-type="number", Vertex
figure, , Van Oss
polygon, , Notes
, - align=center BGCOLOR="#ffe0e0"
, $\mathbb{R}^3$, , G(1,1,3)
₂ sub>2 sub>2
= ,3, 24 , , 4 , , α₃ = ₂{3}₂{3}₂
= {3,3}, , width=40, , , 4 , , 6, , {} , , 4, , {3} , , {3} , , none, , align=left, Real tetrahedron
Same as
, - align=center BGCOLOR="#ffe0e0"
, rowspan=2, $\mathbb{R}^3$, , rowspan=2, G_23
2 sub>2 sub>2
= ,5, , rowspan=2, 120 , , rowspan=2, 10 , , ₂{3}₂{5}₂ = {3,5}, , , , 12 , , 30, , {} , , 20, , {3} , , {5} , , none, , align=left, Real icosahedron
, - align=center BGCOLOR="#ffe0e0"
, ₂{5}₂{3}₂ = {5,3}, , , , 20 , , 30, , {} , , 12, , {5} , , {3} , , none, , align=left, Real dodecahedron

, - align=center BGCOLOR="#ffe0e0"
, $\mathbb{R}^3$ , , rowspan=2, G(2,1,3)
₂ sub>2 sub>2
= ,4, rowspan=2, 48 , , rowspan=2, 6 , , β = β₃ = {3,4}, , , , 6 , , 12, , {} , , 8 , , {3}, , {4} , , {4}, , align=left, Real octahedron
Same as {}+{}+{}, order 8
Same as , order 24
, - align=center BGCOLOR="#ffe0e0"
, $\mathbb{R}^3$, , γ = γ₃ = {4,3}, , , , 8, , 12, , {} , , 6, , {4}, , {3} , , none, , align=left, Real cube
Same as {}×{}×{} or

, - align=center BGCOLOR="#ffffe0"
, $\mathbb{C}^3$, , rowspan=2, G(p,1,3)
₂ sub>2 sub>''p''
p=2,3,4,... , , rowspan=2, 6''p''³ , , rowspan=2, 3''p'' , , β = ₂{3}₂{4}_''p'', ,           
, , 3''p'' , , 3''p''², , {} , , ''p''³, , {3} , , ₂{4}_''p'' , , ₂{4}_''p'', , align=left, Generalized octahedron
Same as _''p''{}+_''p''{}+_''p''{}, order ''p''³
Same as , order 6''p''²
, - align=center BGCOLOR="#ffffe0"
, $\mathbb{C}^3$, , γ = _''p''{4}₂{3}₂, , , , ''p''³, , 3''p''², , _''p''{} , , 3''p'', , _''p''{4}₂, , {3} , , none, , align=left, Generalized cube
Same as _''p''{}×_''p''{}×_''p''{} or

, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^3$, , rowspan=2, G(3,1,3)
₂ sub>2 sub>3 , , rowspan=2, 162 , , rowspan=2, 9 , , β = ₂{3}₂{4}₃, , , , 9 , , 27, , {} , , 27, , {3} , , ₂{4}₃ , , ₂{4}₃, , align=left, Same as ₃{}+₃{}+₃{}, order 27
Same as , order 54
, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^3$, , γ = ₃{4}₂{3}₂, , , , 27, , 27, , ₃{} , , 9, , ₃{4}₂, , {3} , , none, , align=left, Same as ₃{}×₃{}×₃{} or

, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^3$, , rowspan=2, G(4,1,3)
₂ sub>2 sub>4 , , rowspan=2, 384 , , rowspan=2, 12 , , β = ₂{3}₂{4}₄, , , , 12 , , 48 , , {} , , 64, , {3} , , ₂{4}₄ , , ₂{4}₄, , align=left, Same as ₄{}+₄{}+₄{}, order 64
Same as , order 96
, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^3$, , γ = ₄{4}₂{3}₂, , , , 64 , , 48 , , ₄{} , , 12 , , ₄{4}₂, , {3} , , none, , align=left, Same as ₄{}×₄{}×₄{} or

, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^3$, , rowspan=2, G(5,1,3)
₂ sub>2 sub>5 , , rowspan=2, 750 , , rowspan=2, 15 , , β = ₂{3}₂{4}₅, , , , 15 , , 75, , {} , , 125, , {3} , , ₂{4}₅ , , ₂{4}₅, , align=left, Same as ₅{}+₅{}+₅{}, order 125
Same as , order 150
, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^3$, , γ = ₅{4}₂{3}₂, , , , 125, , 75, , ₅{} , , 15, , ₅{4}₂, , {3} , , none, , align=left, Same as ₅{}×₅{}×₅{} or

, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^3$, , rowspan=2, G(6,1,3)
₂ sub>2 sub>6 , , rowspan=2, 1296 , , rowspan=2, 18 , , β = ₂{3}₂{4}₆, , , , 36 , , 108 , , {} , , 216, , {3} , , ₂{4}₆ , , ₂{4}₆, , align=left, Same as ₆{}+₆{}+₆{}, order 216
Same as , order 216
, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^3$, , γ = ₆{4}₂{3}₂, , , , 216, , 108, , ₆{} , , 18, , ₆{4}₂, , {3} , , none, , align=left, Same as ₆{}×₆{}×₆{} or

, - align=center BGCOLOR="#e0f0ff"
, rowspan=3, $\mathbb{C}^3$, , G_25
3 sub>3 sub>3 , , 648 , , 9 , , ₃{3}₃{3}₃, , , , 27 , , 72, , ₃{} , , 27, , ₃{3}₃ , , ₃{3}₃ , , ₃{4}₂, , align=left, Same as .
$\mathbb{R}^6$ representation as 2₂₁
Hessian polyhedron
, - align=center BGCOLOR="#e0f0ff"
, rowspan=2, G_26
2 sub>3 sub>3 , , rowspan=2, 1296, , rowspan=2, 18 , , ₂{4}₃{3}₃, , , , 54 , , 216, , {} , , 72, , ₂{4}₃ , , ₃{3}₃ , , {6} , ,
, - align=center BGCOLOR="#e0f0ff"
, ₃{3}₃{4}₂, , , , 72 , , 216, , ₃{}, , 54, , ₃{3}₃ , , ₃{4}₂ , , ₃{4}₃, , align=left, Same as
$\mathbb{R}^6$ representation as 1₂₂

Visualizations of regular complex polyhedra

;2D orthogonal projections of complex polyhedra, _''p''{''s''}_''t''{''r''}_''r'':

3-simplex t0.svg, Real {3,3}, or has 4 vertices, 6 edges, and 4 faces
Complex polyhedron 3-3-3-3-3-one-blue-face.png, ₃{3}₃{3}₃, or , has 27 vertices, 72 3-edges, and 27 faces, with one face highlighted blue.Coxeter, Regular Complex Polytopes, p. 131
Complex polyhedron 2-4-3-3-3_blue-edge.png, ₂{4}₃{3}₃, has 54 vertices, 216 simple edges, and 72 faces, with one face highlighted blue.
Complex polyhedron 3-3-3-4-2-one-blue-face.png, ₃{3}₃{4}₂, or , has 72 vertices, 216 3-edges, and 54 vertices, with one face highlighted blue.

;Generalized octahedra

Generalized octahedra have a regular construction as and quasiregular form as . All elements are simplexes.

Complex tripartite graph octahedron.svg, Real {3,4}, or , with 6 vertices, 12 edges, and 8 faces
3-generalized-3-orthoplex-tripartite.svg, ₂{3}₂{4}₃, or , with 9 vertices, 27 edges, and 27 faces
4-generalized-3-orthoplex.svg, ₂{3}₂{4}₄, or , with 12 vertices, 48 edges, and 64 faces
5-generalized-3-orthoplex.svg, ₂{3}₂{4}₅, or , with 15 vertices, 75 edges, and 125 faces
6-generalized-3-orthoplex.svg, ₂{3}₂{4}₆, or , with 18 vertices, 108 edges, and 216 faces
7-generalized-3-orthoplex.svg, ₂{3}₂{4}₇, or , with 21 vertices, 147 edges, and 343 faces
8-generalized-3-orthoplex.svg, ₂{3}₂{4}₈, or , with 24 vertices, 192 edges, and 512 faces
9-generalized-3-orthoplex.svg, ₂{3}₂{4}₉, or , with 27 vertices, 243 edges, and 729 faces
10-generalized-3-orthoplex.svg, ₂{3}₂{4}₁₀, or , with 30 vertices, 300 edges, and 1000 faces

;Generalized cubes

Generalized cubes have a regular construction as and prismatic construction as , a product of three ''p''-gonal 1-polytopes. Elements are lower dimensional generalized cubes.

2-generalized-3-cube.svg, Real {4,3}, or has 8 vertices, 12 edges, and 6 faces
3-generalized-3-cube.svg, ₃{4}₂{3}₂, or has 27 vertices, 27 3-edges, and 9 faces
4-generalized-3-cube.svg, ₄{4}₂{3}₂, or , with 64 vertices, 48 edges, and 12 faces
5-generalized-3-cube.svg, ₅{4}₂{3}₂, or , with 125 vertices, 75 edges, and 15 faces
6-generalized-3-cube.svg, ₆{4}₂{3}₂, or , with 216 vertices, 108 edges, and 18 faces
7-generalized-3-cube.svg, ₇{4}₂{3}₂, or , with 343 vertices, 147 edges, and 21 faces
8-generalized-3-cube.svg, ₈{4}₂{3}₂, or , with 512 vertices, 192 edges, and 24 faces
9-generalized-3-cube.svg, ₉{4}₂{3}₂, or , with 729 vertices, 243 edges, and 27 faces
10-generalized-3-cube.svg, ₁₀{4}₂{3}₂, or , with 1000 vertices, 300 edges, and 30 faces

Enumeration of regular complex 4-polytopes

Coxeter enumerated this list of nonstarry regular complex 4-polytopes in $\mathbb{C}^4$, including the 6 convex regular 4-polytopes in $\mathbb{R}^4$.
{, class="wikitable sortable"
!Space, , Group, , data-sort-type="number", Order, , Coxeter
number, , Polytope, , data-sort-type="number", Vertices, , data-sort-type="number", Edges, , data-sort-type="number", Faces, , data-sort-type="number", Cells, , Van Oss
polygon, , Notes

, - align=center BGCOLOR="#ffe0e0"
, $\mathbb{R}^4$, , G(1,1,4)
₂ sub>2 sub>2 sub>2
= ,3,3, 120, , 5 , , α₄ = ₂{3}₂{3}₂{3}₂
= {3,3,3}
, , 5 , , 10
{} , , 10
{3} , , 5
{3,3} , , none, , align=left, Real 5-cell (simplex)
, - align=center BGCOLOR="#ffe0e0"
, rowspan=3, $\mathbb{R}^4$, , G_28
2 sub>2 sub>2 sub>2
= ,4,3, , 1152 , , 12, , ₂{3}₂{4}₂{3}₂ = {3,4,3}
, , 24 , , 96
{} , , 96
{3} , , 24
{3,4} , , {6}, , align=left, Real 24-cell
, - align=center BGCOLOR="#ffe0e0"
, rowspan=2, G_30
2 sub>2 sub>2 sub>2
= ,3,5, , rowspan=2, 14400 , , rowspan=2, 30, , ₂{3}₂{3}₂{5}₂ = {3,3,5}
, , 120 , , 720
{} , , 1200
{3} , , 600
{3,3} , , rowspan=2, {10}, , align=left, Real 600-cell
, - align=center BGCOLOR="#ffe0e0"
, ₂{5}₂{3}₂{3}₂ = {5,3,3}
, , 600 , , 1200
{} , , 720
{5}, , 120
{5,3} , , align=left, Real 120-cell
, - align=center BGCOLOR="#ffe0e0"
, $\mathbb{R}^4$, , rowspan=2, G(2,1,4)
₂ sub>2 sub>2 sub>''p''
= ,3,4, , rowspan=2, 384 , , rowspan=2, 8 , , β = β₄ = {3,3,4}
, , 8, , 24
{} , , 32
{3}, , 16
{3,3} , , {4} , , align=left, Real 16-cell
Same as , order 192

, - align=center BGCOLOR="#ffe0e0"
, $\mathbb{R}^4$, , γ = γ₄ = {4,3,3}
, , 16 , , 32
{} , , 24
{4} , , 8
{4,3} , , none, , align=left, Real tesseract
Same as {}⁴ or , order 16

, - align=center BGCOLOR="#ffffe0"
, $\mathbb{C}^4$, , rowspan=2, G(p,1,4)
₂ sub>2 sub>2 sub>''p''
p=2,3,4,... , , rowspan=2, 24''p''⁴ , , rowspan=2, 4''p'' , , β = ₂{3}₂{3}₂{4}_''p''
, , 4''p'', , 6''p''²
{} , , 4''p''³
{3}, , ''p''⁴
{3,3} , , ₂{4}_''p'', , align=left, Generalized 4- orthoplex
Same as , order 24''p''³
, - align=center BGCOLOR="#ffffe0"
, $\mathbb{C}^4$, , γ = _''p''{4}₂{3}₂{3}₂
, , ''p''⁴, , 4''p''³
_''p''{} , , 6''p''²
_''p''{4}₂ , , 4''p''
_p{4}₂{3}₂ , , none, , align=left, Generalized tesseract
Same as _''p''{}⁴ or , order ''p''⁴

, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^4$, , rowspan=2, G(3,1,4)
₂ sub>2 sub>2 sub>3 , , rowspan=2, 1944 , , rowspan=2, 12 , , β = ₂{3}₂{3}₂{4}₃
, , 12, , 54
{} , , 108
{3}, , 81
{3,3} , , ₂{4}₃, , align=left, Generalized 4- orthoplex
Same as , order 648
, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^4$, , γ = ₃{4}₂{3}₂{3}₂
, , 81, , 108
₃{} , , 54
₃{4}₂ , , 12
₃{4}₂{3}₂ , , none, , align=left, Same as ₃{}⁴ or , order 81

, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^4$, , rowspan=2, G(4,1,4)
₂ sub>2 sub>2 sub>4 , , rowspan=2, 6144 , , rowspan=2, 16 , , β = ₂{3}₂{3}₂{4}₄
, , 16, , 96
{} , , 256
{3}, , 64
{3,3}
, , ₂{4}₄, , align=left, Same as , order 1536
, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^4$, , γ = ₄{4}₂{3}₂{3}₂

, , 256, , 256
₄{} , , 96
₄{4}₂ , , 16
₄{4}₂{3}₂ , , none, , align=left, Same as ₄{}⁴ or , order 256

, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^4$, , rowspan=2, G(5,1,4)
₂ sub>2 sub>2 sub>5 , , rowspan=2, 15000 , , rowspan=2, 20 , , β = ₂{3}₂{3}₂{4}₅
, , 20, , 150
{} , , 500
{3}, , 625
{3,3} , , ₂{4}₅, , align=left, Same as , order 3000
, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^4$, , γ = ₅{4}₂{3}₂{3}₂
, , 625, , 500
₅{} , , 150
₅{4}₂ , , 20
₅{4}₂{3}₂ , , none, , align=left, Same as ₅{}⁴ or , order 625

, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^4$, , rowspan=2, G(6,1,4)
₂ sub>2 sub>2 sub>6 , , rowspan=2, 31104 , , rowspan=2, 24 , , β = ₂{3}₂{3}₂{4}₆
, , 24, , 216
{} , , 864
{3}, , 1296
{3,3} , , ₂{4}₆, , align=left, Same as , order 5184
, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^4$, , γ = ₆{4}₂{3}₂{3}₂
, , 1296, , 864
₆{} , , 216
₆{4}₂ , , 24
₆{4}₂{3}₂ , , none, , align=left, Same as ₆{}⁴ or , order 1296

, - align=center BGCOLOR="#e0f0ff"
, $\mathbb{C}^4$, , G_32
3 sub>3 sub>3 sub>3 , , 155520, , rowspan=2, 30, , ₃{3}₃{3}₃{3}₃
, , 240 , , 2160
₃{} , , 2160
₃{3}₃ , , 240
₃{3}₃{3}₃ , , ₃{4}₃, , align=left, Witting polytope
$\mathbb{R}^8$ representation as 4₂₁

Visualizations of regular complex 4-polytopes

4-simplex t0.svg, Real {3,3,3}, , had 5 vertices, 10 edges, 10 {3} faces, and 5 {3,3} cells
24-cell t0 F4.svg, Real {3,4,3}, , had 24 vertices, 96 edges, 96 {3} faces, and 24 {3,4} cells
120-cell graph H4.svg, Real {5,3,3}, , had 600 vertices, 1200 edges, 720 {5} faces, and 120 {5,3} cells
600-cell graph H4.svg, Real {3,3,5}, , had 120 vertices, 720 edges, 1200 {3} faces, and 600 {3,3} cells
Witting_polytope.png, Witting polytope, , has 240 vertices, 2160 3-edges, 2160 3{3}3 faces, and 240 3{3}3{3}3 cells

;Generalized 4-orthoplexes
Generalized 4-orthoplexes have a regular construction as and quasiregular form as . All elements are simplexes.

Complex multipartite graph 16-cell.svg, Real {3,3,4}, or , with 8 vertices, 24 edges, 32 faces, and 16 cells
3-generalized-4-orthoplex.svg, ₂{3}₂{3}₂{4}₃, or , with 12 vertices, 54 edges, 108 faces, and 81 cells
4-generalized-4-orthoplex.svg, ₂{3}₂{3}₂{4}₄, or , with 16 vertices, 96 edges, 256 faces, and 256 cells
5-generalized-4-orthoplex.svg, ₂{3}₂{3}₂{4}₅, or , with 20 vertices, 150 edges, 500 faces, and 625 cells
6-generalized-4-orthoplex.svg, ₂{3}₂{3}₂{4}₆, or , with 24 vertices, 216 edges, 864 faces, and 1296 cells
7-generalized-4-orthoplex.svg, ₂{3}₂{3}₂{4}₇, or , with 28 vertices, 294 edges, 1372 faces, and 2401 cells
8-generalized-4-orthoplex.svg, ₂{3}₂{3}₂{4}₈, or , with 32 vertices, 384 edges, 2048 faces, and 4096 cells
9-generalized-4-orthoplex.svg, ₂{3}₂{3}₂{4}₉, or , with 36 vertices, 486 edges, 2916 faces, and 6561 cells
10-generalized-4-orthoplex.svg, ₂{3}₂{3}₂{4}₁₀, or , with 40 vertices, 600 edges, 4000 faces, and 10000 cells

;Generalized 4-cubes

Generalized tesseracts have a regular construction as and prismatic construction as , a product of four ''p''-gonal 1-polytopes. Elements are lower dimensional generalized cubes.

2-generalized-4-cube.svg, Real {4,3,3}, or , with 16 vertices, 32 edges, 24 faces, and 8 cells
3-generalized-4-cube.svg, ₃{4}₂{3}₂{3}₂, or , with 81 vertices, 108 edges, 54 faces, and 12 cells
4-generalized-4-cube.svg, ₄{4}₂{3}₂{3}₂, or , with 256 vertices, 96 edges, 96 faces, and 16 cells
5-generalized-4-cube.svg, ₅{4}₂{3}₂{3}₂, or , with 625 vertices, 500 edges, 150 faces, and 20 cells
6-generalized-4-cube.svg, ₆{4}₂{3}₂{3}₂, or , with 1296 vertices, 864 edges, 216 faces, and 24 cells
7-generalized-4-cube.svg, ₇{4}₂{3}₂{3}₂, or , with 2401 vertices, 1372 edges, 294 faces, and 28 cells
8-generalized-4-cube.svg, ₈{4}₂{3}₂{3}₂, or , with 4096 vertices, 2048 edges, 384 faces, and 32 cells
9-generalized-4-cube.svg, ₉{4}₂{3}₂{3}₂, or , with 6561 vertices, 2916 edges, 486 faces, and 36 cells
10-generalized-4-cube.svg, ₁₀{4}₂{3}₂{3}₂, or , with 10000 vertices, 4000 edges, 600 faces, and 40 cells

Enumeration of regular complex 5-polytopes

Regular complex 5-polytopes in $\mathbb{C}^5$ or higher exist in three families, the real simplexes and the generalized hypercube, and orthoplex.

{, class="wikitable sortable"
!Space, , Group, , data-sort-type="number", Order, , Polytope, , data-sort-type="number", Vertices, , data-sort-type="number", Edges, , data-sort-type="number", Faces, , data-sort-type="number", Cells, , data-sort-type="number", 4-faces, , Van Oss
polygon, , Notes
, - align=center BGCOLOR="#ffe0e0"
, $\mathbb{R}^5$, , G(1,1,5)
= ,3,3,3, 720 , , α₅ = {3,3,3,3}
, , 6 , , 15
{} , , 20
{3} , , 15
{3,3}, , 6
{3,3,3} , , none, , align=left, Real 5-simplex
, - align=center BGCOLOR="#ffe0e0"
, $\mathbb{R}^5$, , rowspan=2, G(2,1,5)
= ,3,3,4, , rowspan=2, 3840 , , β = β₅ = {3,3,3,4}
, , 10, , 40
{} , , 80
{3}, , 80
{3,3} , , 32
{3,3,3} , , {4}, , align=left, Real 5-orthoplex
Same as , order 1920
, - align=center BGCOLOR="#ffe0e0"
, $\mathbb{R}^5$, , γ = γ₅ = {4,3,3,3}
, , 32 , , 80
{} , , 80
{4} , , 40
{4,3}, , 10
{4,3,3} , , none, , align=left, Real 5-cube
Same as {}⁵ or , order 32

, - align=center BGCOLOR="#ffffe0"
, $\mathbb{C}^5$, , rowspan=2, G(p,1,5)
₂ sub>2 sub>2 sub>2 sub>''p'' , , rowspan=2, 120''p''⁵ , , β = ₂{3}₂{3}₂{3}₂{4}_''p''
, , 5''p'', , 10''p''²
{} , , 10''p''³
{3}, , 5''p''⁴
{3,3} , , ''p''⁵
{3,3,3} , , ₂{4}_''p'', , align=left, Generalized 5-orthoplex
Same as , order 120''p''⁴
, - align=center BGCOLOR="#ffffe0"
, $\mathbb{C}^5$, , γ = _''p''{4}₂{3}₂{3}₂{3}₂
, , ''p''⁵ , , 5''p''⁴
_''p''{} , , 10''p''³
_''p''{4}₂ , , 10''p''²
_''p''{4}₂{3}₂, , 5''p''
_''p''{4}₂{3}₂{3}₂ , , none, , align=left, Generalized 5-cube
Same as _''p''{}⁵ or , order ''p''⁵

, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^5$, , rowspan=2, G(3,1,5)
₂ sub>2 sub>2 sub>2 sub>3 , , rowspan=2, 29160 , , β = ₂{3}₂{3}₂{3}₂{4}₃
, , 15, , 90
{} , , 270
{3}, , 405
{3,3} , , 243
{3,3,3} , , ₂{4}₃, , align=left, Same as , order 9720
, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^5$, , γ = ₃{4}₂{3}₂{3}₂{3}₂
, , 243 , , 405
₃{} , , 270
₃{4}₂ , , 90
₃{4}₂{3}₂, , 15
₃{4}₂{3}₂{3}₂ , , none, , align=left, Same as ₃{}⁵ or , order 243

, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^5$, , rowspan=2, G(4,1,5)
₂ sub>2 sub>2 sub>2 sub>4 , , rowspan=2, 122880 , , β = ₂{3}₂{3}₂{3}₂{4}₄
, , 20, , 160
{} , , 640
{3}, , 1280
{3,3} , , 1024
{3,3,3} , , ₂{4}₄, , align=left, Same as , order 30720
, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^5$, , γ = ₄{4}₂{3}₂{3}₂{3}₂
, , 1024 , , 1280
₄{} , , 640
₄{4}₂ , , 160
₄{4}₂{3}₂, , 20
₄{4}₂{3}₂{3}₂ , , none, , align=left, Same as ₄{}⁵ or , order 1024

, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^5$, , rowspan=2, G(5,1,5)
₂ sub>2 sub>2 sub>2 sub>5 , , rowspan=2, 375000 , , β = ₂{3}₂{3}₂{3}₂{5}₅
, , 25, , 250
{} , , 1250
{3}, , 3125
{3,3} , , 3125
{3,3,3} , , ₂{5}₅, , align=left, Same as , order 75000
, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^5$, , γ = ₅{4}₂{3}₂{3}₂{3}₂
, , 3125 , , 3125
₅{} , , 1250
₅{5}₂ , , 250
₅{5}₂{3}₂, , 25
₅{4}₂{3}₂{3}₂ , , none, , align=left, Same as ₅{}⁵ or , order 3125

, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^5$, , rowspan=2, G(6,1,5)
₂ sub>2 sub>2 sub>2 sub>6 , , rowspan=2, 933210 , , β = ₂{3}₂{3}₂{3}₂{4}₆
, , 30, , 360
{} , , 2160
{3}, , 6480
{3,3} , , 7776
{3,3,3} , , ₂{4}₆, , align=left, Same as , order 155520
, - align=center BGCOLOR="#e0ffff"
, $\mathbb{C}^5$, , γ = ₆{4}₂{3}₂{3}₂{3}₂
, , 7776 , , 6480
₆{} , , 2160
₆{4}₂ , , 360
₆{4}₂{3}₂, , 30
₆{4}₂{3}₂{3}₂ , , none, , align=left, Same as ₆{}⁵ or , order 7776

Visualizations of regular complex 5-polytopes

;Generalized 5-orthoplexes
Generalized 5-orthoplexes have a regular construction as and quasiregular form as . All elements are simplexes.

2-generalized-5-orthoplex.svg, Real {3,3,3,4}, , with 10 vertices, 40 edges, 80 faces, 80 cells, and 32 4-faces
3-generalized-5-orthoplex.svg, ₂{3}₂{3}₂{3}₂{4}₃, , with 15 vertices, 90 edges, 270 faces, 405 cells, and 243 4-faces
4-generalized-5-orthoplex.svg, ₂{3}₂{3}₂{3}₂{4}₄, , with 20 vertices, 160 edges, 640 faces, 1280 cells, and 1024 4-faces
5-generalized-5-orthoplex.svg, ₂{3}₂{3}₂{3}₂{4}₅, , with 25 vertices, 250 edges, 1250 faces, 3125 cells, and 3125 4-faces
6-generalized-5-orthoplex.svg, ₂{3}₂{3}₂{3}₂{4}₆, , with 30 vertices, 360 edges, 2160 faces, 6480 cells, 7776 4-faces
7-generalized-5-orthoplex.svg, ₂{3}₂{3}₂{3}₂{4}₇, , with 35 vertices, 490 edges, 3430 faces, 12005 cells, 16807 4-faces
8-generalized-5-orthoplex.svg, ₂{3}₂{3}₂{3}₂{4}₈, , with 40 vertices, 640 edges, 5120 faces, 20480 cells, 32768 4-faces
9-generalized-5-orthoplex.svg, ₂{3}₂{3}₂{3}₂{4}₉, , with 45 vertices, 810 edges, 7290 faces, 32805 cells, 59049 4-faces
10-generalized-5-orthoplex.svg, ₂{3}₂{3}₂{3}₂{4}₁₀, , with 50 vertices, 1000 edges, 10000 faces, 50000 cells, 100000 4-faces

;Generalized 5-cubes

Generalized 5-cubes have a regular construction as and prismatic construction as , a product of five ''p''-gonal 1-polytopes. Elements are lower dimensional generalized cubes.

2-generalized-5-cube.svg, Real {4,3,3,3}, , with 32 vertices, 80 edges, 80 faces, 40 cells, and 10 4-faces
3-generalized-5-cube.svg, ₃{4}₂{3}₂{3}₂{3}₂, , with 243 vertices, 405 edges, 270 faces, 90 cells, and 15 4-faces
4-generalized-5-cube.svg, ₄{4}₂{3}₂{3}₂{3}₂, , with 1024 vertices, 1280 edges, 640 faces, 160 cells, and 20 4-faces
5-generalized-5-cube.svg, ₅{4}₂{3}₂{3}₂{3}₂, , with 3125 vertices, 3125 edges, 1250 faces, 250 cells, and 25 4-faces
6-generalized-5-cube.svg, ₆{4}₂{3}₂{3}₂{3}₂, , with 7776 vertices, 6480 edges, 2160 faces, 360 cells, and 30 4-faces

Enumeration of regular complex 6-polytopes

{, class="wikitable sortable"
!Space, , Group, , data-sort-type="number", Order, , Polytope, , data-sort-type="number", Vertices, , data-sort-type="number", Edges, , data-sort-type="number", Faces, , data-sort-type="number", Cells, , data-sort-type="number", 4-faces, , data-sort-type="number", 5-faces, , Van Oss
polygon, , Notes
, - align=center BGCOLOR="#ffe0e0"
, $\mathbb{R}^6$, , G(1,1,6)
= ,3,3,3,3, 720 , , α₆ = {3,3,3,3,3}
, , 7 , , 21
{} , , 35
{3} , , 35
{3,3}, , 21
{3,3,3}, , 7
{3,3,3,3} , , none, , align=left, Real 6-simplex
, - align=center BGCOLOR="#ffe0e0"
, $\mathbb{R}^6$, , rowspan=2, G(2,1,6)
,3,3,4, rowspan=2, 46080 , , β = β₆ = {3,3,3,4}
, , 12, , 60
{} , , 160
{3}, , 240
{3,3} , , 192
{3,3,3}, , 64
{3,3,3,3} , , {4}, , align=left, Real 6-orthoplex
Same as , order 23040
, - align=center BGCOLOR="#ffe0e0"
, $\mathbb{R}^6$, , γ = γ₆ = {4,3,3,3}
, , 64 , , 192
{} , , 240
{4} , , 160
{4,3}, , 60
{4,3,3}, , 12
{4,3,3,3} , , none, , align=left, Real 6-cube
Same as {}⁶ or , order 64

, - align=center BGCOLOR="#ffffe0"
, $\mathbb{C}^6$, , rowspan=2, G(p,1,6)
₂ sub>2 sub>2 sub>2 sub>''p'' , , rowspan=2, 720''p''⁶ , , β = ₂{3}₂{3}₂{3}₂{4}_''p''
, , 6''p'', , 15''p''²
{} , , 20''p''³
{3}, , 15''p''⁴
{3,3} , , 6''p''⁵
{3,3,3}, , ''p''⁶
{3,3,3,3} , , ₂{4}_''p'', , align=left, Generalized 6-orthoplex
Same as , order 720''p''⁵
, - align=center BGCOLOR="#ffffe0"
, $\mathbb{C}^6$, , γ = _''p''{4}₂{3}₂{3}₂{3}₂
, , ''p''⁶ , , 6''p''⁵
_''p''{} , , 15''p''⁴
_''p''{4}₂ , , 20''p''³
_''p''{4}₂{3}₂, , 15''p''²
_''p''{4}₂{3}₂{3}₂, , 6''p''
_''p''{4}₂{3}₂{3}₂{3}₂ , , none, , align=left, Generalized 6-cube
Same as _''p''{}⁶ or , order ''p''⁶

Visualizations of regular complex 6-polytopes

;Generalized 6-orthoplexes
Generalized 6-orthoplexes have a regular construction as and quasiregular form as . All elements are simplexes.

2-generalized-6-orthoplex.svg, Real {3,3,3,3,4}, , with 12 vertices, 60 edges, 160 faces, 240 cells, 192 4-faces, and 64 5-faces
3-generalized-6-orthoplex.svg, ₂{3}₂{3}₂{3}₂{3}₂{4}₃, , with 18 vertices, 135 edges, 540 faces, 1215 cells, 1458 4-faces, and 729 5-faces
4-generalized-6-orthoplex.svg, ₂{3}₂{3}₂{3}₂{3}₂{4}₄, , with 24 vertices, 240 edges, 1280 faces, 3840 cells, 6144 4-faces, and 4096 5-faces
5-generalized-6-orthoplex.svg, ₂{3}₂{3}₂{3}₂{3}₂{4}₅, , with 30 vertices, 375 edges, 2500 faces, 9375 cells, 18750 4-faces, and 15625 5-faces
6-generalized-6-orthoplex.svg, ₂{3}₂{3}₂{3}₂{3}₂{4}₆, , with 36 vertices, 540 edges, 4320 faces, 19440 cells, 46656 4-faces, and 46656 5-faces
7-generalized-6-orthoplex.svg, ₂{3}₂{3}₂{3}₂{3}₂{4}₇, , with 42 vertices, 735 edges, 6860 faces, 36015 cells, 100842 4-faces, 117649 5-faces
8-generalized-6-orthoplex.svg, ₂{3}₂{3}₂{3}₂{3}₂{4}₈, , with 48 vertices, 960 edges, 10240 faces, 61440 cells, 196608 4-faces, 262144 5-faces
9-generalized-6-orthoplex.svg, ₂{3}₂{3}₂{3}₂{3}₂{4}₉, , with 54 vertices, 1215 edges, 14580 faces, 98415 cells, 354294 4-faces, 531441 5-faces
10-generalized-6-orthoplex.svg, ₂{3}₂{3}₂{3}₂{3}₂{4}₁₀, , with 60 vertices, 1500 edges, 20000 faces, 150000 cells, 600000 4-faces, 1000000 5-faces

;Generalized 6-cubes

Generalized 6-cubes have a regular construction as and prismatic construction as , a product of six ''p''-gonal 1-polytopes. Elements are lower dimensional generalized cubes.

2-generalized-6-cube.svg, Real {3,3,3,3,3,4}, , with 64 vertices, 192 edges, 240 faces, 160 cells, 60 4-faces, and 12 5-faces
3-generalized-6-cube.svg, ₃{4}₂{3}₂{3}₂{3}₂{3}₂, , with 729 vertices, 1458 edges, 1215 faces, 540 cells, 135 4-faces, and 18 5-faces
4-generalized-6-cube.svg, ₄{4}₂{3}₂{3}₂{3}₂{3}₂, , with 4096 vertices, 6144 edges, 3840 faces, 1280 cells, 240 4-faces, and 24 5-faces
5-generalized-6-cube.svg, ₅{4}₂{3}₂{3}₂{3}₂{3}₂, , with 15625 vertices, 18750 edges, 9375 faces, 2500 cells, 375 4-faces, and 30 5-faces

Enumeration of regular complex apeirotopes

Coxeter enumerated this list of nonstarry regular complex apeirotopes or honeycombs.

For each dimension there are 12 apeirotopes symbolized as δ exists in any dimensions $\mathbb{C}^n$, or $\mathbb{R}^n$ if ''p''=''q''=2. Coxeter calls these generalized cubic honeycombs for ''n''>2.

Each has proportional element counts given as:
:k-faces = ${n \choose k}p^{n-k}r^k$, where ${n \choose m}=\frac{n!}{m!\,(n-m)!}$ and ''n''! denotes the factorial of ''n''.

Regular complex 1-polytopes

The only regular complex 1-polytope is _∞{}, or . Its real representation is an apeirogon, {∞}, or .

Regular complex apeirogons

Rank 2 complex apeirogons have symmetry _''p'' 'q''sub>''r'', where 1/''p'' + 2/''q'' + 1/''r'' = 1. Coxeter expresses them as δ where ''q'' is constrained to satisfy .

There are 8 solutions:
{, class=wikitable
, ₂ infin;sub>2, , ₃ 2sub>2, , ₄ sub>2, , ₆ sub>2, , ₃ sub>3, , ₆ sub>3, , ₄ sub>4, , ₆ sub>6
, - align=center
, , , , , , , , , , , , , , ,

There are two excluded solutions odd ''q'' and unequal ''p'' and ''r'': ₁₀ sub>2 and ₁₂ sub>4, or and .

A regular complex apeirogon _''p''{''q''}_''r'' has ''p''-edges and ''r''-gonal vertex figures. The dual apeirogon of _''p''{''q''}_''r'' is _''r''{''q''}_''p''. An apeirogon of the form _''p''{''q''}_''p'' is self-dual. Groups of the form _''p'' ''q''sub>2 have a half symmetry _''p'' 'q''sub>''p'', so a regular apeirogon is the same as quasiregular .

Apeirogons can be represented on the Argand plane share four different vertex arrangements. Apeirogons of the form ₂{''q''}_''r'' have a vertex arrangement as {''q''/2,''p''}. The form _''p''{''q''}₂ have vertex arrangement as r{''p'',''q''/2}. Apeirogons of the form _''p''{4}_''r'' have vertex arrangements {''p'',''r''}.

Including affine nodes, and $\mathbb{C}^2$, there are 3 more infinite solutions: _∞ sub>∞, _∞ sub>2, _∞ sub>3, and , , and . The first is an index 2 subgroup of the second. The vertices of these apeirogons exist in $\mathbb{C}^1$.

{, class="wikitable sortable"
, + Rank 2
!Space, , Group, , colspan=2, Apeirogon, , Edge, , $\mathbb{R}^2$ rep., , Picture, , Notes
, - align=center BGCOLOR="#ffe0e0"
, $\mathbb{R}^1$, , ₂ infin;sub>2 = infin;, δ = {∞} , ,        
, , {} , , , , , , align=left, Real apeirogon
Same as
, - align=center BGCOLOR="#f0e0ff"
, $\mathbb{C}^2$ / $\mathbb{C}^1$, , _∞ sub>2, , _∞{4}₂ , , , , _∞{} , , {4,4} , , , , align=left, Same as
, - align=center BGCOLOR="#f0e0ff"
, $\mathbb{C}^1$, , _∞ sub>3, , _∞{3}₃ , , , , _∞{} , , {3,6} , , , , align=left, Same as

, - align=center BGCOLOR="#f0fff0"
, $\mathbb{C}^1$, , _''p'' 'q''sub>''r'', , δ = _''p''{''q''}_''r'' , , , , _''p''{} , , , , , , align=left,

, - align=center BGCOLOR="#e0f0ff"
, rowspan=2, $\mathbb{C}^1$, , rowspan=2, ₃ 2sub>2, , δ = ₃{12}₂ , , , , ₃{}, , r{3,6}, , , , align=left, Same as

, - align=center BGCOLOR="#e0f0ff"
, , δ = ₂{12}₃ , , , , {}, , {6,3}, , , , align=left,
, - align=center BGCOLOR="#e0f0ff"
, $\mathbb{C}^1$, , ₃ sub>3, , δ = ₃{6}₃ , , , , ₃{} , , {3,6}, , , , align=left, Same as

, - align=center BGCOLOR="#e0f0ff"
, rowspan=2, $\mathbb{C}^1$, , rowspan=2, ₄ sub>2, , δ = ₄{8}₂ , , , , ₄{}, , {4,4}, , , , align=left, Same as
, - align=center BGCOLOR="#e0f0ff"
, , δ = ₂{8}₄ , , , , {} , , {4,4}, , , , align=left,

, - align=center BGCOLOR="#e0f0ff"
, $\mathbb{C}^1$, , ₄ sub>4, , δ = ₄{4}₄ , , , , ₄{} , , {4,4}, , , , align=left, Same as

, - align=center BGCOLOR="#e0f0ff"
, rowspan=2, $\mathbb{C}^1$, , rowspan=2, ₆ sub>2, , δ = ₆{6}₂ , , , , ₆{}, , r{3,6}, , , , align=left, Same as
, - align=center BGCOLOR="#e0f0ff"
, , δ = ₂{6}₆ , , , , {} , , {3,6}, , , , align=left,

, - align=center BGCOLOR="#e0f0ff"
, rowspan=2, $\mathbb{C}^1$, , rowspan=2, ₆ sub>3, , δ = ₆{4}₃ , , , , ₆{}, , {6,3}, , , , align=left,
, - align=center BGCOLOR="#e0f0ff"
, , δ = ₃{4}₆ , , , , ₃{}, , {3,6}, , , , align=left,

, - align=center BGCOLOR="#e0f0ff"
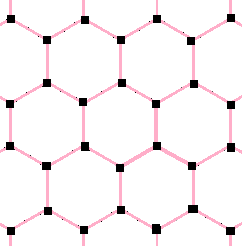, $\mathbb{C}^1$, , ₆ sub>6, , δ = ₆{3}₆ , , , , ₆{}, , {3,6}, , , , align=left, Same as

Regular complex apeirohedra

There are 22 regular complex apeirohedra, of the form _''p''{''a''}_''q''{''b''}_''r''. 8 are self-dual (''p''=''r'' and ''a''=''b''), while 14 exist as dual polytope pairs. Three are entirely real (''p''=''q''=''r''=2).

Coxeter symbolizes 12 of them as δ or _''p''{4}₂{4}_''r'' is the regular form of the product apeirotope δ × δ or _''p''{''q''}_''r'' × _''p''{''q''}_''r'', where ''q'' is determined from ''p'' and ''r''.

is the same as , as well as , for ''p'',''r''=2,3,4,6. Also = .

{, class=wikitable
, + Rank 3
!Space, , Group, , colspan=2, Apeirohedron, , Vertex, , colspan=2, Edge, , colspan=2, Face, , van Oss
apeirogon, , Notes

, - align=center BGCOLOR="#f0e0ff"
, $\mathbb{C}^3$, , ₂ sub>2 sub>∞ , , _∞{4}₂{3}₂, , , , , , , , _∞{} , , , , _∞{4}₂, , , , align=left, Same as _∞{}×_∞{}×_∞{} or
Real representation {4,3,4}

, - align=center BGCOLOR="#ffffe0"
, $\mathbb{C}^2$, , _''p'' sub>2 sub>''r'', , _''p''{4}₂{4}_''r'', ,            
, , ''p''², , 2''pq'', , _''p''{}, , ''r''², , _''p''{4}₂, , ₂{''q''}_''r'', , align=left, Same as , ''p'',''r''=2,3,4,6

, - align=center BGCOLOR="#ffe0e0"
, $\mathbb{R}^2$, , ,4, δ = {4,4}, , , , 4, , 8, , {}, , 4, , {4}, , {∞}, , align=left, Real square tiling
Same as or or

, - align=center BGCOLOR="#e0f0ff"
, $\mathbb{C}^2$
, valign=top, ₃ sub>2 sub>2
 
₃ sub>2 sub>3
₄ sub>2 sub>2
 
₄ sub>2 sub>4
₆ sub>2 sub>2
 
₆ sub>2 sub>3
 
₆ sub>2 sub>6
, valign=top, ₃{4}₂{4}_2
2{4}₂{4}_3
3{4}₂{4}_3
4{4}₂{4}_2
2{4}₂{4}_4
4{4}₂{4}_4
6{4}₂{4}_2
2{4}₂{4}_6
6{4}₂{4}_3
3{4}₂{4}_6
6{4}₂{4}₆
, valign=top ,










, valign=top , 9
4
9
16
4
16
36
4
36
9
36
, valign=top , 12
12
18
16
16
32
24
24
36
36
72
, valign=top , ₃{}
{}
₃{}
₄{}
{}
₄{}
₆{}
{}
₆{}
₃{}
₆{}
, valign=top , 4
9
9
4
16
16
4
36
9
36
36
, valign=top , ₃{4}₂
{4}
₃{4}_2
4{4}₂
{4}
₄{4}_2
6{4}₂
{4}
₆{4}_2
3{4}_2
6{4}₂, , _''p''{''q''}_''r''
, valign=top align=left, Same as or or
Same as
Same as
Same as or or
Same as
Same as
Same as or or
Same as
Same as
Same as
Same as

{, class=wikitable
!Space, , Group, , colspan=2, Apeirohedron, , Vertex, , colspan=2, Edge, , colspan=2, Face, , van Oss
apeirogon, , Notes

, - align=center BGCOLOR="#ffffe0"
, $\mathbb{C}^2$ , , ₂ sub>''r'' sub>2 , , ₂{4}_''r''{4}₂ , ,            
, , 2 , , , , {} , , 2 , , _p{4}_2', , ₂{4}_''r'', , align=left, Same as and , r=2,3,4,6

, - align=center BGCOLOR="#ffe0e0"
, $\mathbb{R}^2$, , ,4, {4,4}, , , , 2, , 4, , {}, , 2, , {4}, , {∞}, , align=left, Same as and
, - align=center BGCOLOR="#e0f0ff"
, $\mathbb{C}^2$
, valign=top, ₂ sub>3 sub>2
₂ sub>4 sub>2
₂ sub>6 sub>2
, valign=top, ₂{4}₃{4}_2
2{4}₄{4}_2
2{4}₆{4}₂
, valign=top,


, , 2 , , 9
16
36, , {} , , 2
, valign=top, ₂{4}_3
2{4}_4
2{4}₆ , , ₂{''q''}_''r''
, align=left, Same as and
Same as and
Same as and

{, class=wikitable
!Space, , Group, , colspan=2, Apeirohedron, , Vertex, , colspan=2, Edge, , colspan=2, Face, , van Oss
apeirogon, , Notes
, - align=center BGCOLOR="#ffe0e0"
, rowspan=2, $\mathbb{R}^2$
, rowspan=2, ₂ sub>2 sub>2
= ,3, , {3,6}, ,            
, , 1 , , 3 , , {} , , 2, , {3} , , {∞} , , align=left, Real triangular tiling
, - align=center BGCOLOR="#ffe0e0"
, {6,3} , , , , 2 , , 3, , {} , , 1, , {6} , , none , , align=left, Real hexagonal tiling
, - align=center BGCOLOR="#e0f0ff"
, rowspan=2, $\mathbb{C}^2$

, rowspan=2, ₃ sub>3 sub>3 , , ₃{3}₃{4}₃, , , , 1 , , 8, , ₃{} , , 3, , ₃{3}₃ , , ₃{4}₆ , , align=left, Same as
, - align=center BGCOLOR="#e0f0ff"
, ₃{4}₃{3}₃, , , , 3 , , 8, , ₃{} , , 2, , ₃{4}₃ , , ₃{12}₂ , ,

, - align=center BGCOLOR="#e0f0ff"
, $\mathbb{C}^2$
, , ₄ sub>4 sub>4 , , ₄{3}₄{3}₄, , , , 1 , , 6, , ₄{} , , 1, , ₄{3}₄ , , ₄{4}₄, , align=left, Self-dual, same as

, - align=center BGCOLOR="#e0f0ff"
, rowspan=2, $\mathbb{C}^2$
, rowspan=2, ₄ sub>4 sub>2 , , ₄{3}₄{4}₂, , , , 1 , , 12, , ₄{} , , 3, , ₄{3}₄ , , ₂{8}₄ , , align=left, Same as
, - align=center BGCOLOR="#e0f0ff"
, , ₂{4}₄{3}₄, , , , 3 , , 12, , {} , , 1, , ₂{4}₄ , , ₄{4}₄ , ,

Regular complex 3-apeirotopes

There are 16 regular complex apeirotopes in $\mathbb{C}^3$. Coxeter expresses 12 of them by δ where ''q'' is constrained to satisfy . These can also be decomposed as product apeirotopes: = . The first case is the $\mathbb{R}^3$ cubic honeycomb.

{, class=wikitable
, + Rank 4
!Space, , Group, , 3-apeirotope, , Vertex, , Edge, , Face, , Cell, , van Oss
apeirogon, , Notes
, - align=center BGCOLOR="#ffffe0"
, $\mathbb{C}^3$, , _''p'' sub>2 sub>2 sub>''r'', , δ = _''p''{4}₂{3}₂{4}_''r''
, , , , _''p''{} , , _''p''{4}₂ , , _''p''{4}₂{3}₂ , , _''p''{''q''}_''r'' , , align=left, Same as
, - align=center BGCOLOR="#ffe0e0"
, $\mathbb{R}^3$, , ₂ sub>2 sub>2 sub>2
= ,3,4, δ = ₂{4}₂{3}₂{4}₂
, , , , {}, , {4}, , {4,3} , , , , align=left, Cubic honeycomb
Same as or or
, - align=center BGCOLOR="#e0f0ff"
, rowspan=2, $\mathbb{C}^3$, , rowspan=2, ₃ sub>2 sub>2 sub>2, , δ = ₃{4}₂{3}₂{4}₂
, , , , ₃{} , , ₃{4}₂ , , ₃{4}₂{3}₂ , , , , align=left, Same as or or
, - align=center BGCOLOR="#e0f0ff"
, δ = ₂{4}₂{3}₂{4}₃
, , , , {}, , {4} , , {4,3} , , , , align=left, Same as
, - align=center BGCOLOR="#e0f0ff"
, $\mathbb{C}^3$, , ₃ sub>2 sub>2 sub>3, , δ = ₃{4}₂{3}₂{4}₃
, , , , ₃{} , , ₃{4}₂ , , ₃{4}₂{3}₂ , , , , align=left, Same as
, - align=center BGCOLOR="#e0f0ff"
, rowspan=2, $\mathbb{C}^3$, , rowspan=2, ₄ sub>2 sub>2 sub>2, , δ = ₄{4}₂{3}₂{4}₂
, , , , ₄{} , , ₄{4}₂ , , ₄{4}₂{3}₂ , , , , align=left, Same as or or
, - align=center BGCOLOR="#e0f0ff"
, δ = ₂{4}₂{3}₂{4}₄
, , , , {} , , {4} , , {4,3} , , , , align=left, Same as
, - align=center BGCOLOR="#e0f0ff"
, $\mathbb{C}^3$, , ₄ sub>2 sub>2 sub>4, , δ = ₄{4}₂{3}₂{4}₄
, , , , ₄{} , , ₄{4}₂ , , ₄{4}₂{3}₂ , , , , align=left, Same as
, - align=center BGCOLOR="#e0f0ff"
, rowspan=2, $\mathbb{C}^3$, , rowspan=2, ₆ sub>2 sub>2 sub>2, , δ = ₆{4}₂{3}₂{4}₂
, , , , ₆{} , , ₆{4}₂ , , ₆{4}₂{3}₂ , , , , align=left, Same as or or
, - align=center BGCOLOR="#e0f0ff"
, δ = ₂{4}₂{3}₂{4}₆
, , , , {} , , {4} , , {4,3} , , , , align=left, Same as
, - align=center BGCOLOR="#e0f0ff"
, rowspan=2, $\mathbb{C}^3$, , rowspan=2, ₆ sub>2 sub>2 sub>3, , δ = ₆{4}₂{3}₂{4}₃
, , , , ₆{} , , ₆{4}₂ , , ₆{4}₂{3}₂ , , , , align=left, Same as
, - align=center BGCOLOR="#e0f0ff"
, δ = ₃{4}₂{3}₂{4}₆
, , , , ₃{} , , ₃{4}₂ , , ₃{4}₂{3}₂ , , , , align=left, Same as
, - align=center BGCOLOR="#e0f0ff"
, $\mathbb{C}^3$, , ₆ sub>2 sub>2 sub>6, , δ = ₆{4}₂{3}₂{4}₆
, , , , ₆{} , , ₆{4}₂ , , ₆{4}₂{3}₂ , , , , align=left, Same as

{, class=wikitable
, + Rank 4, exceptional cases
!Space, , Group, , 3-apeirotope, , Vertex, , Edge, , Face, , Cell, , van Oss
apeirogon, , Notes
, - align=center BGCOLOR="#e0f0ff"
, rowspan=2, $\mathbb{C}^3$, , rowspan=2, ₂ sub>3 sub>3 sub>3 , , ₃{3}₃{3}₃{4}₂
, , 1 , , 24 ₃{} , , 27 ₃{3}₃ , , 2 ₃{3}₃{3}₃ , , ₃{4}₆ , , align=left, Same as
, - align=center BGCOLOR="#e0f0ff"
, ₂{4}₃{3}₃{3}₃
, , 2 , , 27 {} , , 24 ₂{4}₃ , , 1 ₂{4}₃{3}₃ , , ₂{12}₃, ,

, - align=center BGCOLOR="#e0f0ff"
, rowspan=2, $\mathbb{C}^3$, , rowspan=2, ₂ sub>2 sub>3 sub>3, , ₂{3}₂{4}₃{3}₃
, , 1, , 27 {}, , 72 ₂{3}₂, , 8 ₂{3}₂{4}₃ , , ₂{6}₆, ,
, - align=center BGCOLOR="#e0f0ff"
, , ₃{3}₃{4}₂{3}₂
, , 8, , 72 ₃{}, , 27 ₃{3}₃, , 1 ₃{3}₃{4}₂ , , ₃{6}₃, , align=left, Same as or

Regular complex 4-apeirotopes

There are 15 regular complex apeirotopes in $\mathbb{C}^4$. Coxeter expresses 12 of them by δ where ''q'' is constrained to satisfy . These can also be decomposed as product apeirotopes: = . The first case is the $\mathbb{R}^4$ tesseractic honeycomb. The 16-cell honeycomb and 24-cell honeycomb are real solutions. The last solution is generated has Witting polytope elements.

{, class=wikitable
, + Rank 5
!Space, , Group, , 4-apeirotope, , Vertex, , Edge, , Face, , Cell, , 4-face, , van Oss
apeirogon, , Notes

, - align=center BGCOLOR="#ffffe0"
, $\mathbb{C}^4$, , _''p'' sub>2 sub>2 sub>2 sub>''r'', , δ = _''p''{4}₂{3}₂{3}₂{4}_''r''
, , , , _''p''{}, , _''p''{4}₂, , _''p''{4}₂{3}₂ , , _''p''{4}₂{3}₂{3}₂ , , _''p''{''q''}_''r'' , , align=left, Same as
, - align=center BGCOLOR="#ffe0e0"
, $\mathbb{R}^4$, , ₂ sub>2 sub>2 sub>2 sub>2, , δ = {4,3,3,3}
, , , , {} , , {4} , , {4,3} , , {4,3,3} , , rowspan=3, {∞} , , align=left, Tesseractic honeycomb
Same as

, - align=center BGCOLOR="#ffe0e0"
, rowspan=2, $\mathbb{R}^4$, , rowspan=2, ₂ sub>2 sub>2 sub>2 sub>2
= ,4,3,3, , {3,3,4,3}
, , 1 , , 12 {} , , 32 {3} , , 24 {3,3} , , 3 {3,3,4} , , align=left, Real 16-cell honeycomb
Same as
, - align=center BGCOLOR="#ffe0e0"
, {3,4,3,3}
, , 3 , , 24 {} , , 32 {3} , , 12 {3,4} , , 1 {3,4,3} , , align=left, Real 24-cell honeycomb
Same as or

, - align=center BGCOLOR="#e0f0ff"
, $\mathbb{C}^4$, , ₃ sub>3 sub>3 sub>3 sub>3 , , ₃{3}₃{3}₃{3}₃{3}₃
, , 1 , , 80 ₃{} , , 270 ₃{3}₃ , , 80 ₃{3}₃{3}₃ , , 1 ₃{3}₃{3}₃{3}₃ , , ₃{4}₆ , , align=left, $\mathbb{R}^8$ representation 5₂₁

Regular complex 5-apeirotopes and higher

There are only 12 regular complex apeirotopes in $\mathbb{C}^5$ or higher, expressed δ where ''q'' is constrained to satisfy . These can also be decomposed a product of ''n'' apeirogons: ... = ... . The first case is the real $\mathbb{R}^n$ hypercube honeycomb.
{, class=wikitable
, + Rank 6
!Space, , Group, , 5-apeirotopes, , Vertices, , Edge, , Face, , Cell, , 4-face, , 5-face, , van Oss
apeirogon, , Notes
, - align=center BGCOLOR="#ffffe0"
, $\mathbb{C}^5$, , _''p'' sub>2 sub>2 sub>2 sub>2 sub>''r'', , δ = _''p''{4}₂{3}₂{3}₂{3}₂{4}_''r''
, , , , _''p''{} , , _''p''{4}₂ , , _''p''{4}₂{3}₂ , , _''p''{4}₂{3}₂{3}₂ , , _''p''{4}₂{3}₂{3}₂{3}₂ , , _''p''{''q''}_''r'', , Same as
, - align=center BGCOLOR="#ffe0e0"
, $\mathbb{R}^5$, , ₂ sub>2 sub>2 sub>2 sub>2 sub>2
= ,3,3,3,4, δ = {4,3,3,3,4}
, , , , {} , , {4} , , {4,3} , , {4,3,3} , , {4,3,3,3} , , {∞}, , 5-cubic honeycomb
Same as

van Oss polygon

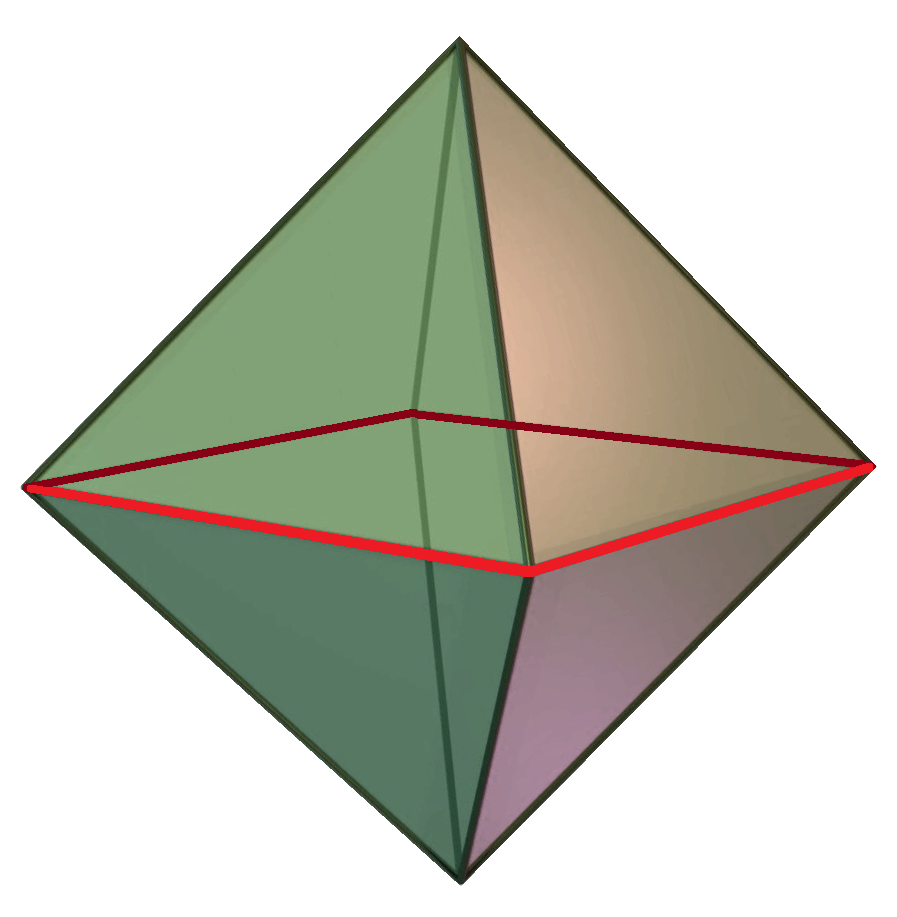A van Oss polygon is a regular polygon in the plane (real plane $\mathbb{R}^2$, or unitary plane $\mathbb{C}^2$) in which both an edge and the centroid of a regular polytope lie, and formed of elements of the polytope. Not all regular polytopes have Van Oss polygons.

For example, the van Oss polygons of a real octahedron are the three squares whose planes pass through its center. In contrast a cube does not have a van Oss polygon because the edge-to-center plane cuts diagonally across two square faces and the two edges of the cube which lie in the plane do not form a polygon.

Infinite honeycombs also have van Oss apeirogons. For example, the real square tiling and triangular tiling have apeirogons {∞} van Oss apeirogons.

If it exists, the ''van Oss polygon'' of regular complex polytope of the form _''p''{''q''}_''r''{''s''}_''t''... has ''p''-edges.

Non-regular complex polytopes

Product complex polytopes

{, class=wikitable align=right width=360
, + Example product complex polytope
, - valign=top
,
Complex product polygon or {}×₅{} has 10 vertices connected by 5 2-edges and 2 5-edges, with its real representation as a 3-dimensional pentagonal prism.
, width=200,
The dual polygon,{}+₅{} has 7 vertices centered on the edges of the original, connected by 10 edges. Its real representation is a pentagonal bipyramid.

Some complex polytopes can be represented as Cartesian products. These product polytopes are not strictly regular since they'll have more than one facet type, but some can represent lower symmetry of regular forms if all the orthogonal polytopes are identical. For example, the product _''p''{}×_''p''{} or of two 1-dimensional polytopes is the same as the regular _''p''{4}₂ or . More general products, like _''p''{}×_''q''{} have real representations as the 4-dimensional ''p''-''q'' duoprisms. The dual of a product polytope can be written as a sum _''p''{}+_''q''{} and have real representations as the 4-dimensional ''p''-''q'' duopyramid. The _''p''{}+_''p''{} can have its symmetry doubled as a regular complex polytope ₂{4}_''p'' or .

Similarly, a $\mathbb{C}^3$ complex polyhedron can be constructed as a triple product: _''p''{}×_''p''{}×_''p''{} or is the same as the regular ''generalized cube'', _''p''{4}₂{3}₂ or , as well as product _''p''{4}₂×_''p''{} or .

Quasiregular polygons

A quasiregular polygon is a truncation of a regular polygon. A quasiregular polygon contains alternate edges of the regular polygons and . The quasiregular polygon has ''p'' vertices on the p-edges of the regular form.

{, class=wikitable
, + Example quasiregular polygons
!_''p'' 'q''sub>''r'' , , ₂ sub>2, , ₃ sub>2, , ₄ sub>2, , ₅ sub>2, , ₆ sub>2, , ₇ sub>2, , ₈ sub>2 , , ₃ sub>3 , , ₃ sub>3
, - align=center
!Regular

,

4 2-edges
,

9 3-edges
,

16 4-edges
,

25 5-edges
,

36 6-edges
,

49 8-edges
,

64 8-edges
,

,

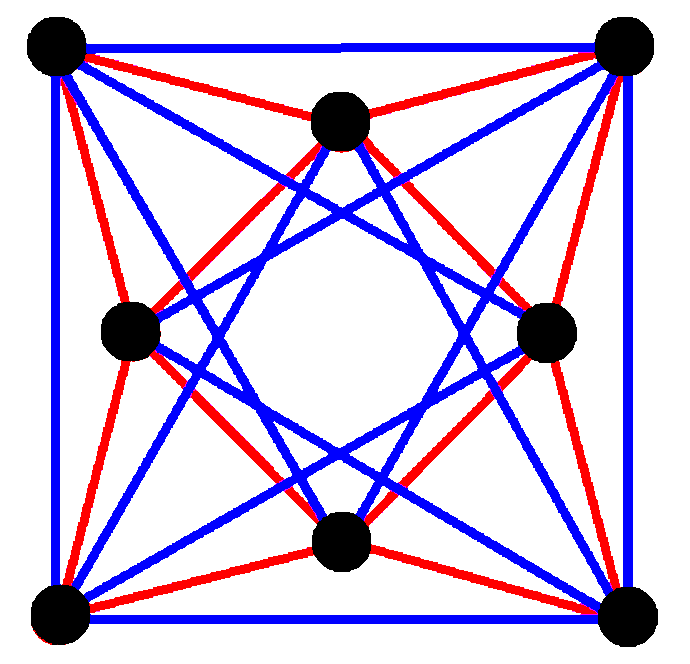
, - align=center
!Quasiregular

,
=
4+4 2-edges
,

6 2-edges
9 3-edges
,

8 2-edges
16 4-edges
,

10 2-edges
25 5-edges
,

12 2-edges
36 6-edges
,

14 2-edges
49 7-edges
,

16 2-edges
64 8-edges
,
=
,
=
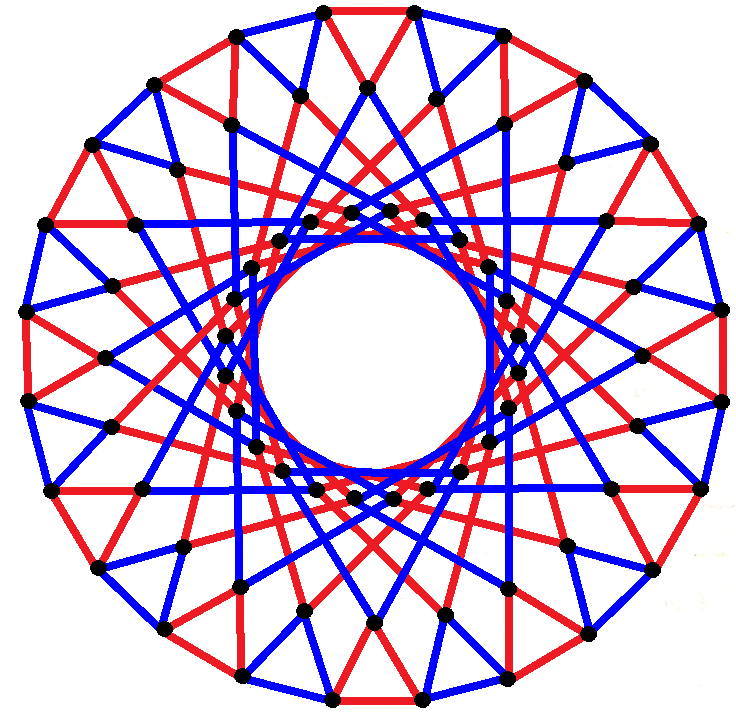
, - align=center
!Regular

,

4 2-edges
,

6 2-edges
,

8 2-edges
,

10 2-edges
,

12 2-edges
,

14 2-edges
,

16 2-edges
,

,

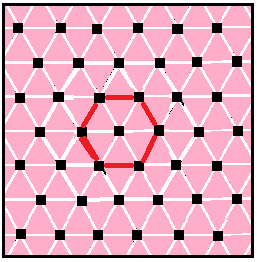
Quasiregular apeirogons

There are 7 quasiregular complex apeirogons which alternate edges of a regular apeirogon and its regular dual. The vertex arrangements of these apeirogon have real representations with the regular and uniform tilings of the Euclidean plane. The last column for the 6{3}6 apeirogon is not only self-dual, but the dual coincides with itself with overlapping hexagonal edges, thus their quasiregular form also has overlapping hexagonal edges, so it can't be drawn with two alternating colors like the others. The symmetry of the self-dual families can be doubled, so creating an identical geometry as the regular forms: =

{, class=wikitable
!_''p'' 'q''sub>''r'' , , ₄ sub>2, , ₄ sub>4 , , ₆ sub>2 , , ₆ sub>3 , , ₃ 2sub>2, , ₃ sub>3 , , ₆ sub>6
, - align=center
!Regular
or _''p''{''q''}_''r''
, ,

, ,

, ,

, ,

, ,

, ,

, ,

, - align=center
!Quasiregular

, ,

, ,
=
, ,

, ,

, ,

, ,
=
, ,
=

, - align=center
!Regular dual
or _''r''{''q''}_''p''
, ,

, ,

, ,

, ,

, ,

, ,

, ,

Quasiregular polyhedra

Like real polytopes, a complex quasiregular polyhedron can be constructed as a rectification (a complete truncation) of a regular polyhedron. Vertices are created mid-edge of the regular polyhedron and faces of the regular polyhedron and its dual are positioned alternating across common edges.

For example, a p-generalized cube, , has ''p''³ vertices, 3''p''² edges, and 3''p'' ''p''-generalized square faces, while the ''p''-generalized octahedron, , has 3''p'' vertices, 3''p''² edges and ''p''³ triangular faces. The middle quasiregular form ''p''-generalized cuboctahedron, , has 3''p''² vertices, 3''p''³ edges, and 3''p''+''p''³ faces.

Also the rectification of the Hessian polyhedron , is , a quasiregular form sharing the geometry of the regular complex polyhedron .

{, class=wikitable width=750
, + Quasiregular examples
!colspan=6, Generalized cube/octahedra , , rowspan=2, Hessian polyhedron
, - align=center
! , , p=2 (real), , p=3 , , p=4 , , p=5 , , p=6
, - align=center valign=top
!Generalized
cubes

(regular)
, BGCOLOR="#ffe0e0",
Cube
, 8 vertices, 12 2-edges, and 6 faces.
,
, 27 vertices, 27 3-edges, and 9 faces, with one face blue and red
,
, 64 vertices, 48 4-edges, and 12 faces.
,
, 125 vertices, 75 5-edges, and 15 faces.
,
, 216 vertices, 108 6-edges, and 18 faces.
, BGCOLOR="#ffffe0",
, 27 vertices, 72 6-edges, and 27 faces.
, - align=center valign=top
!Generalized
cuboctahedra

(quasiregular)
, BGCOLOR="#ffe0e0",
Cuboctahedron
, 12 vertices, 24 2-edges, and 6+8 faces.
,
, 27 vertices, 81 2-edges, and 9+27 faces, with one face blue
,
, 48 vertices, 192 2-edges, and 12+64 faces, with one face blue
,
, 75 vertices, 375 2-edges, and 15+125 faces.
,
, 108 vertices, 648 2-edges, and 18+216 faces.
, BGCOLOR="#ffffe0",
= , 72 vertices, 216 3-edges, and 54 faces.
, - align=center valign=top
!Generalized
octahedra

(regular)
, BGCOLOR="#ffe0e0",
Octahedron
, 6 vertices, 12 2-edges, and 8 {3} faces.
,
, 9 vertices, 27 2-edges, and 27 {3} faces.
,
, 12 vertices, 48 2-edges, and 64 {3} faces.
,
, 15 vertices, 75 2-edges, and 125 {3} faces.
,
, 18 vertices, 108 2-edges, and 216 {3} faces.
, BGCOLOR="#ffffe0",
, 27 vertices, 72 6-edges, and 27 faces.

Other complex polytopes with unitary reflections of period two

Other nonregular complex polytopes can be constructed within unitary reflection groups that don't make linear Coxeter graphs. In Coxeter diagrams with loops Coxeter marks a special period interior, like or symbol (1₁ 1 1)³, and group 1 1sup>3. These complex polytopes have not been systematically explored beyond a few cases.

The group is defined by 3 unitary reflections, R₁, R₂, R₃, all order 2: R₁² = R₁² = R₃² = (R₁R₂)³ = (R₂R₃)³ = (R₃R₁)³ = (R₁R₂R₃R₁)^''p'' = 1. The period ''p'' can be seen as a double rotation in real $\mathbb{R}^4$.

As with all Wythoff constructions, polytopes generated by reflections, the number of vertices of a single-ringed Coxeter diagram polytope is equal to the order of the group divided by the order of the subgroup where the ringed node is removed. For example, a real cube has Coxeter diagram , with octahedral symmetry order 48, and subgroup dihedral symmetry order 6, so the number of vertices of a cube is 48/6=8. Facets are constructed by removing one node furthest from the ringed node, for example for the cube. Vertex figures are generated by removing a ringed node and ringing one or more connected nodes, and for the cube.

Coxeter represents these groups by the following symbols. Some groups have the same order, but a different structure, defining the same vertex arrangement in complex polytopes, but different edges and higher elements, like and with ''p''≠3.

{, class=wikitable
, + Groups generated by unitary reflections
!Coxeter diagram, , Order, , Symbol or Position in Table VII of Shephard and Todd (1954)
, -
, , ( and ), , ...

, , ''p''^{''n'' − 1} ''n''!, ''p'' ≥ 3 , , ''G''(''p'', ''p'', ''n''), 'p'' 1 1sup>''p'', 1 (''n''−2)^''p''sup>3
, -
, , , , 72·6!, 108·9! , , Nos. 33, 34, 2 2sup>3, 2 3sup>3
, -
, , ( and ), ( and ) , , 14·4!, 3·6!, 64·5! , , Nos. 24, 27, 29

Coxeter calls some of these complex polyhedra ''almost regular'' because they have regular facets and vertex figures. The first is a lower symmetry form of the generalized cross-polytope in $\mathbb{C}^3$. The second is a fractional generalized cube, reducing ''p''-edges into single vertices leaving ordinary 2-edges. Three of them are related to the finite regular skew polyhedron in $\mathbb{R}^4$.
{, class="wikitable sortable"
, + Some almost regular complex polyhedraCoxeter, Groups generated by Unitary Reflections of Period Two (1956), Table III: Some Complex Polytopes, p.413
!Space, , Group, , Order, , Coxeter
symbols, , Vertices, , Edges, , Faces, , Vertex
figure, , Notes
, - align=center BGCOLOR="#ffffe0"
, rowspan=2, $\mathbb{C}^3$, , rowspan=2, 1 1^''p''sup>3

''p''=2,3,4..., , rowspan=2, 6''p''² , , (1 1 1₁^''p'')³
, , 3''p'', , 3''p''² , , {3} , , {2''p''}, , align=left, Shephard symbol (1 1; 1₁)^''p''
same as β =
, - align=center BGCOLOR="#ffffe0"
, (1₁ 1 1^''p'')³
, , ''p''², , , , {3} , , {6}, , align=left, Shephard symbol (1₁ 1; 1)^''p''
1/''p'' γ

, - align=center BGCOLOR="#ffe0e0"
, rowspan=2, $\mathbb{R}^3$, , rowspan=2, 1 1²sup>3
, , rowspan=2, 24 , , (1 1 1₁²)³
, , 6, , 12 , , 8 {3} , , {4}, , align=left, Same as β = = real octahedron
, - align=center BGCOLOR="#ffe0e0"
, (1₁ 1 1²)³
, , 4, , 6 , , 4 {3} , , {3}, , align=left, 1/2 γ = = α₃ = real tetrahedron

, - align=center BGCOLOR="#e0ffff"
, rowspan=2, $\mathbb{C}^3$, , rowspan=2, 1 1sup>3
, , rowspan=2, 54 , , (1 1 1₁)³
, , 9, , 27 , , {3} , , {6}, , align=left, Shephard symbol (1 1; 1₁)³
same as β =
, - align=center BGCOLOR="#e0ffff"
, (1₁ 1 1)³
, , 9, , 27 , , {3} , , {6}, , align=left, Shephard symbol (1₁ 1; 1)³
1/3 γ = β
, - align=center BGCOLOR="#e0ffff"
, rowspan=2, $\mathbb{C}^3$, , rowspan=2, 1 1⁴sup>3
, , rowspan=2, 96 , , (1 1 1₁⁴)³
, , 12, , 48 , , {3} , , {8}, , align=left, Shephard symbol (1 1; 1₁)⁴
same as β =
, - align=center BGCOLOR="#e0ffff"
, (1₁ 1 1⁴)³
, , 16, , , , {3} , , {6}, , align=left, Shephard symbol (1₁ 1; 1)⁴
1/4 γ
, - align=center BGCOLOR="#e0ffff"
, rowspan=2, $\mathbb{C}^3$, , rowspan=2, 1 1⁵sup>3
, , rowspan=2, 150 , , (1 1 1₁⁵)³
, , 15, , 75 , , {3} , , {10}, , align=left, Shephard symbol (1 1; 1₁)⁵
same as β =
, - align=center BGCOLOR="#e0ffff"
, (1₁ 1 1⁵)³
, , 25 , , , , {3} , , {6}, , align=left, Shephard symbol (1₁ 1; 1)⁵
1/5 γ
, - align=center BGCOLOR="#e0ffff"
, rowspan=2, $\mathbb{C}^3$, , rowspan=2, 1 1⁶sup>3
, , rowspan=2, 216 , , (1 1 1₁⁶)³
, , 18, , 216 , , {3} , , {12}, , align=left, Shephard symbol (1 1; 1₁)⁶
same as β =
, - align=center BGCOLOR="#e0ffff"
, (1₁ 1 1⁶)³
, , 36 , , , , {3} , , {6}, , align=left, Shephard symbol (1₁ 1; 1)⁶
1/6 γ

, - align=center BGCOLOR="#e0f0ff"
, rowspan=2, $\mathbb{C}^3$, , rowspan=2, 1 1⁴sup>4
, , rowspan=2, 336 , , (1 1 1₁⁴)⁴
, , 42, , 168 , , 112 {3} , , {8}, , align=left, $\mathbb{R}^4$ representation {3,8|,4} = {3,8}₈
, - align=center BGCOLOR="#e0f0ff"
, (1₁ 1 1⁴)⁴
, , 56 , , , , {3} , , {6}, ,

, - align=center BGCOLOR="#e0f0ff"
, rowspan=2, $\mathbb{C}^3$, , rowspan=2, 1 1⁵sup>4
, , rowspan=4, 2160 , , (1 1 1₁⁵)⁴
, , 216 , , 1080 , , 720 {3} , , {10}, , align=left, $\mathbb{R}^4$ representation {3,10|,4} = {3,10}₈
, - align=center BGCOLOR="#e0f0ff"
, (1₁ 1 1⁵)⁴
, , 360, , , , {3} , , {6}, , align=left,

, - align=center BGCOLOR="#e0f0ff"
, rowspan=2, $\mathbb{C}^3$, , rowspan=2, 1 1⁴sup>5
, , (1 1 1₁⁴)⁵
, , 270, , 1080 , , 720 {3} , , {8}, , align=left, $\mathbb{R}^4$ representation {3,8|,5} = {3,8}₁₀
, - align=center BGCOLOR="#e0f0ff"
, (1₁ 1 1⁴)⁵
, , 360, , , , {3} , , {6}, ,

Coxeter defines other groups with anti-unitary constructions, for example these three. The first was discovered and drawn by Peter McMullen in 1966.
{, class="wikitable sortable"
, + More almost regular complex polyhedra
!Space, , Group, , Order, , Coxeter
symbols, , Vertices, , Edges, , Faces, , Vertex
figure, , Notes
, - align=center BGCOLOR="#e0f0ff"
, $\mathbb{C}^3$, , 1⁴ 1⁴sup>(3)
, , 336 , , (1₁ 1⁴ 1⁴)⁽³⁾
, , 56 , , 168 , , 84 {4} , , {6}, , align=left, $\mathbb{R}^4$ representation {4,6|,3} = {4,6}₆
, - align=center BGCOLOR="#e0f0ff"
, $\mathbb{C}^3$, , ⁵ 1⁴ 1⁴sup>(3)
, , rowspan=2, 2160 , , (1₁⁵ 1⁴ 1⁴)⁽³⁾
, , 216 , , 1080 , , 540 {4} , , {10}, , align=left, $\mathbb{R}^4$ representation {4,10|,3} = {4,10}₆
, - align=center BGCOLOR="#e0f0ff"
, $\mathbb{C}^3$, , ⁴ 1⁵ 1⁵sup>(3)
, , (1₁⁴ 1⁵ 1⁵)⁽³⁾
, , 270 , , 1080 , , 432 {5} , , {8}, , align=left, $\mathbb{R}^4$ representation {5,8|,3} = {5,8}₆

{, class="wikitable sortable"
, + Some complex 4-polytopes
!Space, , Group, , Order, , Coxeter
symbols, , Vertices, , Other
elements, , Cells, , Vertex
figure, , Notes

, - align=center BGCOLOR="#ffffe0"
, rowspan=2, $\mathbb{C}^4$, , rowspan=2, 1 2^''p''sup>3

''p''=2,3,4..., , rowspan=2, 24''p''³ , , (1 1 2₂^p)³
, , 4''p'' , , , , , , , , align=left, Shephard (2₂ 1; 1)^''p''
same as β =
, - align=center BGCOLOR="#ffffe0"
, (1₁ 1 2^''p'' )³
, , ''p''³ , , , ,
, , , , align=left, Shephard (2 1; 1₁)^''p''
1/''p'' γ

, - align=center BGCOLOR="#ffe0e0"
, rowspan=2, $\mathbb{R}^4$, , rowspan=2, 1 2²sup>3
= ^1,1,1BR>, , rowspan=2, 192 , , (1 1 2₂²)³
, , rowspan=2, 8 , , rowspan=2, 24 edges
32 faces , , rowspan=2, 16 , , rowspan=2, , , align=left, β = , real 16-cell
, - align=center BGCOLOR="#ffe0e0"
, (1₁ 1 2² )³
, , align=left, 1/2 γ = = β, real 16-cell

, - align=center BGCOLOR="#e0ffff"
, rowspan=2, $\mathbb{C}^4$, , rowspan=2, 1 2sup>3
, , rowspan=2, 648 , , (1 1 2₂)³
, , 12 , , , , , , , , align=left, Shephard (2₂ 1; 1)³
same as β =
, - align=center BGCOLOR="#e0ffff"
, (1₁ 1 2³)³
, , 27 , , , ,
, , , , align=left, Shephard (2 1; 1₁)³
1/3 γ

, - align=center BGCOLOR="#e0ffff"
, rowspan=2, $\mathbb{C}^4$, , rowspan=2, 1 2⁴sup>3
, , rowspan=2, 1536 , , (1 1 2₂⁴)³
, , 16 , , , , , , , , align=left, Shephard (2₂ 1; 1)⁴
same as β =
, - align=center BGCOLOR="#e0ffff"
, (1₁ 1 2⁴ )³
, , 64 , , , ,
, , , , align=left, Shephard (2 1; 1₁)⁴
1/4 γ

, - align=center BGCOLOR="#e0f0ff"
, rowspan=3, $\mathbb{C}^4$, , rowspan=3, ⁴ 1 2sup>3
, , rowspan=5, 7680 , , (2₂ 1⁴ 1)³
, , 80, , , , , , , , align=left, Shephard (2₂ 1; 1)⁴
, - align=center BGCOLOR="#e0f0ff"
, (1₁⁴ 1 2)³
, , 160, , , ,
, , , , align=left, Shephard (2 1; 1₁)⁴
, - align=center BGCOLOR="#e0f0ff"
, (1₁ 1⁴ 2)³
, , 320 , , , ,
, , , , align=left, Shephard (2 1₁; 1)⁴

, - align=center BGCOLOR="#e0f0ff"
, rowspan=2, $\mathbb{C}^4$, , rowspan=2, 1 2sup>4
, , (1 1 2₂)⁴
, , 80, , 640 edges
1280 triangles , , 640 , , , , align=left,
, - align=center BGCOLOR="#e0f0ff"
, (1₁ 1 2)⁴
, , 320, , , ,
, , , , align=left,

{, class="wikitable sortable"
, + Some complex 5-polytopes
!Space, , Group, , Order, , Coxeter
symbols, , Vertices, , Edges, , Facets, , Vertex
figure, , Notes

, - align=center BGCOLOR="#ffffe0"
, rowspan=2, $\mathbb{C}^5$, , rowspan=2, 1 3^''p''sup>3

''p''=2,3,4..., , rowspan=2, 120''p''⁴ , , (1 1 3₃^p)³
, , 5''p'' , , , , , , , , align=left, Shephard (3₃ 1; 1)^''p''
same as β =
, - align=center BGCOLOR="#ffffe0"
, (1₁ 1 3^''p'')³
, , ''p''⁴ , , , ,
, , , , align=left, Shephard (3 1; 1₁)^''p''
1/''p'' γ

, - align=center BGCOLOR="#e0f0ff"
, rowspan=2, $\mathbb{C}^5$, , rowspan=2, 2 1sup>3
, , rowspan=2, 51840 , , (2 1 2₂)³
, , 80, , , ,
, , , , align=left, Shephard (2 1; 2₂)³
, - align=center BGCOLOR="#e0f0ff"
, (2 1₁ 2)³
, , 432, , , , , , , , align=left, Shephard (2 1₁; 2)³

{, class="wikitable sortable"
, + Some complex 6-polytopes
!Space, , Group, , Order, , Coxeter
symbols, , Vertices, , Edges, , Facets, , Vertex
figure, , Notes

, - align=center BGCOLOR="#ffffe0"
, rowspan=2, $\mathbb{C}^6$, , rowspan=2, 1 4^''p''sup>3

''p''=2,3,4..., , rowspan=2, 720''p''⁵ , , (1 1 4₄^''p'')³
, , 6''p'' , , , , , , , , align=left, Shephard (4₄ 1; 1)^''p''
same as β =
, - align=center BGCOLOR="#ffffe0"
, (1₁ 1 4^''p'')³
, , ''p''⁵ , , , ,
, , , , align=left, Shephard (4 1; 1₁)^''p''
1/''p'' γ

, - align=center BGCOLOR="#e0f0ff"
, rowspan=3, $\mathbb{C}^6$, , rowspan=3, 2 3sup>3
, , rowspan=3, 39191040 , , (2 1 3₃)³
, , 756, , , ,
, , , , align=left, Shephard (2 1; 3₃)³
, - align=center BGCOLOR="#e0f0ff"
, (2₂ 1 3)³
, , 4032, , , ,
, , , , align=left, Shephard (2₂ 1; 3)³
, - align=center BGCOLOR="#e0f0ff"
, (2 1₁ 3)³
, , 54432, , , ,
, , , , align=left, Shephard (2 1₁; 3)³

Visualizations

Complex_polyhedron_almost_regular_42_vertices.png, (1 1 1₁⁴)⁴, has 42 vertices, 168 edges and 112 triangular faces, seen in this 14-gonal projection.
Complex polyhedron almost regular 46 vertices.png, (1⁴ 1⁴ 1₁)⁽³⁾, has 56 vertices, 168 edges and 84 square faces, seen in this 14-gonal projection.
Complex_4-polytope_almost_regular_80_vertices.png, (1 1 2₂)⁴, has 80 vertices, 640 edges, 1280 triangular faces and 640 tetrahedral cells, seen in this 20-gonal projection.Coxeter, Complex Regular Polytopes, pp.172-173

See also

* Quaternionic polytope

Notes

References

* Coxeter, H. S. M. and Moser, W. O. J.; ''Generators and Relations for Discrete Groups'' (1965), esp pp 67–80.
*
* Coxeter, H. S. M. and Shephard, G.C.; Portraits of a family of complex polytopes, ''Leonardo'' Vol 25, No 3/4, (1992), pp 239–244,
* Shephard, G.C.; ''Regular complex polytopes'', ''Proc. London math. Soc.'' Series 3, Vol 2, (1952), pp 82–97.
* G. C. Shephard, J. A. Todd, ''Finite unitary reflection groups'', Canadian Journal of Mathematics. 6(1954), 274-30

* Gustav I. Lehrer and Donald E. Taylor, ''Unitary Reflection Groups'', Cambridge University Press 2009

Further reading

* F. Arthur Sherk, Peter McMullen, Anthony C. Thompson and Asia Ivić Weiss, editors: ''Kaleidoscopes — Selected Writings of H.S.M. Coxeter.'', Paper 25, ''Finite groups generated by unitary reflections'', p 415-425, John Wiley, 1995,
* {{citation , last1 = McMullen , first1 = Peter , author1-link = Peter McMullen , first2 = Egon , last2 = Schulte , title = Abstract Regular Polytopes , edition = 1st , publisher = Cambridge University Press , isbn = 0-521-81496-0 , date = December 2002 , url-access = registration , url = https://archive.org/details/abstractregularp0000mcmu Chapter 9 ''Unitary Groups and Hermitian Forms'', pp. 289–298

Polytopes
Complex analysis