Clebsch–Gordan Coefficients For SU(3) on:
[Wikipedia]
[Google]
[Amazon]
In mathematical physics,
 A slightly differently normalized standard basis consists of the ''F-spin'' operators, which are defined as for the 3, and are utilized to apply to ''any representation of this algebra''.
The Cartan–Weyl basis of the Lie algebra of is obtained by another change of basis, where one defines,
:
:
:
:
:
Because of the factors of ''i'' in these formulas, this is technically a basis for the complexification of the su(3) Lie algebra, namely sl(3,C). The preceding basis is then essentially the same one used in Hall's book.
A slightly differently normalized standard basis consists of the ''F-spin'' operators, which are defined as for the 3, and are utilized to apply to ''any representation of this algebra''.
The Cartan–Weyl basis of the Lie algebra of is obtained by another change of basis, where one defines,
:
:
:
:
:
Because of the factors of ''i'' in these formulas, this is technically a basis for the complexification of the su(3) Lie algebra, namely sl(3,C). The preceding basis is then essentially the same one used in Hall's book.
 :
their irreducible characters are given by Note: There is a typo in the final quoting of the result - in Equation 10.121 the first should instead be a .
:
and the corresponding Haar measure is
such that and ,
An multiplet may be completely specified by five labels, two of which, the eigenvalues of the two Casimirs, are common to all members of the multiplet. This generalizes the mere two labels for multiplets, namely the eigenvalues of its quadratic Casimir and of 3.
Since , we can
label different states by the eigenvalues of and operators, , for a given eigenvalue of the isospin Casimir. The action of operators on this states are,
:
their irreducible characters are given by Note: There is a typo in the final quoting of the result - in Equation 10.121 the first should instead be a .
:
and the corresponding Haar measure is
such that and ,
An multiplet may be completely specified by five labels, two of which, the eigenvalues of the two Casimirs, are common to all members of the multiplet. This generalizes the mere two labels for multiplets, namely the eigenvalues of its quadratic Casimir and of 3.
Since , we can
label different states by the eigenvalues of and operators, , for a given eigenvalue of the isospin Casimir. The action of operators on this states are,Senner & Schulten
/ref> :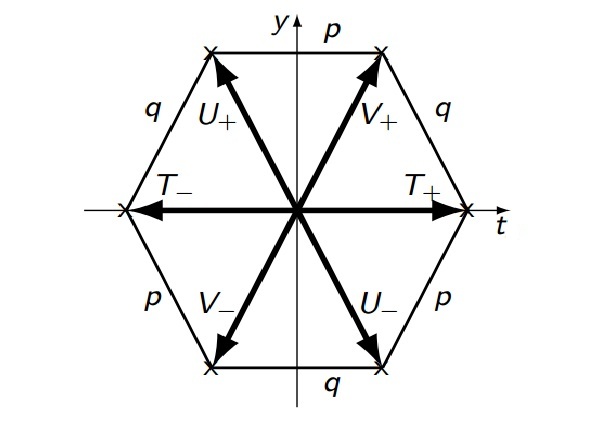 :
:
:
:
:
:
Here,
:
and
:
All the other states of the representation can be constructed by the successive application of the
:
:
:
:
:
:
Here,
:
and
:
All the other states of the representation can be constructed by the successive application of the
Since the Clebsch–Gordan coefficients are all real, the following symmetry property can be deduced, : Where .
Clebsch–Gordan coefficients
In physics, the Clebsch–Gordan (CG) coefficients are numbers that arise in angular momentum coupling in quantum mechanics. They appear as the expansion coefficients of total angular momentum eigenstates in an uncoupled tensor product basis. In ...
are the expansion coefficients of total angular momentum eigenstate
In quantum physics, a quantum state is a mathematical entity that provides a probability distribution for the outcomes of each possible measurement on a system. Knowledge of the quantum state together with the rules for the system's evolution in t ...
s in an uncoupled tensor product basis. Mathematically, they specify the decomposition of the tensor product of two irreducible representations into a direct sum
The direct sum is an operation between structures in abstract algebra, a branch of mathematics. It is defined differently, but analogously, for different kinds of structures. To see how the direct sum is used in abstract algebra, consider a more ...
of irreducible representations, where the type and the multiplicities of these irreducible representations are known abstractly. The name derives from the German mathematicians Alfred Clebsch (1833–1872) and Paul Gordan (1837–1912), who encountered an equivalent problem in invariant theory.
Generalization to SU(3) of Clebsch–Gordan coefficients is useful because of their utility in characterizing hadronic decays, where a flavor-SU(3) symmetry exists (the '' eightfold way'') that connects the three light quarks
A quark () is a type of elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. All commonly o ...
: up, down, and strange.
The SU(3) group
Thespecial unitary group
In mathematics, the special unitary group of degree , denoted , is the Lie group of unitary matrices with determinant 1.
The more general unitary matrices may have complex determinants with absolute value 1, rather than real 1 in the special ...
''SU'' is the group of unitary matrices whose determinant is equal to 1. This set is closed under matrix multiplication. All transformations characterized by the special unitary group leave norms unchanged. The symmetry appears in quantum chromodynamics
In theoretical physics, quantum chromodynamics (QCD) is the theory of the strong interaction between quarks mediated by gluons. Quarks are fundamental particles that make up composite hadrons such as the proton, neutron and pion. QCD is a type o ...
, and, as already indicated in the light quark flavour symmetry dubbed the Eightfold Way (physics). The quarks possess colour quantum numbers and form the fundamental (triplet) representation of an group.
The group is a subgroup of group , the group of all 3×3 unitary matrices. The unitarity condition imposes nine constraint relations on the total 18 degrees of freedom of a 3×3 complex matrix. Thus, the dimension of the group is 9. Furthermore, multiplying a ''U'' by a phase, leaves the norm invariant. Thus can be decomposed into a direct product . Because of this additional constraint, has dimension 8.
Generators of the Lie algebra
Every unitary matrix can be written in the form : where ''H'' is hermitian. The elements of can be expressed as : where are the 8 linearly independent matrices forming the basis of the Lie algebra of , in the triplet representation. The unit determinant condition requires the matrices to be traceless, since : . An explicit basis in the fundamental, 3, representation can be constructed in analogy to the Pauli matrix algebra of the spin operators. It consists of the Gell-Mann matrices, : These are the generators of the group in the triplet representation, and they are normalized as : The Lie algebra structure constants of the group are given by the commutators of : where are the structure constants completely antisymmetric and are analogous to the Levi-Civita symbol of . In general, they vanish, unless they contain an odd number of indices from the set , corresponding to the antisymmetric s. Note . Moreover, : where are the completely symmetric coefficient constants. They vanish if the number of indices from the set is odd. In terms of the matrices, :Standard basis
 A slightly differently normalized standard basis consists of the ''F-spin'' operators, which are defined as for the 3, and are utilized to apply to ''any representation of this algebra''.
The Cartan–Weyl basis of the Lie algebra of is obtained by another change of basis, where one defines,
:
:
:
:
:
Because of the factors of ''i'' in these formulas, this is technically a basis for the complexification of the su(3) Lie algebra, namely sl(3,C). The preceding basis is then essentially the same one used in Hall's book.
A slightly differently normalized standard basis consists of the ''F-spin'' operators, which are defined as for the 3, and are utilized to apply to ''any representation of this algebra''.
The Cartan–Weyl basis of the Lie algebra of is obtained by another change of basis, where one defines,
:
:
:
:
:
Because of the factors of ''i'' in these formulas, this is technically a basis for the complexification of the su(3) Lie algebra, namely sl(3,C). The preceding basis is then essentially the same one used in Hall's book.
Commutation algebra of the generators
The standard form of generators of the group satisfies the commutation relations given below, : : : : : : : : : : : : : : : : All other commutation relations follow from hermitian conjugation of these operators. These commutation relations can be used to construct the irreducible representations of the group. The representations of the group lie in the 2-dimensional plane. Here, stands for the z-component of Isospin and is theHypercharge
In particle physics, the hypercharge (a portmanteau of hyperonic and charge) ''Y'' of a particle is a quantum number conserved under the strong interaction. The concept of hypercharge provides a single charge operator that accounts for propert ...
, and they comprise the (abelian) Cartan subalgebra
In mathematics, a Cartan subalgebra, often abbreviated as CSA, is a nilpotent subalgebra \mathfrak of a Lie algebra \mathfrak that is self-normalising (if ,Y\in \mathfrak for all X \in \mathfrak, then Y \in \mathfrak). They were introduced by ...
of the full Lie algebra. The maximum number of mutually commuting generators of a Lie algebra is called its ''rank'': has rank 2. The remaining 6 generators, the ± ladder operators, correspond to the 6 roots
A root is the part of a plant, generally underground, that anchors the plant body, and absorbs and stores water and nutrients.
Root or roots may also refer to:
Art, entertainment, and media
* ''The Root'' (magazine), an online magazine focusing ...
arranged on the 2-dimensional hexagonal lattice of the figure.
Casimir operators
The Casimir operator is an operator that commutes with all the generators of the Lie group. In the case of , the quadratic operator is the only independent such operator. In the case of group, by contrast, two independent Casimir operators can be constructed, a quadratic and a cubic: they are, : : These Casimir operators serve to label the irreducible representations of the Lie group algebra , because all states in a given representation assume the same value for each Casimir operator, which serves as the identity in a space with the dimension of that representation. This is because states in a given representation are connected by the action of the generators of the Lie algebra, and all generators commute with the Casimir operators. For example, for the triplet representation, , the eigenvalue of is 4/3, and of , 10/9. More generally, fromFreudenthal's formula
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by . There is a closely related formula for the ch ...
, for generic , the eigenvalue of is .
The eigenvalue ("anomaly coefficient") of is
It is an ''odd function'' under the interchange . Consequently, it vanishes for real representations , such as the adjoint, , i.e. both and anomalies vanish for it.
Representations of the SU(3) group
The irreducible representations of SU(3) are analyzed in various places, including Hall's book. Since the SU(3) group is simply connected, the representations are in one-to-one correspondence with the representations of its Lie algebra su(3), or the complexification of its Lie algebra, sl(3,C). We label the representations as ''D''(p,q), with ''p'' and ''q'' being non-negative integers, where in physical terms, ''p'' is the number of quarks and ''q'' is the number of antiquarks. Mathematically, the representation ''D''(p,q) may be constructed by tensoring together ''p'' copies of the standard 3-dimensional representation and ''q'' copies of the dual of the standard representation, and then extracting an irreducible invariant subspace. (See also the section of Young tableaux below: is the number of single-box columns, "quarks", and the number of double-box columns, "antiquarks"). Still another way to think about the parameters ''p'' and ''q'' is as the maximum eigenvalues of the diagonal matrices :. (The elements and are linear combinations of the elements and , but normalized so that the eigenvalues of and are integers.) This is to be compared to the representation theory of SU(2), where the irreducible representations are labeled by the maximum eigenvalue of a single element, ''h''. The representations have dimension/ref> :
 :
:
:
:
:
:
Here,
:
and
:
All the other states of the representation can be constructed by the successive application of the
:
:
:
:
:
:
Here,
:
and
:
All the other states of the representation can be constructed by the successive application of the ladder operator
In linear algebra (and its application to quantum mechanics), a raising or lowering operator (collectively known as ladder operators) is an operator that increases or decreases the eigenvalue of another operator. In quantum mechanics, the raisin ...
s and and by identifying the base states which are annihilated by the action of the lowering operators. These operators lie on the vertices and the center of a hexagon.
Clebsch–Gordan coefficient for SU(3)
The product representation of two irreducible representations and is generally reducible. Symbolically, : where is an integer. For example, two octets (adjoints) compose to : that is, their product reduces to an icosaseptet (27), decuplet, two octets, an antidecuplet, and a singlet, 64 states in all. The right-hand series is called the Clebsch–Gordan series. It implies that the representation appears times in the reduction of this direct product of with . Now a complete set of operators is needed to specify uniquely the states of each irreducible representation inside the one just reduced. Thecomplete set of commuting operators In quantum mechanics, a complete set of commuting observables (CSCO) is a set of commuting operators whose common eigenvectors can be used as a basis to express any quantum state. In the case of operators with discrete spectra, a CSCO is a set of c ...
in the case of the irreducible representation is
:
where
: .
The states of the above direct product representation are thus completely represented by the set of operators
:
where the number in the parentheses designates the representation on which the operator acts.
An alternate set of commuting operators can be found for the direct product representation, if one considers the following set of operators,
:
Thus, the set of commuting operators includes
:
This is a set of nine operators only. But the set must contain ten operators to define all the states of the direct product representation uniquely. To find the last operator , one must look outside the group. It is necessary to distinguish different for similar values of and .
:
Thus, any state in the direct product representation can be represented by the ket,
:
also using the second complete set of commuting operator, we can define the states in the direct product representation as
:
We can drop the from the state and label the states as
:
using the operators from the first set, and,
:
using the operators from the second set.
Both these states span the direct product representation and any states in the representation can be labeled by suitable choice of the eigenvalues.
Using the completeness relation,
Here, the coefficients
are the Clebsch–Gordan coefficients.
A different notation
To avoid confusion, the eigenvalues can be simultaneously denoted by and the eigenvalues are simultaneously denoted by . Then the eigenstate of the direct product representation can be denoted by : where is the eigenvalues of and is the eigenvalues of denoted simultaneously. Here, the quantity expressed by the parenthesis is the Wigner 3-j symbol. Furthermore, are considered to be the basis states of and are the basis states of . Also are the basis states of the product representation. Here represents the combined eigenvalues and respectively. Thus the unitary transformations that connects the two bases are : This is a comparatively compact notation. Here, : are the Clebsch–Gordan coefficients.Orthogonality relations
The Clebsch–Gordan coefficients form a real orthogonal matrix. Therefore, : Also, they follow the following orthogonality relations, : :Symmetry properties
If an irreducible representation appears in the Clebsch–Gordan series of , then it must appear in the Clebsch–Gordan series of . Which implies, : WhereSince the Clebsch–Gordan coefficients are all real, the following symmetry property can be deduced, : Where .
Symmetry group of the 3D oscillator Hamiltonian operator
A three-dimensional harmonic oscillator is described by the Hamiltonian : where the spring constant, the mass and Planck's constant have been absorbed into the definition of the variables, . It is seen that this Hamiltonian is symmetric under coordinate transformations that preserve the value of . Thus, any operators in the group keep this Hamiltonian invariant. More significantly, since the Hamiltonian is Hermitian, it further remains invariant under operation by elements of the much larger group. More systematically, operators such as theLadder operator
In linear algebra (and its application to quantum mechanics), a raising or lowering operator (collectively known as ladder operators) is an operator that increases or decreases the eigenvalue of another operator. In quantum mechanics, the raisin ...
s
: and
can be constructed which raise and lower the eigenvalue of the Hamiltonian operator by 1.
The operators and are not hermitian; but hermitian operators can be constructed from different combinations of them,
:namely, .
There are ''nine such operators'' for ''i,j''=1,2,3.
The nine hermitian operators formed by the bilinear forms are controlled by the fundamental commutators
:
:
and seen to ''not'' commute among themselves. As a result, this complete set of operators don't share their eigenvectors in common, and they cannot be diagonalized simultaneously. The group is thus non-Abelian and degeneracies may be present in the Hamiltonian, as indicated.
The Hamiltonian of the 3D isotropic harmonic oscillator, when written in terms of the operator amounts to
: