Chaos Theory

Chaos theory is an interdisciplinary area of scientific study and branch of mathematics focused on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions, and were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals, and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning that there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause a tornado in Texas.

Small differences in initial conditions, such as those due to errors in measurements or due to rounding errors in numerical computation, can yield widely diverging outcomes for such dynamical systems, rendering long-term prediction of their behavior impossible in general. This can happen even though these systems are deterministic, meaning that their future behavior follows a unique evolution and is fully determined by their initial conditions, with no random elements involved. In other words, the deterministic nature of these systems does not make them predictable. This behavior is known as deterministic chaos, or simply chaos. The theory was summarized by Edward Lorenz as:

Chaotic behavior exists in many natural systems, including fluid flow, heartbeat irregularities, weather, and climate. It also occurs spontaneously in some systems with artificial components, such as the road traffic. This behavior can be studied through the analysis of a chaotic mathematical model, or through analytical techniques such as recurrence plots and Poincaré maps. Chaos theory has applications in a variety of disciplines, including meteorology, anthropology, sociology, environmental science, computer science, engineering, economics, ecology, and pandemic crisis management. The theory formed the basis for such fields of study as complex dynamical systems, edge of chaos theory, and self-assembly processes.

Introduction

Chaos theory concerns deterministic systems whose behavior can, in principle, be predicted. Chaotic systems are predictable for a while and then 'appear' to become random. The amount of time for which the behavior of a chaotic system can be effectively predicted depends on three things: how much uncertainty can be tolerated in the forecast, how accurately its current state can be measured, and a time scale depending on the dynamics of the system, called the Lyapunov time. Some examples of Lyapunov times are: chaotic electrical circuits, about 1 millisecond; weather systems, a few days (unproven); the inner solar system, 4 to 5 million years. In chaotic systems, the uncertainty in a forecast increases exponentially with elapsed time. Hence, mathematically, doubling the forecast time more than squares the proportional uncertainty in the forecast. This means, in practice, a meaningful prediction cannot be made over an interval of more than two or three times the Lyapunov time. When meaningful predictions cannot be made, the system appears random.

Chaos theory is a method of qualitative and quantitative analysis to investigate the behavior of dynamic systems that cannot be explained and predicted by single data relationships, but must be explained and predicted by whole, continuous data relationships.

Chaotic dynamics

In common usage, "chaos" means "a state of disorder". However, in chaos theory, the term is defined more precisely. Although no universally accepted mathematical definition of chaos exists, a commonly used definition, originally formulated by Robert L. Devaney, says that to classify a dynamical system as chaotic, it must have these properties:

# it must be sensitive to initial conditions,
# it must be topologically transitive,
# it must have dense periodic orbits.

In some cases, the last two properties above have been shown to actually imply sensitivity to initial conditions. In the discrete-time case, this is true for all continuous maps on metric spaces. In these cases, while it is often the most practically significant property, "sensitivity to initial conditions" need not be stated in the definition.

If attention is restricted to intervals, the second property implies the other two. An alternative and a generally weaker definition of chaos uses only the first two properties in the above list.

Sensitivity to initial conditions

Sensitivity to initial conditions means that each point in a chaotic system is arbitrarily closely approximated by other points that have significantly different future paths or trajectories. Thus, an arbitrarily small change or perturbation of the current trajectory may lead to significantly different future behavior.

Sensitivity to initial conditions is popularly known as the " butterfly effect", so-called because of the title of a paper given by Edward Lorenz in 1972 to the American Association for the Advancement of Science in Washington, D.C., entitled ''Predictability: Does the Flap of a Butterfly's Wings in Brazil set off a Tornado in Texas?''. The flapping wing represents a small change in the initial condition of the system, which causes a chain of events that prevents the predictability of large-scale phenomena. Had the butterfly not flapped its wings, the trajectory of the overall system could have been vastly different.

As suggested in Lorenz's book entitled ''"The Essence of Chaos"'', published in 1993, ''"sensitive dependence can serve as an acceptable definition of chaos"''. In the same book, Lorenz defined the butterfly effect as: ''"The phenomenon that a small alteration in the state of a dynamical system will cause subsequent states to differ greatly from the states that would have followed without the alteration."'' The above definition is consistent with the sensitive dependence of solutions on initial conditions (SDIC). An idealized skiing model was developed to illustrate the sensitivity of time-varying paths to initial positions. A predictability horizon can be determined before the onset of SDIC (i.e., prior to significant separations of initial nearby trajectories).

A consequence of sensitivity to initial conditions is that if we start with a limited amount of information about the system (as is usually the case in practice), then beyond a certain time, the system would no longer be predictable. This is most prevalent in the case of weather, which is generally predictable only about a week ahead. This does not mean that one cannot assert anything about events far in the future—only that some restrictions on the system are present. For example, we know that the temperature of the surface of the earth will not naturally reach or fall below on earth (during the current geologic era), but we cannot predict exactly which day will have the hottest temperature of the year.

In more mathematical terms, the Lyapunov exponent measures the sensitivity to initial conditions, in the form of rate of exponential divergence from the perturbed initial conditions. More specifically, given two starting trajectories in the phase space that are infinitesimally close, with initial separation $\delta \mathbf_0$, the two trajectories end up diverging at a rate given by

:$, \delta\mathbf(t) , \approx e^ , \delta \mathbf_0 , ,$

where $t$ is the time and $\lambda$ is the Lyapunov exponent. The rate of separation depends on the orientation of the initial separation vector, so a whole spectrum of Lyapunov exponents can exist. The number of Lyapunov exponents is equal to the number of dimensions of the phase space, though it is common to just refer to the largest one. For example, the maximal Lyapunov exponent (MLE) is most often used, because it determines the overall predictability of the system. A positive MLE is usually taken as an indication that the system is chaotic.

In addition to the above property, other properties related to sensitivity of initial conditions also exist. These include, for example, measure-theoretical mixing (as discussed in ergodic theory) and properties of a K-system.

Non-periodicity

A chaotic system may have sequences of values for the evolving variable that exactly repeat themselves, giving periodic behavior starting from any point in that sequence. However, such periodic sequences are repelling rather than attracting, meaning that if the evolving variable is outside the sequence, however close, it will not enter the sequence and in fact, will diverge from it. Thus for almost all initial conditions, the variable evolves chaotically with non-periodic behavior.

Topological mixing

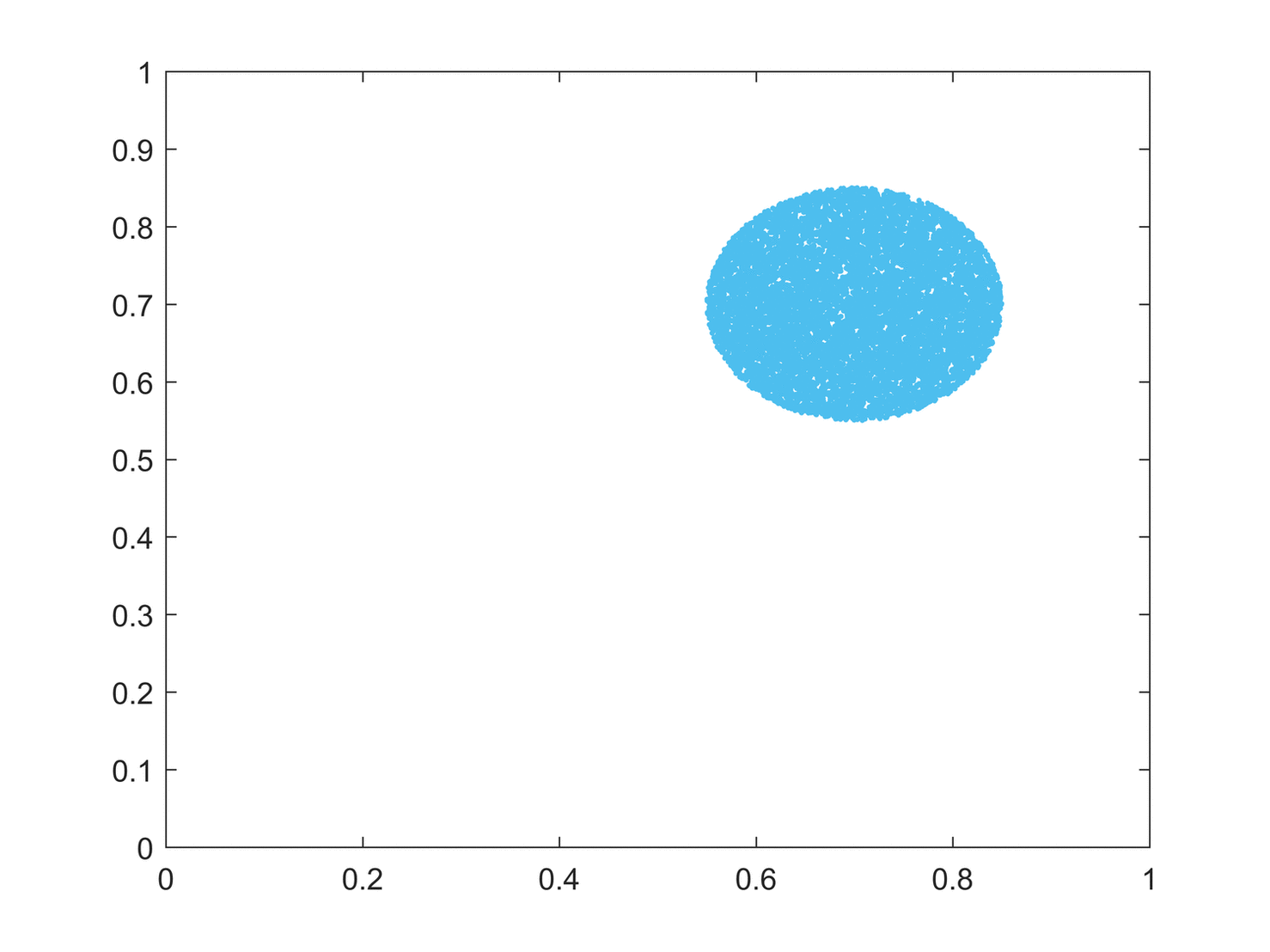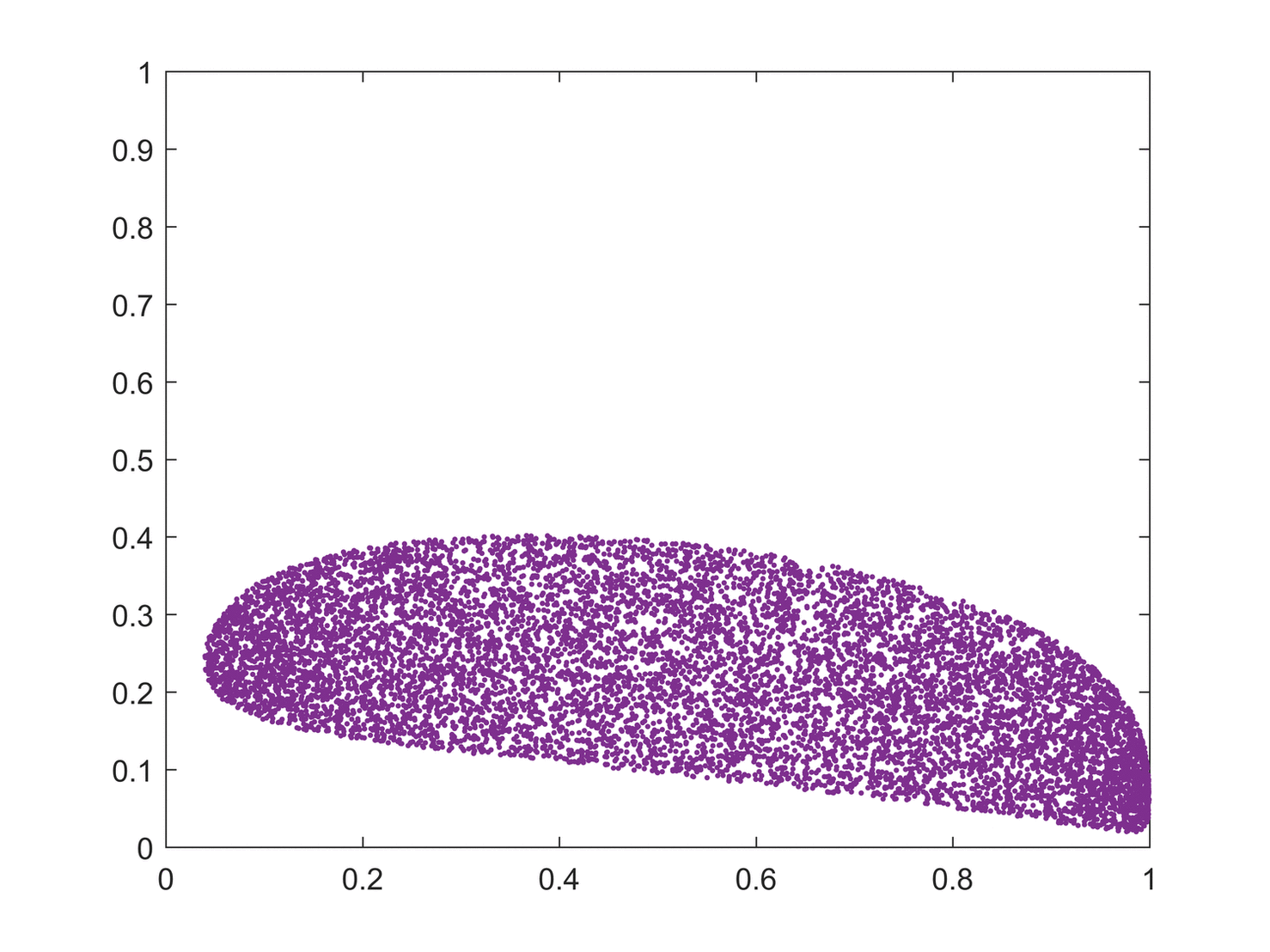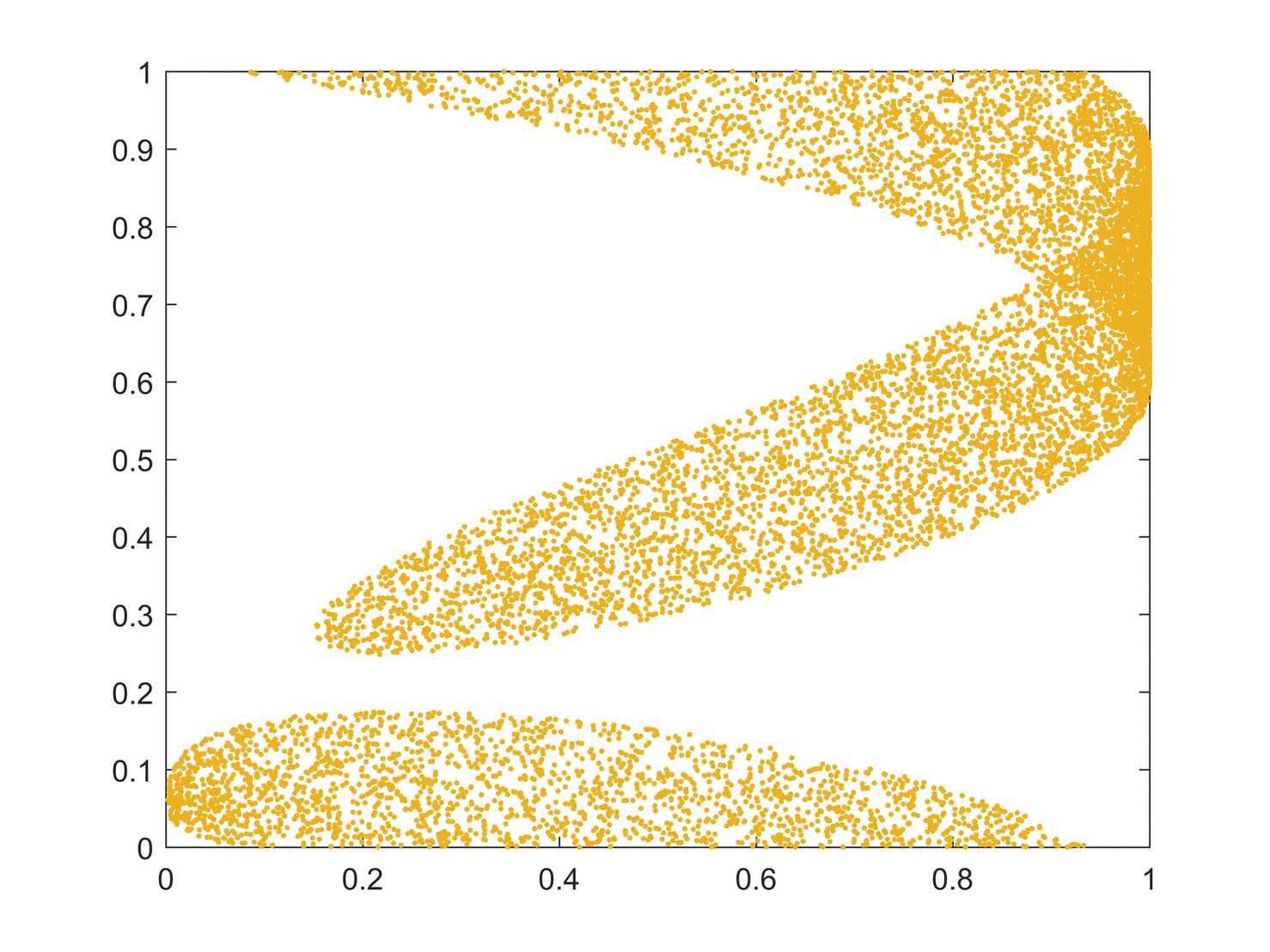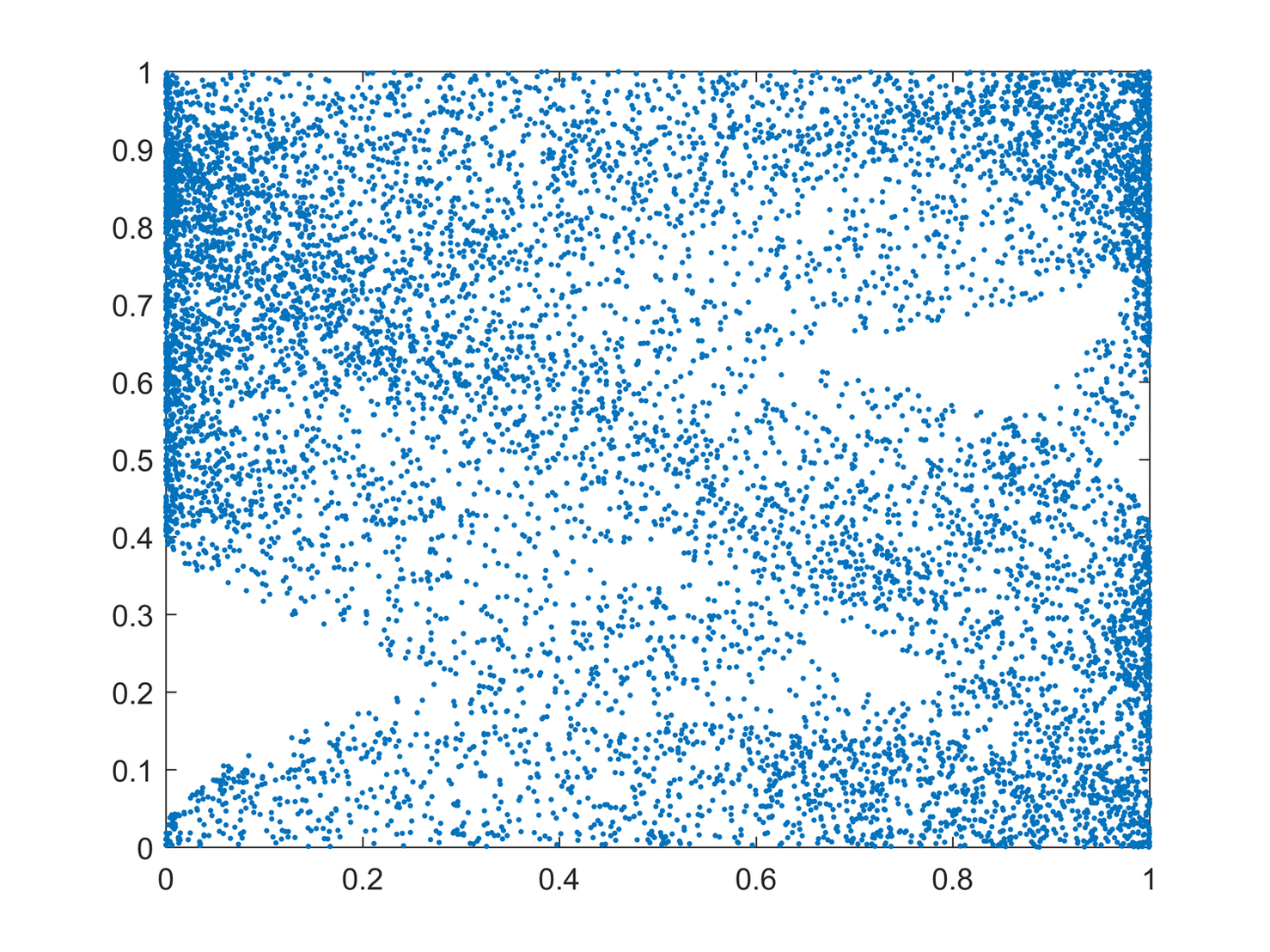Topological mixing (or the weaker condition of topological transitivity) means that the system evolves over time so that any given region or open set of its phase space eventually overlaps with any other given region. This mathematical concept of "mixing" corresponds to the standard intuition, and the mixing of colored dyes or fluids is an example of a chaotic system.

Topological mixing is often omitted from popular accounts of chaos, which equate chaos with only sensitivity to initial conditions. However, sensitive dependence on initial conditions alone does not give chaos. For example, consider the simple dynamical system produced by repeatedly doubling an initial value. This system has sensitive dependence on initial conditions everywhere, since any pair of nearby points eventually becomes widely separated. However, this example has no topological mixing, and therefore has no chaos. Indeed, it has extremely simple behavior: all points except 0 tend to positive or negative infinity.

Topological transitivity

A map $f:X \to X$ is said to be topologically transitive if for any pair of non-empty open sets $U, V \subset X$, there exists $k > 0$ such that $f^(U) \cap V \neq \emptyset$. Topological transitivity is a weaker version of topological mixing. Intuitively, if a map is topologically transitive then given a point ''x'' and a region ''V'', there exists a point ''y'' near ''x'' whose orbit passes through ''V''. This implies that it is impossible to decompose the system into two open sets.

An important related theorem is the Birkhoff Transitivity Theorem. It is easy to see that the existence of a dense orbit implies topological transitivity. The Birkhoff Transitivity Theorem states that if ''X'' is a second countable, complete metric space, then topological transitivity implies the existence of a dense set of points in ''X'' that have dense orbits.

Density of periodic orbits

For a chaotic system to have dense periodic orbits means that every point in the space is approached arbitrarily closely by periodic orbits. The one-dimensional logistic map defined by ''x'' → 4 ''x'' (1 – ''x'') is one of the simplest systems with density of periodic orbits. For example, $\tfrac$ → $\tfrac$ → $\tfrac$ (or approximately 0.3454915 → 0.9045085 → 0.3454915) is an (unstable) orbit of period 2, and similar orbits exist for periods 4, 8, 16, etc. (indeed, for all the periods specified by Sharkovskii's theorem).

Sharkovskii's theorem is the basis of the Li and Yorke (1975) proof that any continuous one-dimensional system that exhibits a regular cycle of period three will also display regular cycles of every other length, as well as completely chaotic orbits.

Strange attractors

Some dynamical systems, like the one-dimensional logistic map defined by ''x'' → 4 ''x'' (1 – ''x''), are chaotic everywhere, but in many cases chaotic behavior is found only in a subset of phase space. The cases of most interest arise when the chaotic behavior takes place on an attractor, since then a large set of initial conditions leads to orbits that converge to this chaotic region.

An easy way to visualize a chaotic attractor is to start with a point in the basin of attraction of the attractor, and then simply plot its subsequent orbit. Because of the topological transitivity condition, this is likely to produce a picture of the entire final attractor, and indeed both orbits shown in the figure on the right give a picture of the general shape of the Lorenz attractor. This attractor results from a simple three-dimensional model of the Lorenz weather system. The Lorenz attractor is perhaps one of the best-known chaotic system diagrams, probably because it is not only one of the first, but it is also one of the most complex, and as such gives rise to a very interesting pattern that, with a little imagination, looks like the wings of a butterfly.

Unlike fixed-point attractors and limit cycles, the attractors that arise from chaotic systems, known as strange attractors, have great detail and complexity. Strange attractors occur in both continuous dynamical systems (such as the Lorenz system) and in some discrete systems (such as the Hénon map). Other discrete dynamical systems have a repelling structure called a Julia set, which forms at the boundary between basins of attraction of fixed points. Julia sets can be thought of as strange repellers. Both strange attractors and Julia sets typically have a fractal structure, and the fractal dimension can be calculated for them.

Coexisting attractors

In contrast to single type chaotic solutions, recent studies using Lorenz models have emphasized the importance of considering various types of solutions. For example, coexisting chaotic and non-chaotic may appear within the same model (e.g., the double pendulum system) using the same modeling configurations but different initial conditions. The findings of attractor coexistence, obtained from classical and generalized Lorenz models, suggested a revised view that “the entirety of weather possesses a dual nature of chaos and order with distinct predictability”, in contrast to the conventional view of “weather is chaotic”.

Minimum complexity of a chaotic system

Discrete chaotic systems, such as the logistic map, can exhibit strange attractors whatever their dimensionality. Universality of one-dimensional maps with parabolic maxima and Feigenbaum constants $\delta=4.669201...$,$\alpha=2.502907...$ is well visible with map proposed as a toy
model for discrete laser dynamics:
$x \rightarrow G x (1 - \mathrm (x))$,
where $x$ stands for electric field amplitude, $G$ is laser gain as bifurcation parameter. The gradual increase of $G$ at interval _with_qualitatively_the_same_ _with_qualitatively_the_same_bifurcation_diagram">,_\infty)_changes_dynamics_from_regular_to_chaotic_one_with_qualitatively_the_same_bifurcation_diagram_as_those_for__logistic_map.

In_contrast,_for_continuous_function_(topology).html" ;"title="bifurcation_diagram.html" ;"title=", \infty) changes dynamics from regular to chaotic one with qualitatively the same bifurcation diagram">, \infty) changes dynamics from regular to chaotic one with qualitatively the same bifurcation diagram as those for logistic map.

In contrast, for continuous function (topology)">continuous dynamical systems, the Poincaré–Bendixson theorem shows that a strange attractor can only arise in three or more dimensions. Dimension (vector space), Finite-dimensional linear systems are never chaotic; for a dynamical system to display chaotic behavior, it must be either nonlinear or infinite-dimensional.

The Poincaré–Bendixson theorem states that a two-dimensional differential equation has very regular behavior. The Lorenz attractor discussed below is generated by a system of three differential equations such as:
: $\begin \frac &= \sigma y - \sigma x, \\ \frac &= \rho x - x z - y, \\ \frac &= x y - \beta z. \end$
where $x$, $y$, and $z$ make up the system state, $t$ is time, and $\sigma$, $\rho$, $\beta$ are the system parameters. Five of the terms on the right hand side are linear, while two are quadratic; a total of seven terms. Another well-known chaotic attractor is generated by the Rössler equations, which have only one nonlinear term out of seven. Sprott found a three-dimensional system with just five terms, that had only one nonlinear term, which exhibits chaos for certain parameter values. Zhang and Heidel showed that, at least for dissipative and conservative quadratic systems, three-dimensional quadratic systems with only three or four terms on the right-hand side cannot exhibit chaotic behavior. The reason is, simply put, that solutions to such systems are asymptotic to a two-dimensional surface and therefore solutions are well behaved.

While the Poincaré–Bendixson theorem shows that a continuous dynamical system on the Euclidean plane cannot be chaotic, two-dimensional continuous systems with non-Euclidean geometry can exhibit chaotic behavior. Perhaps surprisingly, chaos may occur also in linear systems, provided they are infinite dimensional. A theory of linear chaos is being developed in a branch of mathematical analysis known as functional analysis.

The above elegant set of three ordinary differential equations has been referred to as the three-dimensional Lorenz model. Since 1963, higher-dimensional Lorenz models have been developed in numerous studies for examining the impact of an increased degree of nonlinearity, as well as its collective effect with heating and dissipations, on solution stability.

Infinite dimensional maps

The straightforward generalization of coupled discrete maps is based upon convolution integral which mediates interaction between spatially distributed maps:
\psi_(\vec r,t) = \int K(\vec r - \vec r^,t) f psi_(\vec r^,t) ^,

where kernel $K(\vec r - \vec r^,t)$ is propagator derived as Green function of a relevant physical system,
f psi_(\vec r,t) might be logistic map alike \psi \rightarrow G \psi - \tanh (\psi)/math> or complex map. For examples of complex maps the Julia set f psi= \psi^2 or Ikeda map
$\psi_ = A + B \psi_n e^$ may serve. When wave propagation problems at distance $L=ct$ with wavelength $\lambda=2\pi/k$ are considered the kernel $K$ may have a form of Green function for Schrödinger equation:.

K(\vec r - \vec r^,L) = \frac \exp frac /math>.

Jerk systems

In physics, jerk is the third derivative of position, with respect to time. As such, differential equations of the form
:: $J\left(\overset,\ddot,\dot ,x\right)=0$
are sometimes called ''jerk equations''. It has been shown that a jerk equation, which is equivalent to a system of three first order, ordinary, non-linear differential equations, is in a certain sense the minimal setting for solutions showing chaotic behavior. This motivates mathematical interest in jerk systems. Systems involving a fourth or higher derivative are called accordingly hyperjerk systems.

A jerk system's behavior is described by a jerk equation, and for certain jerk equations, simple electronic circuits can model solutions. These circuits are known as jerk circuits.

One of the most interesting properties of jerk circuits is the possibility of chaotic behavior. In fact, certain well-known chaotic systems, such as the Lorenz attractor and the Rössler map, are conventionally described as a system of three first-order differential equations that can combine into a single (although rather complicated) jerk equation. Another example of a jerk equation with nonlinearity in the magnitude of $x$ is:
:$\frac+A\frac+\frac-, x, +1=0.$

Here, ''A'' is an adjustable parameter. This equation has a chaotic solution for ''A''=3/5 and can be implemented with the following jerk circuit; the required nonlinearity is brought about by the two diodes:

In the above circuit, all resistors are of equal value, except $R_A=R/A=5R/3$, and all capacitors are of equal size. The dominant frequency is $1/2\pi R C$. The output of op amp 0 will correspond to the x variable, the output of 1 corresponds to the first derivative of x and the output of 2 corresponds to the second derivative.

Similar circuits only require one diode or no diodes at all.

See also the well-known Chua's circuit, one basis for chaotic true random number generators. The ease of construction of the circuit has made it a ubiquitous real-world example of a chaotic system.

Spontaneous order

Under the right conditions, chaos spontaneously evolves into a lockstep pattern. In the Kuramoto model, four conditions suffice to produce synchronization in a chaotic system.
Examples include the coupled oscillation of Christiaan Huygens' pendulums, fireflies, neurons, the London Millennium Bridge resonance, and large arrays of Josephson junctions.

History

An early proponent of chaos theory was Henri Poincaré. In the 1880s, while studying the three-body problem, he found that there can be orbits that are nonperiodic, and yet not forever increasing nor approaching a fixed point. In 1898, Jacques Hadamard published an influential study of the chaotic motion of a free particle gliding frictionlessly on a surface of constant negative curvature, called " Hadamard's billiards". Hadamard was able to show that all trajectories are unstable, in that all particle trajectories diverge exponentially from one another, with a positive Lyapunov exponent.

Chaos theory began in the field of ergodic theory. Later studies, also on the topic of nonlinear differential equations, were carried out by George David Birkhoff, Andrey Nikolaevich Kolmogorov, Mary Lucy Cartwright and John Edensor Littlewood, and Stephen Smale. Except for Smale, these studies were all directly inspired by physics: the three-body problem in the case of Birkhoff, turbulence and astronomical problems in the case of Kolmogorov, and radio engineering in the case of Cartwright and Littlewood. Although chaotic planetary motion had not been observed, experimentalists had encountered turbulence in fluid motion and nonperiodic oscillation in radio circuits without the benefit of a theory to explain what they were seeing.

Despite initial insights in the first half of the twentieth century, chaos theory became formalized as such only after mid-century, when it first became evident to some scientists that linear theory, the prevailing system theory at that time, simply could not explain the observed behavior of certain experiments like that of the logistic map. What had been attributed to measure imprecision and simple "noise" was considered by chaos theorists as a full component of the studied systems.

The main catalyst for the development of chaos theory was the electronic computer. Much of the mathematics of chaos theory involves the repeated iteration of simple mathematical formulas, which would be impractical to do by hand. Electronic computers made these repeated calculations practical, while figures and images made it possible to visualize these systems. As a graduate student in Chihiro Hayashi's laboratory at Kyoto University, Yoshisuke Ueda was experimenting with analog computers and noticed, on November 27, 1961, what he called "randomly transitional phenomena". Yet his advisor did not agree with his conclusions at the time, and did not allow him to report his findings until 1970.

Edward Lorenz was an early pioneer of the theory. His interest in chaos came about accidentally through his work on weather prediction in 1961. Lorenz and his collaborator Ellen Fetter were using a simple digital computer, a Royal McBee LGP-30, to run weather simulations. They wanted to see a sequence of data again, and to save time they started the simulation in the middle of its course. They did this by entering a printout of the data that corresponded to conditions in the middle of the original simulation. To their surprise, the weather the machine began to predict was completely different from the previous calculation. They tracked this down to the computer printout. The computer worked with 6-digit precision, but the printout rounded variables off to a 3-digit number, so a value like 0.506127 printed as 0.506. This difference is tiny, and the consensus at the time would have been that it should have no practical effect. However, Lorenz discovered that small changes in initial conditions produced large changes in long-term outcome. Lorenz's discovery, which gave its name to Lorenz attractors, showed that even detailed atmospheric modeling cannot, in general, make precise long-term weather predictions.

In 1963, Benoit Mandelbrot found recurring patterns at every scale in data on cotton prices. Beforehand he had studied information theory and concluded noise was patterned like a Cantor set: on any scale the proportion of noise-containing periods to error-free periods was a constant – thus errors were inevitable and must be planned for by incorporating redundancy. Mandelbrot described both the "Noah effect" (in which sudden discontinuous changes can occur) and the "Joseph effect" (in which persistence of a value can occur for a while, yet suddenly change afterwards). This challenged the idea that changes in price were normally distributed. In 1967, he published "How long is the coast of Britain? Statistical self-similarity and fractional dimension", showing that a coastline's length varies with the scale of the measuring instrument, resembles itself at all scales, and is infinite in length for an infinitesimally small measuring device. Arguing that a ball of twine appears as a point when viewed from far away (0-dimensional), a ball when viewed from fairly near (3-dimensional), or a curved strand (1-dimensional), he argued that the dimensions of an object are relative to the observer and may be fractional. An object whose irregularity is constant over different scales ("self-similarity") is a fractal (examples include the Menger sponge, the Sierpiński gasket, and the Koch curve or ''snowflake'', which is infinitely long yet encloses a finite space and has a fractal dimension of circa 1.2619). In 1982, Mandelbrot published '' The Fractal Geometry of Nature'', which became a classic of chaos theory.

In December 1977, the New York Academy of Sciences organized the first symposium on chaos, attended by David Ruelle, Robert May, James A. Yorke (coiner of the term "chaos" as used in mathematics), Robert Shaw, and the meteorologist Edward Lorenz. The following year Pierre Coullet and Charles Tresser published "Itérations d'endomorphismes et groupe de renormalisation", and Mitchell Feigenbaum's article "Quantitative Universality for a Class of Nonlinear Transformations" finally appeared in a journal, after 3 years of referee rejections. Thus Feigenbaum (1975) and Coullet & Tresser (1978) discovered the universality in chaos, permitting the application of chaos theory to many different phenomena.

In 1979, Albert J. Libchaber, during a symposium organized in Aspen by Pierre Hohenberg, presented his experimental observation of the bifurcation cascade that leads to chaos and turbulence in Rayleigh–Bénard convection systems. He was awarded the Wolf Prize in Physics in 1986 along with Mitchell J. Feigenbaum for their inspiring achievements.

In 1986, the New York Academy of Sciences co-organized with the National Institute of Mental Health and the Office of Naval Research the first important conference on chaos in biology and medicine. There, Bernardo Huberman presented a mathematical model of the eye tracking dysfunction among people with schizophrenia. This led to a renewal of physiology in the 1980s through the application of chaos theory, for example, in the study of pathological cardiac cycles.

In 1987, Per Bak, Chao Tang and Kurt Wiesenfeld published a paper in ''Physical Review Letters'' describing for the first time self-organized criticality (SOC), considered one of the mechanisms by which complexity arises in nature.

Alongside largely lab-based approaches such as the Bak–Tang–Wiesenfeld sandpile, many other investigations have focused on large-scale natural or social systems that are known (or suspected) to display scale-invariant behavior. Although these approaches were not always welcomed (at least initially) by specialists in the subjects examined, SOC has nevertheless become established as a strong candidate for explaining a number of natural phenomena, including earthquakes, (which, long before SOC was discovered, were known as a source of scale-invariant behavior such as the Gutenberg–Richter law describing the statistical distribution of earthquake sizes, and the Omori law describing the frequency of aftershocks), solar flares, fluctuations in economic systems such as financial markets (references to SOC are common in econophysics), landscape formation, forest fires, landslides, epidemics, and biological evolution (where SOC has been invoked, for example, as the dynamical mechanism behind the theory of " punctuated equilibria" put forward by Niles Eldredge and Stephen Jay Gould). Given the implications of a scale-free distribution of event sizes, some researchers have suggested that another phenomenon that should be considered an example of SOC is the occurrence of wars. These investigations of SOC have included both attempts at modelling (either developing new models or adapting existing ones to the specifics of a given natural system), and extensive data analysis to determine the existence and/or characteristics of natural scaling laws.

In the same year, James Gleick published '' Chaos: Making a New Science'', which became a best-seller and introduced the general principles of chaos theory as well as its history to the broad public. Initially the domain of a few, isolated individuals, chaos theory progressively emerged as a transdisciplinary and institutional discipline, mainly under the name of nonlinear systems analysis. Alluding to Thomas Kuhn's concept of a paradigm shift exposed in ''The Structure of Scientific Revolutions'' (1962), many "chaologists" (as some described themselves) claimed that this new theory was an example of such a shift, a thesis upheld by Gleick.

The availability of cheaper, more powerful computers broadens the applicability of chaos theory. Currently, chaos theory remains an active area of research, involving many different disciplines such as mathematics, topology, physics, social systems, population modeling, biology, meteorology, astrophysics, information theory, computational neuroscience, pandemic crisis management, etc.

Applications

Although chaos theory was born from observing weather patterns, it has become applicable to a variety of other situations. Some areas benefiting from chaos theory today are geology, mathematics, biology, computer science, economics, engineering, finance, meteorology, philosophy, anthropology, physics, politics, population dynamics, and robotics. A few categories are listed below with examples, but this is by no means a comprehensive list as new applications are appearing.

Cryptography

Chaos theory has been used for many years in cryptography. In the past few decades, chaos and nonlinear dynamics have been used in the design of hundreds of cryptographic primitives. These algorithms include image encryption algorithms, hash functions, secure pseudo-random number generators, stream ciphers, watermarking, and steganography. The majority of these algorithms are based on uni-modal chaotic maps and a big portion of these algorithms use the control parameters and the initial condition of the chaotic maps as their keys. From a wider perspective, without loss of generality, the similarities between the chaotic maps and the cryptographic systems is the main motivation for the design of chaos based cryptographic algorithms. One type of encryption, secret key or symmetric key, relies on diffusion and confusion, which is modeled well by chaos theory. Another type of computing, DNA computing, when paired with chaos theory, offers a way to encrypt images and other information. Many of the DNA-Chaos cryptographic algorithms are proven to be either not secure, or the technique applied is suggested to be not efficient.

Robotics

Robotics is another area that has recently benefited from chaos theory. Instead of robots acting in a trial-and-error type of refinement to interact with their environment, chaos theory has been used to build a predictive model.
Chaotic dynamics have been exhibited by passive walking biped robots.

Biology

For over a hundred years, biologists have been keeping track of populations of different species with population models. Most models are continuous, but recently scientists have been able to implement chaotic models in certain populations. For example, a study on models of Canadian lynx showed there was chaotic behavior in the population growth. Chaos can also be found in ecological systems, such as hydrology. While a chaotic model for hydrology has its shortcomings, there is still much to learn from looking at the data through the lens of chaos theory. Another biological application is found in cardiotocography. Fetal surveillance is a delicate balance of obtaining accurate information while being as noninvasive as possible. Better models of warning signs of fetal hypoxia can be obtained through chaotic modeling.

Economics

It is possible that economic models can also be improved through an application of chaos theory, but predicting the health of an economic system and what factors influence it most is an extremely complex task. Economic and financial systems are fundamentally different from those in the classical natural sciences since the former are inherently stochastic in nature, as they result from the interactions of people, and thus pure deterministic models are unlikely to provide accurate representations of the data. The empirical literature that tests for chaos in economics and finance presents very mixed results, in part due to confusion between specific tests for chaos and more general tests for non-linear relationships.

Chaos could be found in economics by the means of recurrence quantification analysis. In fact, Orlando et al. by the means of the so-called recurrence quantification correlation index were able detect hidden changes in time series. Then, the same technique was employed to detect transitions from laminar (regular) to turbulent (chaotic) phases as well as differences between macroeconomic variables and highlight hidden features of economic dynamics. Finally, chaos could help in modeling how economy operate as well as in embedding shocks due to external events such as COVID-19.

Other areas

In chemistry, predicting gas solubility is essential to manufacturing polymers, but models using particle swarm optimization (PSO) tend to converge to the wrong points. An improved version of PSO has been created by introducing chaos, which keeps the simulations from getting stuck. In celestial mechanics, especially when observing asteroids, applying chaos theory leads to better predictions about when these objects will approach Earth and other planets. Four of the five moons of Pluto rotate chaotically. In quantum physics and electrical engineering, the study of large arrays of Josephson junctions benefitted greatly from chaos theory. Closer to home, coal mines have always been dangerous places where frequent natural gas leaks cause many deaths. Until recently, there was no reliable way to predict when they would occur. But these gas leaks have chaotic tendencies that, when properly modeled, can be predicted fairly accurately.

Chaos theory can be applied outside of the natural sciences, but historically nearly all such studies have suffered from lack of reproducibility; poor external validity; and/or inattention to cross-validation, resulting in poor predictive accuracy (if out-of-sample prediction has even been attempted). Glass and Mandell and Selz have found that no EEG study has as yet indicated the presence of strange attractors or other signs of chaotic behavior.

Researchers have continued to apply chaos theory to psychology. For example, in modeling group behavior in which heterogeneous members may behave as if sharing to different degrees what in Wilfred Bion's theory is a basic assumption, researchers have found that the group dynamic is the result of the individual dynamics of the members: each individual reproduces the group dynamics in a different scale, and the chaotic behavior of the group is reflected in each member.

Redington and Reidbord (1992) attempted to demonstrate that the human heart could display chaotic traits. They monitored the changes in between-heartbeat intervals for a single psychotherapy patient as she moved through periods of varying emotional intensity during a therapy session. Results were admittedly inconclusive. Not only were there ambiguities in the various plots the authors produced to purportedly show evidence of chaotic dynamics (spectral analysis, phase trajectory, and autocorrelation plots), but also when they attempted to compute a Lyapunov exponent as more definitive confirmation of chaotic behavior, the authors found they could not reliably do so.

In their 1995 paper, Metcalf and Allen maintained that they uncovered in animal behavior a pattern of period doubling leading to chaos. The authors examined a well-known response called schedule-induced polydipsia, by which an animal deprived of food for certain lengths of time will drink unusual amounts of water when the food is at last presented. The control parameter (r) operating here was the length of the interval between feedings, once resumed. The authors were careful to test a large number of animals and to include many replications, and they designed their experiment so as to rule out the likelihood that changes in response patterns were caused by different starting places for r.

Time series and first delay plots provide the best support for the claims made, showing a fairly clear march from periodicity to irregularity as the feeding times were increased. The various phase trajectory plots and spectral analyses, on the other hand, do not match up well enough with the other graphs or with the overall theory to lead inexorably to a chaotic diagnosis. For example, the phase trajectories do not show a definite progression towards greater and greater complexity (and away from periodicity); the process seems quite muddied. Also, where Metcalf and Allen saw periods of two and six in their spectral plots, there is room for alternative interpretations. All of this ambiguity necessitate some serpentine, post-hoc explanation to show that results fit a chaotic model.

By adapting a model of career counseling to include a chaotic interpretation of the relationship between employees and the job market, Amundson and Bright found that better suggestions can be made to people struggling with career decisions. Modern organizations are increasingly seen as open complex adaptive systems with fundamental natural nonlinear structures, subject to internal and external forces that may contribute chaos. For instance, team building and group development is increasingly being researched as an inherently unpredictable system, as the uncertainty of different individuals meeting for the first time makes the trajectory of the team unknowable.

Some say the chaos metaphor—used in verbal theories—grounded on mathematical models and psychological aspects of human behavior
provides helpful insights to describing the complexity of small work groups, that go beyond the metaphor itself.

Traffic forecasting may benefit from applications of chaos theory. Better predictions of when a congestion will occur would allow measures to be taken to disperse it before it would have occurred. Combining chaos theory principles with a few other methods has led to a more accurate short-term prediction model (see the plot of the BML traffic model at right).

Chaos theory has been applied to environmental water cycle data (also hydrological data), such as rainfall and streamflow. These studies have yielded controversial results, because the methods for detecting a chaotic signature are often relatively subjective. Early studies tended to "succeed" in finding chaos, whereas subsequent studies and meta-analyses called those studies into question and provided explanations for why these datasets are not likely to have low-dimension chaotic dynamics.

See also

Examples of chaotic systems

* Advected contours
* Arnold's cat map
* Bifurcation theory
* Bouncing ball dynamics
* Chua's circuit
* Cliodynamics
* Coupled map lattice
* Double pendulum
* Duffing equation
* Dynamical billiards
* Economic bubble
* Gaspard-Rice system
* Hénon map
* Horseshoe map
* List of chaotic maps
* Rössler attractor
* Standard map
* Swinging Atwood's machine
* Tilt A Whirl

Other related topics

* Amplitude death
* Anosov diffeomorphism
* Catastrophe theory
* Causality
* Chaos machine
* Chaotic mixing
* Chaotic scattering
* Control of chaos
* Determinism
* Edge of chaos
* Emergence
* Mandelbrot set
* Kolmogorov–Arnold–Moser theorem
* Ill-conditioning
* Ill-posedness
* Nonlinear system
* Patterns in nature
* Predictability
* Quantum chaos
* Santa Fe Institute
* Synchronization of chaos
* Unintended consequence
* Chaos as topological supersymmetry breaking

People

* Ralph Abraham
* Michael Berry
* Leon O. Chua
* Ivar Ekeland
* Doyne Farmer
* Martin Gutzwiller
* Brosl Hasslacher
* Michel Hénon
* Aleksandr Lyapunov
* Norman Packard
* Otto Rössler
* David Ruelle
* Oleksandr Mikolaiovich Sharkovsky
* Robert Shaw
* Floris Takens
* James A. Yorke
* George M. Zaslavsky

References

Further reading

Articles

*
*
*
*
Online version
(Note: the volume and page citation cited for the online text differ from that cited here. The citation here is from a photocopy, which is consistent with other citations found online that don't provide article views. The online content is identical to the hardcopy text. Citation variations are related to country of publication).
*
*
*
*
*

Textbooks

*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*

Semitechnical and popular works

* Christophe Letellier, ''Chaos in Nature'', World Scientific Publishing Company, 2012, .
*
*
*
* John Briggs and David Peat, ''Turbulent Mirror: : An Illustrated Guide to Chaos Theory and the Science of Wholeness'', Harper Perennial 1990, 224 pp.
* John Briggs and David Peat, ''Seven Life Lessons of Chaos: Spiritual Wisdom from the Science of Change'', Harper Perennial 2000, 224 pp.
*
* Predrag Cvitanović, ''Universality in Chaos'', Adam Hilger 1989, 648 pp.
* Leon Glass and Michael C. Mackey, ''From Clocks to Chaos: The Rhythms of Life,'' Princeton University Press 1988, 272 pp.
* James Gleick, '' Chaos: Making a New Science'', New York: Penguin, 1988. 368 pp.
*
* L Douglas Kiel, Euel W Elliott (ed.), ''Chaos Theory in the Social Sciences: Foundations and Applications'', University of Michigan Press, 1997, 360 pp.
* Arvind Kumar, ''Chaos, Fractals and Self-Organisation; New Perspectives on Complexity in Nature '', National Book Trust, 2003.
* Hans Lauwerier, ''Fractals'', Princeton University Press, 1991.
* Edward Lorenz, ''The Essence of Chaos'', University of Washington Press, 1996.
*
* David Peak and Michael Frame, ''Chaos Under Control: The Art and Science of Complexity'', Freeman, 1994.
* Heinz-Otto Peitgen and Dietmar Saupe (Eds.), ''The Science of Fractal Images'', Springer 1988, 312 pp.
* Nuria Perpinya, ''Caos, virus, calma. La Teoría del Caos aplicada al desórden artístico, social y político'', Páginas de Espuma, 2021.
* Clifford A. Pickover, ''Computers, Pattern, Chaos, and Beauty: Graphics from an Unseen World '', St Martins Pr 1991.
* Clifford A. Pickover, ''Chaos in Wonderland: Visual Adventures in a Fractal World'', St Martins Pr 1994.
* Ilya Prigogine and Isabelle Stengers, ''Order Out of Chaos'', Bantam 1984.
*
* David Ruelle, ''Chance and Chaos'', Princeton University Press 1993.
* Ivars Peterson, ''Newton's Clock: Chaos in the Solar System'', Freeman, 1993.
*
*
* Manfred Schroeder, ''Fractals, Chaos, and Power Laws'', Freeman, 1991.
*
* Ian Stewart, ''Does God Play Dice?: The Mathematics of Chaos '', Blackwell Publishers, 1990.
* Steven Strogatz, ''Sync: The emerging science of spontaneous order'', Hyperion, 2003.
* Yoshisuke Ueda, ''The Road To Chaos'', Aerial Pr, 1993.
* M. Mitchell Waldrop, ''Complexity : The Emerging Science at the Edge of Order and Chaos'', Simon & Schuster, 1992.
* Antonio Sawaya, ''Financial Time Series Analysis : Chaos and Neurodynamics Approach'', Lambert, 2012.

External links

*

Nonlinear Dynamics Research Group
with Animations in Flash

The Chaos group at the University of Maryland

The Chaos Hypertextbook
An introductory primer on chaos and fractals

ChaosBook.org
An advanced graduate textbook on chaos (no fractals)

Society for Chaos Theory in Psychology & Life Sciences


Florence Italy

Nonlinear dynamics: how science comprehends chaos
talk presented by Sunny Auyang, 1998.

Nonlinear Dynamics
Models of bifurcation and chaos by Elmer G. Wiens




Systems Analysis, Modelling and Prediction Group
at the University of Oxford

A page about the Mackey-Glass equation

High Anxieties — The Mathematics of Chaos
(2008) BBC documentary directed by David Malone

The chaos theory of evolution
– article published in Newscientist featuring similarities of evolution and non-linear systems including fractal nature of life and chaos.
* Jos Leys, Étienne Ghys et Aurélien Alvarez
''Chaos, A Mathematical Adventure''
Nine films about dynamical systems, the butterfly effect and chaos theory, intended for a wide audience.

"Chaos Theory"
BBC Radio 4 discussion with Susan Greenfield, David Papineau & Neil Johnson (''In Our Time'', May 16, 2002)

Chaos: The Science of the Butterfly Effect
(2019) an explanation presented by Derek Muller

{{DEFAULTSORT:Chaos Theory

Complex systems theory
Computational fields of study