Cauchy condensation test on:
[Wikipedia]
[Google]
[Amazon]
In
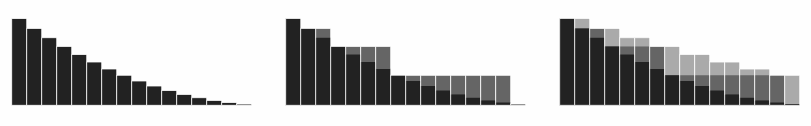
Extending tests for convergence of number series
page 7/28 via
Cauchy condensation test proof
{{Calculus topics Augustin-Louis Cauchy Convergence tests
mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, the Cauchy condensation test, named after Augustin-Louis Cauchy
Baron Augustin-Louis Cauchy (, ; ; 21 August 178923 May 1857) was a French mathematician, engineer, and physicist who made pioneering contributions to several branches of mathematics, including mathematical analysis and continuum mechanics. H ...
, is a standard convergence test for infinite series
In mathematics, a series is, roughly speaking, a description of the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, math ...
. For a non-increasing
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is called ...
sequence
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is called ...
of non-negative real number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every ...
s, the series converges if and only if the "condensed" series converges. Moreover, if they converge, the sum of the condensed series is no more than twice as large as the sum of the original.
Estimate
The Cauchy condensation test follows from the stronger estimate, which should be understood as aninequality
Inequality may refer to:
Economics
* Attention inequality, unequal distribution of attention across users, groups of people, issues in etc. in attention economy
* Economic inequality, difference in economic well-being between population groups
* ...
of extended real numbers
In mathematics, the affinely extended real number system is obtained from the real number system \R by adding two infinity elements: +\infty and -\infty, where the infinities are treated as actual numbers. It is useful in describing the algebra on ...
. The essential thrust of a proof
Proof most often refers to:
* Proof (truth), argument or sufficient evidence for the truth of a proposition
* Alcohol proof, a measure of an alcoholic drink's strength
Proof may also refer to:
Mathematics and formal logic
* Formal proof, a c ...
follows, patterned after Oresme's proof of the divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the quantity of the vector field's source at each point. More technically, the divergence represents the volume density of ...
of the harmonic series.
To see the first inequality, the terms of the original series are rebracketed into runs whose lengths are powers of two
A power of two is a number of the form where is an integer, that is, the result of exponentiation with number two as the base and integer as the exponent.
In a context where only integers are considered, is restricted to non-negati ...
, and then each run is bounded above by replacing each term by the largest term in that run. That term is always the first one, since by assumption the terms are non-increasing.
To see the second inequality, these two series are again rebracketed into runs of power of two length, but "offset" as shown below, so that the run of which ''begins'' with lines up with the end of the run of which ''ends'' with , so that the former stays always "ahead" of the latter.
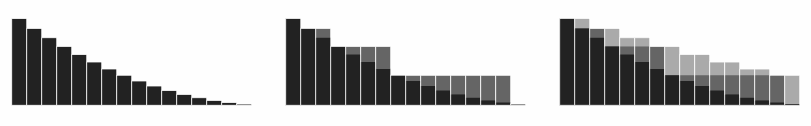
Integral comparison
The "condensation" transformation recalls theintegral
In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with ...
variable substitution yielding .
Pursuing this idea, the integral test for convergence gives us, in the case of monotone
Monotone refers to a sound, for example music or speech, that has a single unvaried tone. See: monophony.
Monotone or monotonicity may also refer to:
In economics
*Monotone preferences, a property of a consumer's preference ordering.
*Monotonic ...
, that converges if and only if converges. The substitution yields the integral . We then notice that , where the right hand side comes from applying the integral test to the condensed series . Therefore, converges if and only if converges.
Examples
The test can be useful for series where appears as in a denominator in . For the most basic example of this sort, the harmonic series is transformed into the series , which clearly diverges. As a more complex example, take Here the series definitely converges for , and diverges for . When , the condensation transformation gives the series Thelogarithm
In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a number to the base is the exponent to which must be raised, to produce . For example, since , the ''logarithm base'' 10 ...
s "shift to the left". So when , we have convergence for , divergence for . When the value of enters.
This result readily generalizes: the condensation test, applied repeatedly, can be used to show that for , the generalized Bertrand series converges for and diverges for . Here denotes the th iterate
Iteration is the repetition of a process in order to generate a (possibly unbounded) sequence of outcomes. Each repetition of the process is a single iteration, and the outcome of each iteration is then the starting point of the next iteration. ...
of a function , so that
The lower limit of the sum, , was chosen so that all terms of the series are positive. Notably, these series provide examples of infinite sums that converge or diverge arbitrarily slowly. For instance, in the case of and , the partial sum exceeds 10 only after (a googolplex
A googolplex is the number 10, or equivalently, 10 or 1010,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 . Written out in ordinary decimal notation, it is 1 fol ...
) terms; yet the series diverges nevertheless.
Schlömilch's generalization
A generalization of the condensation test was given byOskar Schlomilch Oskar may refer to:
* oskar (gene), the Drosophila gene
* Oskar (given name) Oscar or Oskar is a masculine given name of Irish origin.
Etymology
The name is derived from two elements in Irish: the first, ''os'', means "deer"; the second element, ' ...
.Elijah Liflyand, Sergey Tikhonov, & Maria Zeltse (2012Extending tests for convergence of number series
page 7/28 via
Brandeis University
, mottoeng = "Truth even unto its innermost parts"
, established =
, type = Private research university
, accreditation = NECHE
, president = Ronald D. Liebowitz
, p ...
Let be a strictly increasing sequence of positive integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the languag ...
s such that the ratio of successive differences is bounded: there is a positive real number , for which
Then, provided that meets the same preconditions as in Cauchy's convergence test
The Cauchy convergence test is a method used to test infinite series for convergence. It relies on bounding sums of terms in the series. This convergence criterion is named after Augustin-Louis Cauchy who published it in his textbook Cours d'Analy ...
, the convergence of the series is equivalent to the convergence of
Taking so that , the Cauchy condensation test emerges as a special case.
References
* Bonar, Khoury (2006). ''Real Infinite Series''. Mathematical Association of America. .External links
Cauchy condensation test proof
{{Calculus topics Augustin-Louis Cauchy Convergence tests