Cubic Harmonic

In fields like computational chemistry and solid-state and condensed matter physics the so-called atomic orbitals, or spin-orbitals, as they appear in textbooks

on quantum physics, are often partially replaced by cubic harmonics for a number of reasons. These harmonics are usually named tesseral harmonics in the field of condensed matter physics in which the name kubic harmonics rather refers to the irreducible representations in the cubic point-group.

Introduction

The $2l+1$ hydrogen-like atomic orbitals with principal quantum number $n$ and angular momentum quantum number $l$ are often expressed as

:$\psi_(\mathbf) = R_(r) Y_l^m(\theta,\varphi)$

in which the $R_(r)$ is the radial part of the wave function and $Y_l^m(\theta,\varphi)$ is the angular dependent part. The $Y_l^m(\theta,\varphi)$ are the spherical harmonics, which are solutions of the angular momentum operator. The spherical harmonics are representations of functions of the full rotation group SO(3)
with rotational symmetry. In many fields of physics and chemistry these spherical harmonics are replaced by cubic harmonics because the rotational symmetry of the atom and its environment are distorted or because cubic harmonics offer computational benefits.

Symmetry and coordinate system

In many cases, especially in chemistry and solid-state and condensed-matter physics, the system under investigation doesn't have rotational symmetry. Often it has some kind of lower symmetry, with a special point group representation, or it has no spatial symmetry at all. Biological and biochemical systems, like amino acids and enzymes often belong to low molecular symmetry point groups. The solid crystals of the elements often belong to the space groups and point groups with high symmetry. (Cubic harmonics representations are often listed and referenced in point group tables.) The system has at least a fixed orientation in three-dimensional Euclidean space. Therefore, the coordinate system that is used in such cases is most often a Cartesian coordinate system instead of a spherical coordinate system. In a Cartesian coordinate system the atomic orbitals are often expressed as

:$\psi_(\mathbf) = R_(r) X_(\mathbf)$

with the cubic harmonics,


$X_(\mathbf)$, as a basis set. LCAO and MO calculations in computational chemistry or tight binding calculations in solid-state physics use cubic harmonics as an atomic orbital basis. The indices ''lc'' are denoting some kind of Cartesian representation.

Basis transformations

For the representations of the spherical harmonics a spherical coordinate system is chosen with a principal axis in the z-direction. For the cubic harmonics this axis is also the most convenient choice. For states of higher angular momentum quantum number $l$ and a higher dimension of $l(l+1)$ the number of possible rotations or basis transformations in Hilbert space grows and so does the number of possible orthogonal representations that can be constructed on the basis of the $l(l+1)$-dimensional spherical harmonics basis set. There is more freedom to choose a representation that fits the point group symmetry of the problem. The cubic representations that are listed in the table are a result of the transformations, which are 45° 2D rotations and a 90° rotation to the real axis if necessary, like

:$X_(\mathbf) = Y_l^0$
:$X_(\mathbf) = \frac\left(Y_l^m - Y_l^\right)$
:$X_(\mathbf) = \frac\left(Y_l^m + Y_l^\right)$

A substantial number of the spherical harmonics are listed in the Table of spherical harmonics.

Computational benefits

First of all, the cubic harmonics are ''real functions'', while spherical harmonics are ''complex functions''. The complex numbers are two-dimensional with a real part and an imaginary part. Complex numbers offer very handsome and effective tools to tackle mathematical problems analytically but they are not very effective when they are used for numerical calculations. Skipping the imaginary part saves half the calculational effort in summations, a factor of four in multiplications and often factors of eight or even more when it comes to computations involving matrices.

The cubic harmonics often fit the symmetry of the potential or surrounding of an atom. A common surrounding of atoms in solids and chemical complexes is an octahedral surrounding with an octahedral cubic point group symmetry. The representations of the cubic harmonics often have a high symmetry and multiplicity so operations like integrations can be reduced to a limited, or irreducible, part of the domain of the function that has to be evaluated. A problem with the 48-fold octahedral O_h symmetry can be calculated much faster if one limits a calculation, like an integration, to the irreducible part of the domain of the function.

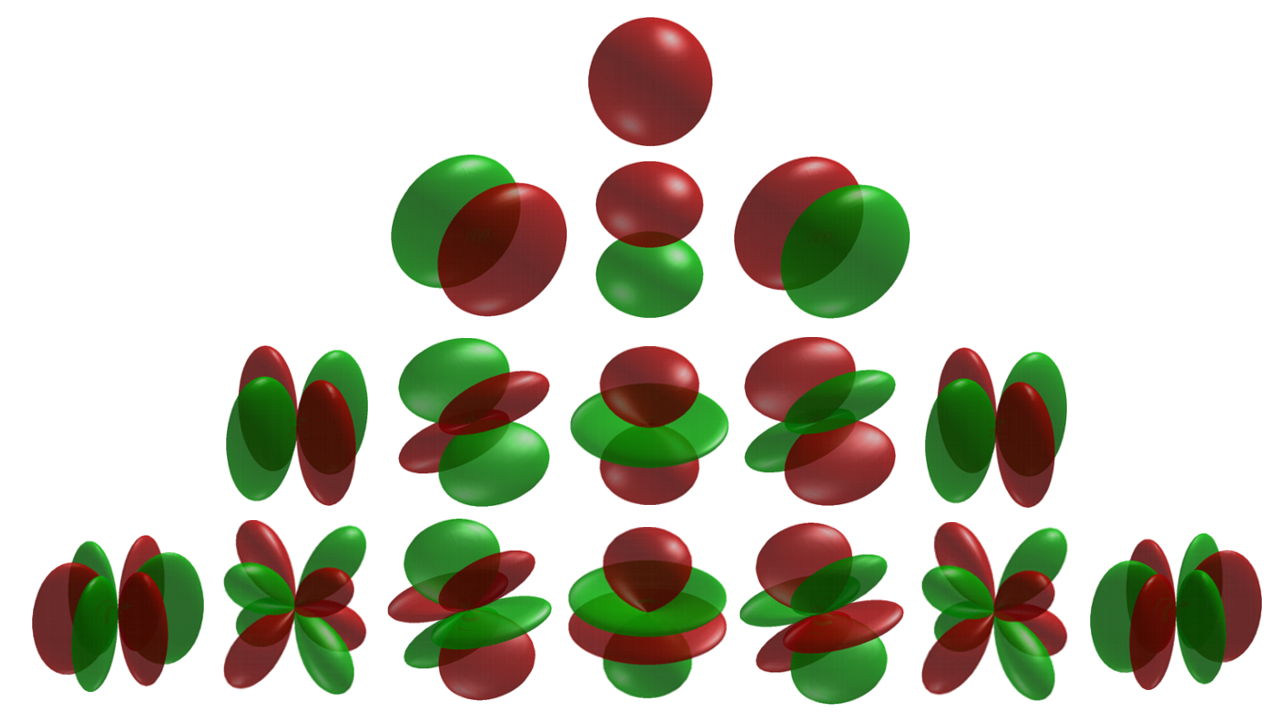
Table of cubic harmonics

The s-orbitals

The s-orbitals only have a radial part.

:$\psi_(\mathbf) = R_(r) Y_0^0$
:$s = X_ = Y_0^0 = \frac$

The p-orbitals

The three p-orbitals are atomic orbitals with an angular momentum quantum number ℓ = 1. The cubic harmonic expression of the p-orbitals

:$p_z = N_1^c \frac = Y_1^0$
:$p_x = N_1^c \frac = \frac \left(Y_1^-Y_1^1\right)$
:$p_y = N_1^c \frac = \frac \left(Y_1^+Y_1^1\right)$
with
:$N_1^c = \left(\frac\right)^$

The d-orbitals

The five d-orbitals are atomic orbitals with an angular momentum quantum number ℓ = 2. The angular part of the d-orbitals are often expressed like

:$\psi_(\mathbf) = R_(r) X_(\mathbf)$

The angular part of the d-orbitals are the cubic harmonics $X_(\mathbf)$

:$d_ = N_2^c \frac = Y_2^0$
:$d_ = N_2^c \frac = \frac \left(Y_2^-Y_2^1\right)$
:$d_ = N_2^c \frac = \frac \left(Y_2^+Y_2^1\right)$
:$d_ = N_2^c \frac = \frac \left(Y_2^-Y_2^2\right)$
:$d_ = N_2^c \frac = \frac \left(Y_2^+Y_2^2\right)$
with
:$N_2^c = \left(\frac\right)^$

The f-orbitals

The seven f-orbitals are atomic orbitals with an angular momentum quantum number ℓ = 3. often expressed like

:$\psi_(\mathbf) = R_(r) X_(\mathbf)$

The angular part of the f-orbitals are the cubic harmonics $X_(\mathbf)$. In many cases different linear combinations of spherical harmonics are chosen to construct a cubic f-orbital basis set.

:$f_ = N_3^c \frac = Y_3^0$
:$f_ = N_3^c \frac = \frac\left(Y_3^-Y_3^1\right)$
:$f_ = N_3^c \frac = \frac\left(Y_3^+Y_3^1\right)$
:$f_ = N_3^c \frac = \frac\left(Y_3^-Y_3^2\right)$
:$f_ = N_3^c \frac = \frac\left(Y_3^+Y_3^2\right)$
:$f_ = N_3^c \frac = \frac\left(Y_3^-Y_3^3\right)$
:$f_ = N_3^c \frac = \frac\left(Y_3^+Y_3^3\right)$
with
:$N_3^c = \left(\frac\right)^$

See also

* Atomic orbitals
* Atomic physics
* Spherical harmonics
* Spherical coordinate system
* Cartesian coordinate system
* Euclidean space
* Hilbert space
* Basis set (chemistry)
* Basis (linear algebra)
* Coordinate vector
* LCAO method
* Tight binding method

References

{{atomic models

Molecular physics
Quantum chemistry
Electronic structure methods
Physical chemistry
Euclidean symmetries