Costas Loop on:
[Wikipedia]
[Google]
[Amazon]
A Costas loop is a
 In the classical implementation of a Costas loop, a local
In the classical implementation of a Costas loop, a local
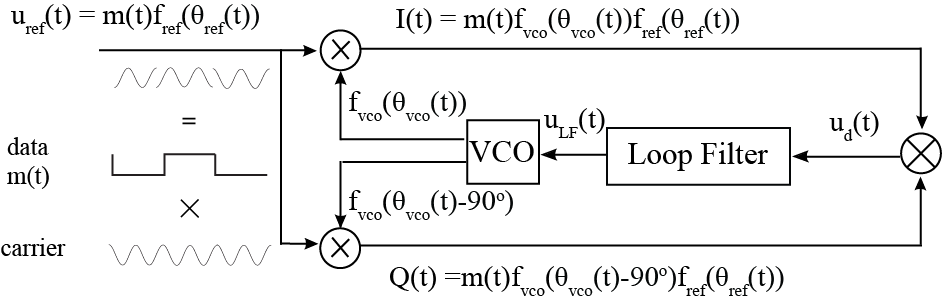 In the simplest case . Therefore, does not affect the input of the noise-reduction filter.
The carrier and
In the simplest case . Therefore, does not affect the input of the noise-reduction filter.
The carrier and

 In the simplest case, when
:
The standard engineering assumption is that the filter removes the upper sideband frequency from the input but leaves the lower sideband without change. Thus it is assumed that the VCO input is This makes a Costas loop equivalent to a
In the simplest case, when
:
The standard engineering assumption is that the filter removes the upper sideband frequency from the input but leaves the lower sideband without change. Thus it is assumed that the VCO input is This makes a Costas loop equivalent to a
 The input
The input
phase-locked loop
A phase-locked loop or phase lock loop (PLL) is a control system that generates an output signal whose phase is related to the phase of an input signal. There are several different types; the simplest is an electronic circuit consisting of a ...
(PLL) based circuit which is used for carrier frequency recovery from suppressed-carrier modulation
In electronics and telecommunications, modulation is the process of varying one or more properties of a periodic waveform, called the '' carrier signal'', with a separate signal called the ''modulation signal'' that typically contains informat ...
signals (e.g. double- sideband suppressed carrier signals) and phase modulation signals (e.g. BPSK
Phase-shift keying (PSK) is a digital modulation process which conveys data by changing (modulating) the phase of a constant frequency reference signal (the carrier wave). The modulation is accomplished by varying the sine and cosine inputs at ...
, QPSK
Phase-shift keying (PSK) is a digital modulation process which conveys data by changing (modulating) the phase of a constant frequency reference signal (the carrier wave). The modulation is accomplished by varying the sine and cosine inputs at ...
). It was invented by John P. Costas at General Electric
General Electric Company (GE) is an American multinational conglomerate founded in 1892, and incorporated in New York state and headquartered in Boston. The company operated in sectors including healthcare, aviation, power, renewable energ ...
in the 1950s. Its invention was described as having had "a profound effect on modern digital communications".
The primary application of Costas loops is in wireless receivers. Its advantage over other PLL-based detectors is that at small deviations the Costas loop error voltage is as compared to . This translates to double the sensitivity and also makes the Costas loop uniquely suited for tracking Doppler-shifted
The Doppler effect or Doppler shift (or simply Doppler, when in context) is the change in frequency of a wave in relation to an observer who is moving relative to the wave source. It is named after the Austrian physicist Christian Doppler, who d ...
carriers, especially in OFDM
In telecommunications, orthogonal frequency-division multiplexing (OFDM) is a type of digital transmission and a method of encoding digital data on multiple carrier frequencies. OFDM has developed into a popular scheme for wideband digital comm ...
and GPS receivers.
Classical implementation
voltage-controlled oscillator
A microwave (12–18GHz) voltage-controlled oscillator
A voltage-controlled oscillator (VCO) is an electronic oscillator whose oscillation frequency is controlled by a voltage input. The applied input voltage determines the instantaneous oscillat ...
(VCO) provides quadrature outputs, one to each of two phase detector
A phase detector or phase comparator is a frequency mixer, analog multiplier or logic circuit that generates a signal which represents the difference in phase between two signal inputs.
The phase detector is an essential element of the phase- ...
s, ''e.g.'', product detectors. The same phase of the input signal
In signal processing, a signal is a function that conveys information about a phenomenon. Any quantity that can vary over space or time can be used as a signal to share messages between observers. The '' IEEE Transactions on Signal Processing' ...
is also applied to both phase detectors, and the output of each phase detector
A phase detector or phase comparator is a frequency mixer, analog multiplier or logic circuit that generates a signal which represents the difference in phase between two signal inputs.
The phase detector is an essential element of the phase- ...
is passed through a low-pass filter
A low-pass filter is a filter that passes signals with a frequency lower than a selected cutoff frequency and attenuates signals with frequencies higher than the cutoff frequency. The exact frequency response of the filter depends on the filt ...
. The outputs of these low-pass filters are inputs to another phase detector, the output of which passes through a noise-reduction filter before being used to control the voltage-controlled oscillator. The overall loop response is controlled by the two individual low-pass filters that precede the third phase detector, while the third low-pass filter serves a trivial role in terms of gain and phase margin.
The above figure of a Costas loop is drawn under the "locked" state, where the VCO frequency and the incoming carrier frequency have become the same due to the Costas loop process. The figure does not represent the "unlocked" state.
Mathematical models
In the time domain
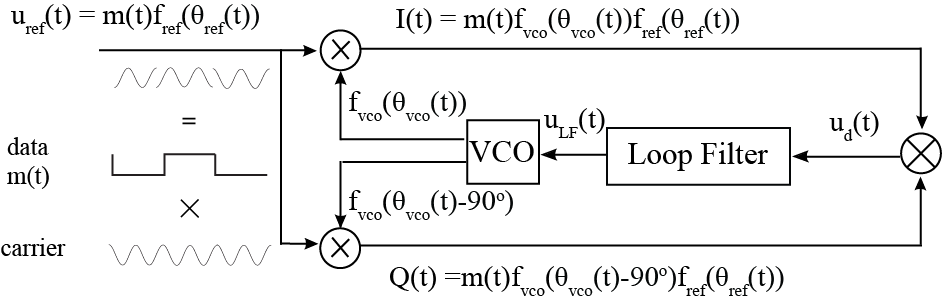 In the simplest case . Therefore, does not affect the input of the noise-reduction filter.
The carrier and
In the simplest case . Therefore, does not affect the input of the noise-reduction filter.
The carrier and voltage-controlled oscillator
A microwave (12–18GHz) voltage-controlled oscillator
A voltage-controlled oscillator (VCO) is an electronic oscillator whose oscillation frequency is controlled by a voltage input. The applied input voltage determines the instantaneous oscillat ...
(VCO) signals are periodic oscillations with high-frequencies .
The block is an analog multiplier.
A linear filter
Linear filters process time-varying input signals to produce output signals, subject to the constraint of linearity. In most cases these linear filters are also time invariant (or shift invariant) in which case they can be analyzed exactly using ...
can be described mathematically by a system of linear differential equations:
:
where is a constant matrix, is a state vector of the filter, and are constant vectors.
The model of a VCO is usually assumed to be linear:
:
where is the free-running frequency of the VCO and is the VCO gain factor. Similarly, it is possible to consider various nonlinear models of VCO.
Suppose that the frequency of the master generator is constant
Equation of VCO and equation of filter yield
:
The system is non-autonomous and rather tricky for investigation.
In the phase-frequency domain

phase-locked loop
A phase-locked loop or phase lock loop (PLL) is a control system that generates an output signal whose phase is related to the phase of an input signal. There are several different types; the simplest is an electronic circuit consisting of a ...
with phase detector characteristic A phase detector characteristic is a function of phase difference describing the output of the phase detector.
For the analysis of Phase detector it is usually considered the models
of PD in signal (time) domain and phase-frequency domain.
In this ...
corresponding to the particular waveforms and of the input and VCO signals. It can be proved that filter outputs in the time and phase-frequency domains are almost equal.
Thus it is possible to study the simpler autonomous system Autonomous system may refer to:
* Autonomous system (Internet), a collection of IP networks and routers under the control of one entity
* Autonomous system (mathematics), a system of ordinary differential equations which does not depend on the inde ...
of differential equations
:.
The Krylov–Bogoliubov averaging method allows one to prove that solutions of non-autonomous and autonomous equations are close under some assumptions.
Thus, the Costas loop block diagram in the time domain can be asymptotically changed to the block diagram on the level of phase-frequency relations.
The transition to the analysis of an autonomous dynamical model of the Costas loop (in place of the non-autonomous one) allows one to overcome the difficulties related to modeling the Costas loop in the time domain, where one has to simultaneously observe a very fast time scale of the input signals and slow time scale of signal's phase. This idea makes it possible to calculate core performance characteristics - hold-in, pull-in, and lock-in ranges.
Frequency acquisition
The classical Costas loop will work towards making the phase difference between the carrier and the VCO become a small, ideally zero, value. The small phase difference implies that frequency lock has been achieved.QPSK Costas loop
The classical Costas loop can be adapted toQPSK
Phase-shift keying (PSK) is a digital modulation process which conveys data by changing (modulating) the phase of a constant frequency reference signal (the carrier wave). The modulation is accomplished by varying the sine and cosine inputs at ...
modulation for higher data rates.
 The input
The input QPSK
Phase-shift keying (PSK) is a digital modulation process which conveys data by changing (modulating) the phase of a constant frequency reference signal (the carrier wave). The modulation is accomplished by varying the sine and cosine inputs at ...
signal is as follows
:
Inputs of low-pass filters LPF1 and LPF2 are
:
After synchronization,
the outputs of LPF1 and LPF2 are used to get demodulated data ( and ). To adjust the frequency of the VCO to the reference frequency, signals and are limited and cross-multiplied:
:
Then the signal is filtered by the loop filter and forms the tuning signal for the VCO , similar to BPSK Costas loop. Thus, QPSK Costas can be described
by a system of ordinary differential equations
In mathematics, an ordinary differential equation (ODE) is a differential equation whose unknown(s) consists of one (or more) function(s) of one variable and involves the derivatives of those functions. The term ''ordinary'' is used in contras ...
:
:
Here are parameters of LPF1 and LPF2 and are parameters of the loop filter.
References
* {{FS1037C Electronic oscillators Communication circuits