constant sheaf

In mathematics, the constant sheaf on a topological space $X$ associated to a set $A$ is a sheaf of sets on $X$ whose stalks are all equal to $A$. It is denoted by $\underline$ or $A_X$. The constant presheaf with value $A$ is the presheaf that assigns to each open subset of $X$ the value $A$, and all of whose restriction maps are the identity map $A\to A$. The constant sheaf associated to $A$ is the sheafification of the constant presheaf associated to $A$. This sheaf may be identified with the sheaf of locally constant $A$-valued functions on $X$.

In certain cases, the set $A$ may be replaced with an object $A$ in some category $\textbf$ (e.g. when $\textbf$ is the category of abelian groups, or commutative rings).

Constant sheaves of abelian groups appear in particular as coefficients in sheaf cohomology.

Basics

Let $X$ be a topological space, and $A$ a set. The sections of the constant sheaf $\underline$ over an open set $U$ may be interpreted as the continuous functions $U\to A$, where $A$ is given the discrete topology. If $U$ is connected, then these locally constant functions are constant. If $f:X\to\$ is the unique map to the one-point space and $A$ is considered as a sheaf on $\$, then the inverse image $f^A$ is the constant sheaf $\underline$ on $X$. The sheaf space of $\underline$ is the projection map $A$ (where $X\times A\to X$ is given the discrete topology).

A detailed example

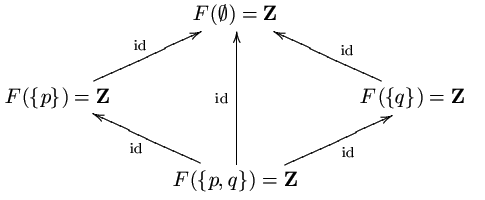
Let $X$ be the topological space consisting of two points $p$ and $q$ with the discrete topology. $X$ has four open sets: $\varnothing, \, \, \$. The five non-trivial inclusions of the open sets of $X$ are shown in the chart.

A presheaf on $X$ chooses a set for each of the four open sets of $X$ and a restriction map for each of the inclusions (with identity map for $U\subset U$). The constant presheaf with value $\textbf$, denoted $F$, is the presheaf where all four sets are $\textbf$, the integers, and all restriction maps are the identity. $F$ is a functor on the diagram of inclusions (a presheaf), because it is constant. It satisfies the gluing axiom, but is not a sheaf because it fails the local identity axiom on the empty set. This is because the empty set is covered by the empty family of sets, $\varnothing = \bigcup\nolimits_ U$, and vacuously, any two sections in $F(\varnothing)$ are equal when restricted to any set in the empty family $\$. The local identity axiom would therefore imply that any two sections in $F(\varnothing)$ are equal, which is false.

To modify this into a presheaf $G$ that satisfies the local identity axiom, let $G(\varnothing)=0$, a one-element set, and give $G$ the value $\textbf$ on all non-empty sets. For each inclusion of open sets, let the restriction be the unique map to 0 if the smaller set is empty, or the identity map otherwise. Note that $G(\varnothing)=0$ is forced by the local identity axiom.

Now $G$ is a separated presheaf (satisfies local identity), but unlike $F$ it fails the gluing axiom. Indeed, $\$ is disconnected, covered by non-intersecting open sets $\$ and $\$. Choose distinct sections $m\neq n$ in $\mathbf Z$ over $\$ and $\$ respectively. Because $m$ and $n$ restrict to the same element 0 over $\varnothing$, the gluing axiom would guarantee the existence of a unique section $s$ on $G(\)$ that restricts to $m$ on $\$ and $n$ on $\$; but the restriction maps are the identity, giving $m = s = n$, which is false. Intuitively, $G(\)$ is too small to carry information about both connected components $\$ and $\$.

Modifying further to satisfy the gluing axiom, let

$H(\) = \mathrm(\,\mathbf)\cong \Z\times\Z$,

the $\mathbf Z$-valued functions on $\$, and define the restriction maps of $H$ to be natural restriction of functions to $\$ and $\$, with the zero map restricting to $\varnothing$. Then $H$ is a sheaf, called the constant sheaf on $X$ with value $\textbf$. Since all restriction maps are ring homomorphisms, $H$ is a sheaf of commutative rings.

See also

* Locally constant sheaf

References

*Section II.1 of
*Section 2.4.6 of

{{DEFAULTSORT:Constant Sheaf
Sheaf theory