Clothoid Loop on:
[Wikipedia]
[Google]
[Amazon]
 An Euler spiral is a curve whose
An Euler spiral is a curve whose
"The Euler spiral: a mathematical history."
Rapp. tech (2008). The behavior of Fresnel integrals can be illustrated by an Euler spiral, a connection first made by
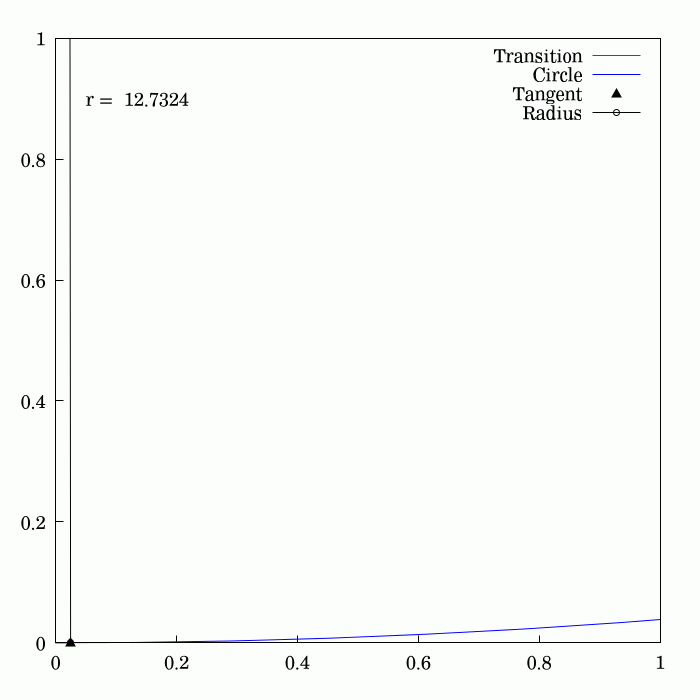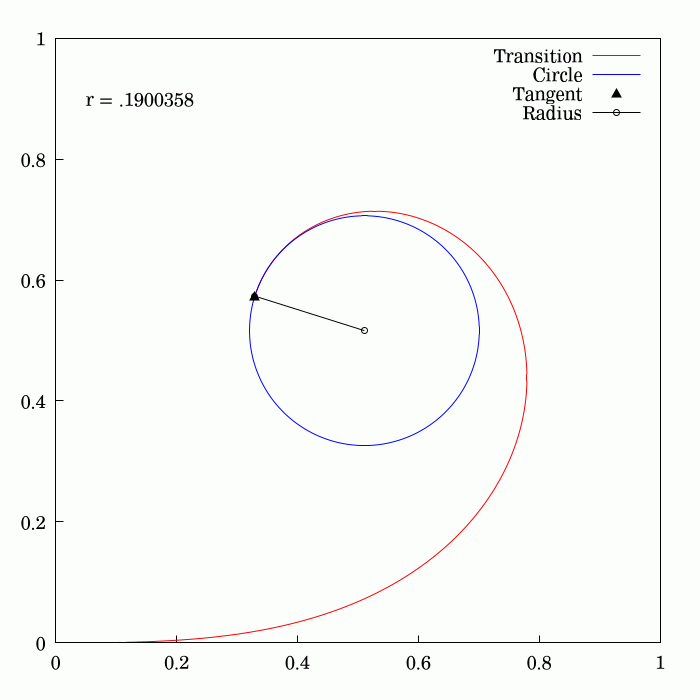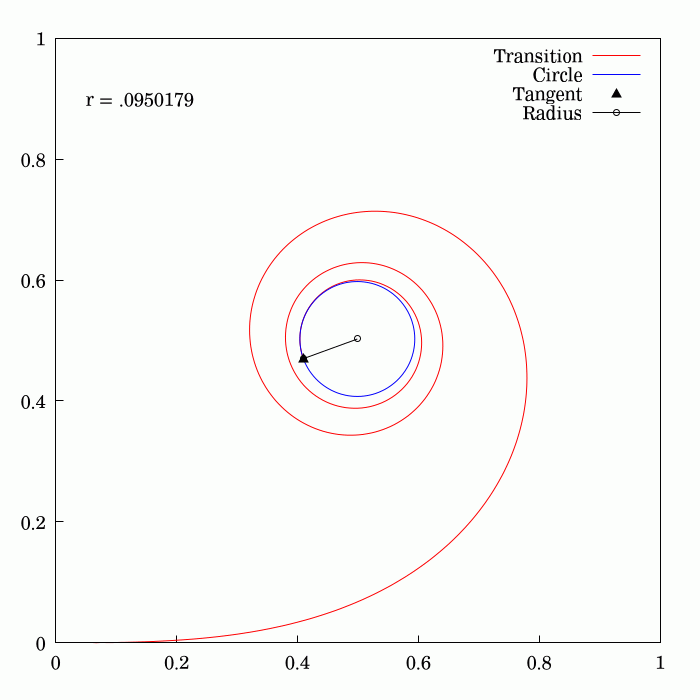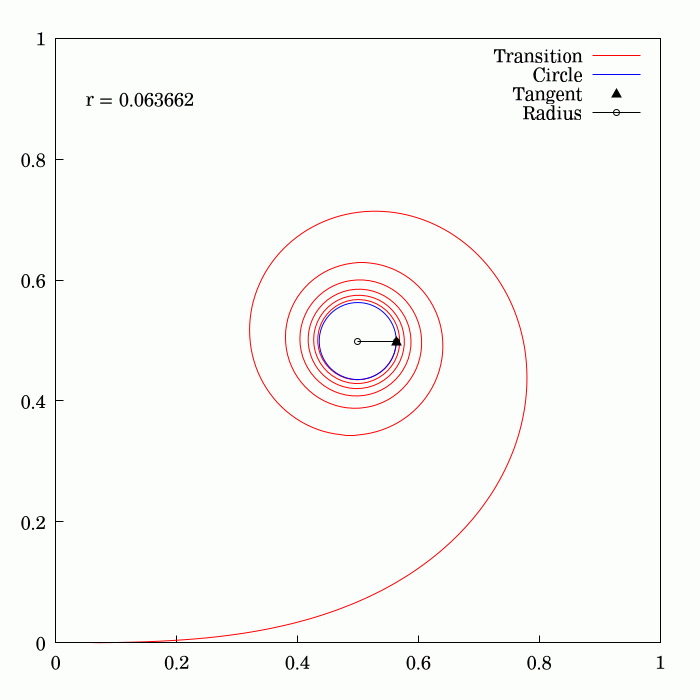 To travel along a circular path, an object needs to be subject to a
To travel along a circular path, an object needs to be subject to a
The Cornu spiral
''Hyperphysics'' (2002) ''(Uses πt²/2 instead of t².)'' * Milton Abramowitz and Irene A. Stegun, eds. '' Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables.'' New York: Dover, 1972.
(See Chapter 7)
' *
Interactive example with JSXGraph
{{DEFAULTSORT:Euler Spiral Transportation engineering Calculus Plane curves Spirals
curvature
In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or su ...
changes linearly with its curve length (the curvature of a circular curve is equal to the reciprocal of the radius). This curve is also referred to as a clothoid or Cornu spiral.Levien, Raph"The Euler spiral: a mathematical history."
Rapp. tech (2008). The behavior of Fresnel integrals can be illustrated by an Euler spiral, a connection first made by
Marie Alfred Cornu
Marie Alfred Cornu (; 6 March 1841 – 12 April 1902) was a French physicist and professor of École polytechnique. The French generally refer to him as Alfred Cornu. The Cornu spiral, a graphical device for the computation of light intensities ...
in 1874. Euler's spiral is a type of superspiral that has the property of a monotonic curvature function.
The Euler spiral has applications to diffraction
Diffraction is the deviation of waves from straight-line propagation without any change in their energy due to an obstacle or through an aperture. The diffracting object or aperture effectively becomes a secondary source of the Wave propagation ...
computations. They are also widely used in railway
Rail transport (also known as train transport) is a means of transport using wheeled vehicles running in railway track, tracks, which usually consist of two parallel steel railway track, rails. Rail transport is one of the two primary means of ...
and highway engineering
Highway engineering (also known as roadway engineering and street engineering) is a professional engineering discipline branching from the civil engineering subdiscipline of transportation engineering that involves the planning, design, construct ...
to design transition curves between straight and curved sections of railways or roads. A similar application is also found in photonic integrated circuit
A photonic integrated circuit (PIC) or integrated optical circuit is a microchip containing two or more photonic components that form a functioning circuit. This technology detects, generates, transports, and processes light. Photonic integrated ci ...
s. The principle of linear variation of the curvature of the transition curve between a tangent and a circular curve defines the geometry of the Euler spiral:
*Its curvature begins with zero at the straight section (the tangent) and increases linearly with its curve length.
*Where the Euler spiral meets the circular curve, its curvature becomes equal to that of the latter.
History
The spiral has multiple names reflecting its discovery and application in multiple fields. The three major arenas were elastic springs ("Euler spiral", 1744), graphical computations in light diffraction ("Cornu spiral", 1874), and railway transitions ("the railway transition spiral", 1890).Leonhard Euler
Leonhard Euler ( ; ; ; 15 April 170718 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential ...
's work on the spiral came after James Bernoulli posed a problem in the theory of elasticity: what shape must a pre-curved wire spring be in such that, when flattened by pressing on the free end, it becomes a straight line? Euler established the properties of the spiral in 1744, noting at that time that the curve must have two limits, points that the curve wraps around and around but never reaches. Thirty-eight years later, in 1781, he reported his discovery of the formula for the limit (by "happy chance").
Augustin Fresnel
Augustin-Jean Fresnel (10 May 1788 – 14 July 1827) was a French civil engineer and physicist whose research in optics led to the almost unanimous acceptance of the wave theory of light, excluding any remnant of Isaac Newton, Newton's c ...
, working in 1818 on the diffraction
Diffraction is the deviation of waves from straight-line propagation without any change in their energy due to an obstacle or through an aperture. The diffracting object or aperture effectively becomes a secondary source of the Wave propagation ...
of light, developed the Fresnel integral
250px,
Plots of and . The maximum of is about . If the integrands of and were defined using instead of , then the image would be scaled vertically and horizontally (see below).
The Fresnel integrals and are two transcendental functions n ...
that defines the same spiral. He was unaware of Euler's integrals or the connection to the theory of elasticity. In 1874, Alfred Marie Cornu showed that diffraction intensity could be read off a graph of the spiral by squaring the distance between two points on the graph. In his biographical sketch of Cornu, Henri Poincaré
Jules Henri Poincaré (, ; ; 29 April 185417 July 1912) was a French mathematician, Theoretical physics, theoretical physicist, engineer, and philosophy of science, philosopher of science. He is often described as a polymath, and in mathemati ...
praised the advantages of the "spiral of Cornu" over the "unpleasant multitude of hairy integral formulas". Ernesto Cesàro
Ernesto Cesàro (12 March 1859 – 12 September 1906) was an Italian mathematician who worked in the field of differential geometry. He wrote a book, ''Lezioni di geometria intrinseca'' (Naples, 1890), on this topic, in which he also describes ...
chose to name the same curve "clothoid" after Clotho
Clotho (; ) or Klotho, is a mythological figure. She was one of the Three Fates or Moirai. In ancient Greek mythology, she spins the thread of human life, her sisters draw out ( Lachesis) and cut ( Atropos) the thread. She also made major dec ...
, one of the three Fates
The Fates are a common motif in European polytheism, most frequently represented as a trio of goddesses. The Fates shape the destiny of each human, often expressed in textile metaphors such as spinning fibers into yarn, or weaving threads on a ...
who spin the thread of life in Greek mythology
Greek mythology is the body of myths originally told by the Ancient Greece, ancient Greeks, and a genre of ancient Greek folklore, today absorbed alongside Roman mythology into the broader designation of classical mythology. These stories conc ...
.
The third independent discovery occurred in the 1800s when various railway engineers sought a formula for gradual curvature in track shape. By 1880 Arthur Newell Talbot worked out the integral formulas and their solution, which he called the "railway transition spiral". The connection to Euler's work was not made until 1922.
Unaware of the solution of the geometry by Euler, William Rankine
William John Macquorn Rankine (; 5 July 1820 – 24 December 1872) was a Scottish mathematician and physicist. He was a founding contributor, with Rudolf Clausius and William Thomson (Lord Kelvin), to the science of thermodynamics, particularly ...
cited the cubic curve
In mathematics, a cubic plane curve is a plane algebraic curve defined by a cubic equation
:
applied to homogeneous coordinates for the projective plane; or the inhomogeneous version for the affine space determined by setting in such an eq ...
(a polynomial curve of degree 3), which is an approximation of the Euler spiral for small angular changes in the same way that a parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactl ...
is an approximation to a circular curve.
Applications
Track transition curve
 To travel along a circular path, an object needs to be subject to a
To travel along a circular path, an object needs to be subject to a centripetal acceleration
In mechanics, acceleration is the rate of change of the velocity of an object with respect to time. Acceleration is one of several components of kinematics, the study of motion. Accelerations are vector quantities (in that they have magn ...
(for example: the Moon circles around the Earth because of gravity; a car turns its front wheels inward to generate a centripetal force). If a vehicle traveling on a straight path were to suddenly transition to a tangential circular path, it would require centripetal acceleration suddenly switching at the tangent point from zero to the required value; this would be difficult to achieve (think of a driver instantly moving the steering wheel from straight line to turning position, and the car actually doing it), putting mechanical stress on the vehicle's parts, and causing much discomfort (due to lateral jerk).
On early railroads this instant application of lateral force was not an issue since low speeds and wide-radius curves were employed (lateral forces on the passengers and the lateral sway was small and tolerable). As speeds of rail vehicles increased over the years, it became obvious that an easement is necessary, so that the centripetal acceleration increases smoothly with the traveled distance. Given the expression of centripetal acceleration , the obvious solution is to provide an easement curve whose curvature, , increases linearly with the traveled distance.
Optics
Inoptics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of optical instruments, instruments that use or Photodetector, detect it. Optics usually describes t ...
, the term Cornu spiral is used.
The Cornu spiral can be used to describe a diffraction
Diffraction is the deviation of waves from straight-line propagation without any change in their energy due to an obstacle or through an aperture. The diffracting object or aperture effectively becomes a secondary source of the Wave propagation ...
pattern.
Consider a plane wave with phasor amplitude which is diffracted by a "knife edge" of height above on the plane. Then the diffracted wave field can be expressed as
where is the Fresnel integral
250px,
Plots of and . The maximum of is about . If the integrands of and were defined using instead of , then the image would be scaled vertically and horizontally (see below).
The Fresnel integrals and are two transcendental functions n ...
function, which forms the Cornu spiral on the complex plane.
So, to simplify the calculation of plane wave attenuation as it is diffracted from the knife-edge, one can use the diagram of a Cornu spiral by representing the quantities as the physical distances between the points represented by and for appropriate and . This facilitates a rough computation of the attenuation of the plane wave by the knife edge of height at a location beyond the knife edge.
Integrated optics
Bends with continuously varying radius of curvature following the Euler spiral are also used to reduce losses inphotonic integrated circuit
A photonic integrated circuit (PIC) or integrated optical circuit is a microchip containing two or more photonic components that form a functioning circuit. This technology detects, generates, transports, and processes light. Photonic integrated ci ...
s, either in singlemode waveguides
A waveguide is a structure that guides waves by restricting the transmission of energy to one direction. Common types of waveguides include acoustic waveguides which direct sound, optical waveguides which direct light, and radio-frequency wav ...
, to smoothen the abrupt change of curvature and suppress coupling to radiation modes, or in multimode waveguides, in order to suppress coupling to higher order modes and ensure effective singlemode operation.
A pioneering and very elegant application of the Euler spiral to waveguides had been made as early as 1957, with a hollow metal waveguide
A waveguide is a structure that guides waves by restricting the transmission of energy to one direction. Common types of waveguides include acoustic waveguides which direct sound, optical waveguides which direct light, and radio-frequency w ...
for microwaves. There the idea was to exploit the fact that a straight metal waveguide can be physically bent to naturally take a gradual bend shape resembling an Euler spiral.
Feynman's path integral
In thepath integral formulation
The path integral formulation is a description in quantum mechanics that generalizes the stationary action principle of classical mechanics. It replaces the classical notion of a single, unique classical trajectory for a system with a sum, or ...
of quantum mechanics, the probability amplitude for propagation between two points can be visualized by connecting action
Action may refer to:
* Action (philosophy), something which is done by a person
* Action principles the heart of fundamental physics
* Action (narrative), a literary mode
* Action fiction, a type of genre fiction
* Action game, a genre of video gam ...
phase arrows for each time step between the two points. The arrows spiral around each endpoint forming what is termed a Cornu spiral.
Auto racing
Motorsport author Adam Brouillard has shown the Euler spiral's use in optimizing theracing line
In motorsport, the racing line or simply "the line" is the optimal path around a race course. In most cases, the line makes use of the entire width of the track to lengthen the radius of a turn: entering at the outside edge, touching the "apex"—a ...
during the corner entry portion of a turn.
Typography and digital vector drawing
Raph Levien
Raphael Linus Levien (also known as Raph Levien) is a software developer, a member of the free software developer community, through his creation of the Advogato virtual community and his work with the free software branch of Ghostscript. From 20 ...
has released Spiro as a toolkit for curve design, especially font design, in 2007 under a free licence. This toolkit has been implemented quite quickly afterwards in the font design tool Fontforge
FontForge is a FOSS font editor which supports many common font formats. Developed primarily by George Williams until 2012, FontForge is free software and is distributed under a mix of the GNU General Public License Version 3 and the 3-clause ...
and the digital vector drawing Inkscape
Inkscape is a vector graphics editor. It is used for both artistic and technical illustrations such as cartoons, clip art, logos, typography, diagrams, and flowcharts. It uses vector graphics to allow for sharp printouts and renderings at ...
.
Map projection
Cutting a sphere along a spiral with width and flattening out the resulting shape yields an Euler spiral when tends to the infinity. If the sphere is theglobe
A globe is a spherical Earth, spherical Model#Physical model, model of Earth, of some other astronomical object, celestial body, or of the celestial sphere. Globes serve purposes similar to maps, but, unlike maps, they do not distort the surface ...
, this produces a map projection
In cartography, a map projection is any of a broad set of Transformation (function) , transformations employed to represent the curved two-dimensional Surface (mathematics), surface of a globe on a Plane (mathematics), plane. In a map projection, ...
whose distortion tends to zero as tends to the infinity.
Whisker shapes
Natural shapes of rats'whiskers
Whiskers, also known as vibrissae (; vibrissa; ) are a type of stiff, functional hair used by most therian mammals to sense their environment. These hairs are finely specialised for this purpose, whereas other types of hair are coarser as ta ...
are well approximated by segments of Euler spirals; for a single rat all of the whiskers can be approximated as segments of the same spiral. The two parameters of the Cesàro equation
In geometry, the Cesàro equation of a plane curve is an equation relating the curvature () at a point of the curve to the arc length () from the start of the curve to the given point. It may also be given as an equation relating the radius of curv ...
for an Euler spiral segment might give insight into the keratin
Keratin () is one of a family of structural fibrous proteins also known as ''scleroproteins''. It is the key structural material making up Scale (anatomy), scales, hair, Nail (anatomy), nails, feathers, horn (anatomy), horns, claws, Hoof, hoove ...
ization mechanism of whisker growth.
Formulation
Symbols
Expansion of Fresnel integral
If , which is the case for normalized Euler curve, then the Cartesian coordinates are given by Fresnel integrals (or Euler integrals):Normalization
For a given Euler curve with: or then where The process of obtaining solution of of an Euler spiral can thus be described as: * Map of the original Euler spiral by multiplying with factor to of the normalized Euler spiral; * Find from the Fresnel integrals; and * Map to by scaling up (denormalize) with factor . Note that . In the normalization process, Then Generally the normalization reduces to a small value (less than 1) and results in good converging characteristics of the Fresnel integral manageable with only a few terms (at a price of increasednumerical instability
In the mathematical subfield of numerical analysis, numerical stability is a generally desirable property of numerical algorithms. The precise definition of stability depends on the context: one important context is numerical linear algebra, and a ...
of the calculation, especially for bigger values.).Illustration
Given: Then and We scale down the Euler spiral by , i.e. 100 to normalized Euler spiral that has: and The two angles are the same. This thus confirms that the original and normalized Euler spirals are geometrically similar. The locus of the normalized curve can be determined from Fresnel Integral, while the locus of the original Euler spiral can be obtained by scaling up or denormalizing.Other properties of normalized Euler spirals
Normalized Euler spirals can be expressed as: or expressed aspower series
In mathematics, a power series (in one variable) is an infinite series of the form
\sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots
where ''a_n'' represents the coefficient of the ''n''th term and ''c'' is a co ...
:
The normalized Euler spiral will converge to a single point in the limit as the parameter L approaches infinity, which can be expressed as:
Normalized Euler spirals have the following properties:
and
Note that also means , in agreement with the last mathematical statement.
See also
* List of spiralsReferences
Further reading
* *R. NaveThe Cornu spiral
''Hyperphysics'' (2002) ''(Uses πt²/2 instead of t².)'' * Milton Abramowitz and Irene A. Stegun, eds. '' Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables.'' New York: Dover, 1972.
(See Chapter 7)
' *
External links
*Interactive example with JSXGraph
{{DEFAULTSORT:Euler Spiral Transportation engineering Calculus Plane curves Spirals