Chaos Game on:
[Wikipedia]
[Google]
[Amazon]

 In
In
 If the chaos game is run with a square, no fractal appears and the interior of the square fills evenly with points. However, if restrictions are placed on the choice of vertices, fractals will appear in the square. For example, if the current vertex cannot be chosen in the next iteration, this fractal appears:
If the chaos game is run with a square, no fractal appears and the interior of the square fills evenly with points. However, if restrictions are placed on the choice of vertices, fractals will appear in the square. For example, if the current vertex cannot be chosen in the next iteration, this fractal appears:
 If the current vertex cannot be one place away (anti-clockwise) from the previously chosen vertex, this fractal appears:
If the current vertex cannot be one place away (anti-clockwise) from the previously chosen vertex, this fractal appears:
 If the point is prevented from landing on a particular region of the square, the shape of that region will be reproduced as a fractal in other and apparently unrestricted parts of the square. Here, for example, is the fractal produced when the point cannot jump so as to land on a red Om symbol at the center of the square:
If the point is prevented from landing on a particular region of the square, the shape of that region will be reproduced as a fractal in other and apparently unrestricted parts of the square. Here, for example, is the fractal produced when the point cannot jump so as to land on a red Om symbol at the center of the square:

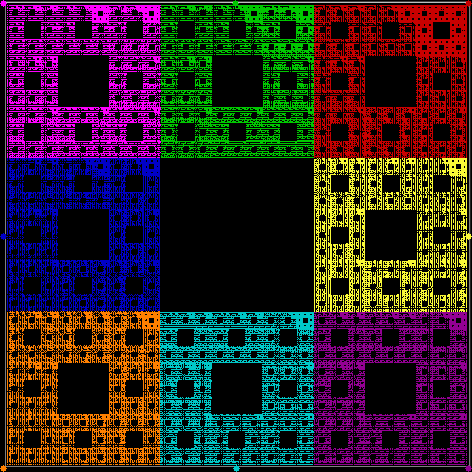
 When the jump is 2/3 and the point can also jump towards the midpoints of the four sides, the chaos game generates the Sierpinski carpet:
When the jump is 2/3 and the point can also jump towards the midpoints of the four sides, the chaos game generates the Sierpinski carpet:
 When the jump is 1/
When the jump is 1/
Simulations
of chaos games made with
Explanation of the chaos game
at beltoforion.de.

 In
In mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, the term chaos game originally referred to a method of creating a fractal
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illu ...
, using a polygon and an initial point selected at random inside it. The fractal is created by iteratively creating a sequence of points, starting with the initial random point, in which each point in the sequence is a given fraction
A fraction (from la, fractus, "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight ...
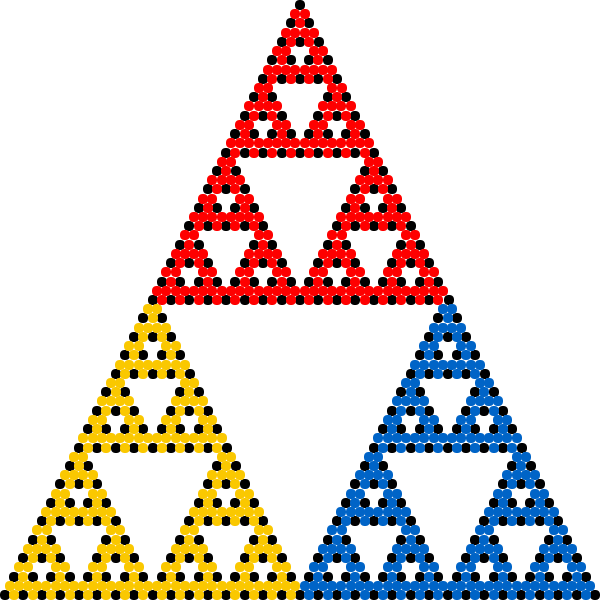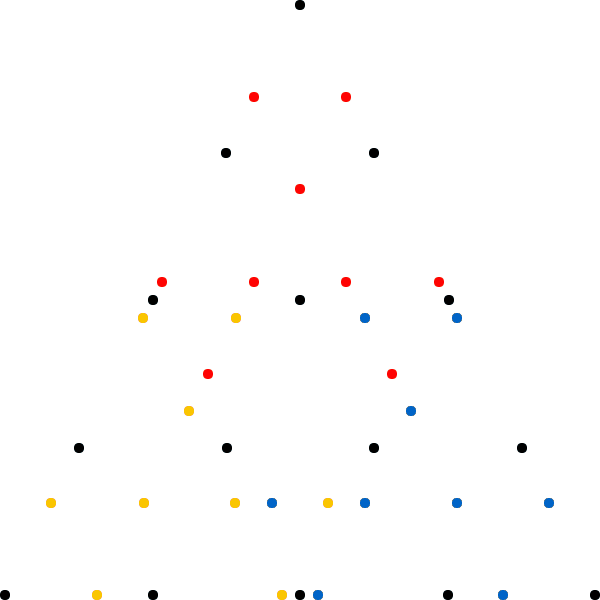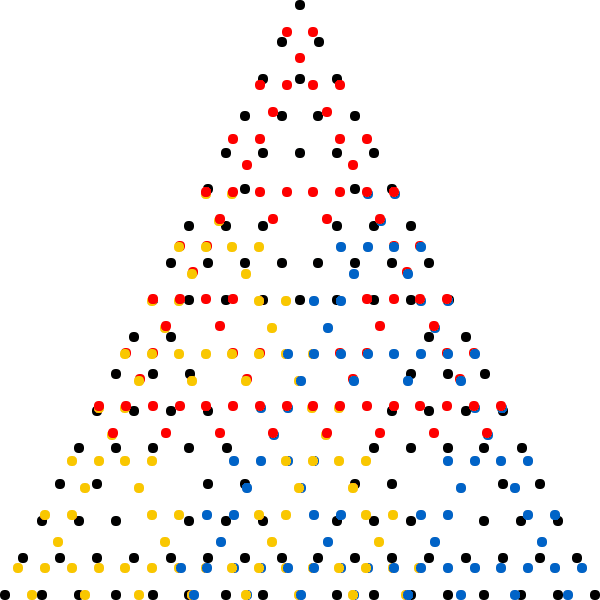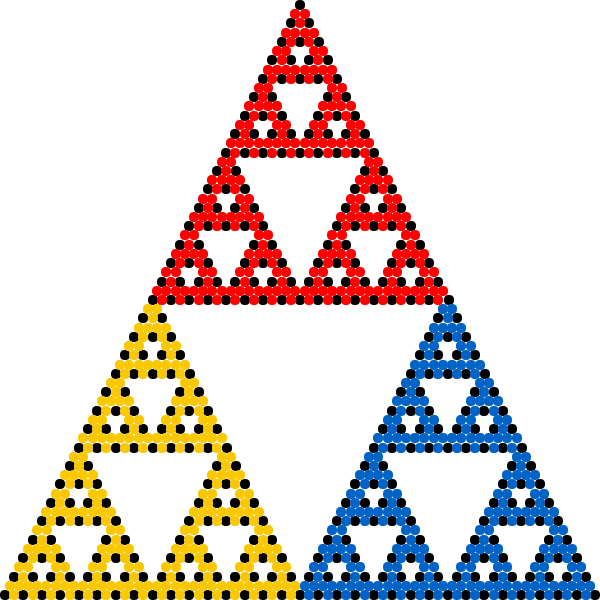
of the distance between the previous point and one of the vertices of the polygon; the vertex is chosen at random in each iteration. Repeating this iterative process a large number of times, selecting the vertex at random on each iteration, and throwing out the first few points in the sequence, will often (but not always) produce a fractal shape. Using a regular triangle and the factor 1/2 will result in the Sierpinski triangle, while creating the proper arrangement with four points and a factor 1/2 will create a display of a "Sierpinski Tetrahedron", the three-dimensional analogue of the Sierpinski triangle. As the number of points is increased to a number N, the arrangement forms a corresponding (N-1)-dimensional Sierpinski Simplex
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. ...
.
The term has been generalized to refer to a method of generating the attractor, or the fixed point, of any iterated function system
In mathematics, iterated function systems (IFSs) are a method of constructing fractals; the resulting fractals are often self-similar. IFS fractals are more related to set theory than fractal geometry. They were introduced in 1981.
IFS fractals, ...
(IFS). Starting with any point x0, successive iterations are formed as xk+1 = fr(xk), where fr is a member of the given IFS randomly selected for each iteration. The iterations converge to the fixed point of the IFS. Whenever x0 belongs to the attractor of the IFS, all iterations xk stay inside the attractor and, with probability 1, form a dense set in the latter.
The "chaos game" method plots points in random order all over the attractor. This is in contrast to other methods of drawing fractals, which test each pixel on the screen to see whether it belongs to the fractal. The general shape of a fractal can be plotted quickly with the "chaos game" method, but it may be difficult to plot some areas of the fractal in detail.
With the aid of the "chaos game" a new fractal can be made and while making the new fractal some parameters can be obtained. These parameters are useful for applications of fractal theory such as classification and identification. The new fractal is self-similar to the original in some important features such as fractal dimension.
Restricted chaos game
 If the chaos game is run with a square, no fractal appears and the interior of the square fills evenly with points. However, if restrictions are placed on the choice of vertices, fractals will appear in the square. For example, if the current vertex cannot be chosen in the next iteration, this fractal appears:
If the chaos game is run with a square, no fractal appears and the interior of the square fills evenly with points. However, if restrictions are placed on the choice of vertices, fractals will appear in the square. For example, if the current vertex cannot be chosen in the next iteration, this fractal appears:
 If the current vertex cannot be one place away (anti-clockwise) from the previously chosen vertex, this fractal appears:
If the current vertex cannot be one place away (anti-clockwise) from the previously chosen vertex, this fractal appears:
 If the point is prevented from landing on a particular region of the square, the shape of that region will be reproduced as a fractal in other and apparently unrestricted parts of the square. Here, for example, is the fractal produced when the point cannot jump so as to land on a red Om symbol at the center of the square:
If the point is prevented from landing on a particular region of the square, the shape of that region will be reproduced as a fractal in other and apparently unrestricted parts of the square. Here, for example, is the fractal produced when the point cannot jump so as to land on a red Om symbol at the center of the square:

Jumps other than 1/2
When the length of the jump towards a vertex or another point is not 1/2, the chaos game generates other fractals, some of them very well-known. For example, when the jump is 2/3 and the point can also jump towards the center of the square, the chaos game generates the Vicsek fractal: When the jump is 2/3 and the point can also jump towards the midpoints of the four sides, the chaos game generates the Sierpinski carpet:
When the jump is 2/3 and the point can also jump towards the midpoints of the four sides, the chaos game generates the Sierpinski carpet:
 When the jump is 1/
When the jump is 1/phi
Phi (; uppercase Φ, lowercase φ or ϕ; grc, ϕεῖ ''pheî'' ; Modern Greek: ''fi'' ) is the 21st letter of the Greek alphabet.
In Archaic and Classical Greek (c. 9th century BC to 4th century BC), it represented an aspirated voiceles ...
and the point is jumping at random towards one or another of the five vertices of a regular pentagon, the chaos game generates a pentagonal n-flake
An ''n''-flake, polyflake, or Sierpinski ''n''-gon, is a fractal constructed starting from an ''n''-gon. This ''n''-gon is replaced by a flake of smaller ''n''-gons, such that the scaled polygons are placed at the vertices, and sometimes in the c ...
:

See also
*Chaos theory
Chaos theory is an interdisciplinary area of scientific study and branch of mathematics focused on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions, and were once thought to have ...
External links
Simulations
of chaos games made with
Scratch
Scratch or scratching may refer to:
Science and technology
* Scratch (programming language), an educational programming language developed by MIT Media Lab
* Scratch space, space on the hard disk drive that is dedicated for only temporary stor ...
.Explanation of the chaos game
at beltoforion.de.
References
{{Fractals, state=collapsed Fractals Chaos theory